一类离散型结核病模型的全局稳定性
2015-09-18李粱晨
陈 辉,李粱晨
(军械工程学院 基础部,石家庄 050003)
一类离散型结核病模型的全局稳定性
陈辉,李粱晨
(军械工程学院 基础部,石家庄050003)
本文研究了一类离散型结核病模型.利用求再生矩阵谱半径的方法,计算得到模型的基本再生数R0.运用差分方程相关理论,证明了模型解的正性和有界性.通过构造适当的Lyapunov函数,证明了R0=1是决定疾病消失或者持续的阈值.当基本再生数R0<1时,无病平衡点是全局渐近稳定的;当基本再生数R0>1时,地方病平衡点是全局渐近稳定的.
结核病;基本再生数;Lyapunov函数;全局渐近稳定
0 引 言
结核病是由结核分枝杆菌感染所引起的一种慢性传染病,对人类的影响已有数千年.现在,全球结核病正持续蔓延,结核病流行趋势也十分严峻.近年来,许多学者从事着结核病方面的研究,考虑到影响结核病发展流行的诸多因素,由此建立了许多数学模型[1-4].
刚刚被结核杆菌感染的结核杆菌携带者进展为活动性结核患者的可能性较大.随着时间的推移,结核杆菌携带者仍然有可能进展成为活动性的结核患者,但是这种可能性比刚刚被感染的时候要小得多.也就是说,结核杆菌携带者进展成为活动性的结核患者的概率随着被感染时间的增加而减小.基于结核病的这个特点,一些学者建立了一系列的动力学模型来研究结核病的传播.文献[5]提出了一类比较简单的SEI结核病模型,将总人口分为3类:易感者(S)、潜伏者(E)和染病者(I).采用双线性发生率βSI,它被分为两部分:一部分pβSI用来描述被结核杆菌感染后很快进展为活动性的结核患者;而(1-p)βSI则用来表示被结核杆菌感染后首先成为潜伏者,经过一段潜伏时间后再进展为活动性的结核患者.但是这个模型并没有考虑结核病的治疗因素,事实上,在全球的大多数地区,结核病是可以被治疗的.基于这个因素,文献[6]提出了一类新的SEIR结核病模型
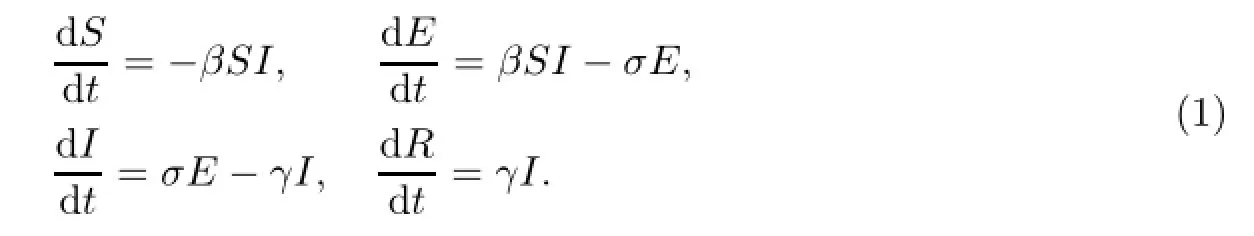
模型(1)即式(1)将总人口分为4类:易感者类(S)、潜伏者类E、染病者类(I)和治愈者类(R).β表示结核病的感染率;σ表示潜伏者E进入感染者I的比例;γ表示结核病患者被治愈的比例.通过构造适当的Lyapunov函数,作者证明了模型(1)的各平衡点是全局渐近稳定的.
然而,模型(1)忽略了人口的出生率和死亡率,这种情况在实际中是不合理的.文献[7-11]也研究了几类结核病模型,考虑了结核病模型中的一些因素,例如人口的动力学因素、可变潜伏期、有疫苗接种、非线性感染率等等.这些学者大都是通过构造连续的微分方程模型进行分析的.然而,通过构造差分方程去研究结核病的文献还不多.事实上,早在1962年,Waaler建立的第一个结核病传染的动力学模型就是一个线性离散模型,这说明离散模型是可以被应用到结核病的研究中的.文献[12]考虑了年龄结构对治疗结核病的影响因素,将不同年龄阶段进行划分,研究了一类离散型SLIT结核病模型,得到了模型平衡点的全局性态.
考虑结核病传播过程中的快慢因素和治疗因素,在前人工作[5-12]的基础上,本文建立了一类离散的SEIT模型
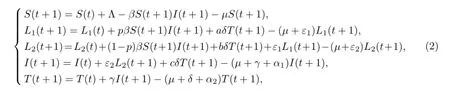
模型(2)即式(2)将总人口分为4类:易感者类(S)、潜伏者类(L1和L2)、染病者类(I)以及治愈者类(T).L1为结核杆菌感染后较慢进展为活动性的结核患者的部分;L2则用来表示被结核杆菌感染后很快进展为结核患者的部分;Λ表示人口的常数输入率;µ表示人口的自然死亡率;β表示结核病的感染率;0<p<1表示易感者被结核杆菌感染后进入L1的比例,1-p表示易感者被结核杆菌感染后进入L2的比例;ε1为较慢部分L1转换为较快部分L2的比率;ε2表示潜伏者中进展较快的部分L2转变为染病者的比例;a,b和c(这里a+b+c=1)表示治愈者分别进入潜伏者中较慢部分L1、潜伏者中较快部分L2以及染病者I的比例,其中0≤c≤1反映了治疗的成功率,c=1说明治疗失败,所有治疗的患者将始终停留在染病者类,c=0说明治疗成功,治愈者全部进入潜伏者类;α1和α2表示染病者在治疗过程中的因病死亡率;γ表示治愈率;δ表示离开治愈者类的比例.为了方便对模型(2)的研究,令
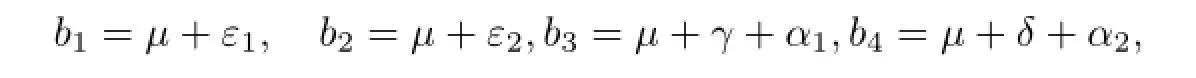
模型(2)的初始条件为
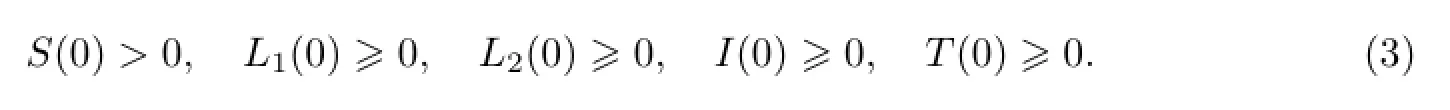
本文的结构是:第1节,利用差分方程的相关理论[3]分析模型(2)的平衡点的存在性;第2节,利用差分方程相关理论证明模型解的正性及有界性;第3节,通过构造适当的Lyapunov函数,利用LaSalle-Lyapunov定理[4],证明无病平衡点以及地方病平衡点是全局渐近稳定的;第4节,通过数值模拟说明理论结果.
1 基本再生数及平衡点
显然,模型(2)总存在无病平衡点
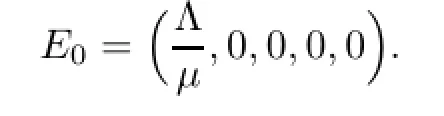
应用文献[13]中计算SEIR模型基本再生数的方法,令X=(L1,L2,I,T,S)T,此时模型(2)可以被表示为
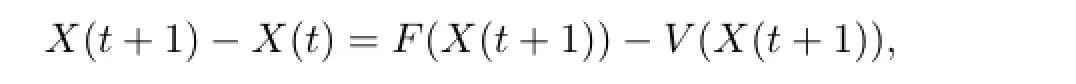
其中,
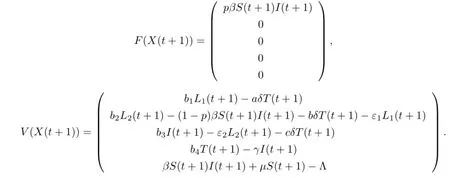
F(X(t+1))和V(X(t+1))在无病平衡点E0处的雅克比矩阵分别为
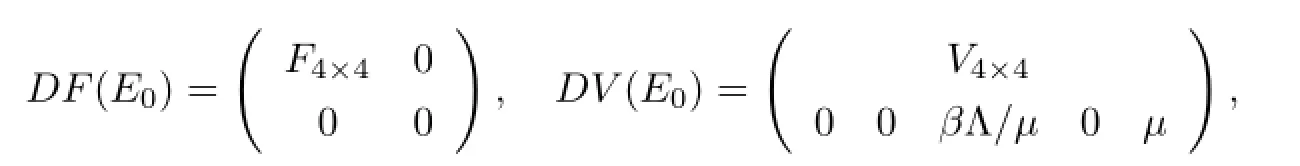
其中
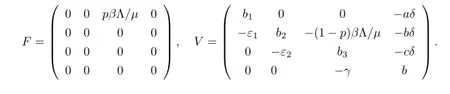
因此,模型(2)的基本再生数为
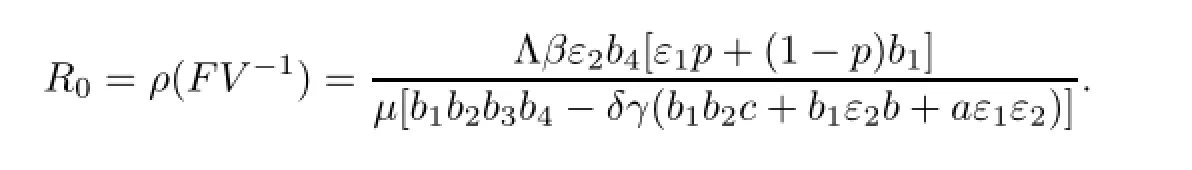
则当R0>1时,模型(2)存在唯一的地方病平衡点其中
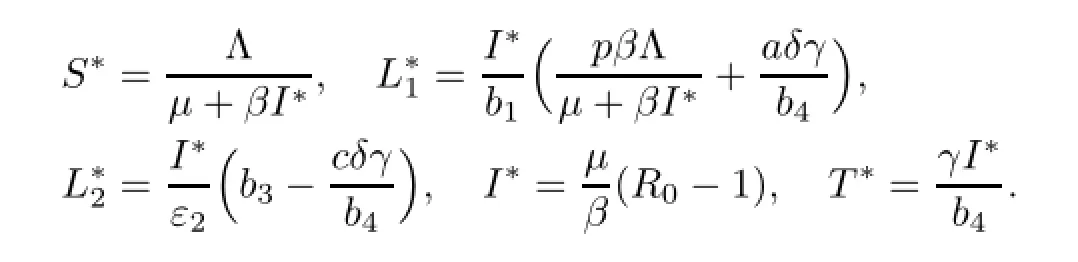
2 解的正性及有界性
引理1满足模型(2)的任意解(S(t),L1(t),L2(t),I(t),T(t))是有界的.
证明令N(t)=S(t)+L1(t)+L2(t)+I(t)+T(t),容易得到
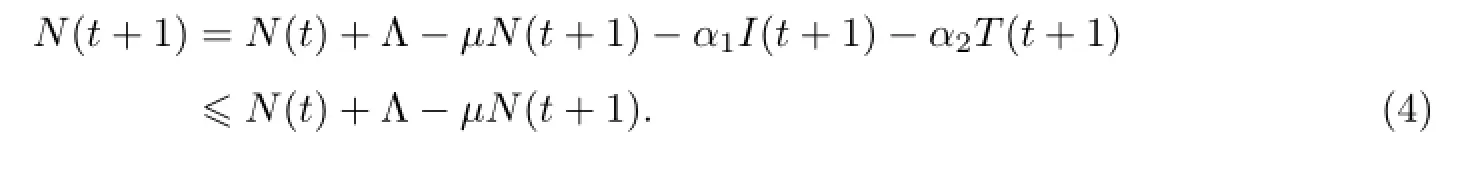
由方程(4)得
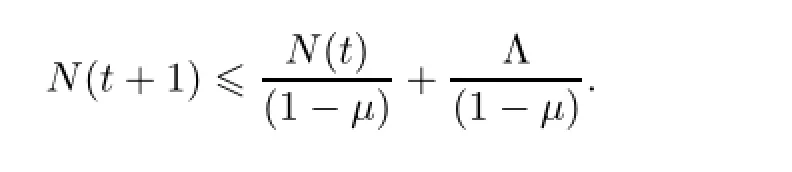
令
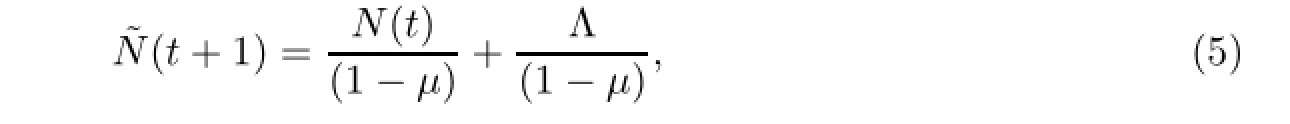
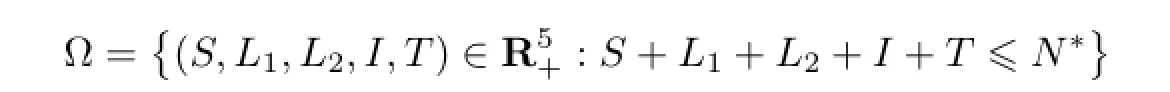
引理2模型(2)中,对于满足初始条件式(3)的任意解{S(t)},{L1(t)},{L2(t)},{I(t)},{T(t)},都有S(t)>0,L1(t)>0,L2(t)>0,I(t)>0,T(t)>0,t∈N+.
证明由模型(2)的第一个方程得
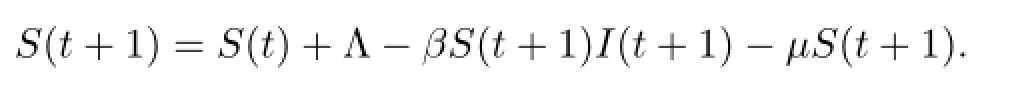
所以
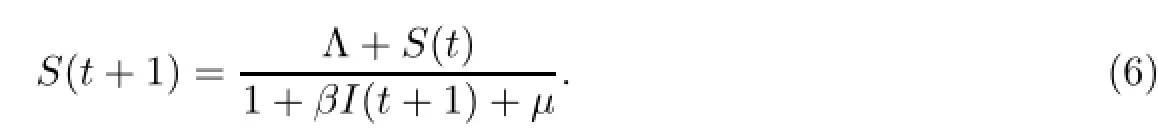
又由模型(2)的第二个方程可得
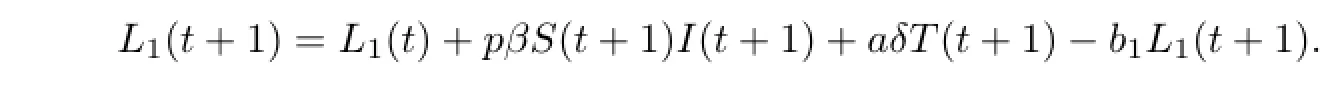
因此
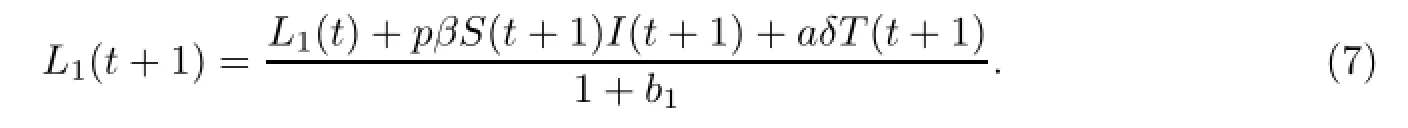
再由模型(2)的第三个方程可得
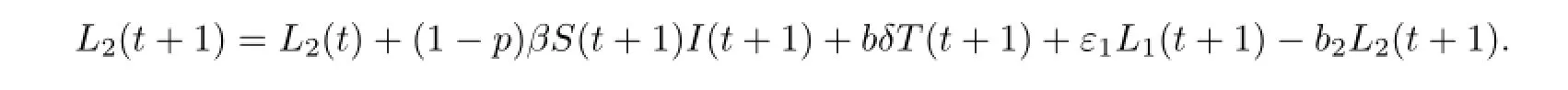
于是
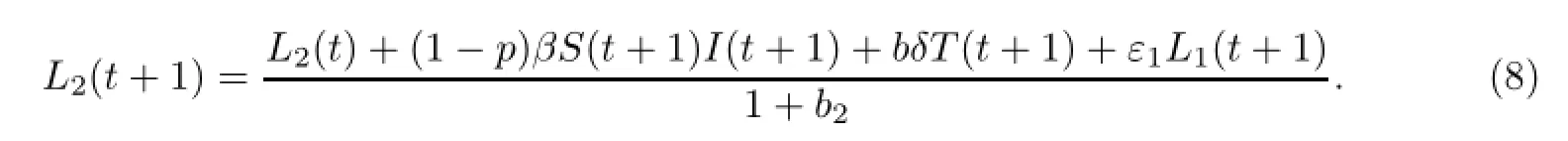
再由模型(2)的第四个方程可得
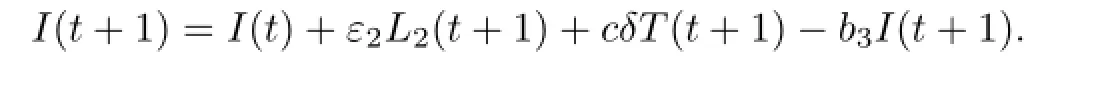
所以
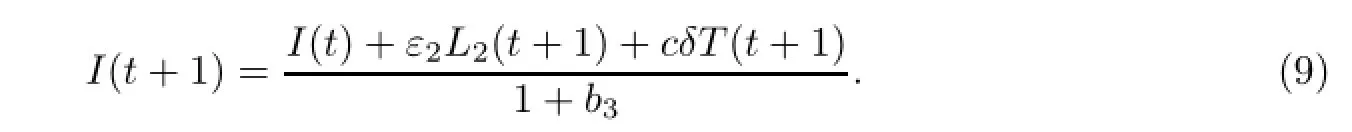
最后由模型(2)的第五个方程可得
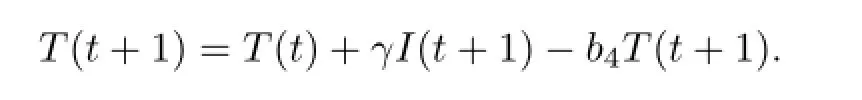
故
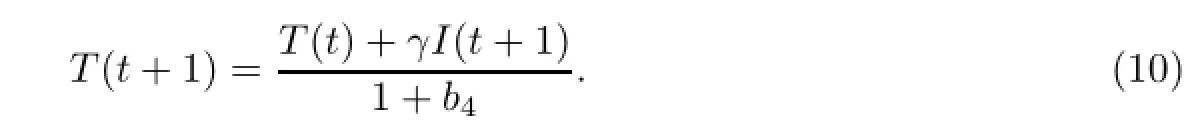
结合式(6)、式(7)、式(8)、式(10),可以得到
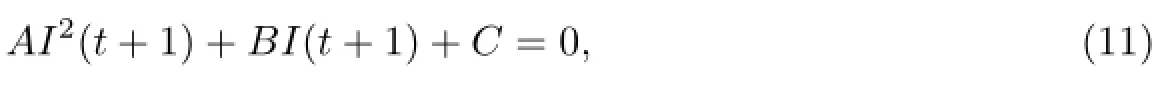
其中
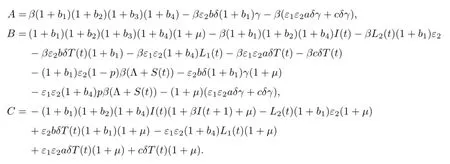
显然,I(t+1)是式(11)的根.因此I(t+1)>0,即I(1)>0.因而,由初始条件式(3)及式(10)可得

进一步,由初始条件式(3)及式(5)可得

结合初始条件(3)及式(7)、式(12)和式(13)可得
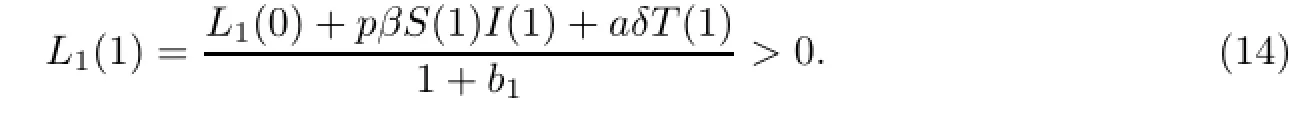
最后,由初始条件(3)及式(8)、式(12)、式(13)和式(14)得
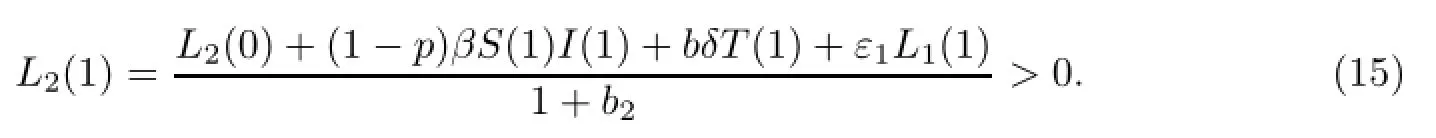
同理可证,S(2)>0,L1(2)>0,L2(2)>0,I(2)>0,T(2)>0.由数学归纳法,假设当t=k时,有S(k)>0,L1(k)>0,L2(k)>0,I(k)>0,T(k)>0,则当t=k+1时有
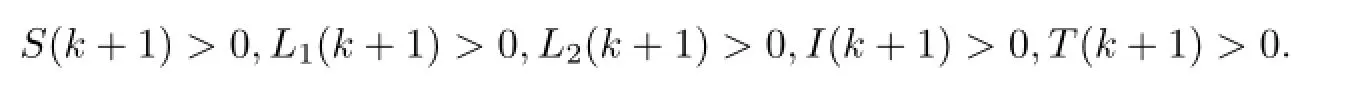
引理得证.
3 平衡点的全局渐近稳定性
定理1当R0<1时,无病平衡点E0是全局渐近稳定的.
证明构造Lyapunov函数
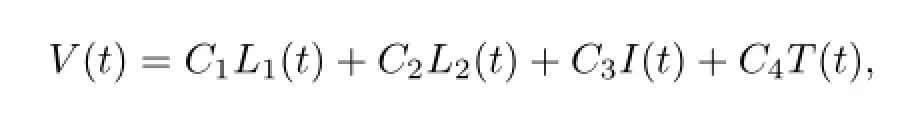
其中,Ci(1=1,2,3,4)均为正常数.则V(t)沿着模型(2)的解的增量
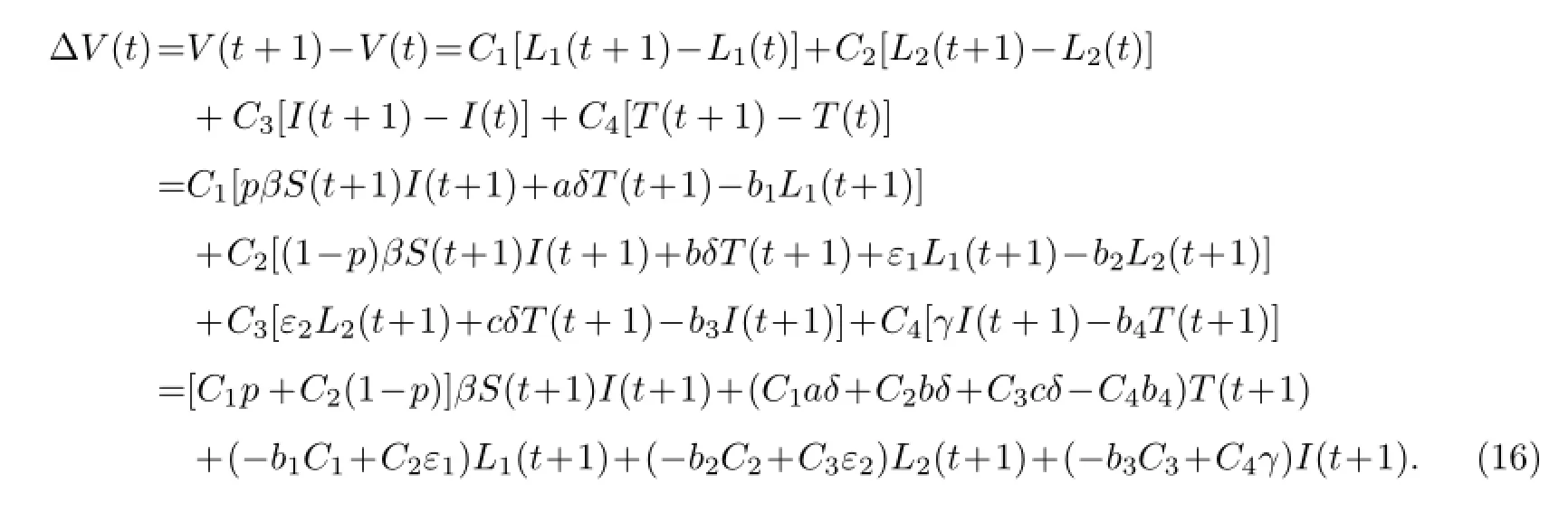
由引理1可得,当(S,L1,L2,I,T)∈Ω时,S(t+1)≤Λ/µ.此时,式(16)变为

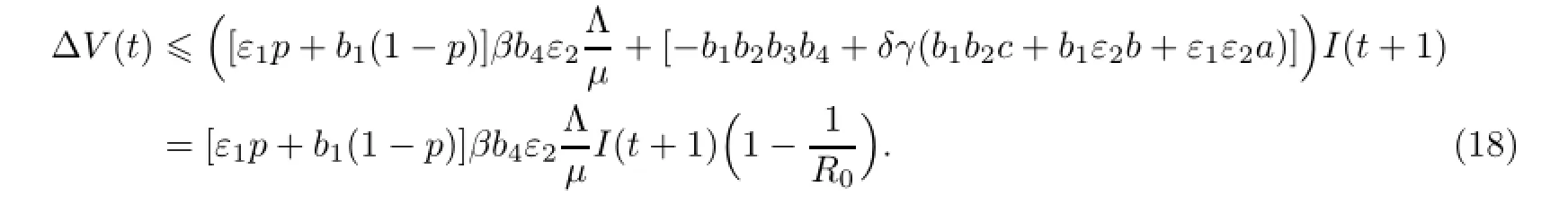
令C1=b4ε1ε2,C2=b4ε2b1,C3=b1b2b4,C4=δ(b1b2c+b1ε2b+ε1ε2a).则不等式(17)变为由不等式(18)可得,当R0<1时,∆V(t)≤0,等号成立当且仅当I(t+1)=0.当I(t+1)= 0时,疾病消失,模型(2)只存在无病平衡点E0,进而由LaSalle-Lyapunov定理[4]可得,无病平衡点E0是全局渐近稳定的.
定理2当R0>1时,地方病平衡点是全局渐近稳定的.
证明考虑函数
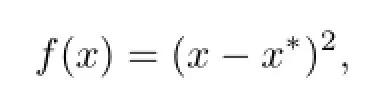
显然,对任意的x,f(x)≥0恒成立.
当R0>1时,模型(2)存在正平衡点).构造Lyapunov函数
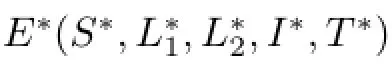

其中
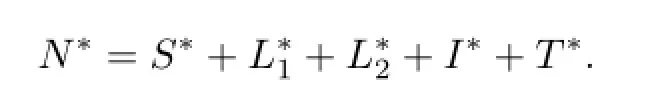
则V(t)沿着模型(2)的解的增量
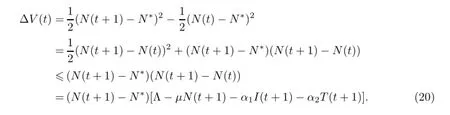
又因为

将方程(21)代入式(20)中得
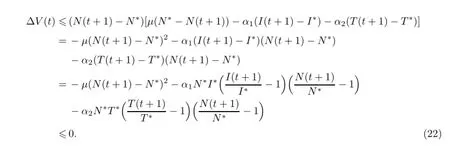
因此,∆V(t)≤0成立,等号成立当且仅当N(t+1)=N∗,I(t+1)=I∗,T(t+1)=T∗.此时,模型的解逼近正平衡点E∗.由LaSalle-Lyapunov定理[4]可得,地方病平衡点E∗是全局渐近稳定的.下面通过数值模拟来说明上述理论结果.
例1在模型(2)中选取一组参数
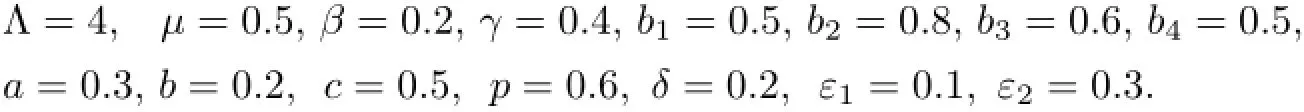
通过计算得到
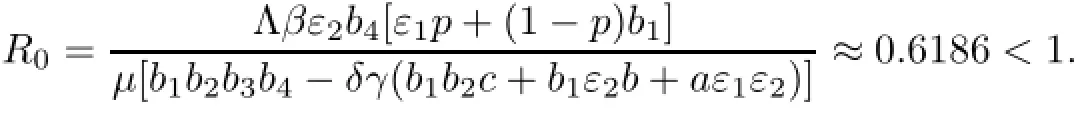
此时,模型(2)存在无病平衡点E0=(8,0,0,0,0),由定理1可得E0是全局渐近稳定的(如图1).
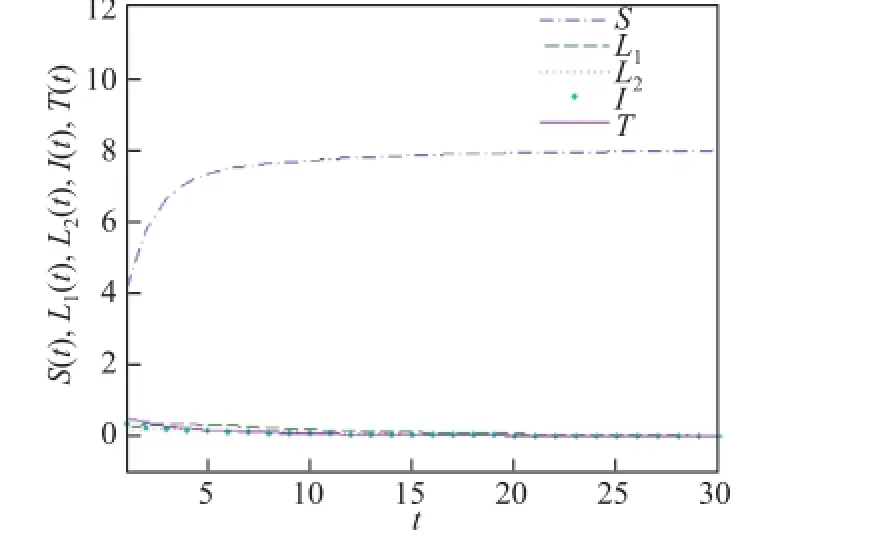
图1 当R0<1时,E0是全局渐近稳定的Fig.1 W hen R0<1,E0is globally asym p totically stable
例2在模型(2)中另选取一组参数:
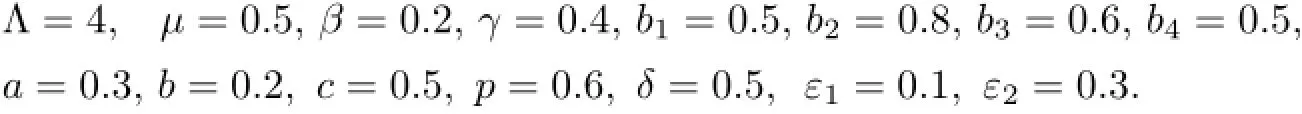
通过计算得到
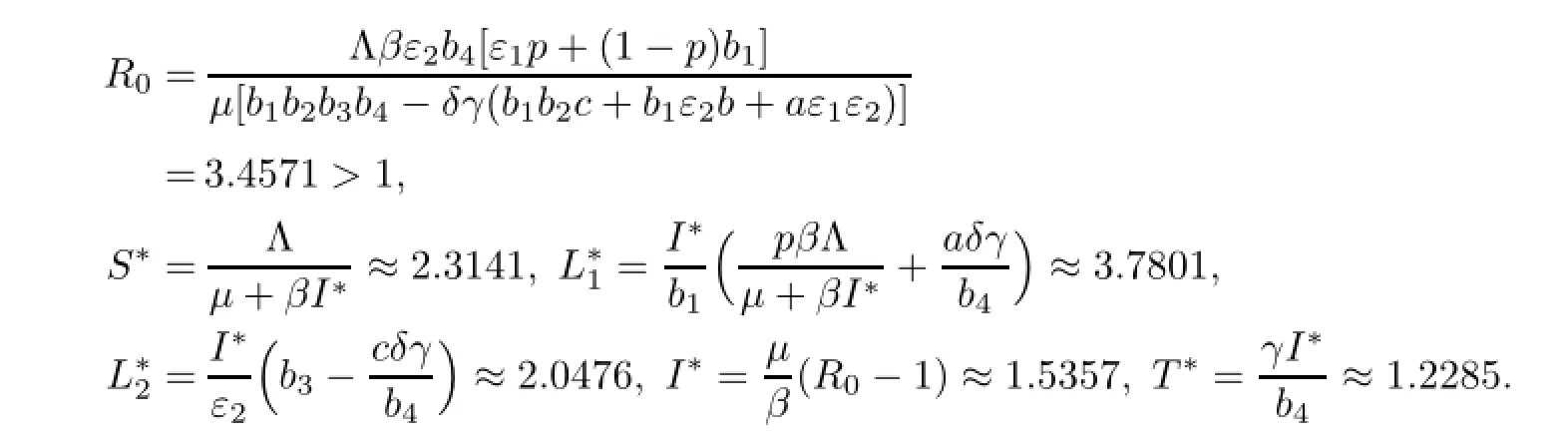
由定理2可得,模型(2)存在地方病平衡点E∗(S∗,L∗1,L∗2,I∗,T∗)是全局渐近稳定的(如图2).
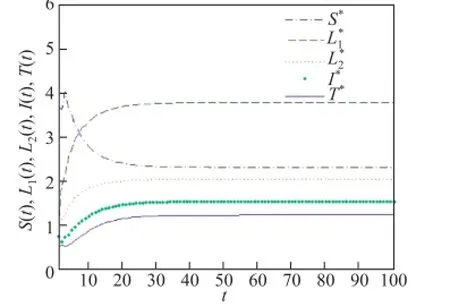
图2 当R0>1时,E*是全局渐近稳定的Fig.2 W hen R0>1,E*is globally asym p totically stab le
4 小结
本文研究了一类离散的结核病模型,考虑了结核病建模过程中的染病快慢因素和治疗因素.通过构造适当的Lyapunov函数,证明了基本再生数R0=1是决定疾病消失或者持续的阈值.当基本再生数R0<1时,无病平衡点是全局渐近稳定的;当基本再生数R0>1时,地方病平衡点是全局渐近稳定的.本文所研究的模型具有两个特点:①模型(2)中参数较多,模型的维数较高,这对模型分析造成了一定困难.②与连续模型相比,本文所构造的离散模型更加直观,便于数值模拟,因为差分方程本身就是一种递推关系,而连续模型也往往需要离散化进行数值计算.
[1]陆征一,王稳地.生物数学前沿[M].北京:科学出版社,2008.
[2]马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.
[3]周义仓,曹慧,肖燕妮.差分方程及其应用[M].北京:科学出版社,2014.
[4]王联,王慕秋.常差分方程[M].乌鲁木齐:新疆大学出版社,1991
[5]BLOW ER SM,M CLEAN A R,PORCO T C,et al.The in trinsic transm ission dynam icso f tubercu losisep idem ics [J].Natu re M ed icine,1995(1):815-821.
[6]OU S C,CHUNG H Y,CHUANG C Y.A b iom ath em atic m od els for tu bercu losis using L yapu nov stab ility fu n ctions[J].Lectu re No tes in Com pu ter Sc ien ce,2010,6377(1):447-453.
[7]CAST ILLO C C,JUN SB.Dynam icalm odels of tubercu losis and their app lications[J].M athem atical Bioscien ce an d E ngineerin g,2004,1(2):361-404.
[8]BOWANG S,TEWA J J.G lobal analysis o f a dynam ica lm odel fo r transm ission of tubercu losis w ith a general con tact ra te[J].Comm un ications in Non linear Science Num erical Sim u lation,2010,15(11):3621-3631.
[9]LIU J L,ZHA NG T L.G loba l stab ility for a tub ercu losis m ode l[J].M athem atica l and Com p u ter M odelling,2011,54(1-2):836-845.
[10]陈娜,周义仓.一类考虑接种的结核病模型的稳定性分析[J].应用数学进展,2012(1):1-11.
[11]ZHOU Y C,K HA N K,FENG Z,et a l.P ro jec tion o f tu bercu losis in c id en ce w ith in c reasing imm igration tren ds [J].Jou rna l o f T heoretica l B io logy,2008,254(2):215-228.
[12]CAO H,ZHOU Y C.The age-stru ctu red SEIT m odel w ith ap p lication to tubercu losis transm ission in china[J]. M athem a tica l and Com pu ter M odelling,2012,55(3-4):385-395.
[13]A LLEN L J S,VA N D EN DR IESSCHE P.T he basic rep rodu ction num b er in som e d iscrete-tim e ep idem icm odels [J].Jou rna l o f D ifferen ce E qu ation s and A pp lica tions,2008,14(5):1127-1147.
(责任编辑李艺)
G lobal stability of a d iscrete tubercu losism odel
CHEN Hui,LILiang-chen
(Basic Courses Department,Ordnance Engineering College,Shijiazhuang050003,China)
In this paper,a d iscrete tubercu losis m odel is investigated.By m eans of calcu lating the nex t generationmatrix’s spectral radius,we derive the rep roduction number R0of the m odel.The solu tions of the m odel are bounded and positive,which can be verified through the relation theory of the difference equation.It is p roved that R0=1 is a threshold to determ ine the disease ex tincation or persistence.The d isease-free equilibrium is global asym p totically stab le when the rep roduction number R0< 1.The endem ic equilib rium is global asym p totically stable when the rep roduction number R0>1.
tubercu losis;the rep roduction number;Lyapunov functions;global asym p totically stab le
1000-5641(2015)06-0072-09
O175.1
A
10.3969/j.issn.1000-5641.2015.06.010
2014-09
国家自然科学基金(11371368)
陈辉,男,硕士研究生,研究方向为微分方程与动力系统.E-mail:15933611905@163.com.
