Lap lace分解法的推广和应用

李亨达，柳银萍

（1.华东师范大学 计算机科学技术系，上海　200241；2.华东师范大学 系统科学研究所，上海　200241）

Lap lace分解法的推广和应用

李亨达1，柳银萍2

（1.华东师范大学 计算机科学技术系，上海200241；2.华东师范大学 系统科学研究所，上海200241）

Adom ian分解法思路简单且应用广泛，但单纯使用Adom ian分解法所获得级数解的收敛范围往往很有限.把Lap lace变换法与Adom ian分解法结合起来求解非线性初边值问题的算法，即为Lap lace分解法.本文将Lap lace分解法推广应用到非线性偏微分方程情形，并针对直接推广得到算法的缺陷，进一步提出了适用于偏微分方程的改进Lap lace分解算法. 以1+1维非线性演化方程为例，阐述了算法的思路和过程.最后通过几个实例，比较了由新算法所获得级数解与Adom ian级数解的精度，由此可看出这些新级数解收敛性更好.

Lap lace分解法；Adom ian分解法；非线性演化方程

0　引　言

宇宙具有很强的非线性性，自然界中的很多现象都可用非线性方程来描述，特别是非线性微分方程；科学研究和工程技术中很多问题的研究都将归结为非线性微分方程的研究，非线性微分方程的解法研究始终是数学物理领域的重中之重.在广大数学物理学家的不断努力下，相继诞生了很多求解方法和算法，如反散射方法[1]、B¨acklund变换和Darboux变换法[2-3]、分离变量法[4-5]、李对称方法[6-7]、Hirota双线性方法[8-9]、齐次平衡法[10-12]、函数展开法[13-14]、辅助方程方法[15]、不变子空间方法[16-19]、摄动方法[20]、Adom ian分解法[21-25]，以及同伦分析方法[26]等.Adom ian分解法由于其计算过程简单，且能用于求解强非线性微分方程及初边值问题而获得了广泛的应用和发展；但单纯使用Adom ian分解法所获得级数解的收敛范围往往很有限.Laplace变换法是求解线性初值问题的一种技巧和算法.近两年有学者将这两种方法结合起来求解一些非线性初值问题，并称之为Lap lace分解法[27-28].但很少有人将该算法应用到非线性偏微分方程情形.本文将Laplace分解法推广应用到非线性偏微分方程情形，但直接推广得到的算法若方程中最高阶导数项不是混合导数项，对Lap lace变换简化后的方程，由Adom ian分解法求得的解分量L［u0］往往不含s，经Laplace逆变换后所得原始方程的解分量u0中包含脉冲函数这样的因子，因此只能求得原始方程的平凡解；但若方程中最高阶导数项是混合导数项，则可构造出原始方程非平凡的解析近似解，见本文例4所示.该推广算法对非线性初边值问题也有效.为了能对上述算法失效的方程也能构造出非平凡解，本文对推广后的算法进一步作了改进，即对Laplace简化后的方程，在采用Adom ian分解法求解时，以Lap lace算子L作为原Adom ian分解法中的最高阶线性算子D，从而可构造出这类方程的非平凡解.美中不足的是改进后的算法只能适用于非线性初值问题.

1　改进的Lap lace分解法

已有的Lap lace分解法主要是针对常微分初值问题，其思路是先通过Lap lace变换简化原始方程，即将常系数非线性常微分方程简化为非线性代数方程，将变系数非线性常微分方程简化为常系数常微分方程；然后应用Adom ian分解法求解简化后的方程，进而通过Laplace逆变换作用在每个解分量上，从而获得原始方程的解析近似解.大量实例表明，Lap lace分解法较单纯Adom ian分解法所获得解级数的收敛性更好[27-28].下面我们将已有的Laplace分解法推广应用到偏微分方程情形.需要说明的是非线性偏微分方程往往关于一个变量的导数只出现在线性项上，关于另一个变量的导数可能出现在非线性项上，如1+1维非线性演化方程；往往关于时间变量t的导数只出现在线性项上，关于空间变量x的导数可能出现在非线性项中.因此直接推广得到的算法，即先对t作Lap lace变换简化原始方程，简化后的方程为关于x的非线性常微分方程，把s看作参数.应用Adom ian分解法求解简化后的方程，此时Adom ian分解法中的最高阶线性算子D一般应取方程中关于x的最高阶导数项.若该最高阶导数项是关于x和t的混合导数项，则该算法完全可以构造出原始方程的非平凡解析近似解，且该算法也能适用于非线性初边值问题，如本文例4所示；若方程中的最高阶导数项不是关于x和t的混合导数项，由Adom ian 分解法求出的第一个解分量L［u0］往往不含s，则通过Lap lace逆变换后所获得原始方程的第一个解分量u0将包含脉冲函数δ（t）这样的因子，故往往只能构造出原始方程的平凡解.对这类方程，本文将Lap lace分解法作了适当改进，即以Laplace算子L作为Adom ian分解法中的最高阶线性算子D，从而可获得非线性初值问题非平凡的解析近似解.改进后的算法思路和过程如下.

考虑非线性偏微分方程

初始条件为u（x，0）=h（x），ut（x，0）=f（x），其中u=u（x，t），D代表最高阶线性算子D= ∂n/∂tn，Ru代表线性剩余项，N u代表非线性项，g（x，t）为源项.

第一步，对方程两边同时应用Lap lace变换（下文统一记作L）得

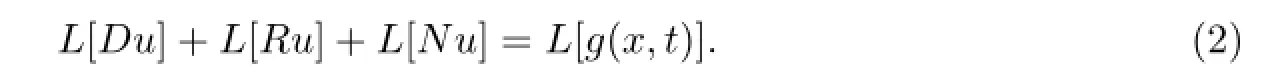
由Lap lace变换的微分性质，可以得到

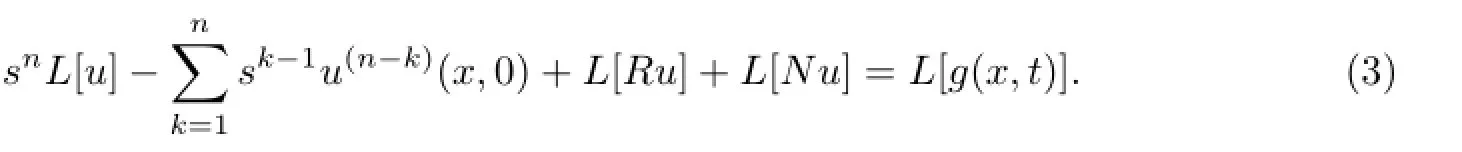
化简得到

第二步，将方程的解u及非线性项N u分别表示为无穷级数

其中Am代表Adom ian 多项式，其计算公式为

将式（5）代入式（4），得到

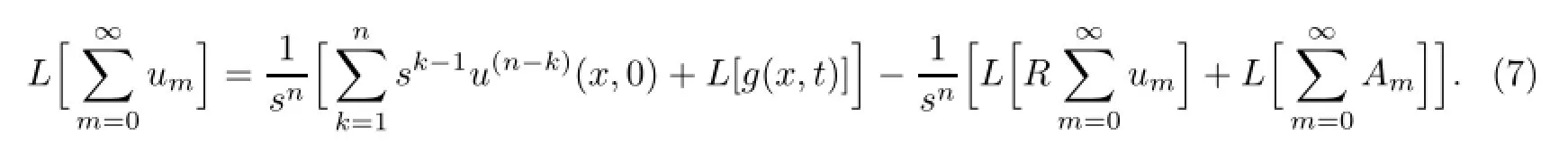
由此可得到迭代公式

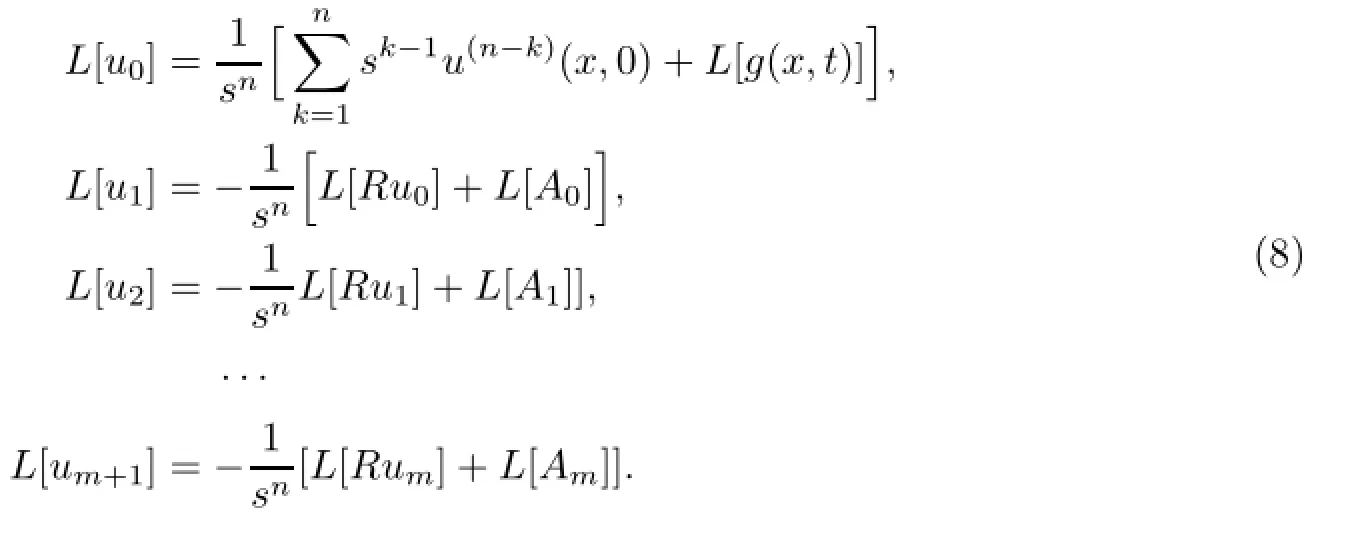
第三步，迭代地对式（8）中的每个方程进行化简并应用Laplace逆变换，可依次求得解分量u0，u1，u2，···最终，可得到原方程的m阶解析近似解为

需要指出的是，前一种思路可适用于非线性初边值问题，而改进后的算法只能用于求解非线性初值问题.下面通过几个具体实例来说明本文算法的有效性.

2　应用举例

例1考虑KdV方程[29]

初始条件为u（x，0）=-6sech2（x）.

采用改进后的算法对方程两边同时应用Laplace变换并代入初始条件得

化简得到

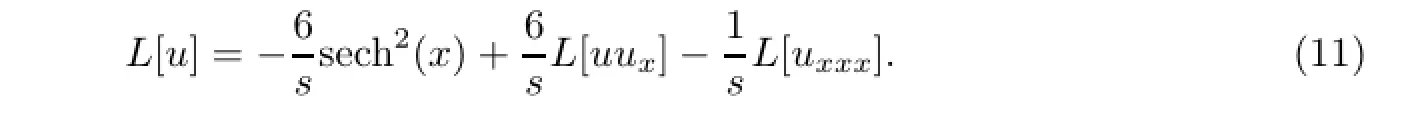
将式（5）代入式（11）有

其中Am是由非线性项uux得到的Adom ian多项式.相应于式（8）的迭代公式为

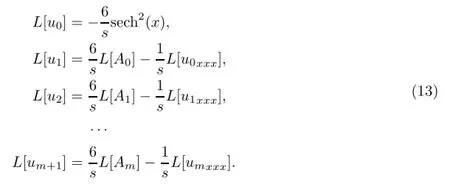
依次迭代地对式（13）进行化简，并应用Lap lace逆变换得到

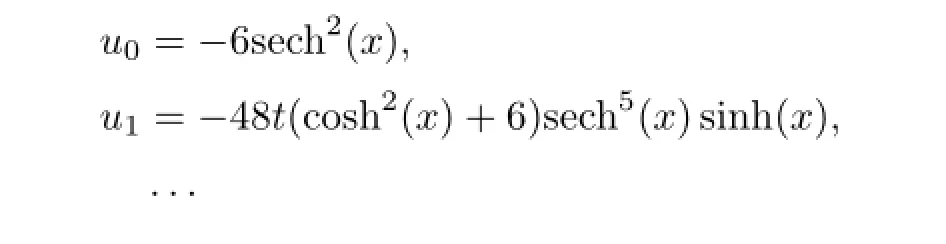
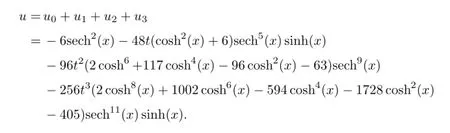
则所获得3阶解析近似解同理可计算得到5阶、10阶解析近似解等.

图1展示了不同阶解析近似解与文献［29］中的Adom ian级数解及精确解之间的比较曲线.从图中可看出，由Lap lace分解法获得的级数解与Adom ian级数解拟合得很好，3阶近似解与精确解误差很大，但5阶近似解较好地收敛到了精确解.

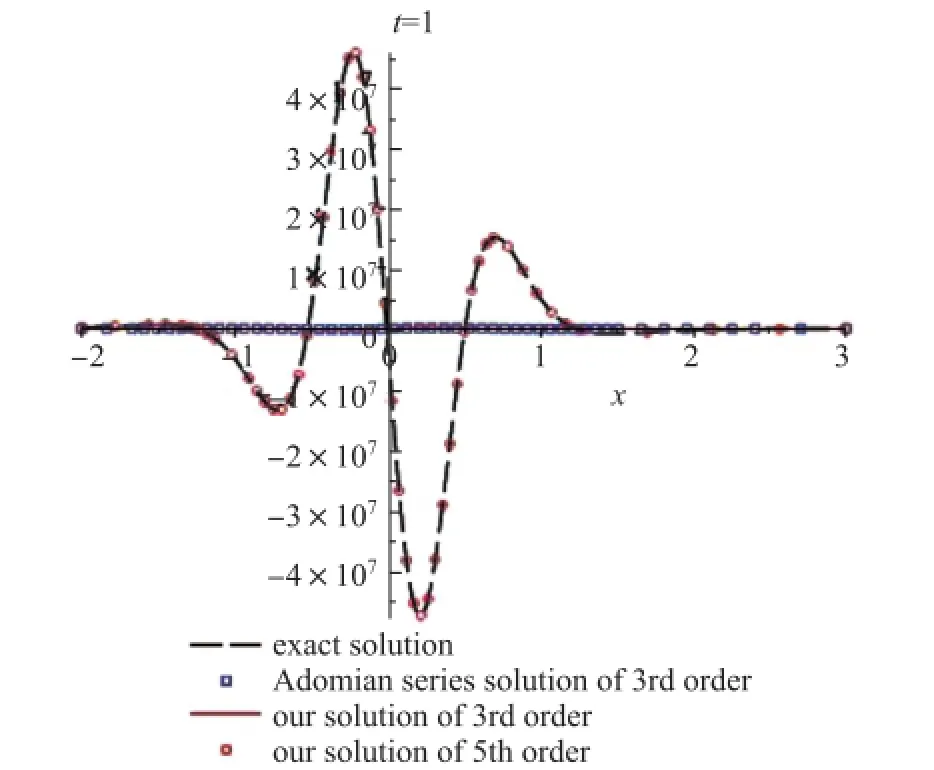
图1　t=1时本文不同阶近似解与精确解、Adom ian级数解的比较曲线Fig.1　Com parison curves between our solutions of different orders，exact solution and Adom ian series solution at t=1

为了进一步说明5阶近似解的精度，图2展示了不同时刻解的误差曲线.从曲线的走向可以看出，该解至少在区域｛（x，t）|0≤t≤10，-∞＜x＜∞｝内具有很高的精度，且随着阶数的升高，时间域的收敛范围越来越大，精度也越来越高，如10阶近似解在t=10时，误差降到小于10-22数量级.

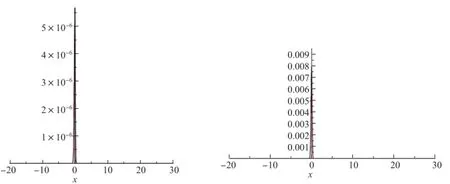
图2　t=1（左图）和t=10（右图）时5阶近似解的误差曲线Fig.2　Error cu rves of ou r solu tions of 5th order at t=1（left side）and t=10（right side）

例2考虑K lein—Gordon方程[30]

初始条件为u（x，0）=0，ut（x，0）=0.

采用改进后的算法对方程两边同时应用Laplace变换并代入初始条件得

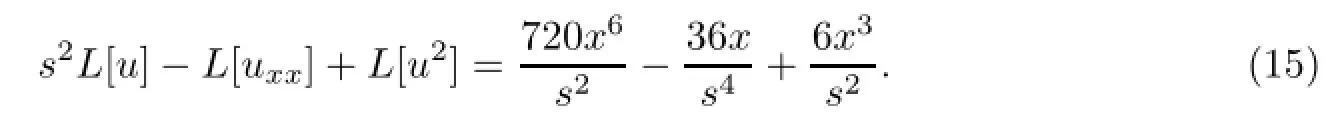
将式（5）代入式（15）有

其中Am是由非线性项u2得到的Adom ian多项式.由此可得到迭代公式

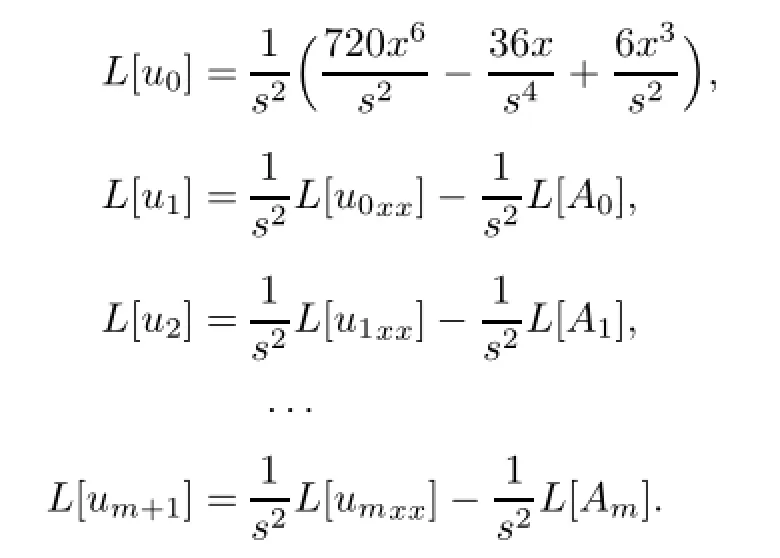
对迭代式依次应用Lap lace逆变换求解得到

由以上解分量获得的解析近似解与Adom ian级数解及已有的精确解进行比较，结果如图3、图4所示.

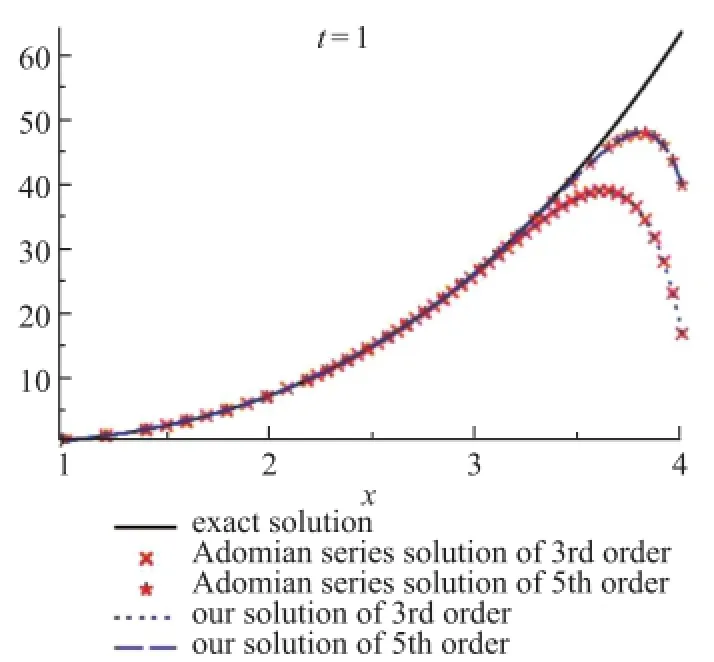
图3　本文近似解与精确解，Adom ian级数解的比较曲线Fig.3　Com parison curves between our solutions，exact solution and Adom ian series solutions

从图中可以看出，我们的解析近似解与同阶的Adom ian级数解基本重合，且阶数越高，近似解越逼近精确解，收敛范围也逐步增大.图5、图6展示了不同时刻20阶近似解与60阶近似解的误差曲线.显然，60阶近似解的精度更高，当取t=1.5时其收敛区间为｛x|-2＜x＜2｝.

图4　本文不同阶近似解与精确解的比较曲线Fig.4　Com parison curves between our solutions of different orders and exact solution

图5　t=0.5时20阶近似解（左图）与60阶近似解（右图）的误差曲线Fig.5　Error curves of our solutions of 20th order（left side）and 60th order（right side）at t=0.5

例3考虑K lein—Gordon方程[31]

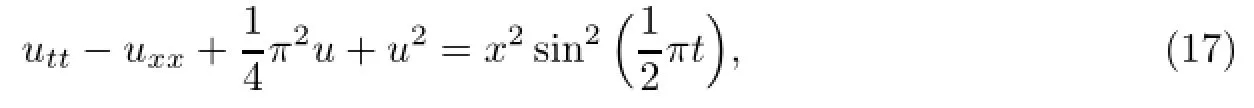
对方程两边同时进行Laplace变换得到

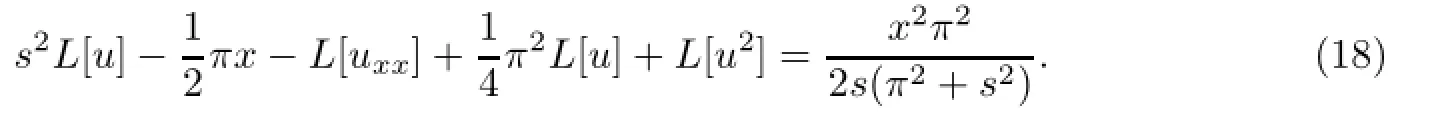
化简得到

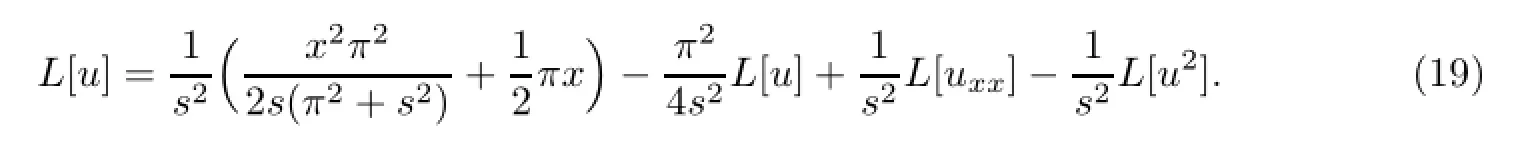
将式（5）代入式（20）有

其中Am是由非线性项u2得到的Adom ian多项式.可得迭代公式

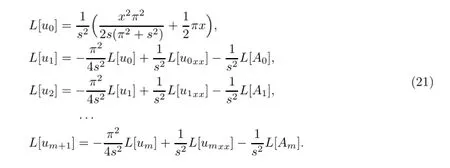
对各迭代式依次应用Laplace逆变换可求得方程（18）的各个解分量.限于篇幅在此不列出其表达式.

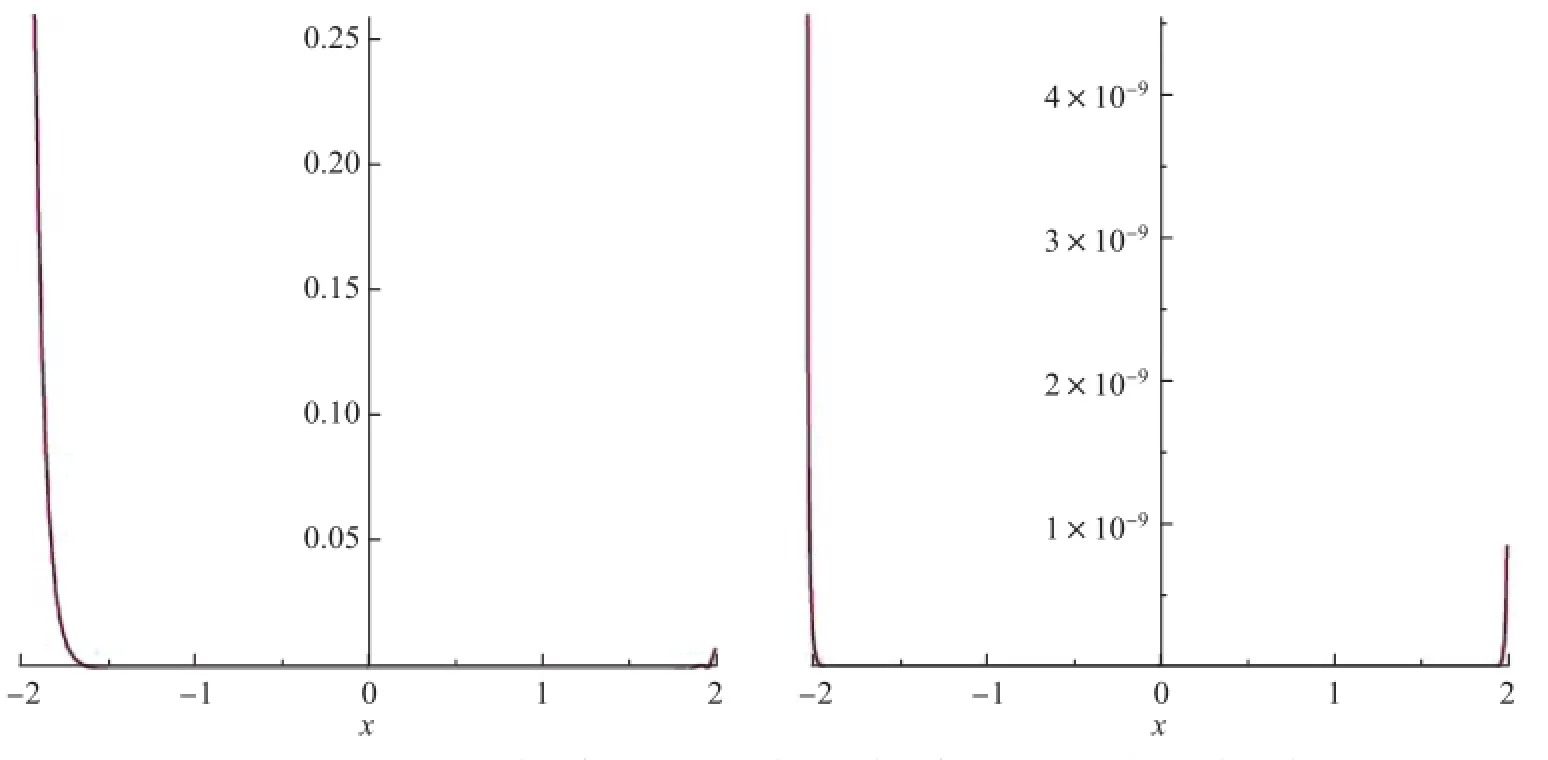
图6　t=1.5时20阶近似解（左图）与60阶近似解（右图）的误差曲线Fig.6　Error cu rves of ou r solu tions of 20th order（left side）and 60th order（right side）at t=1.5

图7、图8展示了本文改进的Lap lace分解法求得的解析近似解与文献［31］中的Adom ian级数解、精确解的比较曲线.

从图7、图8可以看出，由本文改进的Lap lace分解法所获得的解析近似解与精确解吻合得很好，而Adom ian级数解随着x或t增大愈来愈偏离精确解.但需要说明的是，该实例计算过程中“中间表达式”急剧膨胀，因此，我们最高只算到了5阶.图9给出了2阶与5阶近似解的误差比较曲线.从图9中可看出5阶近似解的精度略高，且5阶近似解在区域｛（x，t）|-1＜x＜1，0≤t≤0.5｝内具有较高的精度.

图7　（a）x=0.1时的比较曲线；（b）x=0.3时的比较曲线；（c）x=0.5时的比较曲线Fig.7　（a）Com parison curves at x=0.1；（b）Com parison cu rves at x=0.3；（c）Com parison curves at x=0.5

图8　（a）t=0.1时的比较曲线；（b）t=0.5时的比较曲线；（c）t=0.9时的比较曲线Fig.8　（a）Com parison curves at t=0.1；（b）Com parison curves at t=0.5；

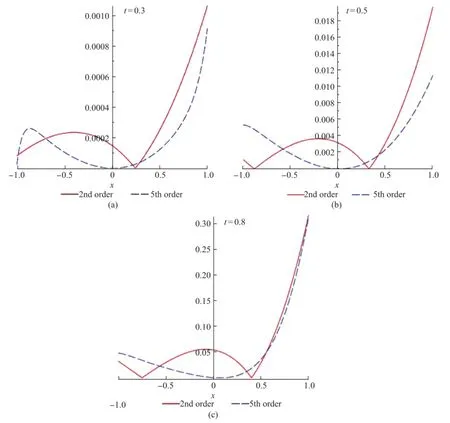
图9　（a）t=0.3时的误差曲线；（b）t=0.5时的误差曲线；（c）t=0.8时的误差曲线Fig.9　（a）Error curves at t=0.3；（b）Error curves at t=0.5；（c）Error curves at t=0.8

例4考虑非齐次Rosenau—RLW方程[32]

初始条件为

边界条件为

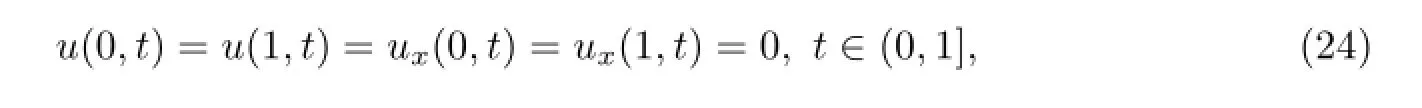
其中

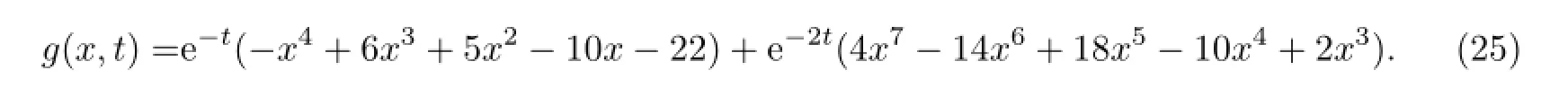
文献［32］中式（6.4）给出了该系统的一个精确解为

本例中方程的最高阶导数项uxx xx t是混合导数项.我们采用直接推广得到的算法求解该方程，即对方程两边同时进行Laplace变换并代入初始条件化简得到

此时，方程（28）可视为关于x的常微分方程，整理得到

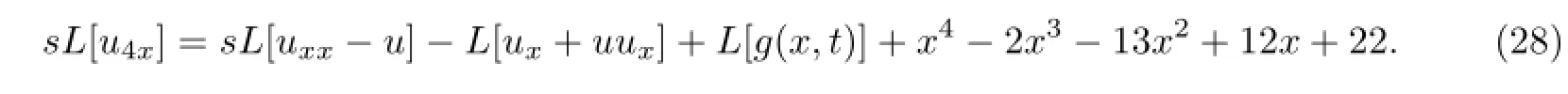
采用Adom ian分解法求解，线性算子D即为对x求四阶导数，其逆算子D-1即为对x求四次积分.可得到迭代公式

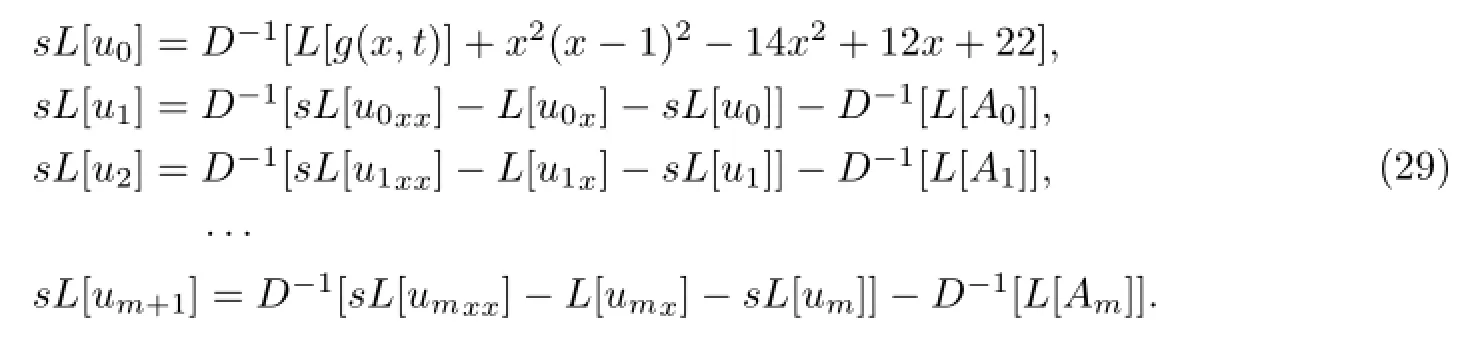
依次对各迭代式进行化简并应用Lap lace逆变换可得到原方程的各个解分量，由此获得不同阶解析近似解.将本文得到的解析近似解与精确解比较，结果如图10所示.

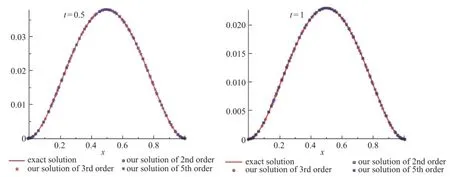
图10　t=0.5和t=1.0时不同阶近似解与精确解的比较曲线Fig.10　Com parison curves between our solutions of differentorders and exact solution at t=0.5 and t=1.0

从图中可以看出，由直接推广得到的算法求得的解析近似解与精确解吻合得很好.该实例是初、边值问题，x，t的取值均在区间（0，1］内.通过反复测试得知，我们的10阶近似解在整个区间内均有很高的精度，见图11所示.

3　结论

构造微分方程解析解的方法有很多，但每一种方法都有各自的优缺点和适用范围.有时候将两种已有的算法结合起来使用可获得更好的结果.Lap lace分解法就是将Lap lace变换法和Adom ian分解法结合起来构造非线性微分系统解析近似解的一种算法.大量的实例表明Laplace分解法所获得的级数解较单纯Adom ian分解法的级数解收敛性更好.本文将Lap lace分解法推广到了非线性偏微分方程情形，直接推广后的算法仅对线性最高阶导数项是混合导数项的方程有效.本文进一步提出的改进算法对线性最高阶导数项是混合导数项和非混合导数项的方程均有效，且改进后的算法也完全适用于常微分方程.我们在计算机代数系统Maple平台上完全实现了改进后的算法，其中的软件包可自动推导出所输入方程的解析近似解.限于篇幅，软件包的工作将在后面的文章中报道.

图11　（a）t=0.1时的误差曲线；（b）t=0.5时的误差曲线；（c）t=0.8时的误差曲线Fig.11　（a）Error curves at t=0.1；（b）Error curves at t=0.5；（c）Error cu rves at t=0.8

[1］GARDNER C，GREENE J，KRUSKAL M，et a l.M ethod for solving the K ortew egde Vries equation[J].Physical Review Letters 1967，19（19）:1095-1097.

[2］FAN E G，ZHANG H Q.B¨ack lund transform ation and exact solu tions for W hitham-B roer-K aup equations in shallow water[J].App lied M athem atics and M echanics，1998，19（8）:713-716.

[3］ROGERS C，SCH IEF W.B¨ack lund and Da rboux T ransfo rm ations:Geom etry and M odern A pp lications in So liton Theory[M].Cam b ridge:Cam b ridge University Press，2002.

[4］LOU S Y，LU J Z.Special so lu tions from the variab le separation app roach:The Davey-Stewartson equation[J]. Jou rnal o f Physics A:M a them atical and Genera l，1996，29（14）:4209-4215.

[5］ZHANG S L，LOU S Y，QU C Z.Variab le separation and exact solu tions to generalized non linear d iffusion equa tions[J].Chinese Physics Letters，2002，19（12）:1741-1744.

[6］O LVER P J.A p p lica tions o f Lie G rou ps to D ifferen tia l Equa tions[M].Berlin:Sp ringer-Ver lag，1993.

[7］CRADDOCK M.Fundam ental so lu tions，transition densities and the in tegration of Lie symm etries[J].Jou rnal of D ifferen tia l Equations，2009，246（6）:2538-2560.

[8］HU X B，TAM H W.A p p lication o f H irota，s b ilin ear form a lism to a tw o-d im ensiona l lat tice by Lezn ov[J]. Phy sics Letters A，2000，276（1）:65-72.

[9］HU X B，W U Y T，GENG X G.H irota b ilinear app roach to a new in tegrab le d ifferen tial-d ifference system[J]. Jou rn a l o f M athem atica l Phy sics，1999，40（4）:2001-2010.

[10］李志斌.非线性数学物理方程的行波解[M].北京:科学出版社，2007.

[11］W ANG M L，ZHOU Y B，L I Z B.A pp lication o f a hom ogeneous ba lan ce m ethod to exa ct so lu tions o f non linear equa tions in m a them atica l physics[J].Physics Let ters A，1996，216（1）:67-75.

[12］范恩贵.齐次平衡法、W eiss-Tab or-Carn eva le法及C larkson-K ru ska l约化法之间的联系[J].物理学报，2000，49（8）: 1409-1412.

[13］FAN E G，ZH ANG J.A p p lications o f the Ja cob i e llip tic fu n ction m eth od to sp ec ia l-typ e n on linea r equations[J]. Phy sics Letters A，2002，305（6）:383-392.

[14］LIU Y P，LIZ B.An au tom ated Jacobi ellip tic function m ethod for find ing period ic wave solu tions to non linear evolu tion equa tions[J].Chinese Physics Letters，2002，19（9）:1228-1230.

[15］SIRENDAOREJI，SUN J.A ux iliary equ ation m ethod for so lv ing non lin ear p artia l d ifferen tia l equations[J]. Phy sics Letters A，2003，309（5）:387-396.

[16］SV IRSHCHEVSK IIS R.Inva rian t linea r spaces and exact solu tions of non linear evolu tion equations[J].Jou rnal of Non linear M athem atical Physics，1996，3（1-2）:164-169.

[17］GA LAK T IONOV V A，SV IRSHCHEVSK II S R.Exac t so lu tions an d invariant subspaces o f non linear par tia l d ifferen tial equations in m echanics and physics[M].Boca Raton:Chapm an&Hall/CRC，2010.

[18］QU C Z，ZHU C R.C lassification o f cou p led system s w ith tw o-com p onent non linear d iffu sion equ ation s by th e invarian t sub spa ce m ethod[J].Jou rna l o f P hysics A:M athem a tica l and Th eoretica l，2009，42（47）:475201.

[19］M A W X.A refined invarian t subspace m ethod and app lica tions to evo lu tion equations[J].Science Ch ina M athem atics，2012，55（9）:1769-1778.

[20］H INCH E J.Per tu rba tion M ethods（Cam b ridge Tex ts in A pp lied M a them atics）[M].Cam b rid ge:Cam b ridge Un iversity P ress，1991.

[21］ADOM IAN G.Solv ing Frontier Prob lem so f Physics:The Decom position M ethod[M].Boston:K luwer A cadem ic Pub lishers，1994.

[22］ADOM IA N G.A rev iew o f the decom p osition m ethod an d som e recen t resu lts for non linear equations[J]. Com pu ters and M ath em atics w ith A p p lications 1991，21（5）:101-127.

[23］LIN Y Z，LIU Y P，LI Z B.Sym bo lic com pu tation of analy tic ap p rox im a te solu tions for non linear fractional d ifferen tia l equ ation s[J].Com p u ter Physics Com m un ications，2013，184（1）:130-141.

[24］RACH R C.A new definition of the Adom ian po lynom ials[J].K ybernetes，2008，37（7）:910-955.

[25］DU AN J S.A n effic ien t a lgorithm fo r the m u ltivariab le A dom ian p o lynom ia ls[J].A pp lied M ath em atics an d Com pu tation，2010，217（6）:2456-2467.

[26］LIAO S J.Beyond Pertu rbation:In troduction to the Hom otopy A nalysis M ethod[M].Boca Raton:Chapm an &Ha ll/CRC，2004.

[27］YUSUFOG LU E.N um erica l so lu tion o f D u ffing equa tion by th e Lap lace decom p osition a lgo rithm[J].A pp lied M athem atics and Com pu tation 2006，177（2）:572-580.

[28］KHAN Y，AUSTIN F.App lica tion o f the Lap lace decom position m ethod to non linear hom ogeneous and nonhom ogenous advection equations[J].Zeitsch rift f¨u r Natu rforschung-A，2010，65（10）:849-853.

[29］W AZW AZ A M.Constru ction o f so litary w ave so lu tions an d rationa l so lu tions for the K d V equation by A dom ian decom p osition m ethod[J].Chaos，So liton s and Frac ta ls，2001，12（12）:2283-2293.

[30］WAZWAZ A M.Them od ified decom position m ethod for analy tic trea tm en t of d ifferen tia l equations[J].A pp lied M athem atics and Com pu tation 2006，173（1）:165-176.

[31］BA SAK K C，RAY P C，BERA R K.So lu tion o f n on-linear K lein-G ordon equation w ith a quad ratic non-linea r term by Adom ian decom position m ethod[J].Comm unica tions in Non linear Science and Num erical Sim u lation，2009，14（3）:718-723.

[32］ATOU AN I N，OM RAN I K.G a lerk in fin ite e lem en t m ethod for the Rosenau-RLW equation[J].Com p u ters an d M athem atics w ith A p p lications，2013，66（3）:289-303.

（责任编辑李艺）

Ex tension of the Lap lace decom p osition m ethod and its app lication

LIHeng-da1，LIU Y in-p ing2
（1.Departm en t of Com puter Science and Technology，East China Norm al University，Shanghai200241，China；2.Institute of System Science，East China Normal University，Shanghai 200241，China）

The Adom ian decom position method was sim p le and widely used in solving non linear differential equations.The convergence region of the Adom ian series solution is always very lim ited.Therefore the Laplace decom position method，which is a combination of Lap lace transformation method and Adom ian decom position method，is p roposed to solve initial boundary value p rob lem s.In this paper，the Laplace decom position method is extended to solve non linear partial differential equations.For the flaws of the directly ex tended algorithm，we further p roposed a modified algorithm to solve non linear partial differential equations.Take，for exam p le，1+1 dimensional non linear evolution equation to expound the idea and p rocedure of the algorithm.Finally，several exam ples were given to demonstrate the high p recision and large convergence region of the new solutions by com paring these new solutions with those Adom ian series solutions aswell as other known exact solutions.

Laplace decom position method；Adom ian decom position method；non linear evolution equation

O 175.29

A

10.3969/j.issn.1000-5641.2015.06.009

1000-5641（2015）06-0059-13

2014-08

国家自然科学基金重点项目（11435005）

李亨达，女，硕士研究生，研究方向为符号计算.E-mail：gyyzlihengda@163.com.

柳银萍，女，教授，研究方向为符号计算、数学机械化.E-mail：ypliu 2@hotmail.com.