面基层间不同结合状态下发射场坪动态响应研究
2015-09-18周晓和马大为朱忠领廖选平鞠晓杰中国运载火箭技术研究院北京00076南京理工大学机械工程学院江苏南京0094
周晓和,马大为,朱忠领,廖选平,鞠晓杰(.中国运载火箭技术研究院,北京00076;.南京理工大学机械工程学院,江苏南京0094)
面基层间不同结合状态下发射场坪动态响应研究
周晓和1,马大为2,朱忠领2,廖选平1,鞠晓杰1
(1.中国运载火箭技术研究院,北京100076;2.南京理工大学机械工程学院,江苏南京210094)
为了得到面基层间不同结合状态下无依托发射场坪的动态响应,基于Cohesive单元的双线性内聚力本构,建立了层间结合数学模型,进一步建立了含层间效应的发射场坪数值模型;引入初始损伤变量并结合应变等价性假设,建立了层间不同结合状态数学模型;以含层间效应的发射场坪数值模型为基础,完成了面基层间不同结合状态下的发射场坪数值模型的建立,分析了发射筒底部处场坪面基层间界面的损伤分布与演化,研究了面基层间不同结合状态下发射场坪动态响应的变化。结果表明:当面基层间结合状态一定时,发射筒底部对地载荷作用边界处面基层间界面损伤最严重,且沿着载荷作用区域半径方向,面基层间界面损伤分布表现为先增加、后减小的规律;随着面基层间结合状态的变差,沿载荷作用区域半径方向,面基层间界面损伤演化表现为中间不变、两边减小的规律,场坪面层垂向位移和水平位移产生不同程度的变大,面层、基层层底中心最大应力均变小。
兵器科学与技术;发射场坪;层间界面;内聚力本构;初始损伤;动态响应
0 引言
随着导弹命中精度和空间侦察技术的不断提高,远程战略导弹采用地下井式热发射及通过增加地下井的抗超压能力来保护导弹变得越来越不可靠。因此,一些国家相继研制出了各种陆基机动发射方式[1-2]。无依托发射就是导弹发射不再依托预准备的发射场地,而是随机选取场地发射,该方式具有机动地域广阔、速度快、生存能力高和攻击能力强等特点。我国的公路修筑不仅覆盖面广阔且错综复杂,将公路作为发射场坪不仅满足了导弹发射的随机性、隐蔽性,更提高了导弹的机动性。
某导弹的无依托发射,要求在各等级公路上均可实现安全发射,这对路面的使用性能提出了较高的要求。路面各层间结合作用的强弱,将导致其工作状态的不同及力学响应的差异[3-4],故路面各层间结合状态的优劣是影响其使用性能的重要因素,所以进行层间不同结合状态下发射场坪动态响应研究具有重要意义。目前国内外学者对道路层间结合的研究有许多不同的方法及模型,采用的古德曼模型形式简洁,但只考虑了不同功能层在剪应力下的水平位移响应[5-8];黄宝涛等[9]、艾长发等[10]使用的两节点层间接触模型,通过定义法、切向弹簧来表征层间接触面上的力学行为,并没有将层间摩擦效应考虑在内;赵炜诚等[11]使用的层间接触模型,虽在弹簧模型的基础上考虑了摩阻作用,但该模型并不能动态反映损伤累积所带来的层间刚度的折损;李彦伟等[12]采用脱层失效理论,虽从细观角度对道路层间结合状态进行了分析,但由于没有对带有初始损伤的层间界面进行本构定义,故无法对层间不同结合状态下的发射场坪动态响应进行研究。
本文在基于Cohesive单元的双线性内聚力本构建立层间结合数学模型的基础上,引入初始损伤变量并结合应变等效性假设,推导层间不同结合状态下的双线性内聚力本构,建立层间不同结合状态数学模型。以含层间效应的发射场坪数值模型为基准,层间不同结合状态的数学模型为理论依据,建立面基层间不同结合状态的发射场坪数值模型。通过数值计算,得到发射筒底部处场坪的动态响应及其变化,重点研究面基结合层的损伤分布及变化,并对面基层间不同结合状态与场坪动态响应间的耦合效应进行一定的阐释。研究结果可为导弹无依托射前场坪快速评估提供理论支撑。
1 数学模型的建立
1.1内聚力本构模型
内聚力模型在内聚力区域内由两个假想的面定义,内聚力区域为材料裂缝尖端与内聚力区域尖端之间的区域,如图1所示。其中:Tn为法向内聚力。假想面通过内聚力结合在一起,而内聚力的大小取决于两个面的张开位移。在内聚力区域中裂缝尖端的内聚力为0,内聚力区域尖端的内聚力最大[13]。

图1 内聚力模型示意图Fig.1 Cohesion model
内聚力本构通过内聚力一位移曲线定义,如图2所示。其中:T为内聚力;δ为两个假想面的相对位移;Tmax为开裂强度,是内聚力所能达到的最大值;δf为两个假想面的失效位移。内聚力模型本构假定:当δ≤δ0时,内聚力区域的材料为线弹性;当δ0<δ<δf时,材料进入损伤软化阶段;当δ≥δf时,材料发生断裂破坏。
1.2层间结合数学模型
采用双线性内聚力模型本构,建立层间结合数学模型,其中双线性内聚力模型本构可通过Cohesive单元实现[14]。
层间结合数学模型中,在内聚力达到开裂强度之前,内聚力区域材料表现为线弹性,如图2所示。其上升段斜率为层间界面刚度。当层间界面厚度为h时,界面模量与界面刚度间关系为
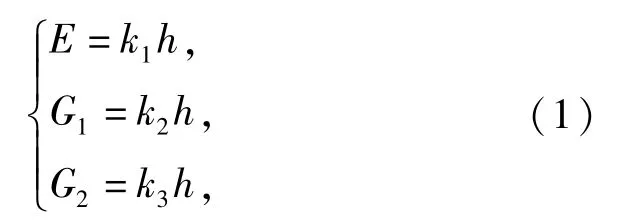
式中:k1、k2、k3分别为层间界面3个方向刚度;E为界面法向方向弹性模量;G1、G2为沿不同切向的剪切模量。
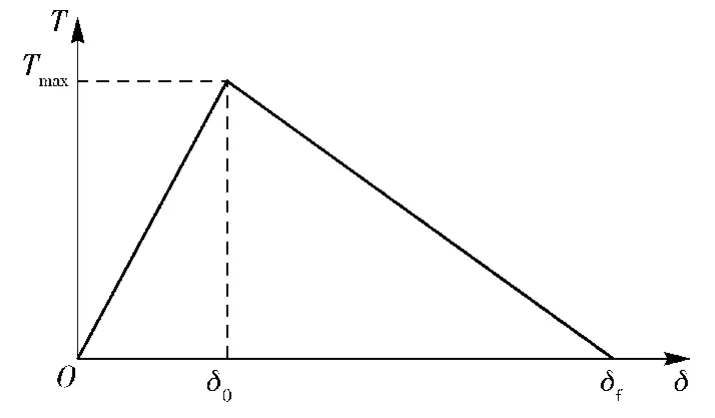
图2 内聚力模型内聚力位移曲线Fig.2 Displacement curve of cohesionmodel
参考模拟层间作用弹簧的刚度计算方法,界面法向刚度计算表达式[11]为

式中:Ss、Sb、Si分别为沥青路面面层、基层、夹层的法向刚度;h1、E1、μ1分别为面层的厚度、弹性模量、泊松比;h2、E2、μ2分别为基层的厚度、弹性模量、泊松比;h3、E3、μ3分别为夹层的厚度、弹性模量、泊松比。
界面处切向刚度计算表达式[11]为

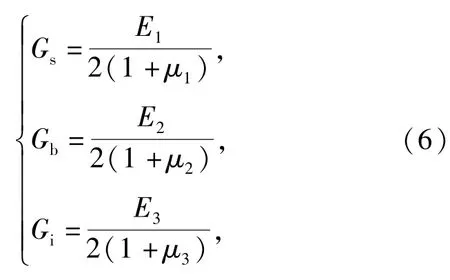
式中:Gs、Gb、Gi分别为面层、基层、夹层的剪切模量。
当层间界面内聚力达到开裂强度后,层间界面表现为损伤软化,其损伤因子计算式[13]为
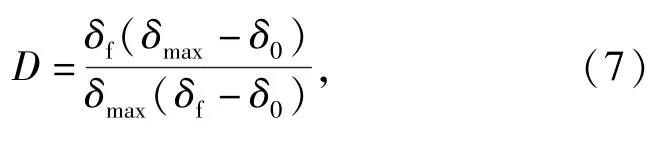
式中:δmax为加载过程中界面张开位移达到的最大值。D=0表示内聚力区域的材料无损伤;D=1表示内聚力区域的材料断裂。
1.3层间不同结合状态数学模型
层间界面内聚力本构数学模型有两个独立参数:开裂强度Tmax和失效位移δf,其中,对于既定结构的发射场坪,层间界面失效位移δf一定。由于无依托发射对发射场坪的选取具有随机性,不同的道路由于在使用过程中所经历的载荷和所处的自然环境不同,将导致其力学性能不同。对于新铺设的道路,其层间界面各项力学指标均可达到使用标准,而对于具有一定寿命的道路,层间界面存在不同程度的损伤甚至破坏,这将引起发射场坪层间界面刚度的下降,使得界面的实际刚度将低于理论界面刚度,进一步影响层间界面的开裂强度的大小。
为表征由于道路层间界面初始损伤而引起的发射场坪层间界面的不同状态,引入初始损伤变量0≤d≤1.由于层间界面损伤引起的刚度折剪为不可逆,且失效位移δf一定,故发射场坪层间界面不同状态下的内聚力本构模型张力位移曲线如图3所示。当0<d<1时,由(7)式可得


图3 层间界面不同状态下的内聚力本构张力位移曲线Fig.3 Cohesionmodel with initial damage
图3中,A点坐标为(δ0,Tmax),B点坐标为(δf,0),通过计算得kAB=-[Tmax/(δf-δ0)].将P(δd0,Tdmax)点带入线段AB方程中得到
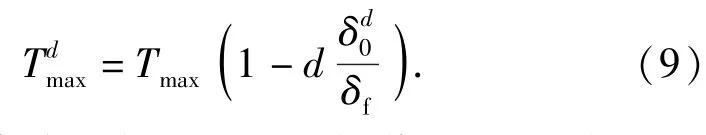
由应变等效性假设得到,损伤材料在应力σ作用下的应变响应与无损材料在有效应力σ′作用下的应变响应相同,在外力作用下受损材料的本构关系可采用无损时的形式,只要把无损材料中的Cauchy应力简单地换成有效应力即可,故得到
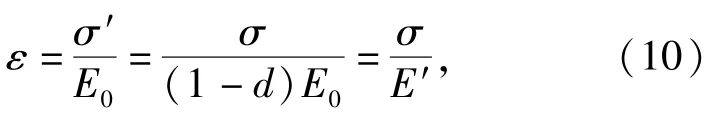
即E′=(1-d)E0,结合(1)式得到
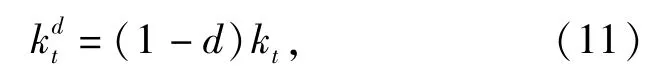
式中:t=1,2,3为层间界面3个方向刚度。
结合(8)式、(9)式和(11)式,得到当0<d<1时,内聚力数学模型为

结合初始损伤变量d的意义和图3得,当d=0时,P点将与A点重合,表明此时层间界面无损伤,由(12)式得

当d=1时,P点将与B点重合,表明此时层间界面完全损伤,由(8)式和(12)式得

由(7)式损伤因子计算表达式可知,当材料在出现损伤之后,材料的力学性能发生退化,通常用刚度弱化来描述,此时损伤后的材料刚度计算表达式为
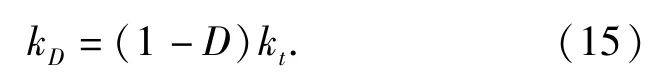
由(15)式得层间界面不同初始状态下,损伤演化时的刚度计算公式为

式中:kt为材料无损时的刚度。
2 数值模型的建立
2.1含层间效应的发射场坪数值模型
含层间效应的发射场坪数值模型如图4所示。模型从上至下依次为沥青面层、面基结合层、基层、底基层和土基。面基结合层和基层采用孤立网格偏移生成,以保证沥青面层、结合层及基层间网格的连续性;基层、底基层及土基间采用固联连接。发射场坪四周设置为对称边界条件,土基底面设置为固端约束。计算采用显式动态算法,并使用mm-tonne-s-MPa单位制。另外,在面基结合层不同位置设置动态响应观察点,便于更直观的研究面基结合层损伤分布及损伤变化。定义的观察点代表该点附近一定范围内的介质。图4中:O点为面基结合层中点,A点距O点0.5R,B点距O点1.0R,C点距O点1.5R,D点距O点2.0R,E点距O点2.5R,R为发射载荷对地作用半径。

图4 含层间效应的发射场坪数值模型Fig.4 Launching sitemathematicalmodelwith interlayer effect
面层与基层间使用SBS改性沥青作为夹层,以基于Cohesive单元的双线性内聚力模型为基础,运用(1)式~(6)式计算面基结合层界面刚度,完成面基结合层数值模型的建立,模型参数如表1[12]所示。为重点研究面基层间效应对发射场坪动态响应的影响,沥青面层、基层、底基层和土基设置为线弹性材料。各功能层材料参数和结构参数如表2[15-18]所示。

表1 面基结合层数值模型参数Tab.1 Bilinear cohesion model parameters of base-surface binding layer

表2 各功能层材料参数和结构参数Tab.2 Thematerial and structure parameters of functional layers
将发射载荷作用下发射筒底部对地载荷进行适当简化并作为输入条件,均布于发射场坪上。引入无量纲量p/p0,其中p0为对地载荷最大值。载荷曲线如图5所示。

图5 对地载荷时间曲线Fig.5 Load-time curve
2.2面基层间不同结合状态发射场坪数值模型
以含层间效应的发射场坪数值模型为基准(d=0),初始损伤d为变(12)式为控制方程,对开裂强度及界面刚度进行计算,完成层间不同结合状态发射场坪数值模型的建立。其中:初始损伤d以Δd=0.1从0增至1.0,开裂强度及界面刚度计算结果如表3所示。
表3 不同工况下开裂强度和界面刚度计算结果Tab.3 Calculated results of cracking strength and interface stiffness under differentworking conditions
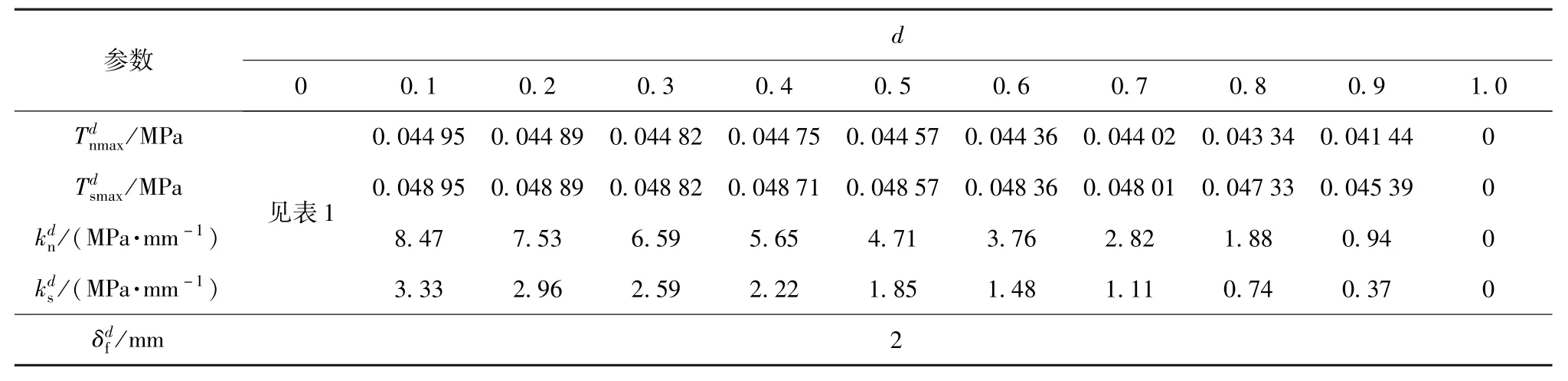
表3 不同工况下开裂强度和界面刚度计算结果Tab.3 Calculated results of cracking strength and interface stiffness under differentworking conditions
d参数0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Tdnmax/MPa Tdsmax/MPa kd n/ (MPa·mm-1)见表1 0.044 95 0.044 89 0.044 82 0.044 75 0.044 57 0.044 36 0.044 02 0.043 34 0.041 44 0 0.048 95 0.048 89 0.048 82 0.048 71 0.048 57 0.048 36 0.048 01 0.047 33 0.045 39 0 8.47 7.53 6.59 5.65 4.71 3.76 2.82 1.88 0.94 0 kd s/ (MPa·mm-1)3.33 2.96 2.59 2.22 1.85 1.48 1.11 0.74 0.37 0 δd f/ mm 2
3 结果与分析
对发射场坪动态响应的分析过程中,分别研究了未考虑层间效应的完全连续理想状态模型(图中用“LX”表示,下文简称为连续模型)和考虑层间不同结合状态的数值模型(下文简称为非连续模型)。连续模型中功能层材料参数及模型尺寸均与含层间效应的发射场坪数值模型相同,沥青面层、基层、底基层及土基间均考虑为完全连续理想状态。
3.1面基结合层损伤分布
以初始损伤d为变量表征面基层间不同结合状态,在发射载荷作用下,数值计算层间不同结合状态下面基结合层各观测点的损伤分布,计算结果如图6、图7所示。

图6 面基结合层损伤分布横向比较Fig.6 Damage distribution horizontal comparison of base-surface binding layer
由图6、图7可得:
1)横向比较面基结合层各观测点处损伤情况。随着层间结合状态的改变(初始损伤d不同),B点处介质损伤始终为1,这是因为发射载荷作用区域边界处场坪处于剪切状态,B点处介质在剪切应力作用下发生完全损伤(断裂);E点处介质损伤始终为0,这是因为在发射载荷下,面基结合层具有一定的应力分布,E点处介质所受应力极小,故该点处介质损伤始终为0.
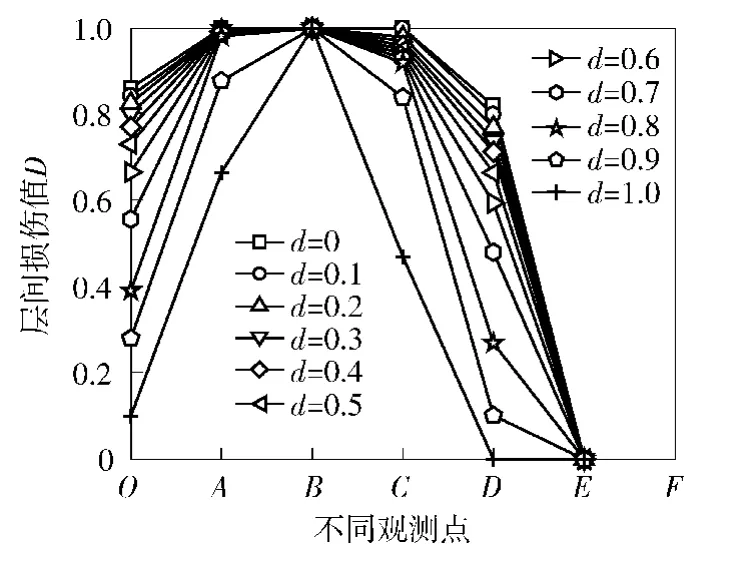
图7 面基结合层损伤分布纵向比较Fig.7 Damage distribution longitudinal comparison of base-surface binding layer
2)纵向比较面基结合层各观测点处损伤情况。当层间结合状态一定时(初始损伤d一定),沿发射载荷作用区域半径方向,面基结合层不同观测点处损伤情况表现为先增加、后减小。这是由于发射载荷作用区域边界处的面基结合层处于剪切状态,故B点处介质损伤最大(完全损伤);与B点处介质相距越远,面基结合层所受应力越小,故损伤值也将越小。
3)纵向比较面基结合层各观测点处损伤情况。当层间结合状态一定时(初始损伤d一定),A点处介质损伤大于C点处介质,O点处介质损伤大于D点处介质。这是因为A点和O点处于发射载荷作用范围内,所受应力将大于C点与D点,故A点和O点处介质损伤大于C点与D点。
4)采用横向比较与纵向比较相结合的方法研究面基结合层损伤分布。随着层间结合状态的变差(初始损伤d增加),面基结合层损伤分布表现为中间不变,两边减小的规律,即B点处介质损伤不变,O点、A点、C点、D点4点处介质损伤逐渐减小,面基结合层损伤分布纵向比较曲线变尖。这是由于随着层间结合状态的变差,面层与基层间应力传递不连续性越强,层间界面B点处介质由于完全损伤而产生的应力集中现象越明显。故随着层间结合状态的变差,O点、A点、C点、D点4点处介质所受应力变小,损伤值随之变小。此时层间界面整体损伤分布将集中在B点周边介质处。
5)采用横向比较与纵向比较相结合的方法研究面基层间界面损伤分布。当面基层间结合状态不同时,引入损伤变化因子μ,衡量不同观测点的损伤变化大小,定义为
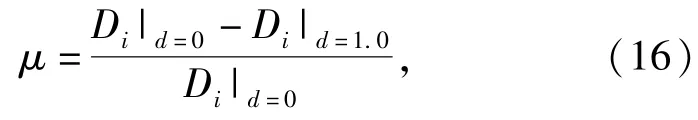
式中:D为损伤值大小;i为不同观测点。
层间不同结合状态下各观测点的损伤变化情况如表4所示。

表4 各观测点的损伤变化情况Tab.4 Damage conditions of observation points
由表4得μO>μD>μC>μA,说明当层间结合状态变差(初始损伤d为0~1.0)时,O点处介质损伤值变化最大,A点处介质损伤值变化最小。这是因为各观测点处介质的损伤值变化大小均与面基层间载荷传递的不连续性强弱有直接关系;观测点A点处介质由于与B点处介质距离较近且处于载荷作用范围内,故该点介质在d=1.0时损伤值较大,通过计算得A点处介质的损伤变化值最小。O点与D点处介质与B点处介质距离较远,故当d=1时此两点处介质损伤较小,通过计算得观测点O点处介质损伤值变化最大。
3.2位移值
面基层间不同结合状态下发射载荷作用处场坪中心点最大垂向位移和最终垂向位移如图8所示,最大水平位移和最终水平位移如图9所示。
由图8、图9可得:
1)非连续模型的位移值(垂向和水平方向)比连续模型要大,说明非连续模型的整体抗变形能力小于连续模型。
2)考虑层间结合状态的改变,当初始损伤d为0~0.9时,发射载荷作用处场坪中心点最大垂向位移和最终垂向位移变化均较小,d=0.9时的最大垂向位移是d=0时的1.033倍,d=0.9时最终垂向位移是d=0时的1.064倍。说明在发射载荷作用下、层间初始损伤d在0~0.9范围内时,场坪层间结合状态对面层垂向位移影响很小。
3)考虑层间结合状态的改变,当初始损伤d为0~0.9时,发射载荷作用处场坪中心点最大水平位移有一定变化,d=0.9时的最大水平位移是d=0时的1.315倍;最终水平位移变化较大,d=0.9时的最终水平位移是d=0时的2.762倍。说明在发射载荷作用下、层间初始损伤d在0~0.9范围内时,场坪层间结合状态对面层水平位移影响较大。这是因为层间结合状态的变差,导致场坪面层在水平方向所受约束力变小,故场坪面层水平方向自由度变大。
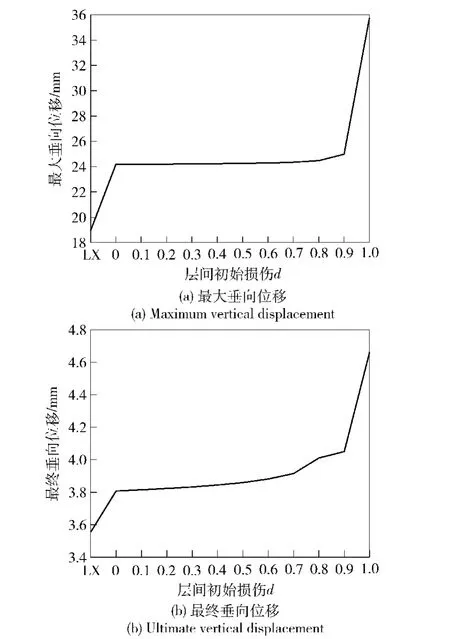
图8 发射载荷作用处场坪中心点最大、最终垂向位移Fig.8 Themaximum and ultimate vertical displacements at the central point of launching site

图9 发射载荷作用处场坪中心点最大、最终水平位移Fig.9 Themaximum and ultimate horizontal displacements at the central point of launching site
4)考虑层间结合状态的变化,当初始损伤d= 1.0时,发射载荷作用处场坪中心点位移曲线有明显的上升。d=1.0时的最大垂向位移是d=0.9时的1.43倍,d=1.0时的最终垂向位移是d=0.9时的1.15倍,d=1.0时的最大水平位移是d=0.9时的2.28倍,d=1.0时的最终水平位移是d=0.9时的2.85倍。这是因为d=1.0表示场坪面层与基层间为完全滑动,此时场坪面层在水平方向并无层间界面内聚力的约束,故场坪面层在水平方向的自由度变大。由于场坪面层水平方向位移的增加,导致场坪垂向位移的变大。
3.3面、基层层底应力
发射载荷作用下,各功能层层底最大应力作为场坪动态响应的重要指标,直接影响场坪的损伤开裂情况,进一步影响无依托发射平台的整体稳定性及发射精度。由于重点研究面基结合层对场坪动态响应的影响,故取面、基层层底中心最大应力作为研究对象,并引入无量纲量σ/σ1,其中:σ1为初始损伤d=1.0时的面、基层层底中心最大应力。层间不同结合状态下发射场坪面层层底中心最大应力如图10所示,基层层底中心最大应力如图11所示。
由图10、图11可得:
1)对于面、基层层底中心最大应力,非连续模型均比连续模型要小,特别是对于基层层底中心二者相差2.06倍。即使面基层间结合很好,初始损伤d=0时,面、基层层底中心最大应力仍然存在明显差别。这是因为非连续模型与连续模型作用机理不同。连续模型认为路面各功能层是一个完全连续的整体,层与层之间以完全连续的方式进行应力的传递与分散,因此具有较大的荷载承受能力与较强的传递并分散载荷的能力;非连续模型认为场坪各功能层是不连续体,层与层之间依靠层间粘结条件进行应力的传递,因此其传递载荷是不连续的,分散载荷的能力较差。事实上,发射场坪结构是由不同材料层组成,层与层间结合状态再好,依旧为不连续体。因此在研究发射载荷作用下场坪动态响应时,采用非连续模型将更加合理。
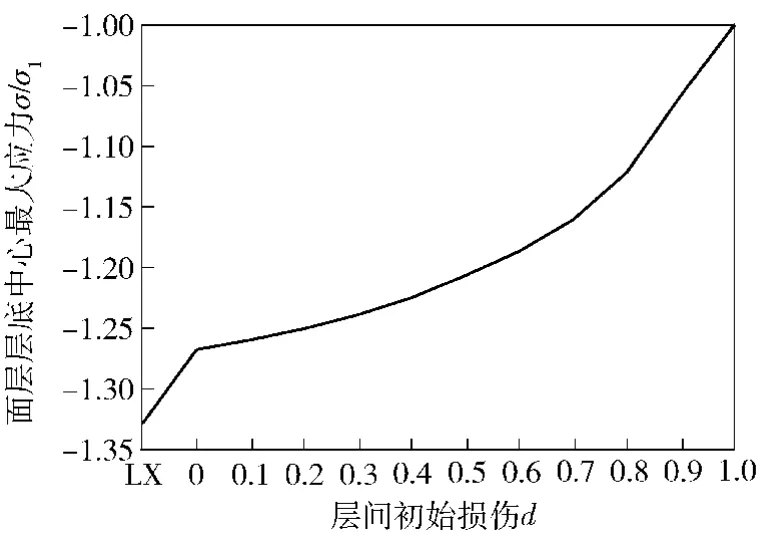
图10 面层层底中心最大应力Fig.10 Themaximum stress of surface layer center-bottom point

图11 基层层底中心最大应力Fig.11 Themaximum stress of base layer center-bottom point
2)当采用非连续模型时,面层层底中心应力到达最大时为负,说明此时该点处介质处于受压状态;基层层底中心应力到达最大值时为正,说明此时该点处介质处于受拉状态。此现象与非连续模型的作用机理有直接关系,且进一步佐证了非连续模型传递载荷的不连续性。
3)随着面基层间结合状态的变差(初始损伤d 为0~1.0),面层层底中心最大应力和基层层底中心最大应力均变小。d=0时面层层底中心最大应力是d=1.0时的1.27倍,而d=0时基层层底中心最大应力是d=1.0时的1.15倍。说明在发射载荷作用下,面基层间结合状态的不同对面、基层层底中心最大应力有一定影响。
4 结论
1)当场坪层间结合状态一定时(初始损伤d一定),沿发射载荷作用区域半径方向,面基结合层不同观测点处损伤表现为先增加、后减小,且观测点A点处介质损伤大于观测点C点处介质,观测点O点处介质损伤大于观测点D点处介质。因此面基结合层不同观测点处介质损伤大小排序为DB>DA>DC>DO>DD>DE.
2)随着面基层间界面初始状态的变差(初始损伤d为0~1.0),层间界面整体损伤分布表现为中间不变、两边变小;观测点B点处介质损伤始终为1,观测点E处介质损伤始终为0,观测点O点处介质损伤值变化最大,观测点A点处介质损伤值变化最小,层间界面各观测点处介质损伤变化大小排序为μO>μD>μC>μA>μB=μE.
3)发射载荷作用下,两种不同类型的场坪模型位移值为:考虑层间效应的发射场坪数值模型大于未考虑层间结合的完全连续理想状态模型;面、基层层底中心最大应力为考虑层间效应的发射场坪数值模型小于未考虑层间结合的完全连续理想状态模型。说明考虑层间效应的发射场坪数值模型虽然在整体抗变形能力、层间传递载荷能力和分散载荷能力上,均比未考虑层间结合的完全连续理想状态模型差,但更接近无依托发射场坪实际状态。
4)随着层间结合状态的变差,场坪面层垂向位移和水平位移均产生不同程度的变大;当面基层间界面初始损伤d为0~0.9时,层间不同结合状态对场坪面层垂向位移影响很小,对水平位移有一定影响。当面基层间界面初始损伤d=1.0时,层间结合状态对场坪面层垂向位移和水平位移均产生较大影响。
5)随着层间结合状态的变差(初始损伤d为0~1.0),面、基层层底中心最大应力均变小;面基层间不同结合状态对二者数值影响大小排序为场坪面层层底中心最大应力大于基层层底中心最大应力。
(References)
[1]Spearman M L.Innovation in aerodynamic design features of soviet missiles,NASA 20080014230[R].Virginia:American Institute of Aeronautics and Astronautics,2008.
[2]Seow Y W.Survivability enhancement in a combat environment,ADA429875[R].CA:Naval Postgraduate School Monterey,2004.
[3]严二虎,沈金安.半刚性基层与沥青层之间界面条件对结构性能的影响[J].公路交通科技,2004,21(1):38-41. YAN Er-hu,SHEN Jin-an.Structural influence of boundary condition between asphalt layer and semi-rigid base[J].Journal of Highway and Transportation Research and Development,2004,21(1):38-41.(in Chinese)
[4]薛亮,张维刚,梁鸿颉.考虑层间不同状态的沥青路面力学响应分析[J].沈阳建筑大学学报:自然科学版,2006,22(4):575-578. XUE Liang,ZHANGWei-gang,LIANG Hong-jie.The mechanical response analysis of asphalt pavement in different interface condition between layers[J].Journal of Shenyang Jianzhu University:Natural Science,2006,22(4):575-578.(in Chinese)
[5]关昌余,王哲人.路面结构层间结合状态的研究[J].中国公路学报,1989,2(1):70-80. GUAN Chang-yu,WANG Zhe-ren.Analysis interface bond of the pavement structures[J].China Journal of Highway and Transport,1989,2(1):70-80.(in Chinese)
[6]颜可珍,江毅,黄立葵,等.层间接触对沥青加铺层性能的影响[J].湖南大学学报:自然科学版,2009,36(5):11-15. YAN Ke-zhen,JIANG Yi,HUANG Li-kui,et al.Effect of bond condition on overlay performance[J].Journal of Hunan University:Natural Sciences,2009,36(5):11-15.(in Chinese)
[7]Goodman R E,Taylor R L,Brekke T L.A model for themechanics of jointed rock[J].The Soil Mechanics and Foundations Division,1968,94(3):637-658.
[8]Dempsey B J.Development and performance of interlayer stress absorbing composite in asphalt concrete overlays[J].Transportation Research Record,2002,1809(1):175-183.
[9]黄宝涛,廖公云,张静芳.半刚性基层沥青路面层间接触临界状态值的计算方法[J].东南大学学报:自然科学版,2007,37(4):666-670. HUANG Bao-tao,LIAO Gong-yun,ZHANG Jing-fang.Analytical method of interlayer contact fettle in semi-rigid base bituminous pavement[J].Journal of Southeast University:Natural Science E-dition,2007,37(4):666-670.(in Chinese)
[10]艾长发,邱延峻,毛成,等.考虑层间状态的沥青路面温度与荷载耦合行为分析[J].土木工程学报,2007,40(12):99-104. AIChang-fa,QIU Yan-jun,MAO Cheng,et al.Simulation of the temperature load coupling effect on asphalt pavement considering interlayer conditions[J].China Civil Engineering Journal,2007,40(12):99-104.(in Chinese)
[11]赵炜诚,许志鸿,黄文.混凝土面层与贫混凝土基层的层间作用对荷载应力和弯沉的影响[J].中国公路学报,2003,16(4):9-15. ZHAOWei-cheng,XU Zhi-hong,HUANG Wen.Influence of load stress and deflection on interfacial interaction between portland concrete pavement and lean concrete base[J].China Journal of Highway and Transport,2003,16(4):9-15.(in Chinese)
[12]李彦伟,穆柯,石鑫,等.基面层间接触状态对沥青路面力学响应影响[J].长安大学学报:自然科学版,2014,34(2):38-44. LIYan-wei,MU Ke,SHI Xin,et al.Impact of base-surface contact condition on mechanical response of asphalt pavement [J].Journal of Chang'an University:Natural Science Edition,2014,34(2):38-44.(in Chinese)
[13]张东,黄晓明,赵永利.基于内聚力模型的沥青混合料劈裂试验模拟[J].东南大学学报:自然科学版,2010,40(6):1276-1281. ZHANG Dong,HUANG Xiao-ming,ZHAO Yong-li.Simulation of indirect tension test of asphalt ixtures based on cohesive zone model[J].Journal of Southeast University:Natural Science Edition,2010,40(6):1276-1281.(in Chinese)
[14]Song SH,Paulino G H,ButtlarW G.A bilinear cohesive zone model tailored for fracture of asphalt concrete considering visco-elastic bulkmaterial[J].Journal of Engineering Fracture Mechanics,2006,73(18):2829-2848.
[15]吴超凡.贫混凝土基层混凝土路面层间作用机理及处治技术研究[D].西安:长安大学,2009. WU Chao-fan.Research on actionmechanism and handling technology between cement concrete pavement and lean cement concrete base[D].Xi'an:Chang'an University,2009.(in Chinese)
[16]王金昌,朱向荣.软土地基上沥青混凝土路面动力分析[J].公路,2004(3):6-11. WANG Jin-chang,ZHU Xiang-rong.Dynamic analysis of asphalt concrete pavement on soft clay ground[J].Highway,2004(3):6-11.(in Chinese)
[17]左志国,曹高尚,宋红领.Thiopave改性沥青路面力学响应研究[J].青岛理工大学学报,2011,32(6):26-29. ZUO Zhi-guo,CAO Gao-shang,SONG Hong-ling.Research on mechanical response of Thiopavemodified bituminous pavements [J].Journal of Qingdao Technological University,2011,32(6):26-29.(in Chinese)
[18]柳志军,刘春荣,胡朋,等.土基回弹模量合理取值试验研究[J].重庆交通学院学报,2006,25(3):62-64. LIU Zhi-jun,LIU Chun-rong,HU Peng,etal.Experiment study on reasonable evaluation of rebound modulis of subgrade[J]. Journal of Chongqing Jiaotong College,2006,25(3):62-64. (in Chinese)
Research on Dynam ic Response of Launching Site Based on Different Interlayer Binding States
ZHOU Xiao-he1,MA Da-wei2,ZHU Zhong-ling2,LIAO Xuan-ping1,JU Xiao-jie1
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China;2.China Adacemy of Launch Vehicle Technology,Beijing 100076,China)
To obtain the dynamic response of the launching site under the different binding states of base and surface layers,an interlayer binding mathematicalmodel of base and surface layers is established based on bilinear cohesion constitutive of cohesive element.A cohesionmathematicalmodel under different binding states of base and surface layers is established by introducing the initial damage variable and using the strain equivalence hypothesis.A numerical model of launching site under different binding states of base and surface layer is built based on the numericalmodelwith interlayer effect,the distribution and evolution of damage on base-surface layer interface of the launching site below the bottom of launch canister are analyzed,and the dynamic response of the launching site under different binding states of base and surface layer is researched.The result shows that,when the base-surface layer binding state remains constant,the interface damage is themost serious in the base layer where the boundary is forced by the load applied by the bottom of the launch canister,and the interface damage of the base layer firstly increases and then decreases along the radius direction of the load area.When the binding stateof base and surface layer getsworse,the interface damage of the base layer is invariant in themiddle and decrease on both sides along the radius direction of the load area,the vertical and horizontal displacements of the launching site surface get larger in different degrees,and themaximum stresses of the surface and base layers center-bottom points get smaller.
ordnance science and technology;launching site;interlayer interface;cohesion constitutive;initial damage;dynamic response
TJ768.1
A
1000-1093(2015)12-2269-09
10.3969/j.issn.1000-1093.2015.12.009
2015-02-04
国家自然科学基金项目(51303081);江苏省自然科学基金项目(BK20130761)
周晓和(1988—),男,博士研究生。E-mail:xiaohezhou@126.com;马大为(1953—),男,教授,博士生导师。E-mail:ma-dawei@mail.njust.edu.cn
