虚位技术对相控阵雷达导引头制导性能的影响

鲁天宇，尹健，杜肖，夏群利（1.北京理工大学机电学院，北京100081；2.空军装备研究院装备总体论证研究所，北京100076；.北京理工大学宇航学院，北京100081）

虚位技术对相控阵雷达导引头制导性能的影响

鲁天宇1，3，尹健1，2，杜肖3，夏群利3
（1.北京理工大学机电学院，北京100081；2.空军装备研究院装备总体论证研究所，北京100076；3.北京理工大学宇航学院，北京100081）

为了研究相控阵雷达导引头（PARS）采用虚位技术后对导弹制导性能的影响，根据天线单元置相原理，分析了波束指向误差斜率（BSES）产生的原因，推导了弹体扰动下含有BSES的视线角速率输出传递函数，对其幅值及相角变化规律进行了分析。同时，根据波束空间指向角度关系，建立了BSES寄生回路模型，利用劳斯判据研究了不同虚位数对寄生回路稳定边界的影响。在雷达典型噪声输入条件下，利用参数无量纲化方法研究了不同虚位数对脱靶量的影响。研究表明：PARS采用虚位技术后将产生BSES，虚位数越大，BSES越大，在相同条件下寄生回路越容易失稳，所带来的脱靶量越大，接收机噪声比目标闪烁噪声对脱靶量的影响更大。因此需要根据不同的虚位数进行不同指向区间的误差标定，降低BSES，提高导弹末制导精度。

飞行器控制、导航技术；相控阵雷达导引头；虚位技术；波束指向误差斜率；寄生回路

0　引言

相控阵雷达导引头（PARS）作为一种新兴制导体制，具有机械扫描雷达导引头所不能实现的快速性、灵活性，而且抗干扰及自适应能力更强，可靠性更高[1-2]，现已成为各军事强国研制、升级空空导弹争先发展的领域[3-4]。PARS波束扫描过程存在波束跃度，将造成波束的离散扫描[5-6]。数字移相器所能实现的最小移相值和其位数有关，然而现有水平很难做出高位数移相器。为了降低波束跃度，使天线波束扫描接近机械式连续转动天线的情况，需要增加移相器的位数。为节省数字移相器的位数，同时保证较小的波束跃度，一般都采用虚位技术[7]，但是采用虚位技术又会带来其他问题。

国内外文献关于采用虚位技术所带来的问题主要集中在产生量化副瓣[7]及其解决办法[8-10]上，而几乎没有涉及虚位带来的波束指向误差斜率（BSES）及由其产生的制导系统寄生回路问题。Nesline等[11]提出了雷达导引头天线罩斜率产生制导系统的寄生回路，研究了其对制导系统性能的影响；Janice等[12]提出了基于全捷联体制的天线罩是PARS急需解决的关键技术；杜运理等[13]提出了平台导引头隔离度相位滞后对寄生回路稳定性的影响；李富贵等[14]提出了全捷联导引头刻度尺偏差带来的隔离度寄生回路问题及其辨识校正方法；宋韬等[15]建立了干扰力矩引起的隔离度完整模型，并研究了其对寄生回路稳定性的影响。

本文基于相控阵导引头全捷联制导体制，分析了虚位技术产生BSES的原因，推导了弹体扰动下视线角速率输出传递函数，对其频率特性进行了分析，同时建立了BSES寄生回路模型，研究了不同虚位数对寄生回路稳定边界的影响，以及在目标闪烁噪声、接收机噪声等雷达典型噪声输入条件下，不同虚位数对应的末制导脱靶量。所得结论可为PARS移相器虚位数的选取及误差标定提供重要的参考价值。

1　波束指向误差斜率产生的主要原因

1.1虚位技术

为节省移相器位数，同时保证较小的波束跃度，使波束转动达到接近连续扫描的效果，需要在已有的实位移相器的基础上增加虚位数，图1所示为实位数m=5，采用虚位数b=4的移相器天线单元置相原理图[7]。

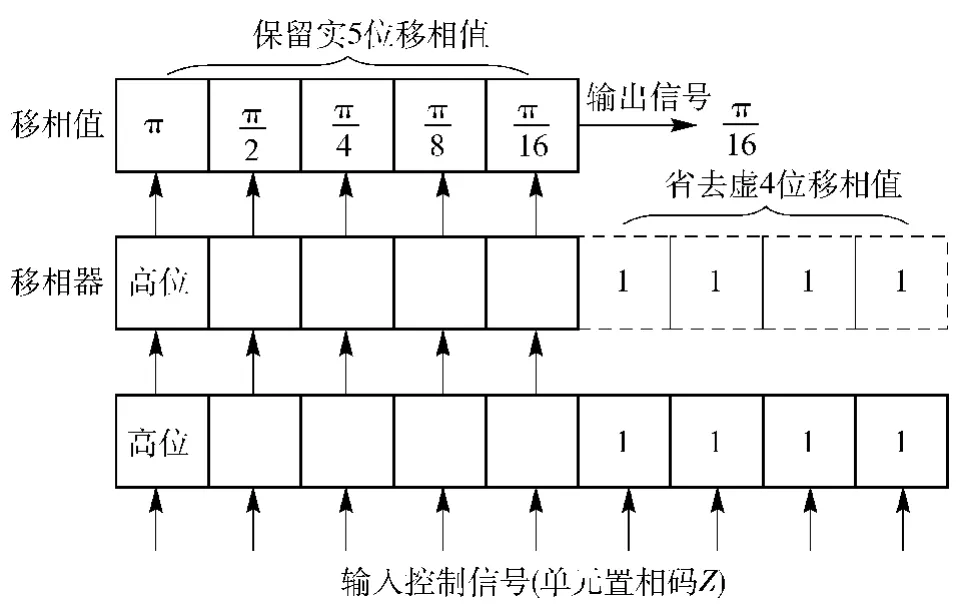
图1　天线单元置相原理Fig.1　Principle of antenna element shift phase

在进行各辐射单元置相时，先按照K=b+m= 9位移相器计算最小移相值ΔφBmin=2π/2K，同时确定波束控制码P，则第i个单元的单元置相码Z= iP，置相码以二进制数表示，省去低 4位，取Z-mod（Z，2b）作为实际置相码，其中，mod（Z，2b）表示Z除以2b的余数。

图2给出了单元数为N=32，i=0，…，31，波控码P=18，采用上述移相器实位5位，虚位4位的虚位技术可以得到理论单元移相值、虚位带来的虚位移相值、实位带来的实位移相值、实际总移相值，图中阴影部分表示采用虚位技术后带来的单元移相误差，单元移相误差将产生波束指向误差。同时，由实际总移向值曲线可以看出，子阵单元间也存在扫描。

图2　采用虚位技术的单元移相值Fig.2　Unit phase shifting by phantom-bit technology

表1给出了天线单元数N=32，移相器实位m=5，虚位数b=3，4，5时，实位扫描一个波束跃度时的最大波束指向误差。由表1可以看出，虚位数越大，波束指向误差越大，在波束扫描过程中会出现正负指向误差。

表1　不同虚位数带来的波束指向误差Tab.1　Boresight errors due to different phantom-bit numbers

1.2波束指向误差斜率

采用虚位技术后，将产生波束指向误差，图3给出了波束扫描过程中理论波束指向与实际波束指向关系。其中：θBC为理论波束指向值，θB为实际波束指向值，Δ为波束指向误差。

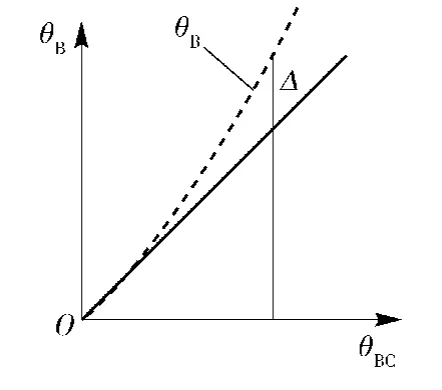
图3　波束指向关系Fig.3　Beam angle direction

建立理论波束指向与实际波束指向关系：

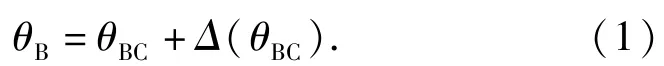
对（1）式求导得

当Δ=ct时，R=∂Δ（θBC）/∂θBC=0，说明常值波束指向误差不影响PARS的制导性能。

由前面分析可知，虚位技术带来的波束指向误差Δ不为常值，当波束扫描时，取波束指向误差最大值处的误差斜率作为整个波束扫描范围内的误差斜率，考虑到实位第一跳θBC=3.58°，计算可得虚位数b=3，4，5时，BSES为R3=±0.01，R4=±0.03，R5=±0.05.

2　弹体扰动视线角速率输出

建立如图4所示含有BSES的PARS跟踪回路，其中：k为前向通道增益；kg1、kg2为刻度尺系数。本文中，令kg1=kg2=1，使系统无刻度尺偏差，~θBC到θB为包含BSES的非线性开环控制过程。

建立包含弹体运动的视线角速率输出函数：

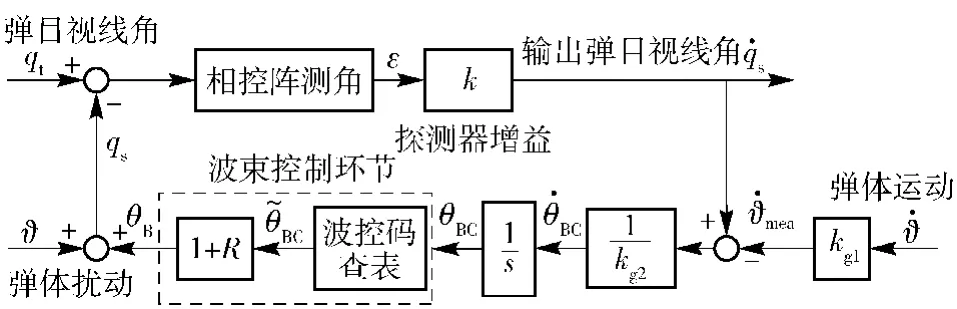
图4　视线角速率提取模型Fig.4　Line-of-sight rate extraction model

1）由弹体扰动引起的弹目视线角速率输出

2）由弹体角速率陀螺反馈引起的弹目视线角速率输出

（3）式加（4）式得弹体运动引起的弹目视线角速率输出为

由（5）式可以看出，只有当波束指向角误差斜率R为0时，弹体运动引起的弹目视线角速率为0.

图5给出了不同虚位数条件下的视线角速率输出伯德图。由图5可以看出，随着频率的增加，弹体扰动引起的视线角速率幅值减小，虚位数越大，弹目视线角速率幅值越大，对制导系统的影响越严重。虚位数对相特性几乎没有影响。

图5　不同虚位数下视线角速率输出伯德图Fig.5　Bode diagrams of line-of-sight rate output in the case of different phantom-bit numbers

3　波束指向误差斜率寄生回路分析

3.1模型的建立

由于BSES的存在，当弹体运动时将产生附加的视线角速率，如（5）式所示，该附加视线角速率作为导引头输出的一部分，经过制导滤波器、驾驶仪形成额外制导指令控制弹体运动，以此反复形成了制导系统的寄生内回路。

图6给出了导弹和目标在纵向平面的相对几何关系。其中：弹目视线指向目标，为弹体姿态角，qt为弹目视线角，qs为导引头输出理论波束指向相对惯性空间夹角，θBC为理论波束指向角，θB为实际波束指向角，ε为理论失调角，~ε为实际失调角，~ε由单脉冲测角机构测量得到。

图6　弹目相对关系Fig.6　Engagement geometry betweenmissile and target

为简化研究，不失一般性，导弹制导系统采用4阶多项式来表示，其中制导滤波器为一阶模型，自动驾驶仪为3阶模型，Tg为制导时间常数，Tα为攻角时间常数，N为有效导航比，Vc为弹目相对速度，Vm为导弹飞行速度。由图6可得相应的数学模型：

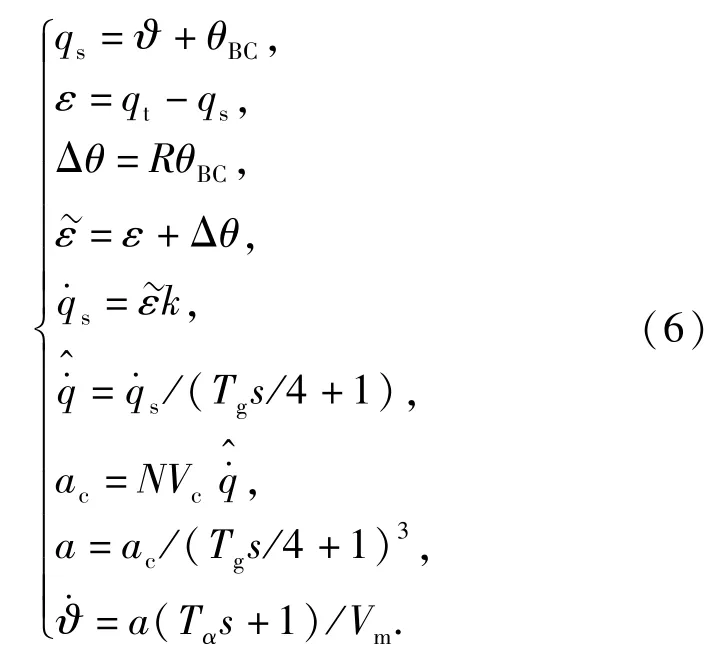
由（6）式可知，考虑BSES后，比例导引制导回路由9个方程组成，同时有9个未知数：因此上式封闭可解，可得含有BSES的比例导引制导回路框图如图7所示。

（3）借助多渠道获取多种资源，解决身边一些的生物学与环境科学问题，拟定“认识酸雨危害 保护桂林绿水青山”行动计划。

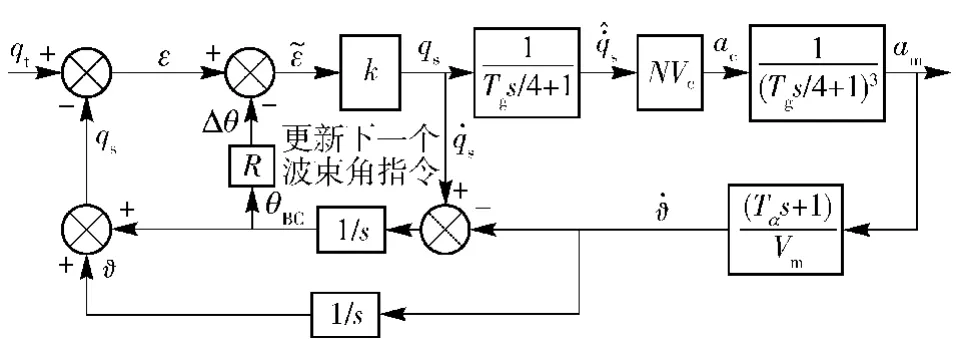
图7　考虑BSES的制导回路框图Fig.7　Block diagram of guidance loop with BSES

根据图7可得闭环传递函数为

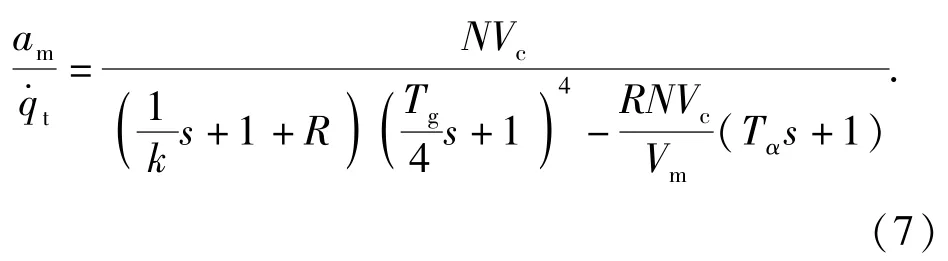
由前面分析可知，虚位技术带来的 BSES，即|R|≪1，故（7）式可简化为

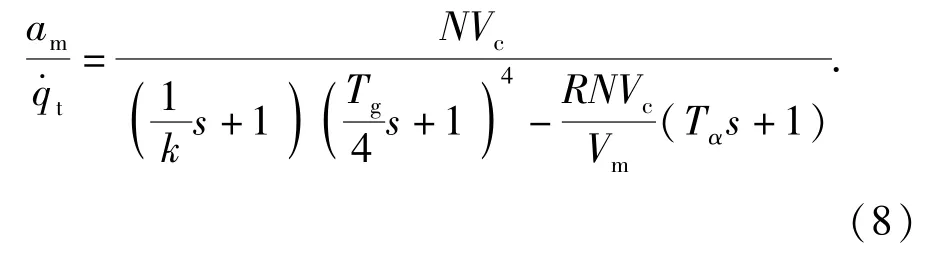
由（8）式传递函数得闭环阶跃响应曲线如图8所示。由图8可以看出，BSES为0时，系统有稳态输出。当含有虚位波控环节的制导回路为正反馈时，随着虚位数增加，超调越大，过载输出稳态误差变大，系统越不稳定；当含有虚位波控环节的制导回路为负反馈时，随着虚位数增加，过载输出稳态误差增大，快速性降低。

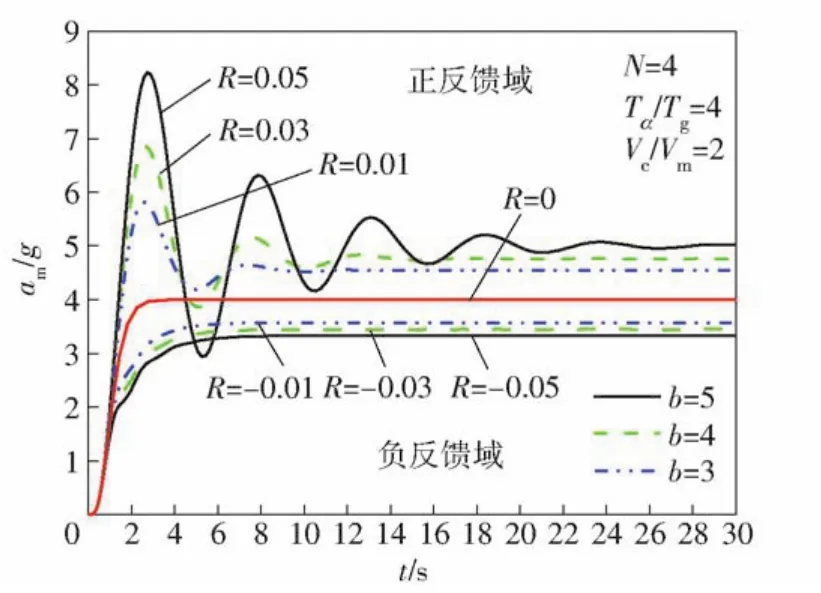
图8　过载响应曲线Fig.8　Curves of overload response

3.2稳定性分析

针对中远距空空导弹制导过程，初始弹目相距较远，制导回路的前向增益很小，分析BSES对制导系统的稳定性影响时，可忽略制导外回路，单独对BSES寄生回路进行分析。

（8）式的稳定性决定了寄生回路的稳定性，寄生回路闭环传函特征方程为法，令

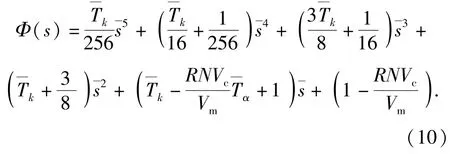
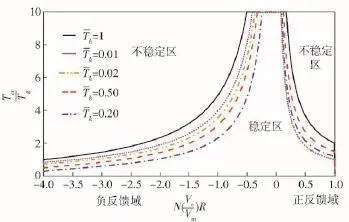
图9　BSES寄生回路稳定边界Fig.9　Stable boundary of BSES parasitic loop

3.3制导精度分析

对于PARS制导系统而言，目标闪烁噪声和接收机噪声是其主要误差源[16]。在含有BSES寄生回路的制导系统内引入上述两种噪声，将影响末制导精度，带来脱靶量。其中：目标闪烁噪声功率谱密度为ΦGN，带来的脱靶量记为σGN，接收机噪声功率谱密度为ΦRN，带来的脱靶量记为 σRN，R0为参考距离，TF为末制导时间。建立由接收机热噪声和目标闪烁噪声带来的比例导引制导回路伴随系统如图10所示。

图10　噪声输入下的制导回路伴随模型Fig.10　Adjointmodel of guidance system with noise input

为了减少变量数，利用时间尺度无量纲变换，令

经过推导可得目标闪烁噪声和接收机噪声带来的时并处理得间尺度无量纲化后的脱靶量表达式分别为：

在制导外回路中引入BSES寄生回路，可使制导系统失稳并输出错误的制导信号，导致脱靶量增大。图11和图12分别给出了目标闪烁噪声和接收机噪声作用下无量纲脱靶量随不同参数的变化曲线。仍取典型空空导弹参数进行分析，相控阵导引头前向通道增益取k=13，使导引头满足2 Hz频带的快速性。由仿真结果图11（a）和图11（b）可看出，当Tα/Tg不变时，无量纲脱靶量随着虚位数的增加而增大。当BSES为正值时，无量纲脱靶量随其增大而迅速增大，对虚位数的变化很敏感，对同一BSES，Tα/Tg越大，无量纲脱靶量越大，Tα/Tg越大，在临界稳定点处所允许的无量纲脱靶量越小，这与前面分析的寄生回路稳定边界随Tα/Tg的变化趋势一致；当BSES为负值，且保证制导系统稳定时，虚位数及Tα/Tg对临界稳定点处的无量纲脱靶量影响很小，一旦超过临界点，无量纲脱靶量将急剧增大。由图12（b）仿真结果可看出，虚位数越大，对Tα/Tg的变化越敏感。虚位数取3时，无量纲脱靶量趋于一条直线，受Tα/Tg的变化影响不大。对比图11、图12可看出，在相同条件下，接收机噪声引起的无量纲脱靶量比闪烁噪声大很多，且对虚位数的变化更敏感。

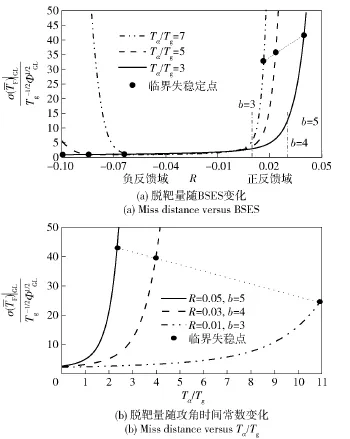
图11　闪烁噪声引起的无量纲脱靶量曲线Fig.11　Curves of dimensionlessmiss distance due to glint noise

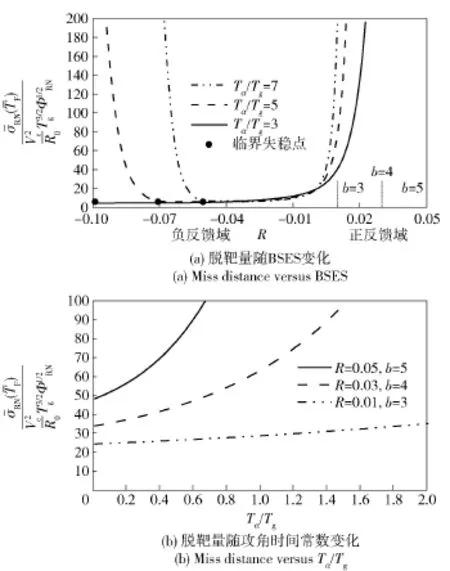
图12　接收机噪声引起的无量纲脱靶量曲线Fig.12　Curves of dimensionlessmiss distance due to receiver noise

4　结论

PARS为了获得更小的波束跃度，起到连续扫描的效果，需要引入虚位技术。本文分析了虚位技术产生BSES的原因，建立了BSES寄生回路模型及含有不同噪声输入下的制导回路模型，研究了不同虚位数对寄生回路稳定性及末制导脱靶量的影响，所得结论如下：

1）PARS采用虚位技术将产生BSES，虚位数越大，BSES越大，且会形成容易使系统失稳的正反馈回路。

2）采用全捷联形式的相控阵导引头，弹体扰动将会带来额外的视线角速率输出，虚位数越大，额外输出的视线角速率幅值越大。

3）对于中远距空空导弹，弹目距离较远时BSES寄生回路稳定域大小与Tα/Tg、R、N、Vc/Vm、1/kTg等参数有关，通过仿真可知，虚位数越大，即BSES绝对值越大，稳定边界越小，系统越容易失稳。

4）典型雷达噪声输入下，虚位数越大，无量纲脱靶量越大，接收机噪声比闪烁噪声对末制导精度的影响更大。正BSES比负BSES引起的脱靶量变化更迅速。

以上结论可以为PARS的设计，虚位数的选取及导弹制导系统参数的选择提供理论支撑。

（References）

[1]樊会涛，杨军，朱学平.相控阵雷达导引头波束稳定技术研究[J].航空学报，2013，34（2）：387-392. FAN Hui-tao，YANG Jun，ZHU Xue-ping.Research on beam stable technology of phased array radar seeker[J].Acta Aeronautica et Astronautica Sincia，2013，34（2）：387-392.（in Chinese）

[2]王琪，付书堂.相控阵雷达导引头捷联波束稳定算法研究[J].航空兵器，2011（6）：3-5. WANG Qi，FU Shu-tang.Study on strapdown beam steadying algorithm of phased array radar seeker[J].Aero Weaponry，2011（6）：3-5.（in Chinese）

[3]赵鸿燕.相控阵雷达导引头技术发展现状 [J].飞航导弹，2011，21（8）：78-82. ZHAO Hong-yan.Present situation of phase-array-radar seeker [J].Aviation Missile，2011，21（8）：78-82.（in Chinese）

[4]唐怀民，魏飞鸣，宋柯，等.相控阵雷达导引头技术发展现状分析[J].制导与引信，2014，35（3）：6-10. TANG Huai-min，WEI Fei-ming，SONG Ke，et al.Analysis on technology development status quo of phased arrary radar seeker [J].Guidance and Fuze，2014，35（3）：6-10.（in Chinese）

[5]沈文辉，周希郎，宫新保.提高相控阵天线波束指向精度的方法[J].上海交通大学学报，2004，38（2）：233-235. SHENWen-hui，ZHOU Xi-lang，GONG Xin-bao.Method for improving the beam-steering accuracy of phased array antenna[J]. Journal of Shanghai Jiao Tong University，2004，38（2）：233-235.（in Chinese）

[6]王嘉鑫，林德福，祁载康，等.全捷联相控阵雷达导引头隔离度寄生回路研究[J].北京理工大学学报，2013，33（11）：1124-1129. WANG Jia-xin，LIN De-fu，QIZai-kang，et al.Study on disturbance rejection rate parasitical loop of strapdown phased array radar seeker[J].Transactions of Beijing Institute of Technology，2013，33（11）：1124-1129.（in Chinese）

[7]张光义.相控阵雷达原理[M].北京：国防工业出版社，2009. ZHANG Guang-yi.Principle of phased array radar[M].Beijing：National Defense Industry Press，2009.（in Chinese）

[8]王峰，王晟达，马健，等.量化副瓣消除方法的研究 [J].微计算机信息，2008，24（11）：242-244. WANG Feng，WANG Sheng-da，MA Jian，etal.Theway ofeliminating the quantization sidelobes[J].Microcomputer Information，2008，24（11）：242-244.（in Chinese）

[9]张文琪，刘伟伟.移相器位数对相控阵天线指向精度的影响[J].现代导航，2013（2）：153-156. ZHANGWen-qi，LIUWei-wei.Effect of digital phase shifterwith different digits on accuracy of antenna beam direction[J].Modern Navigation，2013（2）：153-156.（in Chinese）

[10]Smith M S，Guo Y C.Comparison ofmethods for randomizing phase quantization errors in phased array[J].IEEE Transactions on Antennas and Propagation，1983，32（6）：821-828.

[11]Nesline FW，Zarchan P.Radome induced miss distance in aerodynamically controlled homing missiles[C]∥AIAA Guidance and Control Conference.New York，US：AIAA，1984：712-717.

[12]Janice CR，James H M，Joel PB，etal.The past，present，and future of electronically-steerable phased arrays in defense application[C]∥IEEE Aerospace Conference.Big Sky，MT，US：IEEE，2008：1011-1020.

[13]杜运理，夏群利，祁载康.导引头隔离度相位滞后对寄生回路稳定性影响研究[J].兵工学报，2011，32（1）：28-32. DU Yun-li，XIA Qun-li，QI Zai-kang.Research on effect of seeker disturbance rejection ratewith phase lag on stability of parasitical loop[J].Acta Armamentarii，2011，32（1）：28-32. （in Chinese）

[14]李富贵，夏群利，祁载康.全捷联导引头寄生回路影响与辨识校正[J].系统工程与电子技术，2013，35（8）：1717-1722. LIFu-gui，XIA Qun-li，QIZai-kang.Effect of parasitic loop on strap-down seeker and compensated with identification method [J].Systems Engineering and Electronics，2013，35（8）：1717-1722.（in Chinese）

[15]宋韬，林德福，王江.平台导引头隔离度对导弹制导系统影响[J].哈尔滨工程大学学报，2013，34（10）：1234-1241. SONG Tao，LIN De-fu，WANG Jiang.Influence of seeker disturbance rejection rate on missile guidance system[J].Journal of Harbin Engineering University，2013，34（10）：1234-1241. （in Chinese）

[16]Zarchan P.Tactiacl and strategic missile guidance[M].5th ed. Virginia：AIAA Inc，2007.

Effect of Phantom-bit Technology on Guidance Performance of Phased Array Radar Seeker

LU Tian-yu1，YIN Jian2，DU Xiao1，XIA Qun-li1
（1.School of Mechatronical Engineering，Beijing Institute of Technology，Beijing 100081，China；2.General Demonstration Institute，Equipment Academy of Air Force，Beijing 100076，China；3.School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China）

To study the effectof phantom-bit technology for phased array radar seeker（PARS）onmissile guidance system，the cause of boresight error slope（BSES）is discussed according to the principle of antenna element shift phase，the transfer function of line-of-sight rate containing BSES is derived under the disturbance ofmissile body，and the change rules of amplitude and phase angle are analyzed.A model of BSES parasitic loop is established based on the pointing angle of beam space，and the effect of phantom bit number（PBN）on the stability boundary of parasitic loop is studied with Routh criteria.Under the condition of the typical radar noise input，the dimensionless and adjointmethods are used to research the influence of PBN onmiss distance.The result shows that phantom-bit technology of PARS leads to BSES；the larger the PBN is，the bigger the BSES is，the easier the parasitic loop loses its satbility，and the larger themiss distance is.The receiver noise has a greater effect on miss distance compared to target glint noise under the same condition.Therefore an error calibration method，which is used to calibrate the error among different beam angle directions according to different PBNs，needs to be studied to reduceBSES and improve the accuracy ofmissile terminal guidance.

control and navigation technology of aerocraft；phased array radar seeker；phantom-bit technology；boresight error slope；parasitic loop

TJ765.3

A

1000-1093（2015）12-2262-07

10.3969/j.issn.1000-1093.2015.12.008

2014-12-03

上海航天科技创新基金项目（SAST201302）

鲁天宇（1987—），男，博士研究生。E-mail：lutianyu1987@126.com；尹健（1961—），男，研究员，博士生导师。E-mail：yin160@sohu.com