冲击波作用下炸药安全性QMU评估

花 成，张盛国，高大元

（1.中国工程物理研究院化工材料研究所，四川 绵阳 621900；2.中国工程物理研究院安全弹药研发中心，四川 绵阳 621900；3.第二炮兵驻中国工程物理研究院代表室，四川 绵阳 621900）

引 言

裕度和不确定度的量化（quantification of margins and uncertainties，QMU）方法是美国LNNL、LANL和Sandia三大国家实验室用于武器有效性评估的新方法。该方法将性能、阈值和不确定度三者统一起来，用以评价复杂武器系统、子系统及部组件的性能是否达到其安全可靠工作所要求的阈值和裕度，以及评价结果的可信程度。QMU裕度和不确定度量化评估是对武器使用有效性评价结果可信程度的一种数学表述形式，QMU评估的主要途径是量化特定性能参数的不确定性和安全性裕量，已广泛应用于复杂武器系统可靠性的QMU评估［1－6］。但是，QMU 目前主要用于复杂系统可靠性评估研究，对炸药、火工品安全性的裕度和不确定度量化QMU评估模型及评估方法的报道较少。不同领域的安全性试验，均可体现为冲击波压力、落高、电压、电流、温度等刺激量与响应之间的关系。冲击波作用下炸药安全性一般采用大隔板、小隔板试验进行测试［7－8］。

本研究通过量化炸药安全性参量的不确定区间和安全性裕量，研究了以冲击波隔板试验中隔板厚度、即入射至被炸药冲击波压力作为单一刺激量时进行炸药冲击波安全性QMU评估的方法，以期为其他安全性QMU评估提供参考。

1 炸药安全性QMU评估模型

QMU 的数学表达式为［9－12］：

式中：Q为炸药安全性的可信度比值；M为确保炸药安全性要求的性能值与系统可能出现的安全性阈值之间的差值，即裕量；U为炸药安全性裕量的不确定度；X0为炸药安全性设计值；Xth为炸药安全性客观要求的阈值，即最低性能值。

当Q＞1时，炸药安全性可靠；当Q＜1时，炸药安全性不可靠。炸药安全性QMU评估关键要素见图1。

图1 炸药安全性QMU评估的关键要素Fig.1 Key factors of QMU evaluation for explosive safety

当Q＞1满足QMU要求以及Q＜1不满足QMU要求时，炸药安全性设计值范围D与确保炸药安全性要求的安全性范围S之间的关系见图2。当炸药安全性设计值范围D∈S时，Q＞1；反之Q＜1。图2中，横坐标x代表刺激量，P代表响应水平。

图2 安全性设计值范围与要求范围之间的关系Fig.2 Relationship between design ranges and requirement range of safety

2 炸药冲击波感度的QMU评估

2.1 敏感性试验数据

感度试验等敏感性试验主要是临界刺激量xc的统计问题。临界刺激量xc是一个产品或一个样品固有的特性，当外界刺激量x≥xc时样品发火，称为响应；外界刺激量x＜xc时，样品表现为不响应。每一个样品都具有各自特有的临界刺激量，所有样品的临界刺激量服从某种概率分布。对于炸药和火工品，或者对于不同的感度试验，服从的感度分布不同，可能是正态分布、对数正态分布、逻辑施特分布，需要根据具体试验进行分析。冲击波感度和机械撞击感度分别为正态分布和对数正态分布。感度试验就是通过对临界刺激量的试验研究，利用统计方法估计感度分布参数。

敏感性数据的获取和分析，是炸药和火工品等爆炸产品安全性、可靠性评定的基础。通常的抽样问题，均为直接测试样品的特性参数，如长度、质量、密度、最大射程，并得到其分布特性。但是，对于每一个炸药样品，其临界刺激量xc是随机的，无法直接进行测试，只能对其施加外界刺激x。当x＞xc时，样品出现响应；x＜xc时，样品不出现响应；x＝xc时，样品可能响应，也可能不响应，但x＝xc的概率非常小，为小概率事件。当出现此种情况时，可认为样品发火，这在感度试验模拟时非常有用。通过各个样品的试验结果，只能知晓其临界刺激量是否大于或小于试验刺激量。对各样品施加的试验刺激量及响应情况，构成了特有的试验数据——敏感性试验数据。

2.2 安全性QMU评估方法

炸药安全性QMU评估的主要目的是根据QMU评估的关键要素，量化与炸药安全相关的不确定性和安全性能裕量。炸药安全性QMU评估需按计量方法进行试验程序设计，使用通过冲击波感度等安全性试验获得的参数，计算炸药的爆炸临界阈值和方差，估计给定置信度下低概率响应点的置信区间，用以研究炸药安全性裕量和不确定度评估方法。本研究使用 Bruceton 升降法［13－14］，按 照GJB772A－1997炸药试验方法605.1冲击波感度卡片式隔板法进行隔板试验。根据QMU评估通用框架和关键要素，对服从正态分布或对数正态分布的冲击波感度试验数据进行炸药安全性QMU评估。

为计算炸药冲击波安全性客观要求的阈值（最低性能值）Xth，首先需计算隔板试验过程参数n、A、B、M、ρ、b，按下列公式计算均值μ和方差σ［15－16］。

式中：n为一组试验中爆炸或不爆炸的总发数；ni为一组试验中，刺激量xi时爆炸或不爆炸的发数。若各刺激量处爆炸的总发数大于不爆炸的总发数，计算中取不爆炸的发数；若各刺激量处爆炸的总发数不大于不爆炸的总发数，计算中取爆炸的发数。

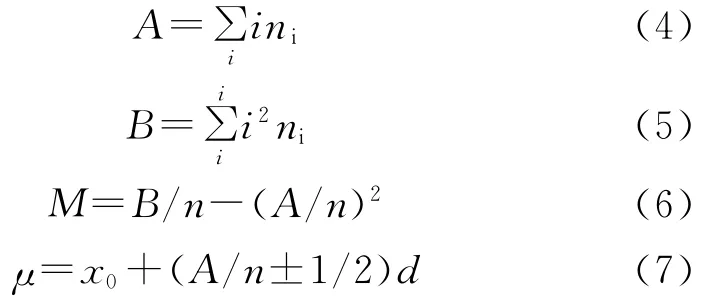
式中：d为试验步长；i为试验刺激量的台阶数。在公式（7）中，当ni为一组试验中各刺激量处爆炸总发数时，取“―”；当ni为一组试验中各刺激量处不爆炸总发数时，取“＋”。

当M≥0.3时按下式计算ρ值：

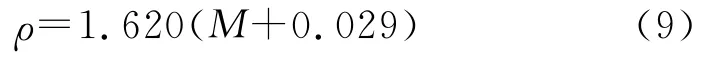
当M＜0.3时，从 GJB／Z377A－1994感度试验数理统计方法中的ρ（M、b）表得到ρ值，其中b取‖A／n－0.5‖的小数部分。对给定概率P，根据正态分布假设计算爆炸概率响应点XP为：

式中：Up为标准正态分布的P分位数。

编制隔板试验Monte－Carlo模拟程序，并采用长周期的正态随机数进行大样本量Monte－Carlo模拟，可得到方差σ估计的分布F（σ）和均值μ估计的分布F（μ），导出依赖于n、b、ρ的G、H 及σμ和σσ值。G、H 值也可从文献［15］和GJB6478－2008相关附表得到。均值μ估计、方差σ估计的标准误差分别为：

由以上各式可得：

置信水平1－α时，由以上各式可以计算XP的不确定度。根据最大似然估计的渐进正态性质，可给出XP的区间估计。对置信水平1－α，其双侧置信下限和置信上限分别为：

对隔板试验，隔板厚度越大，透过隔板入射到炸药试样中的冲击波压力越小，炸药爆炸概率越低，单侧置信上限为：

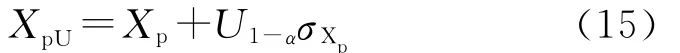
单侧置信下限为：

3 PBX－C冲击波安全性QMU评估

3.1 针对10－6爆炸概率点的QMU评估

按GJB772A－1997方法605.1冲击波感度卡片式隔板法进行PBX－C炸药隔板试验。主发药为两个Ф20mm×20mm的PBX－1药柱，相对理论密度98.5%；被发药为两个Ф20mm×20mm的PBX－C药柱，密度1.848g／cm3。试验温度22～27℃，相对湿度70%～75%，试验结果见表1。

表1 PBX－C药柱的隔板试验结果Table 1 Gap test results of PBX－C explosive cylinder

从表1可知，步长x0＝23.0mm，d＝0.5mm，试验总发数N＝26，其中爆炸总发数与不爆炸总发数均为13。以爆炸总发数n＝13按公式（3）～（9）进行计算，可得A＝11、B＝13、M＝0.28、b＝0.35、ρ＝0.52，均值μ＝23.2mm、方差σ＝0.26。进一步计算或查表可得G＝1.134，H＝1.146。

将标准正态分布10－6分位数U＝4.753 4，代入相关公式得：

置信水平0.999 9时，U＝3.719，其单侧置信上限为：

从隔板试验得到PBX－C炸药的爆炸概率为10－6要求的阈值Xth为24.4mm。置信水平为0.999 9时，Xth与X10－6上限间的不确定区间宽度U为1.5mm，冲击波安全性设计值X0为26.0mm，有M＝X0－Xth＝1.6mm，Q＝M／U＞1。在置信水平0.9999时，PBX－C炸药的冲击波感度可满足爆炸概率不高于10－6的安全性要求。

3.2 针对10－4爆炸概率点的QMU评估

将标准正态分布10－4分位数U＝3.719，代入相关公式得：

对置信水平0.999 9，其单侧置信上限为：

从隔板试验得到PBX－C炸药的爆炸概率为10－4要求的阈值Xth为24.2mm。置信水平0.999 9时，Xth与X10－4上限间的不确定区间宽度U 为1.2mm。若炸药冲击波安全性设计值X0为25.5mm，有M＝X0－Xth＝1.3mm，Q＝M／U＞1。在置信水平0.999 9时，PBX－C炸药的冲击波感度可满足爆炸概率不高于10－4的安全性要求。

3.3 评估结果分析

通过对大样本量升降法试验的Monte－Carlo模拟，对试验参数进行统计与分析，可以得到系列统计公式（3）～（16），能够进一步针对预定爆炸概率响应点进行炸药冲击波作用下安全性QMU评估。对炸药和火工品，感度试验的刺激强度随落高、电压、电流、撞击速度、作用时间等刺激量的增加，安全性变差。对该类感度试验，应使用公式（16）计算给定置信水平时单侧置信下限，进一步进行相关安全性的QMU评估。

本研究使用隔板试验进行冲击波作用下炸药安全性QMU评估。隔板厚度越大，入射到被测炸药试样的冲击波压力越低［17］。因此，在公式（10）中取加号，用公式（15）计算给定置信度时单侧置信上限。

确定安全性设计值也是一个复杂的问题，理想情况应当由理论计算得出。目前，在缺乏相关精密计算模型的情况下，只能从炸药和火工品设计的边界条件得到，存在一定局限性，冲击波作用下炸药安全性的QMU评估有待进一步深入开展。

4 结 论

（1）采用序贯升降法试验和大样本量 Monte－Carlo模拟方法研究炸药50%爆炸响应的刺激量和相关统计参量，得到给定爆炸概率响应点要求的阈值Xth、Xp点估计值的标准偏差和给定置信水平时的单侧置信上、下限估计值，进而在给定安全设计值时，进行炸药单物理参量安全性QMU评估。

（2）由于试验样品的随机性，试验获得均值、方差等参数对评估结果有一定影响，研究估计精度更高的新序贯试验方法，可以得到更为精确的均值、方差等参数，进行安全性QMU评估的效果会更好。

（3）对复杂武器系统中炸药和火工品安全性的QMU评估涉及二维及以上物理参量，需使用多维联合分布函数进行安全性QMU评估。

［1］ Sigma X，Adams M，Cornwall J，et al.Evaluation of Quantification of Margins and Uncertainties Methodology for Assessing and Certifying the Reliability of the Nuclear Stockpile［M］.Washington D C：The National Academies Press，2008，5.

［2］ Roache P J.Verification and Validation in Computational Science and Engineering［M］.Albuquerque N M：Hermosa Publishers，1998.

［3］ Trucano T G，Swiler L P，Igusa T，et al.Calibration，validation，and sensitivity analysis：what’s what［J］.Reliability Engineering and System Safety，91（10／11），2006：1331－1357.

［4］ Sharp D H，Wood－Schultz M M.QMU and nuclear weapons certification：what′s under the hood［J］.Los Alamos Science 28，2003：48.

［5］ Saltelli A，Chan K P S，Scott E M，et al.Sensitivity A－nalysis［M］.New York：John Wiley and Sons，2008.

［6］ Frey H C，Patil S R.Identification and Review of Sensitivity Analysis Methods［J］.Risk Analysis，2002，22（3）：553－578.

［7］ GJB772A－1997，炸药试验方法［S］.北京：国防工业出版社，1997.

［8］ 花成，黄明.RDX／HMX炸药晶体内部缺陷表征与冲击波感度研究［J］.含能材料，2010，18（2），152－157.HUA Cheng，HUANG Ming.Intragranular defects and shock sensitivity of RDX／HMX［J］.Chinese Journal of Energetic Materials，2010，18（2）：152－157.

［9］ Paté－Cornell M E.Uncertainties in risk analysis：six levels of treatment［J］.Reliability Engineering and System Safety，54（2／3），1996：95－111.

［10］Helton J C.Uncertainty and sensitivity analysis in the presence of stochastic and subjective uncertainty［J］.Journal of Statistical Computation and Simulation，57（1／4），1997：3－76.

［11］Sharp D H，Wood－Schultz M M.QMU and nuclear weapons certification－what′s under the hood［J］.Los Alamos Science 28，2003：47－53.

［12］Pilch M，Trucano T G，Helton J C.“Ideas Underlying Quantification of Margins and Uncertainties（QMU）：A white paper”，SAND2006－5001［R］.［S.L.］：Sandia National Laboratories report，2006.

［13］GJB／2377A－94，感度试验用数据统计方法［S］.北京：国防科工委军标出版发行部出版，1995.

［14］LIU Cun－li，WANG Shu－ping，WU Zhan－Cheng，et al.Study on the test method of the electrostatic sensitivity of the non－initiating explosive devices［J］.Journal of Electrostatics，2011，69：501－503.

［15］GJB6478－2008，火工品可靠性计数—计量综合评估方法［S］.北京：国防工业出版社，2008.

［16］刘宝光.敏感性数据分析与可靠性评定［M］.北京：国防工业出版社，1995.

［17］花成，傅华，田勇.冲击波作用下HMX晶体的细观响应［J］.火炸药学报，2010，33（3）：5－8.HUA Cheng，FU Hua，TIAN Yong.Meso－scale response of HMX crystal under the shock wave effect［J］.Chinese Journal of Explosives and Propellants，2010，33（3）：5－8.