轮-带驱动系统稳态周期响应谐波平衡分析*
2015-09-17李大鹏储德林丁虎
李大鹏 储德林 丁虎†
(1.上海大学上海市应用数学和力学研究所,上海 200072)(2.陆军军官学院应用物理研究所,合肥 230031)
轮-带驱动系统稳态周期响应谐波平衡分析*
李大鹏1储德林2丁虎1†
(1.上海大学上海市应用数学和力学研究所,上海 200072)(2.陆军军官学院应用物理研究所,合肥 230031)
研究含有单向离合器、两滑轮及附件的轮-带驱动系统稳定稳态周期响应.通过单向离合器连接从动轮与附属系统,并计入传送带的横向振动的影响,导出了由偏微分-积分方程与分段常微分方程组成的连续-离散型非线性耦合方程组.利用Galerkin方法将连续非线性方程组截断为一组非线性常微分方程组,再运用谐波平衡法得到轮-带驱动系统耦合非线性振动的稳态响应.通过比较有无单向离合器装置的系统稳定稳态幅频响应曲线,研究了单向离合器对驱动系统以及轮-带系统非线性动态特性的影响.并首次研究了高频激励下轮-带系统的稳态响应.最后,运用Runge-Kutta方法对比验证了基于谐波平衡法得到的稳态响应.
非线性, 单向离合器, 轮带系统, 谐波平衡法, 稳态响应
引言
单向离合器已经广泛应用于众多的动力系统,其主要功能是将因轮-带系统振动而引起的在非驱动方向上动力的传递解耦.轮-带传动系统在许多机械系统中起着非常重要的作用.因而这样的系统一直广受研究者关注[1-3].为了确保含单向离合器的皮带传动系统能够稳定工作,研究系统的振动特性是很有必要的.
Zhu 和 Parker[4-5]建立双自由度模型研究了带有单向离合器的两轮皮带系统的非线性动力学模型.单向离合器简化为一个不连续刚度的非线性弹簧模型,且离合器扭矩仅在驱动轮与附件轴正向相对运动时传递.他们发现单向离合器的非线性弹簧类似减震器可以减轻振动.Mocknsturm和Balaji[6]研究了咬合状态时一个自由度、分离状态时两个自由度的含单向离合器动力系统.Cheon[7]使用了离散系统研究分析了带有一单向离合器齿轮副的非线性行为.上官文斌等[8]建立了含有单向离合器装置的三轮-多楔带系统非线性振动模型,并进行了参数优化设计,使系统中张紧臂角度、单向离合器扭矩等波动的幅值得到了降低.
以上的这些研究工作都忽略了驱动带的横向振动,将带模型化为无质量的弹簧.Ding 和 Zu[9-10]建立了一个描述驱动轮、从动轮和附件轴旋转的模型,同时考虑了传送带的横向振动,通过Galerkin截断[11-12]结合 Runge-Kutta 方法,研究了低频激励下,单向离合器对系统耦合振动的影响.
本文采用基于傅里叶变换的谐波平衡法[13]求解轮-带驱动系统耦合非线性振动的稳态响应.通过比较系统有无单向离合器装置的稳态幅频响应曲线,研究了单向离合器对动力系统的影响.并考察高频激励下轮-带驱动系统的稳态幅频响应.最后,运用Runge-Kutta算法对比验证基于谐波平衡法得到的稳态响应结果.
1 振动控制方程
本文采用两个滑轮和一个单向离合器的皮带驱动系统模型[14],如图1所示.从动滑轮和附件轴由刚度为Ka的环绕弹簧连接.当从动滑轮与附件轴分离时,弹簧被断开,与轴刚性的连接在一起的附属部分起负载作用.假设传送带属性(带密度ρ,带模量EA,其中E是杨氏模量;A是横截面的面积)是均匀的.皮带的轴向平移速度c也被假设是恒定和均匀的.θi(t)、Ji、ri以及 Mi分别是角位移、转动惯量、半径以及从动滑轮和驱动滑轮的预力矩.Ja和θa(t)分别是附属部分转动惯量和角位移.当从动滑轮的角位移小于附属的角位移时,单向离合器分离.li(i=1,2)为带段i的长度.中性轴的坐标x和时间t,wi(x,t)和ui(i=1,2)分别为带跨度i的横向位移和纵向位移.假设驱动滑轮与从动滑轮具有相同大小,即l1=l2=l,J1=J2=J,r1=r2=r'.此外,在传动系统的建模中作如下假设:(Ⅰ)皮带的弯曲刚度很小可以忽略不计,因此皮带可以简化为一个弹簧模型;(Ⅱ)忽略滑轮上的皮带打滑情况.

图1 含两滑轮和单向离合器的带传动系统Fig.1 Belt-drive system with two pulleys and a one-way clutch
传送带的运动方程为
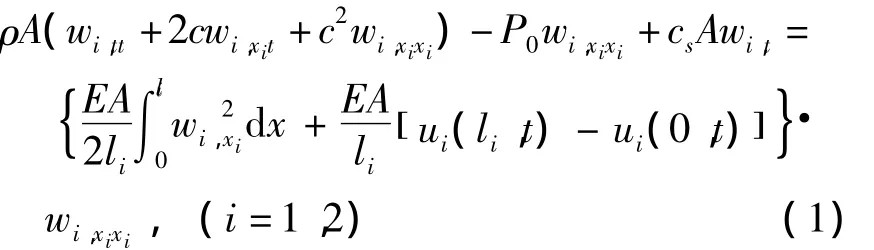
其中下标x和t是分别指对x和t的偏微分,P0为传送带的轴向初始静态张力.传送带的边界条件为
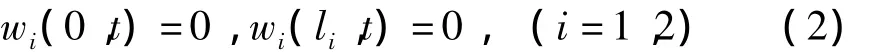
主动带轮的运动方程为

从动滑轮和附件轴的运动方程为

其中ca为离合器阻尼系数,δθ=θp-θa,Tt(δθ)为离合器扭矩.单向离合器的咬合与分离基于从动滑轮与附件轴间的相对角位移.当从动滑轮的旋转角位移θp大于附件轴的旋转角位移θa时,离合器咬合.相应的,当从动滑轮旋转的角位移小于附件轴旋转的角位移时附件轴的运动从动滑轮中解耦出来,此时,从动滑轮与附件轴之间的没有了机械连接,即仅当从动滑轮与附件轴咬合时,从动滑轮才向附件轴传递力矩.通过离合器传递的扭矩可用分段函数表示

在本文中,通过下列无量纲变量和参数将方程(1)、(3)、(4)表示为无量纲化形式

其中无量纲参数c为轴向速度.无量纲参数cs、cb和ca分别为皮带横向运动的阻尼系数、皮带与滑轮间的摩擦阻尼系数和附件的阻尼系数.无量纲参数k1被称为非线性系数,表征传动带的非线性影响.轴向传动带的横向运动和驱动皮带滑轮、从动滑轮与附件轴的无量纲方程可由方程(6)定义的新参数表示.带的无量纲边界条件与有量纲条件相同,由方程(2)描述.驱动滑轮是基于引擎特性设定的,驱动滑轮以θ2=Amcosωt的角速度运动.无量纲参数Am(本文取Am=0.01)表示驱动轮带运动的振幅.保留方程(7)和(8)中所有包含θ2的项作为激励项.激励频率ω为驱动滑轮转动速度的s倍,其中s表示2s汽缸发动机(本文采用s=3).带的转动与引擎速度关系式为c=r1ω/sl.引用无量纲参数代替激励频率ω.

2 Galerkin截断
在本研究中,为了减少谐波平衡法中因为傅里叶变换与逆变换次数的增加带来的误差的影响,在不影响结果准确性的前提下减小方程运算复杂程度,故只需采用2阶Galerkin截断.此外,选用边界条件下静态张力弹性弹簧的本征函数为试函数,假设方程(7)的解采用如下形式

其中 qi(t)(i=1,2)和 qi(t)(i=3,4)分别为带 1和带2一系列广义位移.将方程(9)代入方程(7)得到下列一系列二阶常微分方程

将方程(10)的第一个等式乘以sin(kπx1)(k=1,2),第二个等式乘以 sin(kπx2)(k=1,2)并在区间[0,1]积分,得


3 谐波平衡法
考虑到该系统响应具有周期性,故可以将所有解展开为R次谐波傅里叶级数[11]:

由于方程的相似性可将式(12)分解后统一写为:

由周期性可知 qx(θ)=qx(θ+T),θp=θp(θ+T),故 f(qx,θp)=f(θ+T),周期函数 f(qx,θp)进行Fourier级数展开
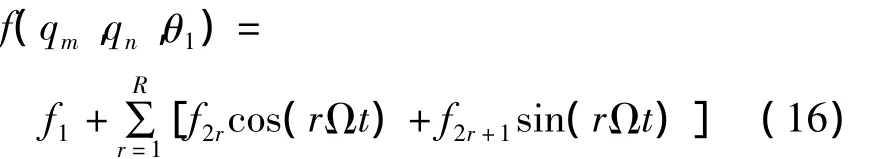
将展开为Fourier级数的各项(14)、(16)代入(15)中,令方程两边的常数项、各次正弦谐波、余弦谐波的系数相等,得到由(2R+1)N个方程构成的代数方程组si=0.


对于方程(13),为了方便对系统动态响应进行迭代求解,将单向离合器弹簧扭矩中分段函数部分用双曲正切函数表达成连续函数形式
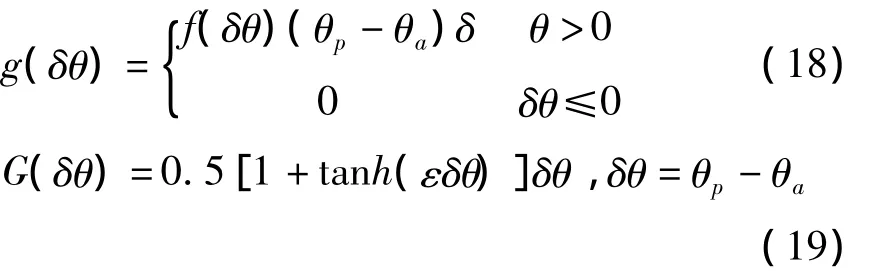
其中ε取10000[4].由于响应的周期性,方程(13)同样可以通过傅里叶变换谐波平衡方法得出相对应的平衡方程,此时qx用傅里叶展开形式代入,分别令这两个方程两边的常数项、各次正弦谐波、余弦谐波的系数相等得到如下方程组:


其中当r不等于1时,-2k1r'A/l项为0,系数h(m)在m=1,2,3,4 时分别等于1,4,-1,-4.在非线性代数方程组(17)、(20)和(21)中,稳态响应qx、θp、θa的 Fourier级数各项系数ur是待求的未知量,由于f(qx,θp)、G(δθ)是关于qx、θp、θa的函数,函数f(qx,θp)、G(δθ)对应的的 Fourier级数各次谐波系数fr、Fr也是未知量ur的函数,因此,求解之前必须把fr、Fr表示成ur的表达式.由于fr、Fr和ur是各自函数的Fourier级数系数,采用Fourier变换和逆变换实现两者之间的联系,步骤如下:
(1)离散傅里叶逆变换(IDFT):给定变量qx、θp、θa的 Fourier系数ur,通过离散傅里叶变换的逆变换得到qx、θp、θa在一个时域周期之内的离散时间序列qn、θpn、θan

由qx、θp、θa的时间序列qn、θpn、θan确定fn(qx,θp)的时间序列gn

(2)离散傅里叶变换(DFT):对gn、Gn进行傅里叶变换可得到频域内f、F的傅里叶系数fr、Fr

最终代入式(17)、(20)和(21)中,得到只关于未知变量u的非线性代数方程组.本文采用基于拟牛顿法的Broyden方法求解非线性代数方程组.给出u的一组初值,用迭代方法求解即可得到系统的稳态响应.
4 稳态响应
表1列出了皮带传动系统的物理和几何特性[5-6]和方程(11)中的无量纲参数计算值.

表1 含单向离合器的传送带属性Table 1 Properties of the belt- drive with one-way clutch
4.1 谐波平衡法
图2(a)和2(b)分别表示从动滑轮和附件轴有无离合器时的稳态响应.从图中可以看到跳跃现象及典型的非线性现象;从动滑轮与附件轴的共振区域宽于带段;单向离合器减小了从动滑轮和附件轴的共振.同时带的非线性张力运动作用使从动滑轮和附件轴在不含离合器时均产生了跳跃现象.而在含单向离合器时,在从动滑轮和附件轴图形中均可看到振峰的软化.由此可知,软化非线性是单向离合器作用产生的结果.也就是说,单向离合器使稳态幅频响应曲线向左侧弯曲.由图2(c)和2(d)可知,平移带共振区域的减少是由于皮带传动系统含有离合器的作用.此外,不含离合器的带段的稳态响应表明共振高峰的软化和硬化非线性均在同一时间.而含有单向离合器时,平移带的共振高峰的软化非线性消失.
图3给出了系统在频率范围为[1000,2000]的共振稳态幅频特性曲线,其中Am=0.014,Ka=1300.从图中仍可以看到跳跃现象及典型的非线性现象;从动滑轮的共振区域宽于带段.图3(a)表明,单向离合装置能够有效的降低共振时的响应振幅.但是,图3(b)显示,虽然单向离合装置减小了带的共振响应振幅,却使得带的共振区域增大了.同时联系图3(a)与图3(b)发现,轮-带系统绞合时带段1在频率[1100,1200]区间没有共振而含单向离合器时却发生了振幅较小的共振,这是由于单向离合器对轮-带系统作用时导致系统固有频率发生改变而引起的.

图2 比较有无单向离合器的系统稳态响应曲线Fig.2 The comparisons of the steady-state response with and without clutch

图3 比较有无单向离合器的系统稳态响应曲线Fig.3 The comparisons of the steady-state response with and without one-way clutch
4.2 数值验证
当该轮带动力系统中所有参数均与文献[10]相同时,通过对比谐波平衡法与4阶Runge-Kutta方法在系统有无离合器作用下所得到的稳态响应曲线如图4所示,从图中对比附件轴和带段1在有无单向离合器作用下的图形,可知谐波平衡法与Runge-Kutta方法所得到的结果是非常的接近的.

图4 谐波平衡法与Runge-Kutta方法的比较Fig.4 The comparisons of the harmonic balance method and the Runge-Kutta algorithm
5 结论
研究了一个非线性离散-连续耦合轮-带驱动系统,该系统中驱动轮、从动轮和附件轴的旋转运动与传动带的横向振动相耦合.利用Galerkin截断法将非线性连续方程组离散化为一组二阶非线性常微分方程,并运用谐波平衡法进行求解系统的稳定稳态响应.通过与4阶Runge-Kutta方法对比,验证了本文的谐波平衡法具有精度.研究发现,对于低频共振,单向离合器不仅降低了从动滑轮和附件轴旋转振动共振的振幅,而且还减小了带横向振动的共振区域.同时观察到带的非线性张力运动作用使从动滑轮和附件轴在不含离合器时也会产生软特性的跳跃现象.另外,高频激励的共振响应分析表明,单向离合装置在减小了带的共振响应振幅的同时,增大了带的共振区域.
1 陈立群.平带驱动系统的振动分析研究进展.力学与实践,2001,23(4):8~12(Chen L Q.Advance in analysis of vibration of serpentine belt drive systems.Mechanics in Engineering,2001,23(4):8 ~12(in Chinese))
2 Cassidy R L,Fan S K,Macdonald R S,et al.Serpentineextended life accessory drive.SAE International,1979:790699
3 Abrate S.Vibrations of belts and belt drives.Mechanism and Machine Theory,1992,27(3):645 ~659
4 Zhu F,Parker R G.Non-linear dynamics of a one-way clutch in belt-pulley systems.Journal of Sound and Vibration,2005,279(1-2):285~308
5 Zhu F,Parker R G.Perturbation analysis of a clearancetype nonlinear system.Journal of Sound and Vibration,2006,292(3-5):969~979
6 Mockensturm E M,Balaji R.Piece-wise linear dynamic systems with one-way clutches.ASME Journal of Vibration and Acoustics,2005,127(5):475 ~482
7 Cheon G J.Nonlinear behavior analysis of spur gear pairs with a one-way clutch.Journal of Sound and Vibration,2007,304(3-5):18~30
8 张少飞,上官文斌.具有单向离合器的多楔带附件驱动系统旋转振动建模及参数优化设计.振动与冲击,2012,31(13):163~168(Zhang S F,ShangGuan W B.Rotational vibration modeling and optimization design of serpen-tine belt accessory drive system with one-way clutch.Journal of Vibration and Shock,2002,31(13):58 ~ 61(in Chinese))
9 Ding H,Zu J W.Periodic and chaotic responses of an axially accelerating viscolastic beam under two-frequency excitations.International Journal of Applied Mechanics,2013,5(2):1350019
10 Ding H,Zu J W.Effect of one-way clutch on the nonlinear vibration of belt-drive systems with a continuous belt model.Journal of Sound and Vibration,2013,332(24):6472~6487
11 赵跃宇,李永鼎,王连华,康厚军.悬索的超谐波共振与1∶3内共振分析.动力学与控制学报,2007,5(2):112~117(Zhao Y Y,Li Y D,Wang L H,Kang H J.On the one-to-three internal resonances and superharmonic resonances of suspended cables.Journal of Dynamics and Control,2007,5(2):112 ~117(in Chinese))
12 宋敉淘,曹登庆.应用非线性Galerkin方法求解微梁的动态响应.动力学与控制学报.2009,7(3):205~211(Song M T,Cao D Q.Dynamical responses of microbeams using nonlinear Galerkin method.Journal of Dynamics and Control,2009,7(3):205 ~ 211(in Chinese))
13 孙涛,胡海岩.基于傅里叶变换与谐波平衡法的行星齿轮系统非线性动力学分析.机械工程学,2002,38(11):58~61(Sun T,Hu H Y.Nonlinear dynamics of planetary gear transmission by harmonic balance method based on DFT.Journal of Mechanical Engineering,2002,38(11):58~61(in Chinese))
14 丁虎,陈立群,张国策.轴向运动梁横向非线性振动模型研究进展.动力学与控制学报,2013,11(1):20-30(Advanced in nonlinear models for transverse vibration of axially moving beams.Journal of Dynamics and Control,2013,11(1):20 ~30(in Chinese))
*The project supported by the State Key Program of National Natural Science Foundation of China(11232009),and the National Natural Science Foundation of China(11372171,11422214)
† Corresponding author E-mail:dinghu3@shu.edu.cn
THE FREQUENCY-RESPONSE CURVE OF A BELT-DRIVE SYSTEM BY USING THE HARMONIC BALANCE METHOD*
Li Dapeng1Chu Delin2Ding Hu1†
(1.Shanghai Institute of Applied Mathematics and Mechanics,Shanghai200072,China)(2.Institute of Applied Physics,Army officer Academy,Hefei230031,China)
This paper studied a belt-drive system containing a translating belt,two pulleys,accessory systems,and a one-way clutch.The driven pulley and the accessory system were coupled by the one-way clutch.Moreover,the transverse vibration of the translating belt was taken into account.Therefore,the derived coupled discrete-continuous nonlinear equations consist of integro-partial-differential equations and piece-wise ordinary differential equations.The continuous nonlinear equations were truncated to a set of nonlinear ordinary differential equations by using the Galerkin method.The steady-state responses of the coupled vibration of the belt-drive system were investigated by the numerical harmonic balance method.Moreover,the effects of the one-way clutch on the power system were studied by comparing the frequency-response curve of the translating belt with and without one-way clutch device.The nonlinear dynamic characteristics of the belt-drive system were studied.Furthermore,the steady-state responses of the belt-drive system were investigated at the higher excitation frequency for the first time.In addition,the steady-state responses based on the harmonic balance method were confirmed by the Runge-Kutta algorithm.
nonlinearity, one-way clutch, belt-drive system, harmonic balance method, steady-state response
10 July 2014,
15 September 2014.
10.6052/1672-6553-2014-079
2014-07-10 收到第 1 稿,2014-09-15 收到修改稿.
*国家自然科学基金资助项目(11232009,11372171,11422214)
E-mail:dinghu3@shu.edu.cn
