混合突触作用下耦合时滞对模块神经元网络簇同步的影响*
2015-09-17胡丽萍杨晓丽孙中奎
胡丽萍 杨晓丽† 孙中奎
(1.陕西师范大学数学与信息科学学院,西安 710062)(2.西北工业大学应用数学系,西安 710072)
混合突触作用下耦合时滞对模块神经元网络簇同步的影响*
胡丽萍1杨晓丽1†孙中奎2
(1.陕西师范大学数学与信息科学学院,西安 710062)(2.西北工业大学应用数学系,西安 710072)
针对电突触耦合和化学突触耦合混合作用下含有耦合时滞的模块神经元网络,利用非线性动力学理论和数值仿真方法,探讨了耦合强度及耦合时滞对模块神经元网络簇同步特性的影响.结果发现,模块神经元网络中子网络内、子网络间的耦合强度都能促使簇放电神经元取得簇同步,但是时滞却对耦合诱导的簇同步具有显著的抑制作用.进一步的研究证实了本文所得的研究结果不依赖于子网络的数目与子网络的节点个数.需要指出的是,耦合时滞对神经元网络簇同步的抑制作用对治疗簇同步引发的一些神经性疾病(如帕金森病、癫痫等)具有一定的理论指导意义.
模块神经元网络, 簇同步, 混合突触, 耦合时滞
引言
同步是神经元系统一种重要的非线性现象.随着复杂网络的兴起,神经元网络上的同步动力学在不同领域中得到了大量研究[1-3].特别对于神经元网络上的簇同步,近年来也吸引了不少研究者的关注[4-5].文献[6-8]分别探讨了全局耦合网络、小世界网络、无标度网络中耦合强度对簇放电神经元簇同步的影响,揭示了当耦合强度足够大时,神经元能够取得簇同步.
神经元之间有两种基本的耦合方式,即电突触耦合和化学突触耦合.前者通过缝隙连接实现,而后者通过树突和轴突实现连接.在以往的研究中,绝大部分文献探讨了电突触耦合或化学突触耦合对耦合神经元动力学特性的影响.值得注意的是,近期的研究表明,两种突触耦合方式在耦合神经元间是可以同时存在的[9-14],并且突触耦合对神经元网络的同步动力学行为具有关键性影响.例如Kopell等发现电突触耦合和化学突触耦合对神经元网络的完全同步的影响不同,但却具有相互补充的作用[9].Baptista 等进一步在 Hindmarch-Rose 神经元构成的小世界网络中,研究了两种突触耦合方式对神经元完全同步的影响,揭示了混合突触耦合有助于同步的形成[10].同时,由于信号传输速度的有限性和递质释放的滞后,时滞在耦合神经元之间也是普遍存在的.已有的研究表明,耦合时滞对神经元网络上的同步、共振、时空有序等动力学特性也具有促进或增强、抑制或减弱等作用[15-18].
最新关于猕猴和猫大脑皮层的分析表明,脑皮层的神经元网络具有模块结构[19-20].从而关于模块神经元网络的同步动力学也吸引了一些研究者的关注.例如,Batista等针对化学突触耦合的小世界模块网络,研究了具有簇放电离散神经元的簇同步[21];于等在电突触耦合的小世界模块网络中,分析了子网络间耦合强度和子网络内耦合强度对耦合簇放电神经元簇同步的影响[22].
基于以上的分析,我们进一步思考:既然耦合神经元之间进行信息传递时电突触耦合和化学突触耦合同时存在[9-14],并且耦合时滞客观存在于神经元网络,那么对于簇放电的模块神经元网络,在电突触耦合和化学突触耦合的混合作用下,耦合神经元之间能否达到簇同步?耦合时滞对模块神经元网络的簇同步又有什么影响?本文针对该问题展开系统研究.首先,我们构建了子网络是无标度网络的模块神经元网络模型、引入了刻画神经元簇同步特性的两种方法;然后,通过数值模拟,我们研究了子网络内与子网络间耦合强度、耦合时滞对模块神经元网络簇同步的影响.
1 构建数学模型和诊断分析方法
1.1 模块神经元网络模型
模块网络是由几个子网络构成的复杂网络.子网络可以是规则网络、小世界网络或无标度网络.本文假设模块网络中含有M个子网络,每个子网络是N个节点的无标度网络.首先构建无标度网络:生成含m0个节点的全连接网络,每隔相等时间间隔增加一个新的节点,新节点与m个不同的已经存在于网络中的旧节点相连产生m条新边,新节点与旧节点i相连的概率Π取决于节点i的度数,经过n时间步后,即可生成一个无标度网络.利用类似的方法,我们可以产生M个无标度网络.其次,从第I个和第J(I,J=1,2,…,M,且J≠I)个子网络中随机选择一对节点,并以概率pinter在选取的节点对之间引入一条边.按照这种方式,我们构造了模块网络.不失一般性,下文假设网络结构的参数如下:MN=200,m0=2,m=2,pinter=0.01.
本文利用二维离散Rulkov神经元[22]来刻画模块网络中节点上的局部动力学.于是,模块神经元网络模型的动力学方程组可以描述为

这里,(I,i)表示第I个子网络的第i个神经元,i=1,2,…,N,I=1,2,…,M;x代表神经元的膜电位,y是恢复变量;σ和β为模型参数,其取值为 σ=0.001 和 β=0.001,αI,i服从区间[ 4.1,4.4 ] 上的均匀分布,此时单个神经元具有混沌簇放电行为.(n)是耦合项,具体表达式为
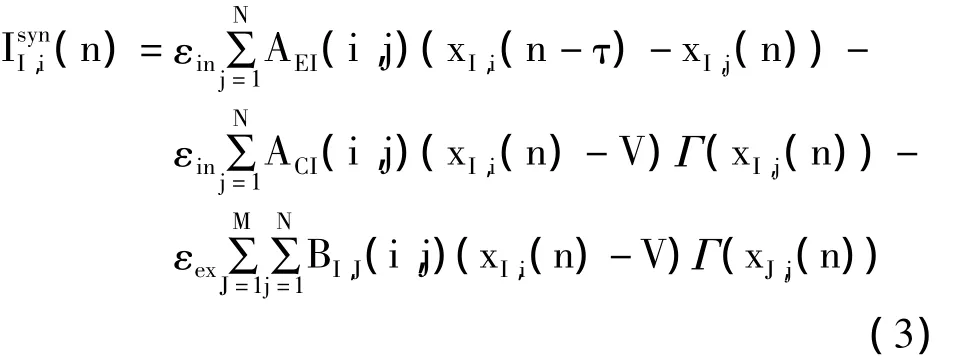
其中,εin刻画子网络内耦合神经元间的耦合强度(简称内耦合强度);εex刻画子网络间耦合神经元间的耦合强度(简称为外耦合强度);V代表突触反电势,取V=1.8,此时表示兴奋性化学突触;如果第I个子网络内的第i个神经元与第j个神经元通过化学突触作用进行耦合,则ACI(i,j)=ACI(j,i)=1;如果第I个子网络内的第i个神经元与第j个神经元通过电突触作用进行耦合,则AEI(i,j)=AEI(j,i)=1;否则,ACI(i,j)=ACI(j,i)=0 ,AEI(i,j)=AEI(j,i)=0 .如果第I个子网络的第i个神经元与第J个子网络的第j个神经元通过化学突触作用进行耦合,则BI,J(i,j)=BJ,I(j,i)=1 ,否则,BI,J(i,j)=BJ,I(j,i)=0 .S型函数为Γ(xj)=1/(1+exp {-λ[xj(k-τ)-Θs]}),其中Θs=-1.0,λ表示突触前神经元影响突触后神经元的一个阈值,这里取λ=30.τ表示神经元之间进行信息传递时的延迟时间.每个子网络内化学突触耦合转化成电突触耦合的概率为f,本文设定f=0.1 .
1.2 诊断分析方法
本文借助于数值计算序参数R[21-22]来衡量模块神经元网络的簇同步特性,其定义式为
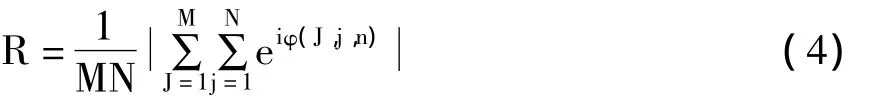
这里,φ(J,j,n)表示第J个子网络中的第j个神经元在时刻n处的簇放电相位,具体为
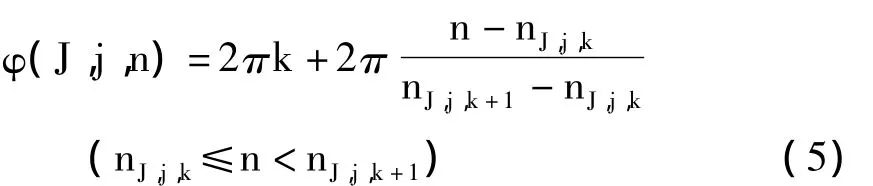
其中,nJ,j,k是第J个子网络中第j个神经元的第k个簇开始放电的时刻.一般地,R的值越大,表明神经元网络簇同步的程度越大,特别的,当所有神经元簇放电达到同步时,簇相位几乎一致,从而R接近于1;相反的,当所有簇放电神经元处于完全不同步状态时,簇相位几乎不相关,从而R≈0.
另外,本文还利用耦合神经元膜电位的平均场方差Var(X)来定量刻画耦合神经元的簇同步特性,其中X表示模块神经元网络的平均场,具体为
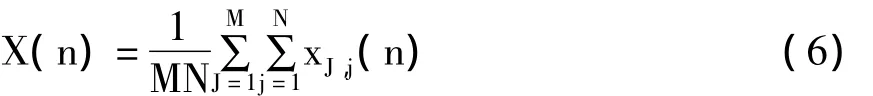
当网络中所有神经元以相同的节律放电时,平均场序列呈现出类似周期的大幅振荡,对应的Var(X)值较大;而当网络中所有神经元都自行放电时,平均场序列表现出近似随机的小幅振荡,相应的Var(X)值较小.所以,Var(X)值越大,耦合神经元之间簇同步的效果越好.
2 簇同步动力学特性分析
在这一部分,我们首先讨论当耦合项(3)不含时滞(即τ=0时),模块神经元网络在电突触耦合和化学突触耦合混合作用下的簇同步动力学.然后,我们在耦合项中引入时滞,进一步探究耦合时滞对模块神经元网络簇同步特性的影响.
2.1 耦合强度诱导的簇同步
当τ=0时,我们分别研究内耦合强度εin、外耦合强度εex对模块神经元网络簇同步特性的显著性影响.
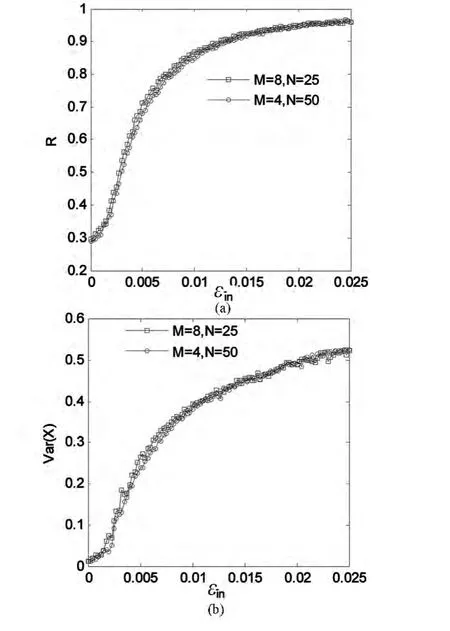
1 序参数R和平均场方差Var(X)随内耦合强度εin的变化曲线:(a)序参数;(b)平均场方差Fig.1 The order parameter R and the variance of the mean field Var(X)as variation of the intra-coupling strength εin:(a)The order parameter,(b)The variance of the mean field
首先我们通过数值计算序参数R、平均场方差Var(X)及网络的时空图来研究内耦合强度εin对模块神经元网络簇同步的影响.当εex=0.01,M=8,N=25时,图1分别刻画序参数R和平均场方差Var(X)随着内耦合强度εin的演化规律.由图1(a)可知,随着εin的增大,R不断增大,并且在εin较小时R的增长速度很快,当εin超过某一临界值(εin≈0.01)时,R增长速度减慢并逐渐趋向1,这表明模块神经元网络在内耦合强度作用下逐渐达到簇同步.图1(b)展示了平均场方差Var(X)与内耦合强度εin的依赖关系.由该图形不难观察到,Var(X)随着εin的增加而不断增加,这也表明模块网络中耦合神经元在内耦合强度作用下,放电节律逐渐趋于一致,从而模块神经元网络的簇同步效果越来越好.
图2刻画了在不同内耦合强度作用下,模块神经元网络的时空图.当εin=0时,如图2(a)所示,此时耦合神经元的簇放电节律不一致,模块神经元网络的时空图处于混乱状态.随着εin的增大,如εin=0.0025,如图2(b)所示,此时耦合神经元的簇放电节律逐渐趋于一致.进一步增大内耦合强度,如εin=0.02,如图2(c)所示,此时耦合神经元的簇放电节律基本趋于一致,模块神经元网络的时空图处于比较有序状态.不难看出,借助于模块神经元网络的时空图演化图,我们进一步揭示了内耦合强度对耦合神经元簇同步的积极作用.

图2 在不同内耦合强度下,模块神经元网络的时空图Fig.2 The space-time plots of modular neuronal network for different intra-coupling strengths
当改变模块神经元网络的子网络个数及节点数目时,如M=4,N=50,图1(a)与1(b)中也分别刻画了此情形下序参数R及平均场方差Var(X)随内耦合强度εin的演化曲线.易观察到:随着εin的增加,R与Var(X)都呈现不断增加的趋势,并且与M=8,N=25情形下的演化曲线基本一致.这一结果表明内耦合强度诱导模块神经元网络达到簇同步对子网络个数及节点数目具有一定的鲁棒性.
本文进一步利用序参数R、平均场方差Var(X)讨论了外耦合强度εex对模块神经元网络簇同步特性的影响.当 εin=0.012,M=8,N=25时,图3分别描述了序参数R、平均场方差Var(X)和外耦合强度εex的依赖关系.从图3(a)中我们不难观察到,R随εex的增加而增加,表明在外耦合强度作用下耦合神经元簇同步效果越来越明显.图3(b)刻画了平均场方差Var(X)随着外耦合强度εex的变化趋势,显然地,Var(X)也是随着εex的增大而增大,这同样说明较大的外耦合强度对模块神经网络的簇同步效果具有积极作用.当改变网络的拓扑结构时,如M=4,N=50,图3也分别刻画了此情形下序参数R及平均场方差Var(X)随外耦合强度εex的演化曲线.很明显,序参数R及平均场方差Var(X)随外耦合强度εex的变化情况与M=8,N=25的情形基本是一致的.这一现象说明了较大的外耦合强度对模块神经元网络簇同步的积极作用不依赖于子网络的个数及子网络的节点数目.
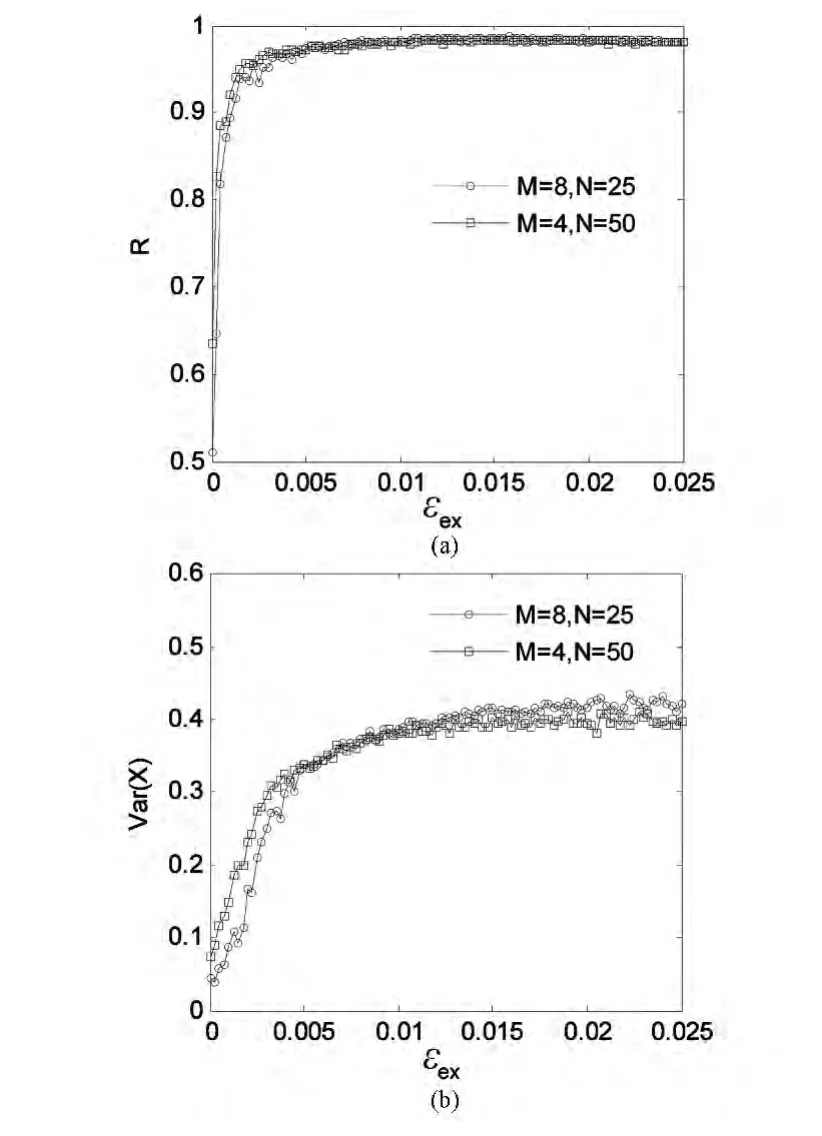
图3 序参数R和平均场方差Var(X)随外耦合强度εex的变化曲线:(a)序参数;(b)平均场方差Fig.3 The order parameter R and the variance of the mean field Var(X)as variation of the inter-coupling strength εex:(a)The order parameter,(b)The variance of the mean field
2.2 时滞对模块神经元网络簇同步的影响
在上一节的研究基础上,本小节我们将在耦合项中引入时滞,进一步研究耦合时滞对耦合强度诱导的模块神经元网络簇同步的影响.不失一般性,固定外耦合强度εex=0.01.
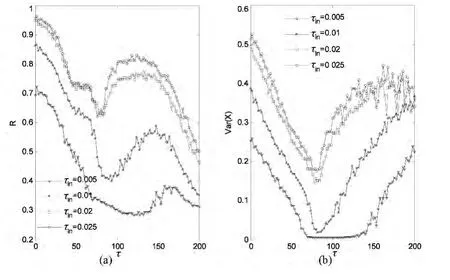
图4 序参数R和平均场方差Var(X)随时滞τ的变化曲线:(a)序参数;(b)平均场方差.网络结构参数为M=8,N=50Fig.4 The order parameter R and the variance of the mean field Var(X)as variation of the timedelay τ:(a)The order parameter,(b)The variance of the mean field.

图5 序参数R和平均场方差Var(X)随时滞τ的变化曲线:(a)序参数;(b)平均场方差.网络结构参数为M=4,N=50Fig.5 The order parameter R and the variance of the mean field Var(X)as variation of the timedelay τ:(a)The order parameter,(b)The variance of the mean field.
该部分同样利用序参数R与平均场方差Var(X)来研究耦合时滞τ对模块神经元网络簇同步的影响.图4分别展示了当M=8,N=25时,在不同的内耦合强度εin下,序参数R及平均场方差Var(X)随着时滞τ的变化曲线.从图4(a)可知,当εin=0.025时,R在τ=0处取得最大值,即R随着τ变化的值都没有超过当τ=0时R的值.图4(b)刻画了平均场方差Var(X)与时滞τ的依赖关系.显然可见,Var(X)同样在τ=0处取得最大值,即Var(X)随着τ变化的值都没有超过当τ=0时Var(X)的值.当εin取其它值时,如εin=0.005,εin=0.01,εin=0.02,R和Var(X)随τ的变化趋势相似于εin=0.025的情形.R和Var(X)随τ的演化趋势说明了耦合时滞对模块神经元网络的簇同步具有抑制作用.
当改变模块网络的拓扑结构时,如M=4,N=50,图5分别展示了不同内耦合强度下,序参数R及平均场方差Var(X)随着时滞τ的变化曲线,它们与M=8,N=25情形下的图形没有定性性质的改变,这也说明了耦合时滞对模块神经元网络的簇同步具有消极作用,并且这一消极作用不依赖于子网络的个数及子网络的节点数目.
3 结论
鉴于电突触耦合、化学突触耦合、耦合时滞在神经元进行信息传递时普遍存在,并且神经元网络具有模块特性,本文构建了混合突触作用下含有耦合时滞的模块神经元网络,借助于序参数、平均场方差及时空图,利用数值仿真讨论了耦合强度和耦合时滞对模块神经元网络簇同步特性的影响.研究结果表明,对于不同的子网络个数及子网络节点个数,子网络内和子网络间的耦合均能诱导模块神经元网络的簇同步,但是耦合时滞却对簇同步具有抑制作用.本文的研究结果丰富了神经科学的理论成果,特别地,耦合时滞对神经元网络簇同步的抑制作用对治疗簇同步引发的一些神经性疾病(如帕金森病、癫痫等)具有一定的理论指导意义.
1 Tsukamoto Y,Isomura Y,Nambu A et al.Excitatory gaba input directly drives seizure-like rhythmic synchronization in mature hippocampal CA1 pyramidal cells.Neuroscience,2003,119(1):265 ~275
2 Osipov G V,Kurths J,Zhou C.Synchronization in oscillatory networks.Berlin:Springer,2007
3 Arenas A,Diaz-Guilera A,Perez-Vicente C J.Synchronization processes in complex networks.Physica D,2006,224(1-2):27 ~34
4 Belykh I,Lange E,Hasler M.Synchronization of bursting neurons:what matters in the network topology.Physical Review Letters,2005,94(18):188101
5 Shen Y,Hou Z,Xin H.Transition to burst synchronization in coupled neuron networks.Physical Review E,2008,77(3):031920
6 Ivanchenko M V,Osipov G V,Shalfeev V D et al.Phase synchronization in ensembles of bursting oscillators.Physical Review Letters,2004,93(13):134101
7 Yu H T,Wang J,Deng B et al.Chaotic phase synchronization in small-world networks of bursting neurons.Chaos,2011,21(1):013127
8 Batista C A S,Batista A M,Pontes J A C de et al.Chaotic phase synchronization in scale-free networks of bursting neurons.Physical Review E,2007,76(1):016218
9 Kopell N,Ermentrout B.Chemical and electrical synapses perform complementary roles in the synchronization of interneuronal networks.In:Proceedings of the National Academy of Sciences,2007,101(42):15482 ~15487
10 Baptista M,Kakmeni F,Grebogi C.Combined effect of chemical and electrical synapses in Hindmarsh-Rose neural networks on synchronization and the rate of information.Physical Review E,2010,82(3):036203
11 Gibson J R,Beierlein M,Connors B W.Two networks of electrically coupled inhibitory neurons in neocortex.Nature,1999,402(6757):75 ~ 79
12 Hestrin S,Galarreta M.Electrical synapses define networks of neocortical GABAergic neurons.Trends in Neurosciences,2005,28(6):304 ~309
13 Galarreta M,Hestrin S.Electrical synapses between Gaba-Releasing interneurons.Nature Reviews Neuroscience,2001,2(6):425 ~433
14 Connors B W,Long M A.Electrical synapses in the mammalian brain.Annual Review of Neuroscience,2004,27(1):393~418
15 Wang Q Y,Perc M,Duan Z et al.Synchronization transitions on scale-free neuronal networks due to finite information transmission delays.Physical Review E,2009,80(2):026206
16 Liu C,Wang J,Wang L et al.Multiple synchronization transitions in scale-free neuronal networks with electrical and chemical hybrid synapses.Chaos,Solitons&Fractal,2014,59(1):1 ~12
17 Wang Q Y,Perc M,Duan Z et al.Delay-induced multiple stochastic resonances on scale-free neuronal networks.Chaos,2009,19(2):023112
18 Wu H,Hou Z,Xin H.Delay-enhanced spatiotemporal order in coupled neuronal systems.Chaos,2010,20(4):043140
19 Huang L,Lai Y,Gatenby R.Alternating synchronizabili-ty of complex clustered networks with regular local structure.Physical Review E,2008,77(1):016103
20 Zamora-Lopez G,Zhou C S,Kurths J.Graph analysis of cortical networks reveals complex anatomical communication substrate.Chaos,2009,19(1):015117
21 Batista C A S,Lameu E L,Batista A M et al.Phase synchronization of bursting neurons in clustered small-world networks.Physical Review E,2012,86(1):016211
22 Yu H T,Wang J,Deng B et al.Bursting synchronization in clustered neuronal networks.Chinese Physics B,2013,22(1):018701
23 Rulkov N.Regularization of synchronized chaotic bursts.Physical Review Letters,2001,86(1):183~186
*The project supported by the National Natural Science Foundation of China(11272258,11572180),the Fundamental Funds Research for the Central Universities(GK201302001)and the NSF of Shaanxi Province(2014JQ1013)
† Corresponding author E-mail:yangxiaoli@snnu.edu.cn
EFFECT OF COUPLED TIME-DELAY ON BURSTING SYNCHRONIZATION IN MODULAR NEURONAL NETWORK WITH HYBRID SYNAPSES*
Hu Liping1Yang Xiaoli1†Sun Zhongkui2
(1.College of Mathematics and Information Science,Shaanxi Normal University,Xi'an710062,China)(2.Department of Applied Mathematics,Northwestern Polytechnical University,Xi'an710072,China)
We explore the nontrivial effects of coupling strength and time-delayed coupling on bursting synchronization of modular neuronal network with hybrid chemical and electrical synapses by nonlinear dynamics and numerical simulation.The results show that the intra and inter-coupling between different neurons can induce bursting neurons to achieve bursting synchronization in modular neuronal network.However,time delays in the coupling have negative influences on the coupling-induced bursting synchronization.Furthermore,these two results are verified to be robust against the number of subnetworks and the number of neurons within each subnetwork.Note that the degraded impact of time-delayed coupling on bursting synchronization may have potential theoretical significance for curing some neuronal diseases(such as Parkinson's Disease,epilepsy)caused by bursting synchronization.
modular neuronal network, bursting synchronization, hybrid synapses, time-delayed coupling
15 December 2014,
4 January 2015.
10.6052/1672-6553-2015-007
2014-12-15 收到第 1 稿,2015-01-04 收到修改稿.
*国家自然科学基金(11272258,11572180)、中央高校基本科研业务费专项资金(GK201302001)、陕西省自然科学基础研究计划(2014JQ1013)资助项目
E-mail:yangxiaoli@snnu.edu.cn
