深水钻井隔水管涡激振动特性的数值模拟研究
2015-09-15王嘉松蒋世全许亮斌上海交通大学船舶海洋与建筑工程学院上海0040中海油研究总院北京0008
王嘉松 蒋世全 许亮斌(.上海交通大学船舶海洋与建筑工程学院,上海 0040; .中海油研究总院,北京 0008)
深水钻井隔水管涡激振动特性的数值模拟研究
王嘉松1蒋世全2许亮斌2
(1.上海交通大学船舶海洋与建筑工程学院,上海200240; 2.中海油研究总院,北京100028)
深水钻井隔水管作为深水油气开发的关键部件必然面临涡激振动及其疲劳损坏这一重大安全问题,正受到广泛关注。基于精细流场模拟并耦合结构动力响应的流固耦合方法是准确分析隔水管涡激振动特性的必然趋势。文中总结了“十一五”期间和正在进行的“十二五”课题在数值模拟方面的部分研究成果,针对简化的和实际尺寸的隔水管所涉及的涡激振动问题,提出高精度流固耦合分析技术,建立了隔水管涡激振动分析可靠的物理模型、数学模型和数值模拟方法。通过对比实验验证了模型的可靠性。基于简化和实际情况下(海况、结构、尺寸等)钻井隔水管涡激振动进行了大量的数值模拟研究,给出了高雷诺数下具有实际海况的几种典型洋流条件,如剪切流、亚临界和临界流条件下实际尺寸隔水管的涡激振动特性,以及顶部张力控制隔水管涡激振动的效果。
钻井隔水管;涡激振动;流固耦合;高雷诺数;剪切流;顶部张力;数值模拟
被视作连接钻井平台和海底井口通道的“咽喉”的深水钻井隔水管,对于保障海洋油气勘探开发正常运行具有重大作用。已投入使用的3 000 m水深10 000 m钻深的“海洋石油981”钻井平台在运行过程中必然面临隔水管的安全问题,其中涡激振动(VIV)及其诱发的疲劳损坏是最关键的问题。隔水管涡激振动的机理、预报和控制在科学界被视为一大难题,如何设计、运行、维护和保护隔水管也是工程界必须解决的重要问题,正在受到广泛关注。
深水钻井隔水管本质上属于大长径比、由不同接头连接的、中空的、带有附属管线和浮力块、以钢材为主的圆柱体,是从钻井平台转盘面以下到海底井口的管柱组合,包括分流器、上部挠性接头、短节、伸缩节、填充阀、适配器、不同壁厚和管径的隔水管单根/浮力块(含附属管线)、底部总成、下部挠性接头的组合,再连接到海底井口防喷器形成外阻洋流内保钻柱和钻井液,上连平台下连海底的纽带和通道。因受海洋波流的长期冲刷,雷诺数高达104~106,诱发的涡激振动不可避免。随着水深增加,产生涡激振动并疲劳破坏的几率加大。2H、NDP、SHELL、BP等国际著名的石油公司都监测到其在墨西哥湾、西非、挪威、巴西等海域使用的隔水管存在涡激振动现象。过去20年来,国际上采用了大量的模型实验来研究隔水管发生涡激振动的机理和控制措施,其中螺旋型(Helical Strakes)[1]隔水管是最流行的一种。SHEAR7、VIVANA等[2-3]是国际上流行的涡激振动工程分析软件,其流体力学模型来源于水深大多在数十米以内的实验,与深水相比,存在尺度上的巨大差异。另外,它们也不能提供来流方向(曳力)的分析。基于精细流场模拟并耦合结构动力响应的流固耦合方法是准确分析隔水管VIV特性的必然趋势。
深水钻井隔水管受到的外载复杂,包括重力、浮力、张力、内压力、压差力(曳力、升力)、平台运动的惯性力和附加质量力和力矩等。风浪对平台也对隔水管本身有间接影响,平台的运动对隔水管还有耦合作用。从研究现状来看,隔水管VIV问题依赖于圆柱绕流问题的流体力学分析,较少针对隔水管直接进行VIV问题研究,大多是圆柱VIV问题的推广应用。3 000 m钻井隔水管长径比可达5 000~ 10 000,属于典型的细长圆柱结构,即使不考虑附属管线等复杂结构及其组合,本身也是三维问题,但针对深水隔水管的VIV问题在国内外甚少有报道,可能一方面在于问题本身的复杂性和困难,另一方面,长细结构流固耦合需要的计算量特别巨大,非一般的计算条件所能承受。因此,要准确可靠地分析隔水管的VIV特性,需要建立准确可靠的理论模型、数值模拟方法,涉及物理问题的准确描述、各种条件的可靠设置、并行计算的高效设计、大变形问题的恰当处理等。
总结了在数值模拟方面的部分研究成果,针对实际尺寸隔水管的涡激振动问题,提出高精度流固耦合分析技术,建立了隔水管VIV分析的物理模型、数学模型和数值模拟方法。基于实际情况下钻井隔水管VIV特性进行了数值模拟研究,验证了模型的可靠性,分析了隔水管的二维和三维VIV产生机理和流固耦合及其振动特性。
1 物理模型、数学模型及研究方法
隔水管产生涡激振动的主要来源是海洋洋流,流向产生曳力作用(主要由柱体前后脉动压差和表面摩擦力引起),横向产生升力作用(主要由柱体两侧产生脉动压差和表面摩擦力引起),形状变化导致流动分离和涡的非对称脱落泄放,当流动诱发涡泄频率接近隔水管系统的固有频率时,易产生涡激共振,导致失稳和疲劳破坏。其主要特征是多维、非线性、自激、多模态且多自由度。如果结合隔水管的其他受力,如波浪、内流、顶部张力、平台的耦合、洋流的梯度变化、内波等作用,深水钻井隔水管VIV问题将异常复杂。因此隔水管VIV研究的模型常常做一定的简化。比如,把隔水管概化为中空有壁厚的圆柱,把三维简化为二维,把不同直径简化为单一等效直径,把流固耦合简化为弱耦合或不耦合,以结构力学为重点把流体力学模型简化为经验模型,以流动力学为重点只研究流体力学或水动力学特征。迄今大多集中于圆柱涡激振动的机理研究,远未达到实际工况的状态。从已发表的文献来看,未有针对实际尺寸深水隔水管基于流固耦合研究VIV的报道。本研究课题组一方面进行了简化模型的VIV机理及其控制研究;另一方面尽可能向几何和结构参数及环境条件趋向实际的钻井隔水管靠近,以揭示实际隔水管和海况下的VIV机理及其抑制机制。
由上述可知,钻井隔水管VIV问题非常复杂,但可以从不同的研究手段上展开。
在模型实验方面,现场实验影响因素太多且不可控因素多,代价昂贵难于实际开展研究,财力雄厚的2H、MARIN等公司对VIV进行了不少现场监测,反映了VIV的实际存在及其抑制效果。通常是进行室内模型如水池、水洞和风洞实验研究[4-6],涉及流动、振动、受力等方面的可靠测试分析手段。这种研究一定是小模型、机理性的研究,虽较难直接推广到实际工况,但对于实际工况具有很好的指导作用。
在理论与数值模拟方面,涉及流体力学与结构力学2个学科的结合,数学模型需要准确可靠和高效,在数值模拟方面需要高精度的流动分析方法和结构动力学响应的分析方法。大长径比问题中需要可靠的针对大位移、大变形、动网格等问题的手段。相对来说,结构动力学响应的模型和求解比较成熟,流体动力学的模型和求解方法较多,需要在精度和效率上综合考虑。本研究所采用的流体动力学模型及其求解方法主要是2个方面:一是基于雷诺平均的Navier-Stokes方程结合优选的湍流模型,采用笔者多年来发展的高精度高分辨率有限体积算法[7];二是基于涡量-流函数方程,采用发展的离散涡方法结合切片法[8]。从二维发展到三维,从单一管柱发展到复合管柱,从梁结构发展到实体结构,从低雷诺数发展到实际的高雷诺数,从浅水发展到深水。
在工程应用方面,需要发展快速可靠的VIV分析软件,国际上已有不少,如SHEAR7/VIVA/VIVANA|等[2-3],但它们一方面只针对垂直于来流方向即横向(cross-flow)的动力学分析,而无顺流向(in-line)的动力学分析及在2个方向的综合作用分析;另一方面,软件所涉及的流体升力模型基于模型实验尺度,用于实际深水在精度方面不可避免会降低。因此提出了尽可能考虑实际工况,基于采用计算流体动力学(CFD)和流固耦合(FSI)所获得的基础数据为流体升阻力模型,开发了VIV分析软件。
但限于篇幅,本文仅从基于流固耦合数值模拟角度分析隔水管VIV特性。
2 隔水管VIV特性的数值模拟研究
2.1算法及其可靠性验证
高分辨率算法的典型代表,TVD类格式在气动力学中取得了巨大成功,在浅水间断问题中也有很好的应用[7-8]。近几年来笔者开始将这类格式应用于一般的不可压缩流动问题,对规则网格所建立的有限差分TVD算法反映了良好的数值性能[9]。为了很好地利用TVD格式解决圆柱绕流这样的不规则边界问题,首次提出了速度向量分解(EVVT)方法[10],从而可以避免求解复杂的基于曲线坐标系的方程组。利用拟可压缩方法,同时采用双时间步方法对时间导数项离散。虚拟时间项进行内迭代,直到虚拟时间项趋向于一个小量(视为接近于0),满足不可压缩流的连续性方程,利用真实时间步长进行时间推进,获得参量的瞬态结果;利用TVD格式获得空间单元及其卫星单元间数值通量;对湍流模型进行优选,表明重整化群(Renormalisation Group, RNG) 模型结果更好[9]。最终建立起基于有限体积的TVD格式的绕隔水管层流和湍流流动的高精度数值模拟算法[11],精度与传统算法相比有显著提高,反映了该算法良好的数值性能。然后耦合结构动力学模型,以得到FSI模型[12]。对于隔水管振动的结构动力学响应模型,简化为质量(m)-阻尼(ξ)-弹簧(k)振子系统。单自由度(1DOF)是仅考虑横向(垂直于来流方向)运动,两自由度(2DOF)系统则可以同时沿横向和流向运动。采用四步龙格-库塔法或欧拉法求解,同时与 CFD模型耦合,流动模拟提供流场压力场,对隔水管固体壁面积分得到任意时刻的升阻力,提供给动力学方程作为外力,求解动力学方程,获得新时刻的位移和振动速度。根据圆柱空间变化的位移和速度修改或新划分CFD网格体系,利用结构振动速度作为边界速度条件,和上时刻的结果作为初始条件,重新进行CFD模拟计算,进行迭代运算,获得满足进度的新时刻结果,依此重复上述步骤,获得流固耦合的VIV结果[12-13]。
对于三维问题,由于存在多自由度、多模态、强非线性、大变形、细长结构、动网格等复杂特性增加了处理的难度,目前用于实际工程的算例少见报道。本研究采用ANSYS独具特色的FSI流固耦合高级分析技术,以ANSYS和CFX两个模块为基础,通过先进的流固耦合算法实现结构分析和流体分析的双向耦合计算,提供了FSI问题完整的解决方案。耦合的关键在于不同场之间数据的无缝传递,特别是在CFD模型方面,对动网格、数值计算模型、湍流模型、网格局部加密等方法和技术上进行了优化研究,利用超级计算机多核并行计算获得实体三维隔水管VIV分析结果。总体上,计算与实验结果和Huang等(2009)利用大涡模拟(LES)数值模拟结果吻合较好[14]。
2.2弹性支撑二维隔水管VIV特性
在洋流均匀、管柱较短且振动均匀的情况下可以把隔水管简化为二维圆管,同时二维VIV特性也为三维VIV研究提供了重要的研究基础。
图1是根据国外(1996)实验条件[15]进行模拟的,涡激振动振幅随约化速度Ur变化的曲线。一方面反映出本研究的数值模拟模型的可靠性,另一方面揭示了涡激振动振幅随约化速度Ur的变化特征:呈现 “三枝”,从Ur=2.5到Ur=4.2的过程中,振幅快速增大至最高点,随着Ur的继续增加,在Ur=6左右出现突变,然后涡激振动振幅逐渐减少。当约化速度在4.5~7.0(固有频率与涡泄频率接近)时,发生频率锁定,振幅达到最大。两自由度二维圆柱涡激振动的轨迹,体现了典型的8字型特征,流向振幅小于横向振幅,最大振幅在频率锁定区。
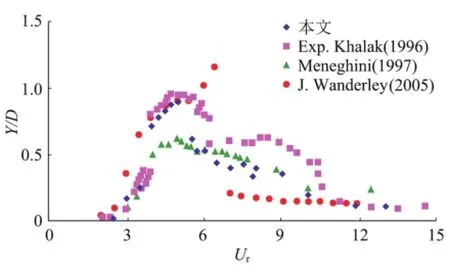
图1 涡激振动振幅随约化速度变化
为了研究质量比和阻尼比的影响,增加质量比分别为5 m*、10 m* (其中m* 是参考质量比),阻尼比分别为5 ξ、10 ξ, (其中ξ 为参考阻尼比)。研究表明,随着质量比的增加,振动幅值减小,且在频率锁定区更明显;随着阻尼比的增加,振动幅值略有减小,对幅值变化的影响相对较小。
对于实际尺寸的隔水管,选取隔水管参数如下,隔水管外径Do=0.533 4 m,内径Di=0.482 6 m,密度ρs=7 850 kg/m3,单位长度隔水管质量m=ρsπ(Do2–Di2)/4 =318.05 kg/m。由此可计算出质量比为1.42。设单根隔水管长度22.86 m,取9根隔水管,所以总长为205.7 m。由此可以计算出不计顶部张力时隔水管的一阶固有频率为0.034 8 Hz。
计算靠近振幅频率锁定附近,约化速度Ur=3.4~ 8.6,相当于来流速度U0=0.07~0.16 m/s,雷诺数35 000~85 000。模拟研究结果表明,隔水管的涡激振动规律,包括升阻力系数、频率比以及最大振幅变化规律与之前模拟结果所得到的规律一致,但远比固定情况下的值大,如阻力系数达到1.2~3.5,升力系数达到0.4到3.0。由于水的密度较大所以实际隔水管的涡激振动的质量比较小,X、Y方向振幅的最大值相应的也有所增加,隔水管X、Y方向的最大振幅大约在0.9以及1.3左右。
2.3隔水管三维VIV特性
图2为隔水管VIV分析模型示意图。其上部连接钻井平台,下部连接井口,两端铰支,上端还可施加顶部张力,水平方向受到洋流绕流泄涡引起的阻力和升力。
影响隔水管VIV的因素可归结为雷诺数、流向、流速、深度方向的流动梯度、管内流体、结构质量、阻尼、顶部张力、附属管线等。限于篇幅,这里给出几种典型工况或条件下的隔水管VIV三维特性。本研究所涉及的基本参数包括:隔水管外径Do=0.533 4m,内径0.482 6 m,密度7 850 kg/m3,单位长度隔水管质量318.05 kg/m,抗弯刚度2.62×108。

图2 隔水管VIV分析的简化模型
2.3.1剪切流和均匀流作用下的隔水管VIV分析[16]
隔水管的参数见表1。均匀流时速度0.8 m/s,雷诺数4.1×105,而剪切梯度流的最大雷诺数为7.69×105,除隔水管底端附近(z/L=0~0.3)外,流动处于典型的临界流动区域,入流条件见图3。

表1 模拟隔水管的参数
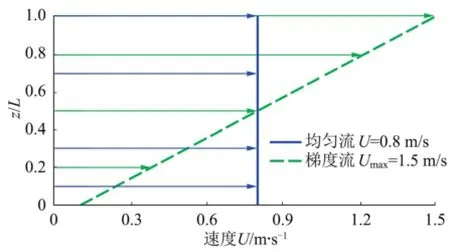
图3 两种入流条件
图4显示了隔水管涡激振动的过程及在不同流动截面 z/L=0.1、0.3、0.5、0.7、0.9上涡的泄放。图(a)、(b)、(c)是在均匀流作用下的结果,图(d)、(e)、(f)是在剪切流作用下的结果。对于均匀流隔水管的最大挠度发生在其中间截面,而对于剪切流其最大挠度发生在略高一点的位置,并且2种流动下隔水管的最大挠度基本相同都约为5D,这是因为剪切度流的平均速度正好等于均匀流的速度,而拖曳力与速度平方成正比。所以对于剪切流来说,隔水管的最大挠度基本取决于它的平均速度。
2.3.2不同洋流速度下隔水管的VIV特性针对长502.92 m、长径比943的隔水管分别在均匀流V=0.1m/s、0.5 m/s和0.8 m/s下的VIV 特性进行了模拟分析。
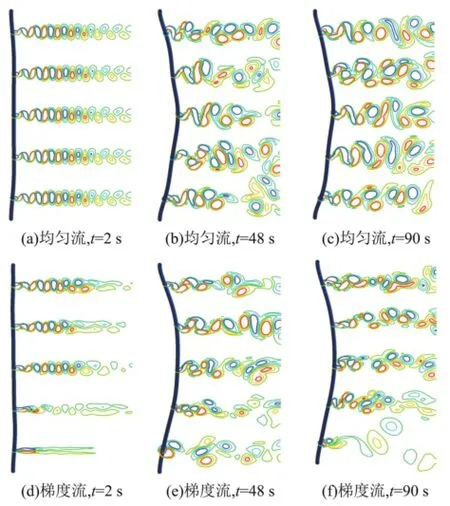
图4 涡泄模式及隔水管的响应历程
图5 表示2种洋流(左图对应V=0.5 m/s,右图对应V=0.8 m/s)下隔水管振动的时间历程以及涡泄模式,分别表示在t=60 s时隔水管的变形以及隔水管在z/L=0.1、0.3、0.5、0.7和0.9截面上对应的涡泄模式。隔水管的变形主要是由阻力决定的,也就是在顺流向隔水管会有更明显的变形,而升力的振动能量要比阻力大很多,所以在横流向隔水管会有更明显的周期性振动。同时,隔水管的振动曲线体现了多阶模态。涡泄模式随着隔水管的变形趋于复杂,出现了2P、P+S、2C等模式,且同一时间沿轴向不同截面上的涡泄模式也互不相同,但是各截面上涡的泄放也不是独立的,而是相互影响。
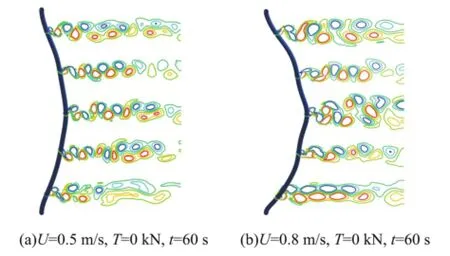
图5 隔水管的振动历程及其涡泄模式
隔水管整体的变形情况以及振动特性为,速度越大,振动的模态越高,且振幅值也越大。隔水管在横流向有更明显的周期性振动,速度越大,模态阶数越高,V=0.1 m/s下只出2阶模态,V=0.5 m/s下表现出了5阶模态,而V=0.8 m/s下的振动则表现得很不规律,不能直观看出有几阶模态;顺流向的振动并不比横流向的小,说明顺流向的振动也不可忽略,特别是对于这种大长径比的隔水管。
2.3.3不同顶部张力下隔水管的VIV特性针对长502.92 m、长径比943的隔水管分别在均匀流V=0.1m/s、0.5 m/s和0.8 m/s下不同顶部张力(0和2 000 kN)的VIV 特性进行了模拟分析。
可以得到,顶张力对于抑制隔水管在顺流向的变形是非常有效的,不过洋流速度越大,其抑制作用越小,在V=0.1 m/s时,2 000 kN的预紧力可以把顺流向的变形减少93.7%之多,在V=0.5 m/s 时,能减少57.1%,而对于V=0.8 m/s,只能减少36.5%。顶张力对于横流向变形的作用,取其均方根值来说明,顶张力对横流向变形的抑制作用也是随着来流速度的增大而减小。不过在V=0.5 m/s时,在顶张力的作用下,横流向的变形反常地出现了增大的情况。原因可能是预紧力使横流向振动的模态阶数减小。
3 结论
总结了近几年来在隔水管涡激振动数值模拟方面的部分研究成果。提出了高精度流固耦合分析技术,建立了隔水管涡激振动分析的物理模型、数学模型和数值模拟方法。通过对比实验验证了模型的可靠性。给出了高雷诺数下具有实际海况的几种典型洋流条件,如剪切流、亚临界和临界流条件下实际尺寸隔水管的涡激振动特性,以及质量比、顶部张力等对隔水管涡激振动特性的影响。
(1)为避免采用复杂的曲线坐标系和非结构化网格,在空间离散方案上首次提出了速度向量分解(EVVT)方法。该方法易于实现圆柱类不规则几何边界和其他任意四边形(六面体)网格的高精度离散格式的插值;采用新提出的EVVT技术、高精度的TVD格式和优选的湍流模型,使CFD计算结果更精确,在VIV分析方面,精度得到明显提高。
(2)涡激振动特性与约化速度、雷诺数、质量比、阻尼比等因素有关;二维涡激振动呈典型的8字形轨迹,三维涡激振动呈变型的8字形轨迹;当约化速度较小和较大时,运动轨迹的最大振幅较小;当约化速度在4.5~8.5时,频率比接近于1,运动轨迹的最大振幅较大。
(3)增大隔水管质量比、阻尼比和顶部张力都可以一定程度抑制隔水管的涡激振动。
(4)通过不同尺寸隔水管VIV的模拟表明,在洋流速度较小时,振动模态较少,振动形态相对简单;在洋流速度较大时,振动模态较多,振动形态变得复杂,尾流的三维效应、扭曲现象更明显。
(5)400 m长的隔水管在线性梯度流(V=0.1~1.5 m/s)作用下的涡激振动与相当于它平均速度的均匀流(V=0.8 m/s)相比较,梯度流在顺流向的挠度取决于它的平均速度,与平均速度下的均匀流基本相同,只是最大挠度发生在中间截面偏上一点的地方。在横流向2种流动都表现出3阶模态,梯度流下隔水管的振动更加复杂,振形没有明显的驻点,且挠度比均匀流下要大,特别是在中间截面上挠度比之均匀流时大了近50%;均匀流下隔水管的运动轨迹在两端都有比较明显的“8”字形,而梯度流下只在底部(z/ L=0.1),也就是速度小的一端才有很明显的“8”字形,而在中间部位及顶部都没有。
(6)500 m长的隔水管在不同速度均匀流(V=0.1 m/s、0.5 m/s、0.8 m/s)下的振动特性,隔水管发生涡激振动时的涡泄模式随来流速度的增大而表现得更加复杂;隔水管在顺流向的变形随来流速度的增大而增大,但是并没有与速度的平方成正比,而是近乎与速度的一次方成正比。来流速度越大,隔水管振动表现出的模态阶数越高,且振动越趋于复杂、不规则;其运动轨迹也是如此,在来流速度小(V=0.1 m/s)的时候,大多截面上的运动轨迹可以看出“8”字形,而随着速度的增大(V=0.5 m/s),只能在隔水管两端的运动轨迹上看出“8”字形,当速度再增大时(V=0.8 m/s),两端的运动轨迹也变混乱。
(7)顶部张力增加了隔水管的刚度及阻尼,对于隔水管顺流向的变形有很好的抑制作用,对横流向变形的抑制相对较小;对于隔水管的振动模态,顶部张力也有一定程度的抑制作用。
[1]PAOLOS, NEIL W. Investigation on vortex induced oscillations and helical strakes effectiveness at very high incidence angles[C]. The Ninth International Offshore and Polar Engineering Conference. 1999.
[2]VANDIVER J K, LI L. SHEAR7 V4.3 Program theoretical manual. department of ocean engineering massachusetts institute of technology[R]. 2003.
[3]LARSEN C M et al. VIVANA Theory manual [R]. MARINTEK 513102.01, Trondheim, Norway, 2000.
[4]SARPLAYA T. Vortex-induced oscillation, a selective review[J]. Journal of Applied Mechanics, 1979(46): 241-258.
[5]VANDIVER J K, MARCOLLO H. High mode number VIV experiments. IUTAM symposium on integrated modeling of fully coupled fluid-structure interactions using analysis, computations, and experiments[C]. Dordrecht: Kluwer Academic Publishers. 2003-06.
[6]GU Ffi, WANG Jiasong, QIAO Xinqi, HUANG Zhen. Pressure distribution, fluctuating forces and vortex shedding behavior of circular cylinder with rotatable splitter plates[J]. Journal of Fluids and Structures, 2012(28): 268-278.
[7]WANG J S, Ni H G, HE Y S. Finite-difference TVD scheme for the computation of dam-break problems[J]. ASCE Journal of Hydraulic Engineering. 2000, 126(4): 253-262.
[8]WANG J S, HE Y S,NI Han G. Free surface flow in branch channels by a finite-volume TVD scheme[J]. Advances in Water Resources, 2003, 26(6): 623-633.
[9]WANG J S. A two-dimensional TVD scheme for incompressible turbulent flows with pseudo-compressibility method[J]. Progress in Computational Fluid Dynamics, 2009, 9(2): 86-95.
[10]WANG Jiasong. Flow around a circular cylinder using a finite-volume TVD scheme based on a vector transformation approach[J]. Journal of Hydrodynamics, 2010, 22(2): 221-228.
[11]王嘉松. 圆柱绕流的高分辨率有限体积数值模拟方法[C].全国力学大会,郑州,2009.
[12]WANG Jiasong, LIU Hua, JIANG Shiquan, et al. Vortexinduced vibration on 2D circular riser using a high resolution numerical scheme[C]. Proceedings of 9th International Conference on Hydrodynamics, 2010, October 11-15, Shanghai, China, 954-959.
[13]赵鹏良,王嘉松,蒋世全,等. 海洋立管涡激振动的流固耦合模拟计算[J].海洋技术,2010,10(3): 73-77.
[14]王成官,王嘉松,田中旭,等. 海洋隔水管涡激振动的三维数值模拟研究[J]. 水动力学研究与进展,2011,26(4):437-443.
[15]KHALAK A, WILLIAMSON C H K. Dynamics of a hydroelastic cylinder with very low mass and damping[J]. Journal of Fluids and Structure, 1996(10): 455-472.
[16]WANG Jiasong, ZHAN Lulu, JIANG Shiquan, et al. Numerical simulation of VIV for a marine riser in uniform and linearly sheared currents[C]. The 23rd International Offshore (Ocean) and Polar Engineering Conference, Anchorage, Alaska, USA, June 30-July 5, 2013.
〔编辑薛改珍〕
Numerical simulation of drilling riser vortex induced vibration characteristics in deepwater
WANG Jiasong1, JIANG Shiquan2, XU Liangbin2
(1. School of Naval Architecture, Ocean & Civil Engineering of Shanghai Jiao Tong University, Shanghai 200240, China; 2.Research Institute of CNOOC, Beijing 100028, China)
Offshore oil and gas exploration and development are undergoing a strategic shift to deep and ultra-deep waters. As a critical part of deepwater oil and gas development, deepwater drilling riser will surely be confronted with the major safety problem of vortex induced vibrationg(VIV), and fatigue failure and it is attracting widespread attention. Fluid-structure coupling based on refined flow field simulation with coupled structural dynamic response is an inevitable trend to accurately analyze the VIV characteristics of riser. This paper summarizes some of the research results on numerical simulation during the “Eleventh Five-Year” period and the ongoing research projects in the “Twelfth Five-Year” period. To address the VIV problems of risers in simplified and practical sizes, a high-precision fluid-structure coupling analysis technology is proposed, and reliable physical model, mathematical model and numerical simulation are built for analysis of riser VIV. The comparative experiment verifies the reliability of the models. The large number of numerical simulation researches on the VIV of drilling riser under simplified and practical cases (sea conditions, structure, size, etc.) show the VIV characteristics of riser with practical size under several typical ocean currents with a high reynolds number high under actual sea conditions, such as shear flow, subcritical flow and critical flow, as well as the controlling effect of top tension on the VIV of riser in some way.
drilling riser; vortex induced vibration; fluid-structure coupling; high reynolds number; shear flow; top tension; numerical simulation
TE21
A
1000 – 7393(2015) 01 – 0030 – 06
10.13639/j.odpt.2015.01.007
国家科技重大专项子课题“深水油气田开发钻完井工程配套技术”(编号:2008ZX05026-001,2011ZX05026-001);国家自然科学基金“深水隔水管涡激振动抑制装置的高精度流固耦合模拟研究”(编号:51079084)。
王嘉松,1967年生。1998年获大连理工大学水工结构工程博士学位,现从事流体力学、流固耦合力学及流动控制等方面的教学与科研工作,教授,博士生导师。电话:021-34205311。E-mail: jswang@sjtu.edu.cn。
2014-12-31)
引用格式:王嘉松,蒋世全,许亮斌. 深水钻井隔水管涡激振动特性的数值模拟研究 [J].石油钻采工艺,2015,37(1):30-35.
