某电子设备的天线罩和涂层热膨胀匹配研究
2015-09-15陈正江
陈正江,黄 巍,杨 伟
(中国电子科技集团公司第三十研究所, 四川 成都 610041)
某电子设备的天线罩和涂层热膨胀匹配研究
陈正江,黄 巍,杨 伟
(中国电子科技集团公司第三十研究所, 四川 成都 610041)
为了提高某电子设备的天线罩在高温环境下工作的可靠性,确保涂层不脱落,文中结合工程实际,利用ANSYS建立参数化有限元模型,对天线罩及表面涂层进行瞬态分析及热-结构耦合分析,得到天线罩温度与时间的关系及涂层粘接面剪切应力与时间的关系。根据涂层发生脱落时的最大剪切应力对涂层的热膨胀系数进行参数化编程计算,确定了涂层的热膨胀系数范围,为选择匹配的天线罩涂层提供了理论依据,保证涂层在一定温度与一定时间内不开裂脱落。
天线罩;涂层;ANSYS;热膨胀;匹配
引 言
长时间处于高温工作环境下的电子设备作为技术含量极高的工业产品,对耐高温涂层的性能指标和质量的要求日趋严格,而涂层质量的优劣除了体现在其自身产品质量的好坏之外,还体现在其与基体材料相结合、相匹配的程度上。近年来国内外在涂层与此类设备之间的结合机理、热应力变化、新型涂层材料等方面进行了研究,以提高涂层与设备的结合性能[1-3]。但是目前在涂层与设备相互匹配性方面的研究较少,而电子设备的天线罩表面涂层对天线的透波能力和隔热能力有直接影响。在高温环境下工作时,天线罩和涂层会同时受到热辐射、传导、对流等作用而发生热膨胀。当涂层与天线罩结合界面的剪切应力超过粘接强度时,涂层可能开裂甚至脱落,造成天线罩失去涂层保护,使设备工作不正常、不可靠。本文研究的主要目的在于找出涂层与天线罩之间的热匹配数据,从而确定安全条件下的涂层热膨胀系数范围,保证设备能够可靠工作。
1 分析基础及失效评定准则
1.1 分析基础
本文主要针对天线罩温度场及应力场进行分析,确定涂层热膨胀系数合理范围。其中热分析分为稳态热分析及瞬态热分析。稳态热分析的温度向量{T}通过下面的矩阵方程解得:
K(T)·T=Q(T)
(1)
式中:K传导矩阵,包含导热系数、对流系数及辐射率和形状系数;T为节点温度向量;Q为节点热流率向量。
瞬态传热过程指一个系统的加热或冷却过程,其中系统的温度、热流率、热边界条件及系统内能随时间都有明显的变化。根据能量守恒原理,瞬态热平衡可以表达为:

(2)
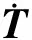
1.2 失效评定准则
通过热应力耦合仿真得到零件与涂层之间的粘接面剪切应力随时间变化的曲线,以此来判断整个过程中是否会达到极限粘接强度。当超过极限粘接强度时,就会发生涂层脱落的现象,判定为涂层失效。
2 结构有限元模型
2.1 几何模型
设备由石英陶瓷天线罩和隔热表面涂层组成,涂层依靠自身粘合力附着在陶瓷材料上表面。天线罩圆盘底部直径为120 mm,半球形球面顶部直径为100 mm,罩体平均厚度为8 mm,涂层厚度约为3 mm。为实现涂层的热膨胀系数等值的参数化,利用ANSYS DesignModeler模块建立三维模型。实际中涂层未脱离时与天线罩之间不存在相对位移,可以认为两者固联且无相对滑动,因此在ANSYS中对涂层与石英陶瓷之间采用绑定(bond)接触,两者之间不会产生分离。同时为了得到受热膨胀后的剪切应力,接触方程采用拉格朗日方程,非对称接触。在接触面与目标面的选取上,将材料偏软的零件设置为接触面较为合适,因此选择涂层一侧的界面为接触面,最终接触的结果也将在这一侧显示,如图1所示。

图1 天线罩模型
2.2 材料数据
天线罩基体材料为石英陶瓷,表面涂层为具有隔热性能的非金属材料,常温下石英陶瓷和涂层材料特性见表1,在ANSYS中通过直接定义方式添加新材料并设置相应的材料参数。

表1 材料特性表
3 有限元热仿真计算
本文研究中热分析单元采用SOLID70,用于计算温度分布;结构单元使用SOLID185,用于计算结构的应力分布;接触面单元采用CONTA174、TARGE170,用于计算粘接面应力。利用ANSYS多区域扫掠方法进行自动区域划分后得到完全六面体网格,同时保证网格质量,如图2所示。

图2 有限元网格模型
外界环境温度由20 ℃上升至300 ℃,温度-时间梯度为4.7 ℃/s,60 s后达到300 ℃,之后环境温度基本保持不变。设备与环境的热交换主要通过对流方式实现,分析中建立的对流方程为:
q=hA(Tsurface-Tambient)
(3)
式中:q为对流热量;h为对流系数,计算中取常用的空气对流系数5 W/(m2·℃);Tsurface为零件对流表面的温度;Tambient为环境温度。
温度变化曲线如图3所示,在环境温度上升过程中,天线罩温度变化与时间成正比,同时,天线罩最高温度比环境温度滞后4 s左右达到相同。当60 s时刻环境温度到达300 ℃,整个结构已经接近环境温度,此后温度维持在300 ℃不变,温升达到稳态。

图3 温度-时间曲线
选取60 s时刻的温度分布如图4所示,天线罩顶部到底部温度逐渐降低,表明热流主要从天线罩底部与安装架连接部位向外传导。

图4 温度分布
通过ANSYS中多场耦合分析,将前一个物理场分析的结果作为后一个物理场分析的输入条件进行计算,即将上述所有时刻点的温度分布结果输入到结构分析中进行热-结构耦合分析,如图5所示。
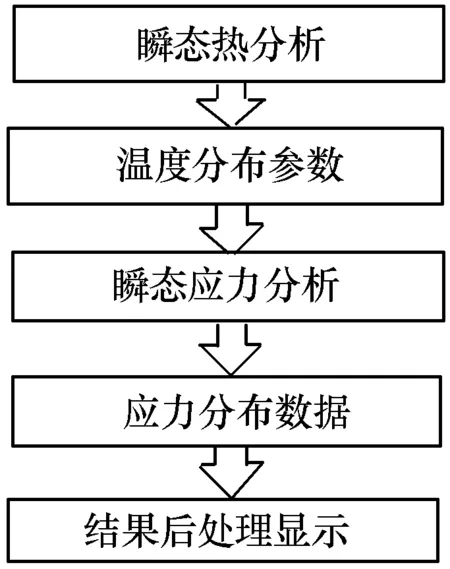
图5 热-结构耦合分析步骤
粘接面最大剪切应力随时间变化曲线见图6。
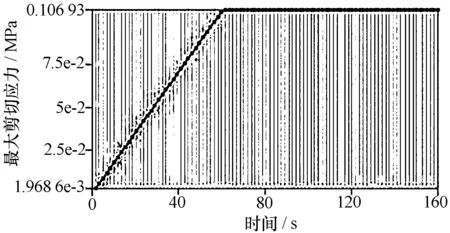
图6 粘接面最大剪切应力变化曲线
选取60 s时刻的粘接面剪切应力分布见图7。

图7 剪切应力分布
粘接面的剪切应力在整个过程中呈现线性变化。当环境温度到达300 ℃后,天线罩结构呈现稳态,粘接面剪切应力达到最大值,涂层最易出现开裂脱落现象。
4 涂层热膨胀系数参数化分析
为了获得安全条件下涂层的热膨胀系数范围,需要将涂层的热膨胀系数参数化,以确定其与粘接面剪切应力之间的函数关系,从而得出当粘接面剪切应力在1 MPa(粘接强度)时热膨胀系数的取值范围。
本文通过ANSYS APDL参数化设计语言对涂层的热膨胀系数进行参数化编程,部分命令流如下:
!*******建立参数*******
thickness=3e-3 !隔热层厚度
diameter=100e-3
h1=31.5e-3
h2=40.3e-3
rad=6e-3
dens1=410 !涂层密度
dens2=1650 !石英陶瓷密度
alpx1=1.46e-6 !涂层热膨胀系数
alpx2=1.5e-6 !石英陶瓷热膨胀系数
c1=0.94 !涂层比热
c2=0.91 !石英陶瓷比热
ex1=5.3e8 !涂层弹模
ex2=1.8e10 !石英陶瓷弹模
!******定义材料参数*******
/prep7
mp,ex,1,ex1 !调用参数建立材料模型
mp,prxy,1,prxy
mp,dens,1,dens1
mp,kxx,1,kxx1
mp,c,1,c1
mp,alpx,1,alpx1
将涂层热膨胀系数设置为输入参数,将整个导热过程中粘接面最大剪切应力作为输出参数。设定涂层热膨胀系数的范围为1×10-8~4.5×10-6m/K,采用中心复合差分法选取在设定区域内的样本点,程序通过样本点计算输出参数的取值,如图8所示。

图8 样本点结果
得到样本点后,利用ANSYS DesignXplorer响应面分析可以得到输入参数和输出参数之间的函数曲线,采用完全二阶多项式法拟合函数关系,如图9所示。

图9 输入输出参数曲线
从图中可以看到,由于石英陶瓷材料的热膨胀系数为1.5×10-6m/K,当涂层的热膨胀系数接近石英陶瓷材料热膨胀系数时,粘接面剪切应力较小,越远离则应力越大,两者的匹配性越差。同时,当涂层的热膨胀系数小于3.7×10-6m/K时,粘接面的最大剪切应力小于1 MPa,属于安全范围,在使用过程中不易出现开裂失效。
5 结束语
本文研究分析了在特定高温环境下,天线罩和涂层受热膨胀后发生内部结构和应力变化,导致涂层脱落的过程。利用ANSYS准确构建分析模型和定义边界条件,选择合理的分析方法,确定了涂层的热膨胀系数范围,为天线罩和涂层在特定温度下的变化情况提供了详细的分析数据,有利于设计者了解具体情况并正确选择与天线罩匹配的涂层,保证涂层在一定温度与一定时间内不开裂脱落,设备工作可靠。
[1] 刘海定, 曹旭东, 贺文海, 等. 吸波涂层界面结合机理(I):涂层力学性能影响因素分析[J]. 功能材料, 2007, 38(7): 1045-1048.
[2] 李金龙, 熊化兵, 罗俊, 等. 气密性陶瓷封装内热应力的ANSYS分析[J]. 微电子学, 2012, 42(1): 130-133, 140.
[3] 郑蕾, 郭洪波, 郭磊, 等. 新一代超高温热障涂层研究[J]. 航空材料学报, 2012, 32(6): 14-24.
[4] 赵敦殳. 电子设备热设计[M]. 北京: 电子工业出版社, 2009.
[5] 杨志刚, 胡振东. 冷却器在瞬态工况下的温度场与热应力分析[J]. 计算机辅助工程, 2013, 22(1): 33-36.
陈正江(1977-),男,工程师,主要从事电子装备结构设计及仿真分析工作。
Research on Thermal Expansion Matching of Radome and Coating for an Electronic Equipment
CHEN Zheng-jiang,HUANG Wei,YANG Wei
(The30thResearchInstituteofCETC,Chengdu610041,China)
In order to improve the functional reliability of the radome of an electronic equipment in high-temperature environment and ensure that coating will not shed, this paper creates parametric finite element model by ANSYS and carries out transient state analysis and thermal-structural coupling analysis for radome and coating with engineering practice considered. Relationships between radome temperature and time, shearing-stress of bonding surface of coating and time are obtained. Based on the maximum shearing-stress of coating when it is shedding, the coefficient of thermal expansion is calculated by parametric programming and its range of value is determined. It provides theoretical foundation for choosing matching radome coating and make sure that coating will not shed and split in certain temperature range and certain period of time.
radome; coating; ANSYS; thermal expansion; matching
2014-12-31
TN820.8+1
A
1008-5300(2015)02-0055-04
