混入粗颗粒对移动床中空腔的抑制效应

许鹏凯，段学志，钱 刚，周兴贵

混入粗颗粒对移动床中空腔的抑制效应

许鹏凯，段学志，钱 刚，周兴贵

华东理工大学化学工程联合国家重点实验室，上海 200237

采用离散元方法（DEM）研究了粗颗粒的混入对移动床中空腔的抑制效应。结果表明，向移动床中混入粗颗粒能够抑制空腔的形成，尤其是在粗颗粒的壁面摩擦系数较小的情况下。为了进一步强化混入的粗颗粒对空腔的抑制效应，在粗颗粒与细颗粒的壁面摩擦系数相同时，应将粗颗粒分散在床层中，而对于粗颗粒壁面摩擦系数远小于细颗粒壁面摩擦系数的情况，应将其集中在壁面附近。

空腔 粒径 重力传递 空间分布 壁面摩擦系数 离散元方法

错流移动床具有颗粒可重复使用和操作压降低等优点，因而被广泛应用于多种化工生产，如丙烷脱氢［1］和催化重整［2］等。然而，在移动床操作过程中，空腔的形成可造成气体的分布不均匀，甚至短路，从而使移动床的操作过程恶化［3］。研究者通过分析床层中的应力分布以预测空腔的形成情况［3-7］。此外，陈允华等［8］还研究了锥形和Binsert整流子的引入对空腔的影响，其结果表明，这两种整流子的引入都能够推迟空腔的形成，尤其是在整流子靠近上游面时，该方法从移动床设计的角度抑制了空腔的形成。通过改善颗粒的性质，如增大粒径或减小颗粒与壁面之间的摩擦系数，也能够增大形成空腔的临界条件［3］。然而，在实际情况下，催化剂等颗粒的性质往往受到反应等因素的限制而难以改变。作为一种替代方法，向床层中混入一些与原有颗粒不同的颗粒，如粒径较大或壁面摩擦系数较小的颗粒，也有利于抑制空腔的形成，但目前尚未有研究者对其作用机制进行研究。

在对颗粒系统的研究中，离散元（DEM）方法已被广泛应用［9-12］。采用该方法能够获得与实际情况吻合较好的结果［10，13］，并能模拟空腔中单颗粒的运动行为，且易调整颗粒性质，并获得颗粒与壁面间作用力的变化情况，从而判断床层中空腔的形成情况。本工作采用DEM方法研究了场力作用下移动床中的空腔现象，并通过向床层中混入粗颗粒有效抑制了空腔的形成。为了进一步强化这一抑制效应，还研究了粗颗粒在床层中的空间分布及其壁面摩擦系数对空腔形成过程的影响。

1 计算方法

1.1 DEM方法

DEM方法最早由Cundall等［14］提出，其计算过程主要包含4个步骤：颗粒系统的生成，颗粒之间以及颗粒与壁面之间碰撞的搜索，碰撞作用力的计算以及颗粒运动状态的更新［15］。本工作中颗粒之间以及颗粒与壁面之间的作用力均通过线性模型计算［16］。更新颗粒的运动状态时，需要对颗粒的线性运动及转动进行更新，这两种运动分别可用方程（1）和（2）描述：

采用3D矩形截面的床层，其结构和尺寸如图1（a）所示，床层的宽度和高度分别为0.162 和1.04 m，厚度为0.027 m，且在前后面上采用周期边界条件。颗粒自底部出料口流出床层以后，重新从顶部进料口进入床层。颗粒的循环速率（R）等于颗粒从床层中流出的速率。出料口和进料口均位于床层中心轴线上，宽度分别为0.03 和0.04 m。床层半锥角为60°。

图1　移动床的结构以及3种床层中的颗粒空间分布Fig.1 Geometry of moving bed and space distribution of particles in three systems

图1（b）～（d）为本工作所研究的3种颗粒流动体系。其中蓝色颗粒代表细颗粒，粒径为4 mm；红色颗粒代表粗颗粒，粒径为8 mm。图1（b）所示体系中只有细颗粒，（c）和（d）所示体系中都混入了粗颗粒，其中，（c）所示体系将粗颗粒分散在床层中，（d）所示体系将粗颗粒集中到壁面附近。

颗粒的其他性质见表1。在设置颗粒性质时，本工作参考了Kruggel-Emden等［16］所用聚乙烯颗粒的性质。忽略了颗粒之间以及颗粒与壁面之间碰撞时的切向阻尼效应，故而将这两种碰撞的切向阻尼系数设为0。此外，在采用DEM研究颗粒流动时，研究者所选取的颗粒间摩擦系数一般不大于1.6［17］，所选取的颗粒与壁面间摩擦系数一般不大于1.0［18］。本工作中颗粒之间以及颗粒与壁面之间的摩擦系数也在上述范围内。

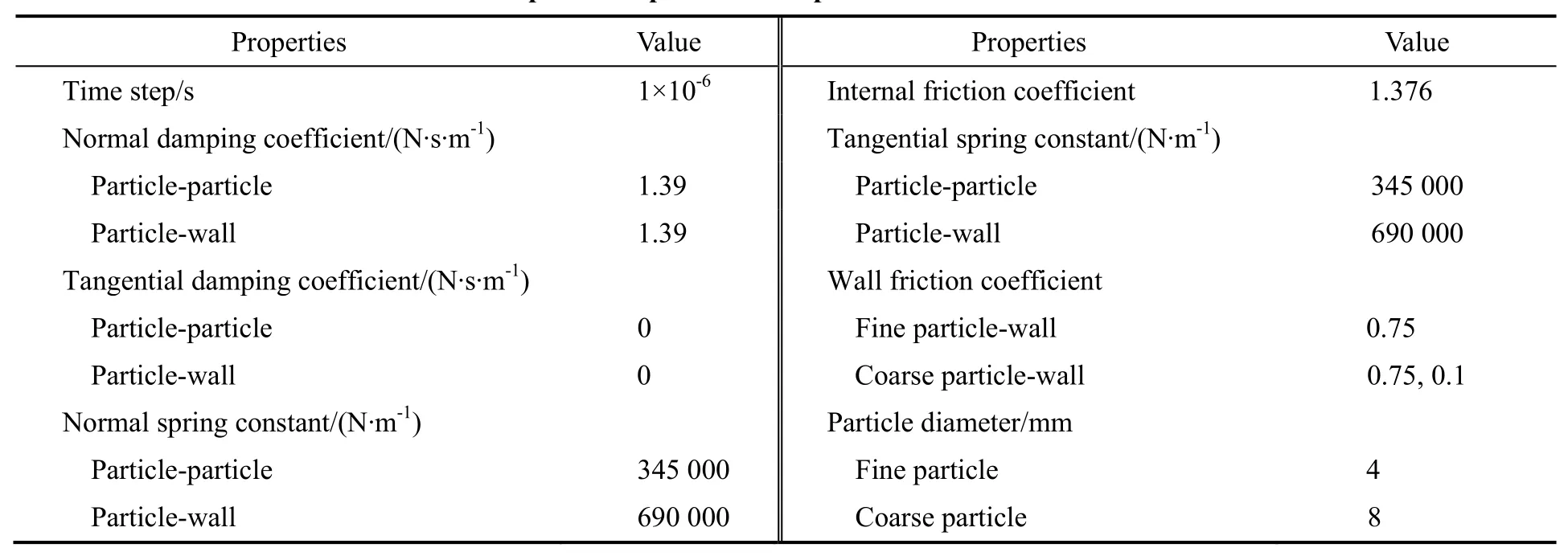
表1　计算过程中的颗粒物性及相关参数Table 1 Properties of particles and parameters used in simulation

1.2场力的计算

在移动床中，随着流场的增强，颗粒所受到的曳力也逐渐增大，进而使床层中形成空腔。若这些颗粒为带电颗粒，将流场替换为电场时，电场的增强同样能够增大颗粒所受到的场力，进而使得床层中形成空腔。相对于曳力来说，电场力的计算较为简单，进而可以减小计算负荷。因此，本工作采用电场来代替流场以研究床层中的颗粒流动。

为了使电场下所得结果能较好地反映流场下移动床中的颗粒流动情况，提出了几点假设。首先，假设粗颗粒和细颗粒所带电荷与颗粒的表面积成正比，分别为10和2.5 pC，且在颗粒碰撞时无电荷转移，此时，随着粒径的增大，颗粒所受电场力也增大。同时由于颗粒重力与颗粒的体积成正比，使颗粒所受电场力与颗粒重力之间的比值减小。在流场中增大颗粒粒径时，颗粒所受曳力以及曳力与颗粒重力之间的比值也发生相同的变化［19］。其次，假设颗粒所带电荷均集中于球心处，该假设使得带电颗粒几乎不受库仑力的作用，只受重力、场力以及碰撞时的作用力的影响，与流场中颗粒的受力情况一致。此外，在床层中形成明显的空腔之前可将流场视为均匀流场［3］。由于本工作并未考察床层中形成明显空腔时的情况，因此还假设电场为匀强电场以进一步降低计算负荷。采用以上假设所建立的电场反映了简化后的流场，故而相对于真实流场来说并不精确。然而，正如简化流场对于研究空腔并无影响一样［3］，采用该电场代替真实流场对于定性研究移动床中空腔的形成过程也无影响。

颗粒所受电场力用方程（3）计算：

电场在距床层底部0.1～0.4 m的区域内产生作用，如图1（a）中虚线所示区域，方向为自左向右。因此，所用床层，左侧壁面为上游面，而右侧壁面为下游面。

1.3 对空腔的确定

在外加场作用下，若一定高度范围内无颗粒与壁面接触可以认为床层中形成了空腔。然而，需要注意的是，即使无外加场的作用，颗粒也能与壁面分离。例如，在颗粒重力向壁面传递的过程中，壁面附近的颗粒可能对壁面上的颗粒进行挤压，使这些颗粒彼此分开，并造成一定高度范围内无颗粒与壁面接触。为排除这一情况，在判断床层中空腔的形成情况时，所选取的高度范围不应小于大颗粒直径的2倍。因此，若床层中存在高度不小于0.02 m的区域满足其中所有的颗粒均与上游面脱离，即认为形成了空腔。

为了更直观地表示床层中是否存在空腔，将上游面附近的区域（x为0～0.015 m）沿高度方向划分成若干高度为0.02 m的子区域，并考察该子区域的状态（S0），对于一个子区域来说，若其中所有颗粒均与上游壁面脱离，即认为该子区域内形成了空腔，并将这一状态记为-1；反之，则认为这一子区域内无空腔，并将这一状态记为1。当以上子区域中有一个或多个子区域内形成空腔，即认为床层中形成了空腔。此外，根据目前的研究结果［6，8］，空腔常形成于场力作用的区域内。因此，本工作中仅给出该区域内上游面附近的颗粒流动情况。

2 结果与讨论

2.1 细颗粒体系中的空腔现象

图2给出了细颗粒体系中，电场强度对颗粒流动的影响。图中彩色颗粒为示踪颗粒。这种颗粒与其他颗粒除颜色不同外，其他性质均相同。从图中可以看到，随着电场的增强，上游面附近逐渐形成空腔。此外，场力作用一段时间（2.0 s）后的示踪颗粒分布情况表明，在较强的电场下（如E为480 MN/C），上游面附近的颗粒流动明显快于下游面附近的颗粒流动。以上结果均与文献中流场作用下的实验结果一致［6，8，20］。从上游面应力分布（图 3）的结果中可以看到，场强的增大逐渐削弱了电场作用区域内上游面的壁面应力。

在无场力时，颗粒的重力通过颗粒之间以及颗粒与壁面之间的碰撞向壁面传递。当电场开始作用时，向上游面传递的部分颗粒重力被场力承担，使得上游面附近颗粒之间以及颗粒与壁面之间的相互作用被削弱。随着电场的增强，场力越来越强，直至完全地承担向上游面传递的颗粒重力，并最终将颗粒从上游面推离，形成空腔。当电场强度从160 MN/C增强到480 MN/C时，颗粒循环速率（R）的变化基本可以忽略（表 2），故而对空腔的形成无显著影响。由于颗粒流动的阻力也主要来自于颗粒之间以及颗粒与壁面之间的相互作用，因而在较强的电场下上游面附近颗粒流动的阻力较弱，流速明显较快。

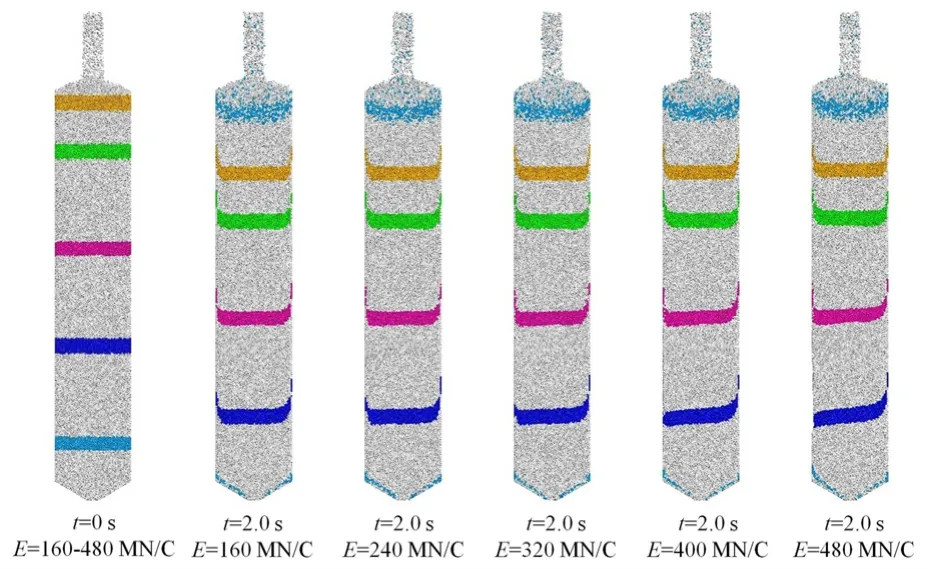
图2　细颗粒体系中，示踪颗粒在初始和电场作用下的分布Fig.2 Space distribution of trace particles in fine particle system under different field strength conditions at the onset of imposing the electric field and 2 s after onset

图3　细颗粒体系中电场强度对场力作用区域内上游面壁面应力的影响Fig.3 Effect of electric field intensity on normal stress of upstream wall in fine particle system

图4　细颗粒体系中电场强度对上游面附近颗粒流动的影响Fig.4 Effect of electric field intensity on flow behavior of particles near the upstream in fine particle system

表2　细颗粒体系中不同场强下的颗粒循环速率Table 2 Effect of electric field intensity on recycling rate in fine particle system

图4为细颗粒体系中，电场强度在空腔临界场强附近变化对上游面附近颗粒流动的影响。结果表明，上游面附近在电场强度为380 MN/C时，无空腔形成，而在电场强度为400 MN/C时有空腔形成。因此，对于本工作所用细颗粒体系，形成空腔的临界场强为400 MN/C。此外，场强在空腔临界场强附近变化也基本不影响颗粒的循环速率（表2）。

2.2混入粗颗粒体系中的空腔现象

向床层中混入粗颗粒以后，场强对上游面附近颗粒流动的影响如图5所示。结果显示，当粗颗粒的壁面摩擦系数（μcoarse）为 0.75时，若粗颗粒分散在床层中，见图 5（a），形成空腔的临界场强为440 MN/C；若其集中在壁面附近，见图5（b），这一临界场强减小到360 MN/C。当μcoarse从0.75减小到0.10时，这2种体系的空腔临界场强均增大，分别为500和550 MN/C。此外，上述4种体系中，当壁面摩擦系数为0.75的粗颗粒集中到壁面附近时，其空腔临界场强小于细颗粒体系的结果；其余3种体系的空腔临界场强都大于细颗粒体系下的结果。

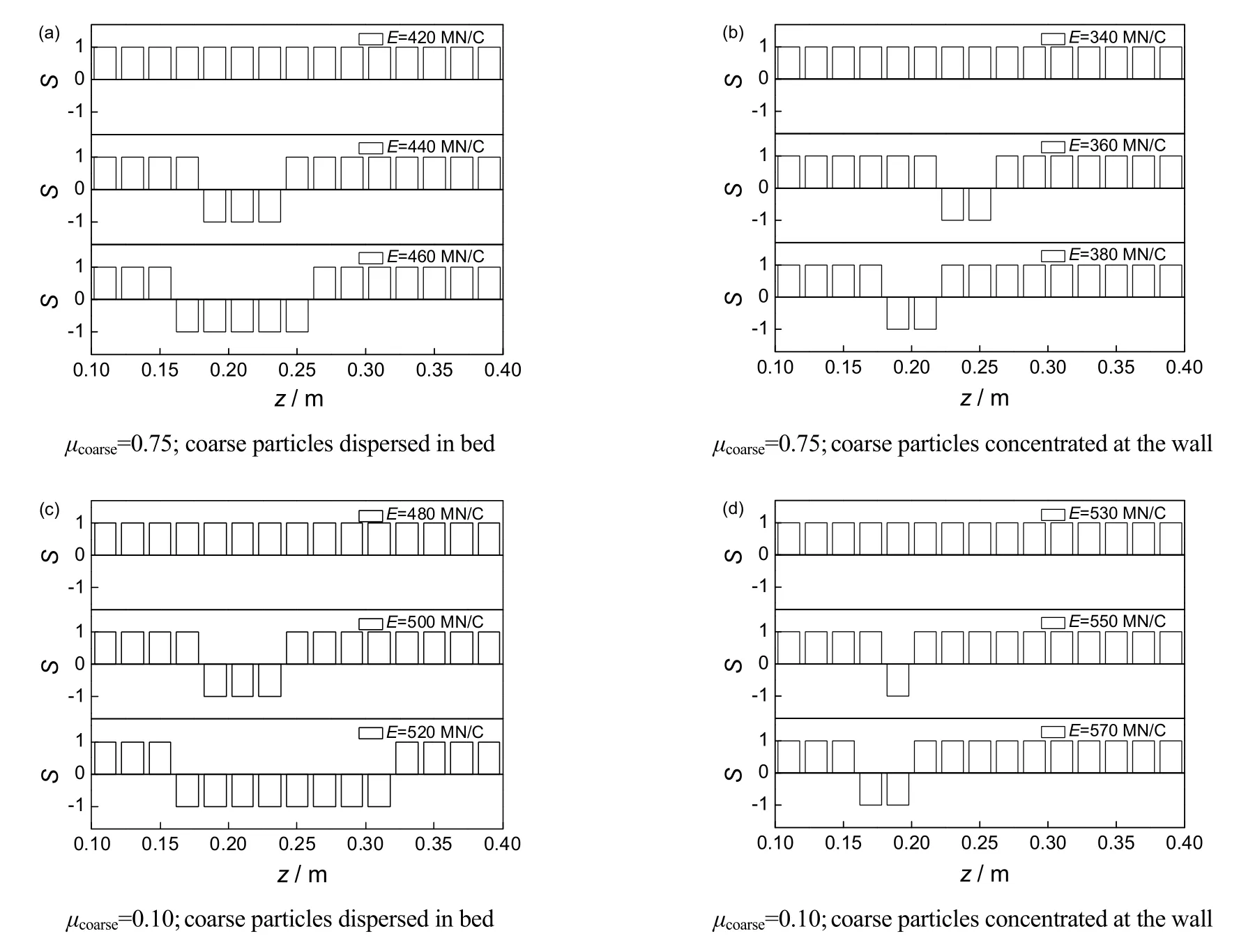
图5　混入粗颗粒体系中电场强度对上游面附近颗粒流动的影响Fig.5 Effect of electric field intensity on flow behavior of particles near upstream wall in systems composed of fine and coarse particles

在引入粗颗粒后，颗粒的循环速率如表3所示。将其与细颗粒体系的结果（表2）对比可以看到，向床层中混入粗颗粒使得颗粒循环速率有所下降。然而，其下降的程度较小，故不会影响壁面正应力［21］，即不影响向壁面传递的颗粒重力。因此，在混入粗颗粒后发生空腔的临界条件发生变化与颗粒循环速率的变化无关。此外，随着颗粒粒径的增大，颗粒所受到的场力以及颗粒本身的重力都增大，但两者的比值减小。因此，对于颗粒向上游面传递的重力来说，场力支撑作用的贡献随着颗粒粒径的增大而减小。故而，对于颗粒群向上游面传递的重力来说，场力支撑作用的贡献也随着粗颗粒的混入而减小，进而有利于增大形成空腔的临界场强。

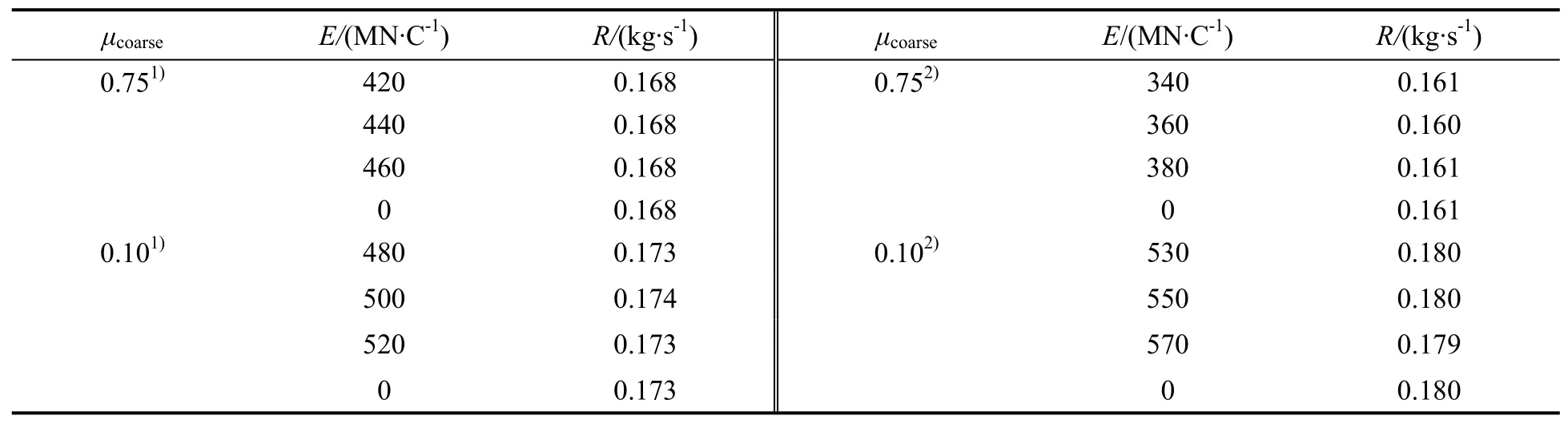
表3　混入粗颗粒体系中电场强度对颗粒循环速率的影响Table 3 Effect of electric field intensity on recycling rate in systems composed of fine and coarse particles

当粗颗粒与细颗粒的壁面摩擦系数相同，均为0.75时，将分散在床层中的粗颗粒集中到壁面附近使得无电场作用下的壁面应力减小（图 6）。这说明向壁面传递的颗粒重力减少。因此，形成空腔时，场力需要承担的颗粒重力减小，场强也相应减小。故在壁面摩擦系数为0.75的粗颗粒集中到壁面附近时，该体系空腔临界场强小于细颗粒体系的结果。

上述变化中向壁面传递的颗粒重力的减少，是由颗粒间碰撞的稳定性增强进而使得床层变得疏松引起的。在壁面附近，由于颗粒与壁面之间的摩擦系数较大，越靠近壁面的颗粒流动越慢［22］，颗粒之间由于这种流速的差异而不断发生碰撞，这种碰撞发生于等粒径和非等粒径的颗粒之间。其中，若碰撞是因为粗颗粒慢于细颗粒而形成的，其稳定性最强［23］，反之，则最弱［24］。当粗颗粒分散在床层中时，壁面附近同时存在粗颗粒慢于细颗粒和细颗粒慢于粗颗粒的情况。当分散在床层中的粗颗粒集中到壁面附近时，几乎所有的粗颗粒都慢于细颗粒。因此，壁面附近颗粒间的碰撞变得更稳定。这又进一步强化了远离壁面的区域内颗粒间的碰撞，使之也变得更稳定。因此，整个床层中颗粒之间的碰撞都变得更加稳定。

当粗颗粒分散在床层中时，若粗颗粒的壁面摩擦系数从 0.75减小到 0.10，无电场作用时的壁面应力增大（图 6）。这是由于分散在壁面上的粗颗粒与壁面之间的碰撞变得不稳定，进而使得床层变得致密并将更多的颗粒重力传递到壁面。因此，形成空腔的临界场强也增大。在粗颗粒分散在床层中时，仅有部分壁面被粗颗粒占据。当这些壁面摩擦系数较小的粗颗粒集中在壁面附近时，壁面几乎完全被粗颗粒所占据。这使得床层变的更加致密，并进一步增大向壁面传递的颗粒重力。故而，无电场作用时的壁面应力（图6）以及形成空腔的临界场强也增大。

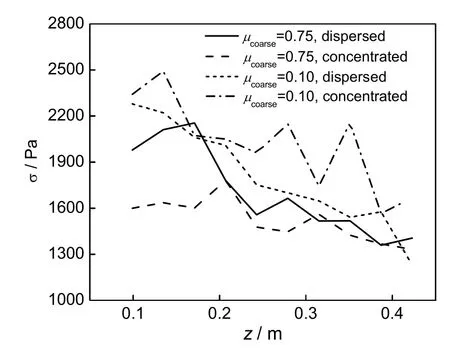
图6　混入粗颗粒的4种体系在无电场作用时的壁面应力分布Fig.6 Distribution of wall normal stresses in four systems composed of fine and coarse particles without electric field

3 结 论

采用DEM方法研究了向移动床中混入粗颗粒对空腔的抑制效应。粗颗粒的混入能够抑制空腔的形成。降低粗颗粒的壁面摩擦系数会进一步增大形成空腔的临界条件。随着粗颗粒在床层中分布情况的变化，形成空腔的临界条件也发生变化。若粗颗粒与细颗粒的壁面摩擦系数相同，将粗颗粒分散在床层中有利于抑制空腔的形成；若粗颗粒的壁面摩擦系数远小于细颗粒的壁面摩擦系数，将粗颗粒集中在壁面附近更有利于抑制空腔的形成。

随着向上游面传递的颗粒重力增大或是对其支撑作用中来自场力的贡献减小，空腔的形成都能够被抑制。对于向上游面传递的颗粒重力来说，粗颗粒的混入有利于削弱场力对其支撑作用的贡献，将壁面摩擦系数小的粗颗粒集中在壁面上或将壁面摩擦系数大的粗颗粒分散在床层中有利于使其增大。

符号说明

［1]杨 英， 彭 蓉， 肖立桢. 丙烷脱氢制丙烯及其经济性分析［J］. 石油化工技术与经济， 2014， 30（3）: 6-10. Yang Ying， Peng Rong， Xiao Lizhen. Economic analysison process of propane dehydrogenation to propylene［J］. Technology & Economy in Petrochemicals， 2014， 30（3）: 6-10.

［2]龙文宇， 徐 军， 范怡平， 等. 矩形移动床径向反应器内颗粒贴壁现象分析［J］. 化学反应工程与工艺， 2014， 30（1）: 15-21. Long Wenyu， Xu Jun， Fan Yiping， et al. Analysis on pinning in a rectangular moving beds with cross gas flow［J］. Chemical Reaction Engineering and Technology， 2014， 30（1）: 15-21.

［3]陈允华， 朱学栋， 吴勇强， 等. 移动床空腔现象及空腔尺寸［J］. 化工学报， 2006， 57（4）: 731-737. Chen Yunhua， Zhu Xuedong， Wu Yongqiang， et al. Phenomenon of cavity and its size in rectangular moving-bed［J］. Journal of Chemical Industry and Engineering， 2006， 57（4）: 731-737.

［4]Doyle III F J， Jackson R， Ginestra J C. The phenomenon of pinning in an annular moving bed reactor with crossflow of gas［J］. Chemical Engineering Science， 1986， 41（6）: 1485-1495.

［5]宋续祺， 金 涌， 龚美珊. 移动床径向反应器的催化剂颗粒层中应力分布和贴壁现象产生的条件［J］. 高校化学工程学报， 1993，7（4）: 352-361. Song Xuqi， Jin Yong， Gong Meishan. Profile of stress and phenomenon of pinning in an annular moving bed reactor with radial flow of gas［J］. Journal of Chemical Engineering of Chinese Universities， 1993， 7（4）: 352-361.

［6]宋续祺， 金 涌， 俞芷青， 等. 移动床径向反应器中气体离心流动对颗粒移动情况的影响［J］. 化工学报， 1993， 44（4）: 433-441. Song Xuqi， Jin Yong， Yu Zhiqing， et al. The formation of cavity in moving bed radial flow reactor［J］. Journal of Chemical Industry and Engineering， 1993， 44（4）: 433-441.

［7]王保平， 庞桂赐， 金 涌. 径向移动床反应器内贴壁现象的研究［J］. 石油学报， 1993， 9（3）: 78-87. Wang Baoping， Pang Guixi， Jin Yong. Study of pinning in a radial moving bed reactor［J］. Acta Petrolei Sinca， 1993， 9（3）: 78-87.

［8]陈允华， 朱学栋， 吴勇强， 等. 整流子对错流移动床颗粒行为的影响［J］. 过程工程学报， 2007， 7（4）: 639-645. Chen Yunhua， Zhu Xuedong， Wu Yongqiang， et al. Effects of internals on the particle behavior in a rectangular moving bed with gas cross-flow［J］. The Chinese of Process Engineering， 2007， 7（4）: 639-645.

［9]武锦涛， 陈纪忠， 阳永荣. 移动床中固体颗粒流动的实验研究和数值模拟［J］. 石油化工， 2004， 33（10）: 946-950. Wu Jingtao， Chen Jizhong， Yang Yongrong. Experiments and simulation for particles flow in the 2-D moving bed［J］. Petrochemical Technology， 2004， 33（10）: 964-950.

［10]Wu J， Binbo J， Chen J， et al. Multi-scale study of particle flow in silos［J］. Advanced Powder Technology， 2009， 20（1）: 62-73.

［11]Zhuh P， Zhou Z Y， Yang R Y， et al. Discrete particle simulation of particulate systems: a review of major applications and findings［J］. Chemical Engineering Science， 2008， 63（23）: 5728-5770.

［12]余莲英， 李艳洁， 徐 泳. 等粒径颗粒群流动特征实验研究［J］. 中国农业大学学报， 2006， 11（6）: 116-120. Yu Lianying， Li Yanjie， Xu Yong. Experimental study on flow characteristics of a stream of isodiametric sphere［J］. Journal of ChinaAgricultural University， 2006， 11（6）: 116-120.

［13]Majmudar T S， Behringer R P. Contact force measurements and stress-induced anisotropy in granular materials［J］. Nature， 2005， 435: 1079-1082.

［14]Cundall P A， Strack O D L. A discrete numerical model for granular assemblies［J］. Geotechnique， 1979， 29（1）: 47-65.

［15]Asmar B N， Langston P A， Matchett A J， et al. Validation tests on a distinct element model of vibrating cohesive particle systems［J］. Computers & Chemical Engineering， 2002， 26（6）: 785-802.

［16]Kruggel-Emdenh， Rickelt S， Wirtz S， et al. A numerical study on the sensitivity of the discrete element method forhopper discharge［J］. Journal of Pressure Vessel Technology， 2009， 131（3）: 031211-031220.

［17]Landryh， Laguë C， Roberge M. Discrete element representation of manure products［J］. Computers and Electronics in Agriculture， 2006，51（1/2）: 17-34.

［18]Masson S， Martinez J. Effect of particle mechanical properties on silo flow and stresses from distinct element simulations［J］. Powder Technology， 2000， 109（1/3）: 164-178.

［19]Wu C L， Ayeni O， Berrouk A S， et al. Parallel algorithms for CFD-DEM modeling of dense particulate flows［J］. Chemical Engineering Science， 2014， 118: 221-244.

［20]陈允华， 朱学栋， 吴勇强， 等. 移动床贴壁现象的研究［J］. 高校化学工程学报， 2007， 21（3）: 404-410. Chen Yunhua， Zhu Xuedong， Wu Yongqiang， et al. Investigation of pinning in moving bed［J］. Journal of Chemical Eningeering of Chinese Universities， 2007， 21（3）: 404-410.

［21]Couto A， Ruiz A，herráez L， et al. Measuring pressures in a slender cylindrical silo for storing maize. Filling， static state and discharge with different material flow rates and comparison with Eurocode 1 part 4［J］. Computers and Electronics in Agriculture， 2013， 96: 40-56.

［22]Yang S C，hsiau S S. The simulation and experimental study of granular materials discharged from a silo with the placement of inserts［J］. Powder Technology， 2001， 120（3）: 244-255.

［23]Golick L A， Daniels K E. Mixing and segregation rates in sheared granular materials［J］. Physical Review E， 2009， 80（4）: 042301.

［24]Ueda T， Matsushima T， Yamada Y. Effect of particle size ratio and volume fraction on shear strength of binary granular mixture［J］. Granular Matter， 2011， 13（6）: 731-742.

Inhibiting Cavity Formation by Mixing Coarse Particles into a Moving Bed

Xu Pengkai， Duan Xuezhi， Qian Gang， Zhou Xinggui
State Key Laboratory of Chemical Engineering， East China University of Science and Technology， Sanghai 200237， China

Inhibiting cavity formation by mixing coarse particles into a moving bed was investigated by the discrete element method. The results indicated that coarse particles contributed to inhibiting the cavity formation in a moving bed， especially when the wall friction coefficients of coarse particles were lower than those of fine particles. To enhance the effect of coarse particles on cavity formation in the moving bed， the coarse particles should be dispersed in the bed when the wall friction coefficients of coarse particles were the same as those of fine particles， but should be concentrated at wall when the wall friction coefficients of coarse particles were significantly smaller than those of fine particles.

cavity； particle size； load transmission； space distribution； wall friction coefficient； discrete element method

TQ018

A

1001—7631 （ 2015 ） 04—0289—08

2015-02-06；

2015-04-12。

许鹏凯（1985—），男，博士研究生；周兴贵（1966—），男，教授，通讯联系人。E-mail: xgzhou@ecust.edu.cn。

国家重大基础研究计划973计划（2012CB720501）。