Pd/α-Al2O3催化乙炔选择性加氢微观反应动力学

王新宇，隋志军，朱贻安，周兴贵

Pd/α-Al2O3催化乙炔选择性加氢微观反应动力学

王新宇，隋志军，朱贻安，周兴贵

华东理工大学化学工程联合国家重点实验室，上海 200237

采用乙炔顺序加氢的反应机理，利用已报道的密度泛函理论（DFT）计算结果进行了乙炔加氢反应的微观反应动力学模拟，所得的乙炔加氢反应动力学具有共同的特征。利用实验获得的Pd/α-Al2O3催化乙炔加氢反应动力学数据，对上述DFT数据进行校验，发现经过不超过0.1 eV的调整，微观反应动力学模拟结果与实验结果符合很好，说明DFT数据是良好的微观反应动力学参数来源。利用优化后的动力学参数模拟了工业生产范围内的动力学，获得了速率控制步骤和表面物种等信息，可为双曲动力学模型的建立提供参考。

乙炔加氢 氧化铝负载钯催化剂 微观反应动学

乙炔加氢是乙烯工业中的一个重要反应。从烃类裂解得到的乙烯中含有少量的乙炔杂质，它的存在会影响后续乙烯聚合工艺的效果，高浓度的乙炔甚至会导致聚合催化剂中毒［1］。通常利用选择性加氢反应使乙炔转化为乙烯，将乙烯产品中乙炔的浓度降为10-6量级［2］，同时要求降低乙炔生成乙烷的选择性，以避免物料损失和反应器飞温，这些都要依靠准确且可靠的动力学模型。乙炔加氢反应体系看似十分简单，但建立适用范围广且精度高的动力学模型存在很大难度：一是反应中乙炔体积分数从1%的量级降低至 10-6的量级，这要求动力学模型的适用浓度范围非常广，采用传统动力学方法时，意味着巨大的实验工作量；二是乙炔加氢反应器出口乙炔浓度必须达到10-6的量级，对动力学实验的精度也是巨大挑战。这种情况下，采用微观反应动力学方法就十分有必要。

微观反应动力学方法主要利用理论模拟以及表面科学实验等结果确定各基元反应的动力学参数，建立微观反应动力学模型。由于在建立过程中不需要进行速率控制步骤等假设，因此可以在较广的实验范围内描述动力学，所获基元步骤动力学参数还可以拓展至其他反应体系［3］。随着分子模拟和计算机技术的进步，密度泛函理论（DFT）计算在催化研究中的作用越来越受到重视［4］。大量DFT计算结果为微观反应动力学模型的建立提供了很好的参数来源［5］，而系统的微观反应动力学分析将有助于充分发掘DFT模拟结果的动力学意义。关于乙炔加氢反应的DFT研究较多，但将理论计算与实验研究相结合的较少。本工作将利用不同研究者获得的 DFT计算结果建立微观反应动力学模型，与实验室获得的动力学数据进行比较，以校验基元步骤动力学参数，并通过模拟获得工业乙炔加氢工艺条件范围内双曲型动力学模型建立所需的信息。

1 实验部分

1.1 催化剂制备

Pd/α-Al2O3催化剂采用等量浸渍法制备。以H2PdCl4为前驱体溶液，按质量分数为1%的负载量浸渍后，室温下老化12h，于120 ℃烘干12h，最后在马弗炉于300 ℃下焙烧2h，然后升温至550 ℃焙烧3h。催化剂使用前在反应器中原位还原，还原条件为150 ℃下通入H2和Ar混合气（H2体积分数为10%）还原2h。

1.2 催化剂表征

比表面（BET）测试在Micromeritics公司的ASAP2010型物理吸附仪上进行，测量前样品在190 ℃，0.133 kPa真空状态下脱气6h，之后在77 K下进行N2吸附；样品晶相结构用D/max2550V型X射线衍射（XRD）仪测定，测试条件为Cu靶，电压40 kV，电流100 mA；化学吸附在Micromeritics公司的AutoChemⅡ2920型化学吸附仪上进行，催化剂在氦气气氛中升温至120 ℃，保持恒温干燥1h，10 ℃/min 升温至150 ℃，通入H2和Ar混合气（H2体积分数为10%）还原2h，之后通入氦气并升温至180 ℃，保持恒温并吹扫30 min，降至室温后进行脉冲吸附测试，吸附气体为一氧化碳；透射电镜（TEM）的表征在JOEL公司的JEM2010上进行，操作电压为200 kV。

1.3 动力学实验

反应装置为Altamira公司的Microactivity全自动控制小型催化反应器。反应器为内径8 mm的不锈钢管，反应系统置于带有温度控制的热箱中。反应器温度控制精度为0.1 ℃，压力控制精度10 kPa，流量控制精度0.1 mL/min。乙炔加氢的动力学实验在达到稳态的催化剂样品上进行，即新鲜催化剂在设定反应条件下反应12h，使催化剂活性达到基本不变（3h内乙炔转化率变化小于1%），即认为催化剂达到稳态。

反应前后的气体浓度采用在线四通道Inficon 3000微型气相色谱测定，通道A，B，C和D分别安装分子筛、分子筛、Plot U和氧化铝色谱柱。其中通道A用于测定氢气和氮气的浓度，通道B测定碳四组分，通道C测定乙炔浓度，通道D测定乙烯及乙烷的浓度，分析可在2 min内完成。每个样本点取样5次，取平均值作为实验数据。

在动力学实验前，进行了空白实验和排除内外扩散影响的实验。空白实验中，不锈钢反应器中装填有0.4 g的石英砂，在100 ℃条件下乙炔和氢气的转化率均小于0.1%，说明稀释剂石英砂及反应器管壁对动力学实验的影响可以排除。采用了具有4种不同颗粒直径的催化剂进行内扩散影响的研究。实验在80 ℃，气体总流量为290 mL/min，催化剂质量0.05 g条件下进行，结果表明，当催化剂粒径小于0.2 mm时，内扩散影响可以排除，本工作采用颗粒粒径小于0.15 mm的催化剂进行实验。外扩散影响的实验中，催化剂装填量为0.05～0.10 g，改变进料气体流速并测试乙炔转化率。实验结果表明，当气体总流速大于245 mL/min时，乙炔转化率与通过催化剂床层的反应气流线速度无关，外扩散的影响可以忽略，本工作采用的反应气体流速为290 mL/min。

采用微观反应动力学方法建立动力学模型，无需大量数据进行动力学参数的经验回归，动力学实验数据的作用是校验模型参数，动力学实验条件可采用24析因实验设计。根据以上预实验反应结果，参考工业碳二加氢反应器的操作条件，选定4个因素和实验范围：反应温度为80和75 ℃；乙炔含量为0.9%和0.6%（体积分数）；氢炔比1.8和1.5；乙烯含量为80%和70%（体积分数）。其他实验条件为催化剂质量0.05 g，反应压力2.1 MPa。实验条件和动力学实验结果如表1所示。

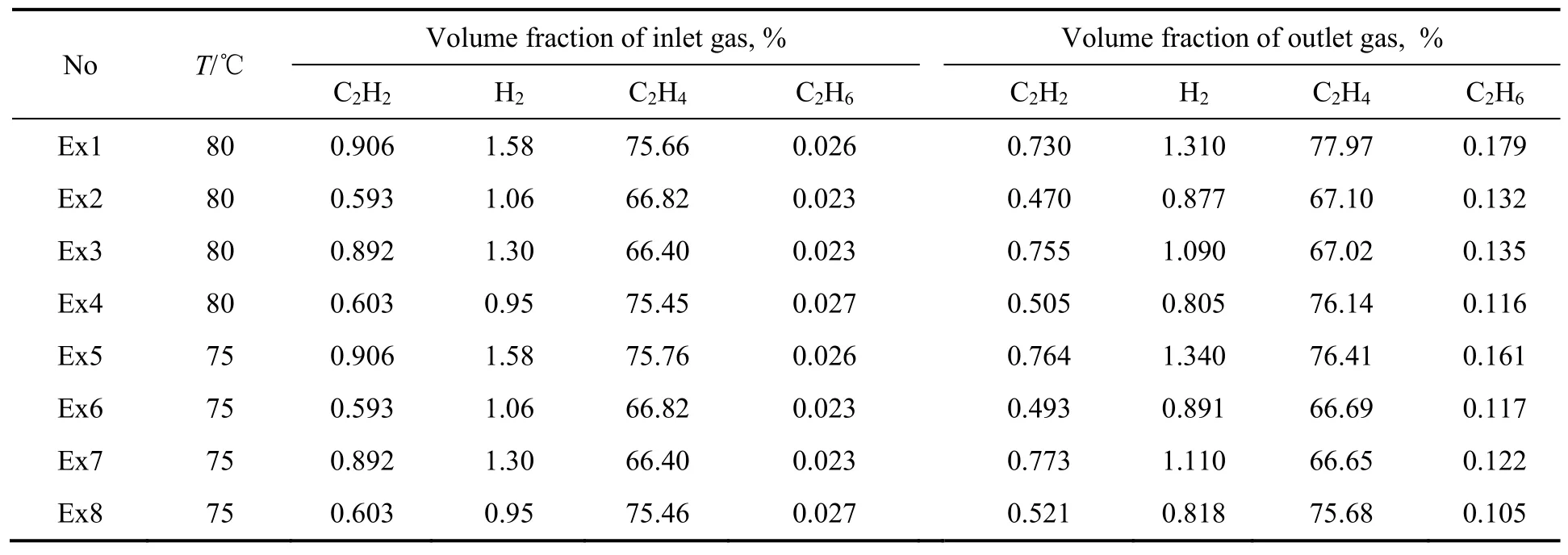
表1　动力学实验条件与结果Table 1 Kinetic experimental conditions and results

2 微观反应动力学模型

乙炔加氢反应机理的研究很多［6］，一般认为，在 Pd（111）晶面上加氢遵循顺序加氢反应机理，根据反应机理可以直接写出各基元步骤及其速率方程，如表2所示。

表2　基元反应与反应速率Table 2 Elementary reaction steps and reaction rate expressions

表中：ri为不同基元步骤的反应速率；ki和k-i为各基元步骤的正逆步骤的速率常数；Pj表示气体物种的分压；θj代表不同物种的表面覆盖度，下标j表示不同的反应物种；θ表示未被覆盖空白位点的百分比；*表示空白吸附位。各物种表面覆盖度的和满足归一性，即：

基元步骤的速率常数可以表示为：

式中：A为指前因子，s-1；Ea为反应活化能，J/mol；R为常数8.314，J/（mol·K）；T为绝对温度，K。假定动力学实验反应器满足平推流反应器假设，根据物料衡算式可以列出反应器模型如下：

气相物种：

表面物种：

式中：F为气体摩尔流率，mol/s；m为催化剂质量，g；R表示每克催化剂气体反应速率，mol/ s；Gsite是每克催化剂的活性位点数，mol。

3 结果与讨论

3.1 催化剂结构

物理吸附测得的载体的比表面积为13.96 m2/g，载体的总孔容为0.046 cm3/g，平均孔径为12.2nm。载体XRD图的衍射峰的角度及峰强度都与α-Al2O3的标准卡片（PDF#88-0826）相符，可以判断载体为α-Al2O3。一氧化碳化学吸附测得达到稳态催化剂的分散度为40%，测得催化剂粒径为2.8nm；由TEM照片统计的粒径分布如图1所示，计算得到平均粒径为2.87nm。可见两种方法测定的粒径是一致的。由Pd分散度的测定结果和Pd的负载量，可以计算表面Pd原子的数量为每克催化剂3.76×10-5mol，在催化剂粒径较大时，表面Pd被认为以Pd（111）晶面为主［7］， 而乙炔加氢的主要活性位点为Pd（111）晶面，因此认为Pd表面原子数量等于活性位点数Gsite，该值被用于后续的微观反应动力学模拟。

图1　催化剂TEM照片及Pd粒径分布Fig.1 The TEM image of catalyst and the propotion of Pd diameter

3.2 基元步骤动力学参数的确定

本工作所采用的各基元步骤活化能的数据主要来源于Studt等［8-11］对Pd（111）晶面的DFT计算结果。在使用前，首先进行热力学一致性校验。校验采用拉格朗日乘子法，将 DFT计算得到的总反应焓变与实际总包反应焓变的差值按比例分配到每个基元反应的活化能中。拉格朗日乘子法采用的目标函数及约束条件如下：

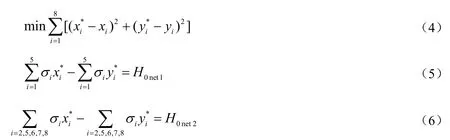
式中：xi和yi分别代表校验之前正逆反应的活化能；xi*和yi*分别代表校验之后正逆反应的活化能；下标i表示基元步骤序号；σi代表反应路径中基元步骤的化学计量系数；乙炔加氢生成乙烯和乙烯加氢生成乙烷的反应热数值分别是H0 net 1为- 176 kJ/mol和H0 net 2为-136 kJ/mol［12］。校验前后的活化能数据列于表3中。

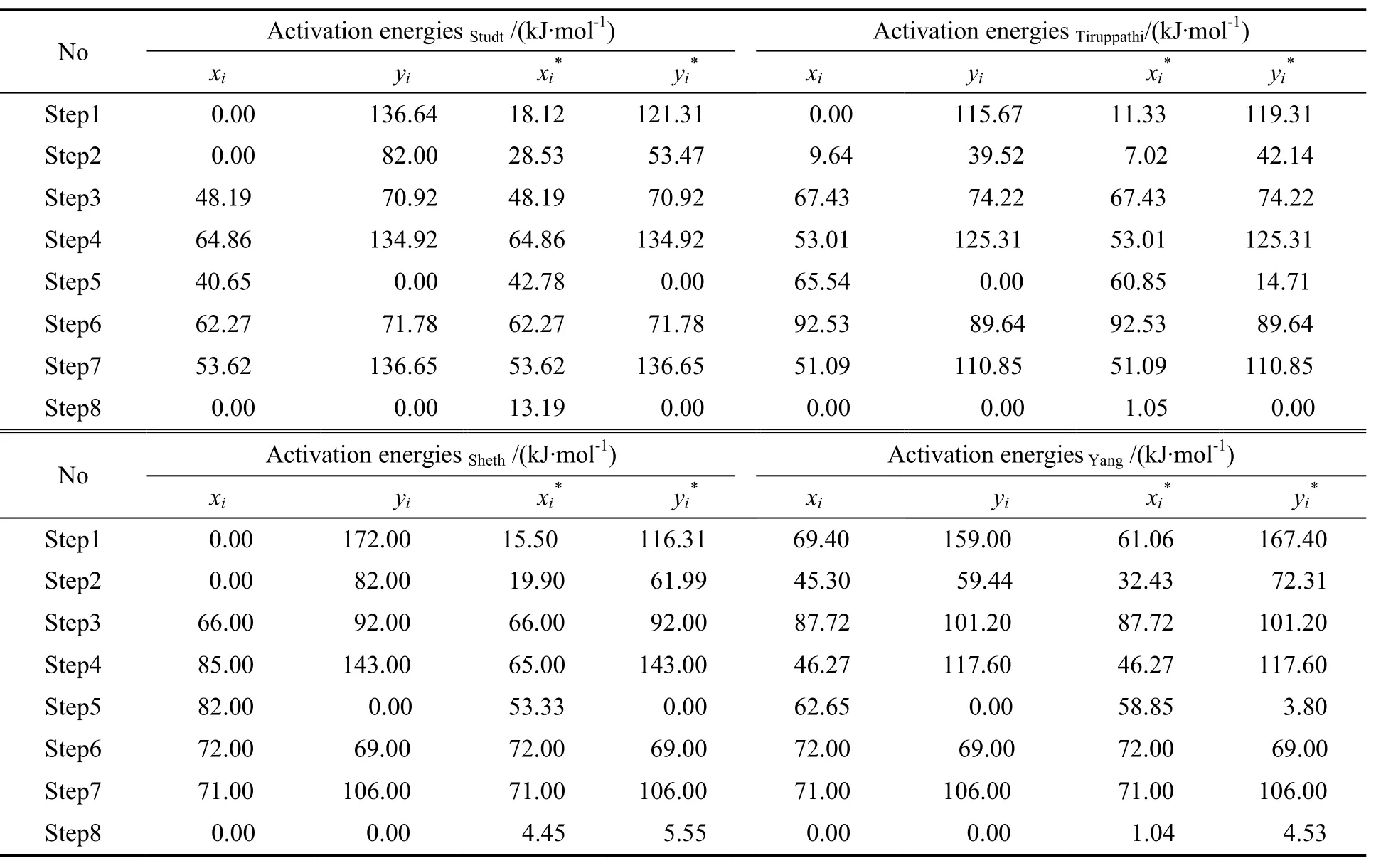
表3　热力学一致性校验前后的基元步骤活化能Table 3 Activation energies of elementary steps before and after thermodynamic consistency correction

吸脱附步骤的指前因子数据来源于文献［13-15］，表面基元反应的指前因子采用多米西克［3］用过渡态理论的估计值。各基元步骤指前因子如表4所示，Afor和Arev分别代表正反应和逆反应的指前因子。

表4　乙炔加氢基元步骤指前因子Table 4 The pre-exponential factor of elementary steps

3.3 不同来源DFT数据动力学模拟结果比较

首先根据表3和表4确定的基元步骤参数对乙炔加氢进行微观反应动力学模拟，以检验不同来源DFT数据的差别。模拟采用的基准反应的初始条件为温度353.15 K，进口气体的初始组成乙炔0.9%，氢气1.6%，乙烯80%和乙烷0.025%，总压为2.1 MPa。为得到反应级数及反应活化能等信息，采用单因素考察实验，模拟所得乙炔反应级数、氢气反应级数及反应活化能如图2所示。

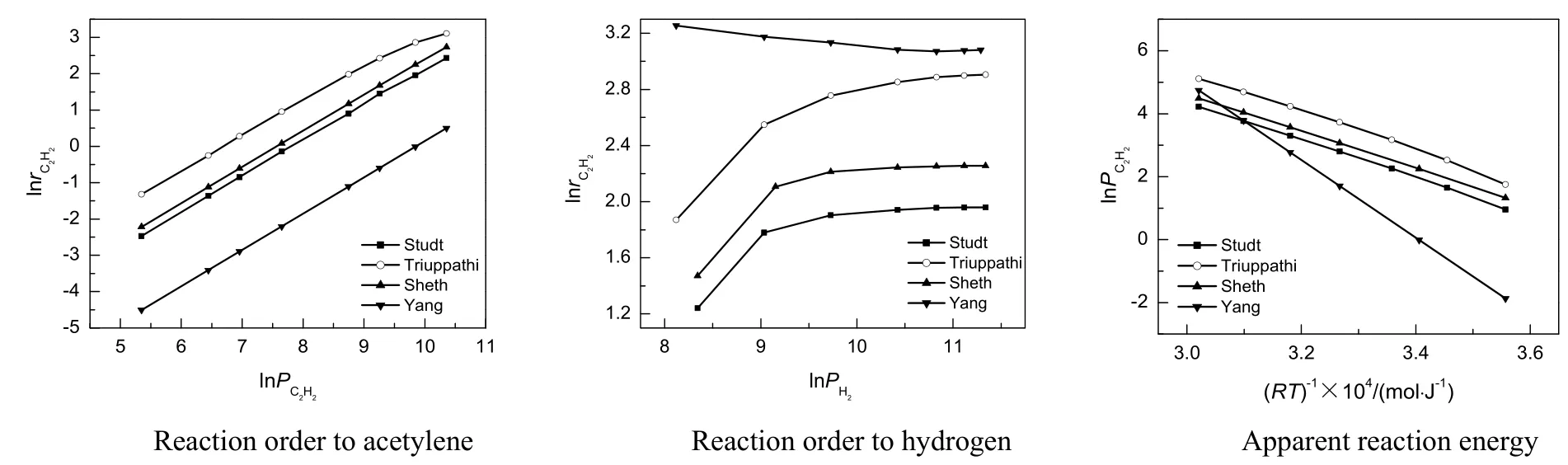
图2　不同来源DFT数据微观反应动力学模拟结果比较Fig.2 The comparison of microkinetic modeling results based on different DFT data

由图2的模拟结果可得出，不同来源的DFT计算获得的基元步骤活化能有很大不同，但模拟所得的动力学特征存在很多共性，如模拟得到的对乙炔的反应级数都是1级，这与Men'shchikov等［16，17］的研究结果相符合；加氢反应对氢气的反应级数在较高的氢炔比时（氢炔比大于等于1.5）为0级，而当氢气浓度较低时，氢气的反应级数会随着氢气浓度的下降而升高，这与Bos等［18］的报道结果相符。根据微观动力学模拟，还可以得出催化剂表面物种覆盖率和反应速率控制步骤等微观信息，在4组模拟结果中，都是以乙烯基加氢生成乙烯（Step4）作为整个反应的速率控制步骤，乙烯（C2H4*）为表面最丰物种，乙烯基（C2H3*）为表面次丰物种。因此可以认为，由4组DFT数据模拟得到的动力学参数都能够很好地反应乙炔加氢反应的特点，可以用作乙炔加氢反应的动力学参数。

模拟结果也有一定的差异。通过模拟得到的乙炔加氢反应活化能Studt为62.51 kJ/mol，Tiruppathi为67.89 kJ/mol，Sheth为58.91 kJ/mol和Yang为122.36 kJ/mol。文献报道的反应活化能一般在10～150 kJ/mol浮动［6，16-18］，主要受到催化剂粒径、载体、次表面积氢和积炭的影响，因此模拟的活化能结果位于文献报道值的范围内。值得提出的是，这里采用的Yang等［11］的DFT数据是在积炭Pd（111）表面获得结果，这可能是导致模拟所得反应活化能较高的主要原因。最后，根据模拟得到的反应结果和实验得到的反应结果，分别计算了4组模拟结果与实验值的残差，发现以Studt等报道的DFT数据模拟所得的结果与实验值残差平方和最小（5.84×10-4），与实验值差距不大。因此，采用Studt等计算的DFT数据作为进一步动力学模拟的参数。

3.4 动力学参数优化

为了获得实际Pd催化剂上的动力学参数，根据动力学实验结果采用最小二乘法对Studt等报道的DFT数据进行优化调整，优化采用的算法为Levenberg-Marquardt算法。优化得到的动力学参数如表5所示，实验数据与模拟结果的比较如图3所示。从拟合结果可看到，在9.62 kJ/mol 即0.1 eV以内调整基元步骤活化能数值，即可使模拟得到的结果与实验值吻合良好，这也说明尽管DFT计算与实验之间存在表面和压力等差异，但仍可以较好地应用到实际乙炔加氢反应中。比较模拟得到的结果与实验值可以看到，反应出口浓度中，乙炔、乙烯与氢气的拟合效果较好，相对而言模拟所得的乙烷浓度与实际值存在一定的误差，但在可接受范围内。

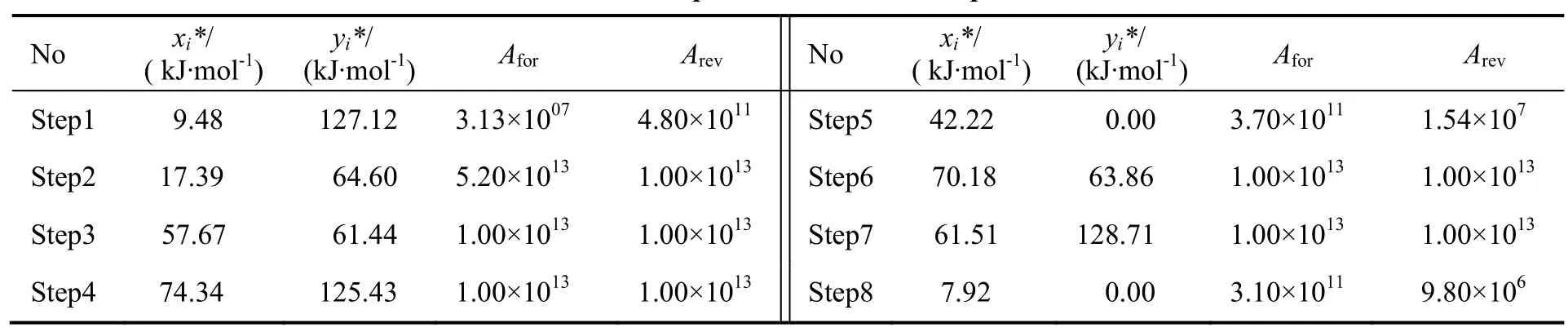
表5　优化后微观反应动力学参数Table 5 The optimized microkinetic parameters

3.5 微观反应动力学模拟结果

微观反应动力学方法的缺点是没有简单明确的动力学方程，应用于反应器设计和优化时不方便使用。而常用的双曲型动力学方程的推导需要进行一定的假设，如反应速率控制步骤和表面最丰物种等以简化模型。可以将两种动力学方法结合，采用微观反应动力学模拟检验速率控制步骤，确定表面物种覆盖率等，在此基础上建立的双曲动力学模拟，使其理论基础更加牢固。根据以上获得的优化后基元步骤动力学参数，对适用于工业应用范围内的反应条件进行了模拟，得到了不同条件下的速率控制步骤和表面最丰物种的信息，模拟结果如表6所示。由表中数据可以发现，在模拟反应条件范围内催化剂表面最丰物种及反应速率控制步骤都没有变化，与参数未经调整前的结果也一致，可以在此基础上建立双曲动力学模型。另外，在以上模拟范围，模拟所得乙炔加氢反应活化能约为60～62 kJ/mol，对氢气的反应级数接近0级，对乙炔的级数接近1级。这些数据可供其他研究者参考。

图3　乙炔加氢反应后气相组分含量与模拟值比较Fig.3 Comparison of experimental and simulated gas content in outlet

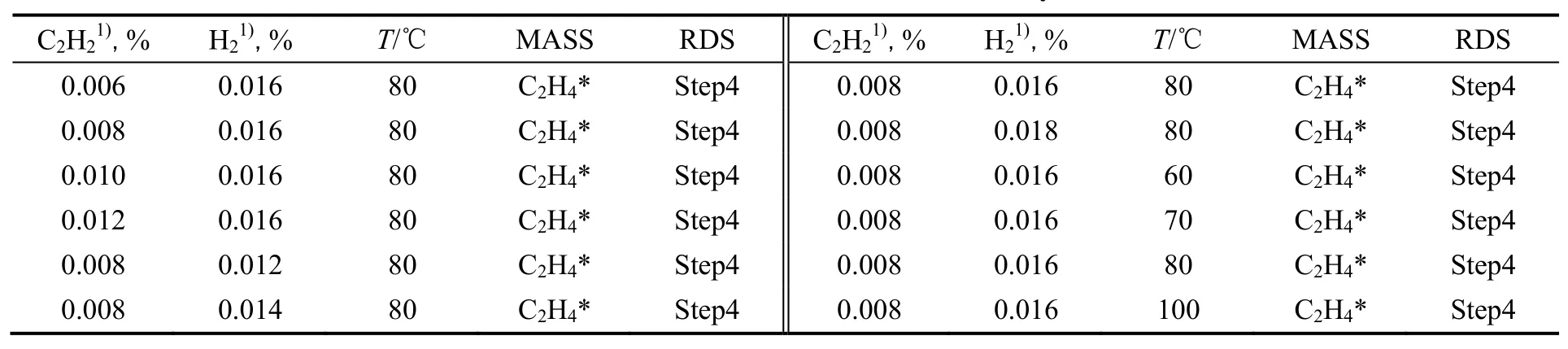
表6　微观动力学模拟结果Table 6 The results of microkinetic analysis

4 结 论

a）利用不同来源的DFT数据进行模拟，结果得到相似的乙炔加氢反应的动力学特性，加氢反应对乙炔的反应级数为1级，在高氢气浓度下对氢气的反应级数为0级，随着氢气浓度的降低反应级数逐渐升高，乙烯基加氢生成乙烯步骤是总反应的速率控制步骤。

b）根据动力学实验结果，将Studt等报道的DFT数据在0.1eV范围内进行调整，即可使微观反应动力学模拟与实验值吻合良好，说明DFT计算结果可用于实际反应的微观反应动力学模拟。

c）应用优化后的动力学参数，对工业适用条件范围内的动力学特性进行了模拟，得到不同条件下速率控制步骤、反应级数及活化能等信息，可为双曲型动力学模型的建立提供参考。

［1]戴 伟， 朱 警. C2 馏份选择加氢工艺和催化剂研究进展［J］. 石油化工， 2000， 29（7）: 535-540.Dai Wei， Zhu Jing. Advances in process and catalysts for selectivehydrogenation of acetylene［J］. Petrochemical Technology， 200， 29（7）: 535-540.

［2]李立新. 乙炔前加氢反应器运行稳定性的研究［J］. 化学反应工程与工艺， 2004， 20（1）: 47-52. Li Lixin. Analysis on the stability of the front-end acetylenehydrogenation reactor［J］. Chemical Reaction Engineering and Technology，2004， 20（1）: 47-52.

［3]多米西克. 多相催化微观动力学［M］. 沈俭一， 译. 北京: 国防工业出版社， 1998: 158-161.

［4]朱贻安， 周兴贵， 袁渭康. 多相催化微观动力学与催化剂理性设计［J］. 化学反应工程与工艺， 2014， 30（3）: 205-211. Zhu Yi’an， Zhou Xinggui， Yuan Weikang. Microkinetics ofheterogeneous catalysis and rational catalyst design［J］. Chemical Reaction Engineering and Technology， 2014， 30（3）: 205-211.

［5]李 庆， 杨明磊， 隋志军， 等. 基于密度泛函理论计算的丙烷脱氢动力学［J］. 化学反应工程与工艺， 2012 （2）: 97-103. Li Qing， Yang Minglei， Sui Zhijun， et al. Kinetics of propane dehydrogenation based on density functional theory［J］. Chemical Reaction Engineering and Technology， 2012 （2）: 97-103.

［6]Borodziński A， Bond G C. Selectivehydrogenation of ethylene in ethane-rich streams on palladium catalysts， part 2: steady-state kinetics and effects of palladium particle size， carbon monoxide， and promoters［J］. Catalysis Reviews， 2008， 50（3）: 388-401.

［7]Crespo-Quesada M， Yarulin A， Jin M， et al. Structure sensitivity of alkynolhydrogenation on shape-and size-controlled palladium nanocrystals: which sites are most active and selective？［J］. Journal of the American Chemical Society， 2011， 133（32）: 12787-12794.

［8]Studt F， Abild-Pedersen F， Bligaard T， et al. Identification of non-precious metal alloy catalysts for selectivehydrogenation of acetylene［J］. Science， 2008， 320（5881）， 1320-1322.

［9]Tiruppathi P， Low J J， Chan A S Y， et al. Density functional theory study of the effect of subsurfaceh， C， and Ag on C2H2hydrogenation on Pd （111）［J］. Catalysis Today， 2011， 165（1）: 106-111.

［10]Sheth P A， Neurock M， Smith C M. A first-principles analysis of acetylenehydrogenation over Pd（111）［J］. The Journal of Physical Chemistry B， 2003， 107（9）: 2009-2017.

［11]Yang B， Burch R，hardacre C， et al. Influence of surface structures， subsurface carbon andhydrogen， and surface alloying on the activity and selectivity of acetylenehydrogenation on Pd surfaces: a density functional theory study［J］. Journal of Catalysis， 2013， 305: 264-276.

［12]李梦龙. 化学数据速查手册［M］. 北京: 化学工业出版社， 2003: 56-59.

［13]Sellersh， Gislason J. Adsorption and desorption rate constants for small molecules on metal surfaces: an example of Trouton'srule［J］. Surface Science， 1999， 426（2）: 147-153.

［14]Mitsui T， Rose M K， Fomin E， et al.hydrogen adsorption and diffusion on Pd （111）［J］. Surface Science， 2003， 540（1）: 5-11.

［15]Sellersh. Entropies of desorption from temperature programmed desorption data: trends and applications to rate constant determinations［J］. The Journal of Physical Chemistry B， 2003， 107（37）: 10206-10208.

［16]Men'shchikov V A， Fal'kovich Y G， Aerov M E.hydrogenation kinetics of acetylene on a palladium catalyst in the presence of ethylene［J］. Kinet Catal， 1975， 16（6）: 1335-1338.

［17]Vincent M J， Gonzalez R D. A Langmuir-Hinshelwood model for ahydrogen transfer mechanism in the selectivehydrogenation of acetylene over a Pd/γ-Al2O3catalyst prepared by the sol-gel method［J］. Applied Catalysis A: General， 2001， 217（1/2）: 143-156.

［18]Bos A N R， Botsma E S， Foeth F， et al. A kinetic study of thehydrogenation of ethylene and ethane on a commercial Pd/Al2O3catalyst［J］. Chemical Engineering and Processing: Process Intensification， 1993， 32（1）: 53-63.

Microkinetics of Acetylene Selectivehydrogenation over Pd/α-Al2O3Catalyst

Wang Xinyu， Sui Zhijun， Zhu Yian， Zhou Xinggui
State Key Laboratory of Chemical Engineering， East China University of Science and Technology， Shanghai 200237， China

The microkinetic modeling ofhydrogenation of acetylene following a sequentialhydrogenation mechanism was carried out based on density functional theory（DFT） results from other researchers. All the modeling results showed that the kinetic behavior of acetylenehydrogenationhad some common characteristics. The kinetic parameters from the DFT results were adjusted according to the kinetic data obtained from the experiments over the Pd/α-Al2O3catalyst. It was found that the microkinetic modeling results fitted well to the experimental results after adjustment within 0.1 eV， which indicated that DFT results could be a good resource for practical reaction kinetic modeling. Some key information for macrokinetic model building， rate determine steps and surface coverage were obtained from the microkinetic modeling using the optimized parameters under the industrial operation conditions.

acetylenehydrogenation； palladium loaded alumina catalyst； microkinetic modeling

TQ032

A

1001—7631 （ 2015 ） 04—0322—08

2015-01-13；

2015-05-25。

王新宇（1989—），男，硕士研究生；隋志军（1974—），男，副教授，通讯联系人。E-mail: zhjsui@ecust.edu.cn。

973计划项目（2012CB720500）；国家自然科学基金项目（21376076）。