基于错位样本的电力系统负荷预测
2015-09-13王惠中王岳锋
王惠中,刘 轲,王岳锋
(1.兰州理工大学 电气工程与信息工程学院,兰州 730050;2.甘肃省工业过程先进控制重点实验室,兰州 730050;3.国网浙江诸暨市供电公司,诸暨 311800)
0 引言
智能电网的建设以及市场化的进一步加深不仅对电网的安全稳定运行要求更高,还对短期电力负荷预测的速度和精度提出了更高的要求[1]。不断改进负荷预测方法,提高预测速度和精度,对市场主体都有重要意义。对于电力生产,短期负荷预测是电力企业制定发电计划和电网供需平衡的关键;对于电力市场化,随着电力的经营方式从垄断变为市场竞争,短期负荷预测的作用日益重要,它成为了电厂报价的根据,更是保证电网安全稳定运行的重要前提,其预测精度直接影响到电力企业的经济效益。总的来说,通过精确的短期电力负荷预测能够确保电网安全、稳定、优质、经济的运行[2]。
传统的负荷预测方法都是在算法上进行改进,忽略了影响因素的重要性。本文结合国内外学者对短期负荷预测的研究成果,充分考虑气温的积累效应提出了错位样本概念并考虑尽可能多的样本。通过样本选择,选取合适的样本进行负荷预测。最后根据我国南方某市的真实负荷数据和天气数据,采用最小二乘支持向量机(LSSVM)模型进行负荷预测。
1 影响负荷因素分析
影响电力负荷的因素主要是自然和社会因素。本文尽可能多的收集历史负荷资料和历史天气资料,将这些数据分类整理后进行相关性分析和对比,从中选出对负荷影响最大的因素。综合分析各种因素,可以将这些因素可分为以下两个类型:日期因素和气象因素。
1.1 气象因素
气象因素,它对负荷的影响最大,夏季的空调负荷会导致一个夏季峰值负荷,冬季的取暖负荷也会使负荷急剧增加。其他天气情况也间接或直接对负荷造成影响,例如降雨会直接影响到农业负荷,湿度与温度的共同作用会加剧电力负荷变化等[5]。因此,近年来考虑多个气象因素产生的耦合效果的综合气象因素应运而生,这些因素并不是单独作用的,它们往往会协同起来共同影响电力负荷。本文主要考虑的综合气象因素包括实感温度,温湿指数及人体舒适度等。参考公式如下。
1)实感温度Te:亦称有效温度。在静止饱和的大气条件下使人感到的温度[6]。其计算公式为:
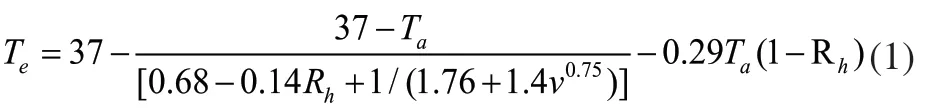
式中,Te为实感温度,℃;Ta为温度,℃;Rh为相对湿度,%;v为风速,m/s。
2)温湿指数THI:表示人们对环境温度和湿度感到舒适的程度[7]。其计算公式为:
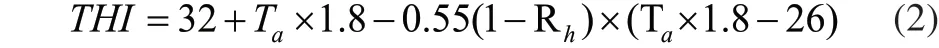
式中,THI为温湿指数;Ta为温度,℃;Rh为相对湿度,%。
3)人体舒适度SD:指湿度、温度、风速对人体的综合作用,既人体在大气环境中舒适程度[8]。其计算公式为:
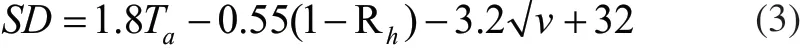
式中,SD为人体舒适度指数;Ta为温度,℃; Rh为相对湿度,%;v为风速,m/s。
4)寒湿指数CHI:在冬季衡量寒冷程度时,除了考虑气温、风速两种指标,还应考虑湿度作用[9]。计算公式为:
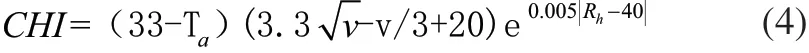
式中CHI为寒湿指数;Ta为气温;v为风速;Rh为相对湿度。
本文考虑的单一气象因素主要是:气温、相对湿度、降水量和风速等。由于地区气候季节性差异所以各种气象因素并不一定都适合成为预测地的负荷预测训练样本。为了选取合适的训练样本,采用相关系数对上述单一气象因素和综合气象因素进行相关性分析,从而选出最有利于负荷预测的气象因素。公式如下:

X,Y为二元随机变量,ρ是度量变量X和Y之间线性相关密切程度的数字特征。
对南方某市2014年8月份各种气象数据与电力负荷实际值进行了相关性分析。由于采用的历史负荷数据都是夏秋的,所以综合气象因素不考虑寒湿指数。图1显示了南方某市2014年8月29号到31号的每日24点气象因素与该日负荷数据的日相关系数。
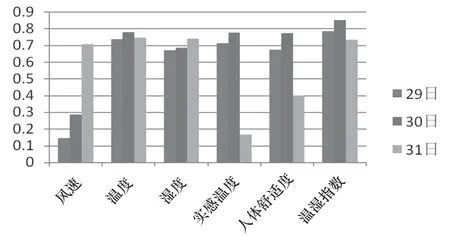
图1 气象因素与电力负荷的日相关系数
由图1可以明显看出单日内温度、湿度和温湿指数与电力负荷的相关性最大且最稳定,风速与电力负荷的相关性较小。而实感温度和人体舒适度的相关性不稳定。其中8月份只有几天有雨,所以降雨量相关性可以忽略。固对降雨量只考虑晴雨天,将其划入日期因素中。对南方某市2014年8月份的气象因素与实际负荷值进行了月相关性分析,如图2所示。
由图2可知8月份在气象因素中温度、温湿指数与负荷的相关性最高。为了验证相关性对选择样本的影响,对8月30日进行了负荷预测,分别对只考虑预测日前30天温度与湿度和加入了风速的方法进行预测。两种预测样本的预测误差如图3所示,可明显看出只考虑温度和湿度的误差反而低于加入了风速的误差。
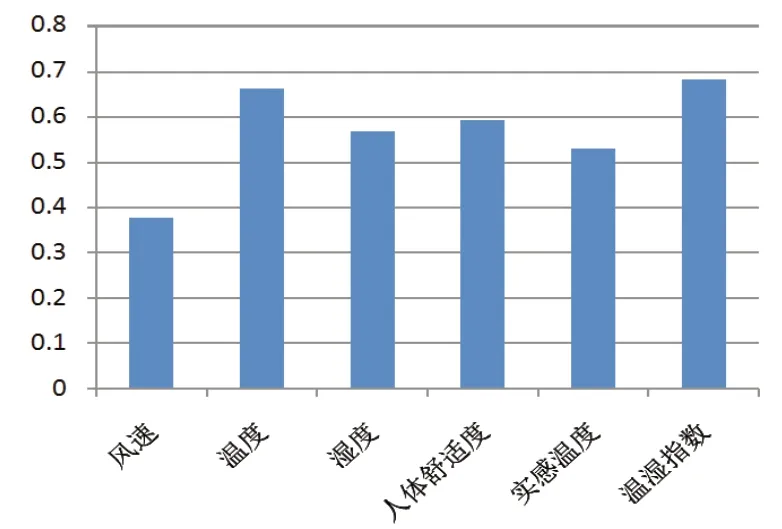
图2 8月份气象因素与电力负荷的月相关性系数
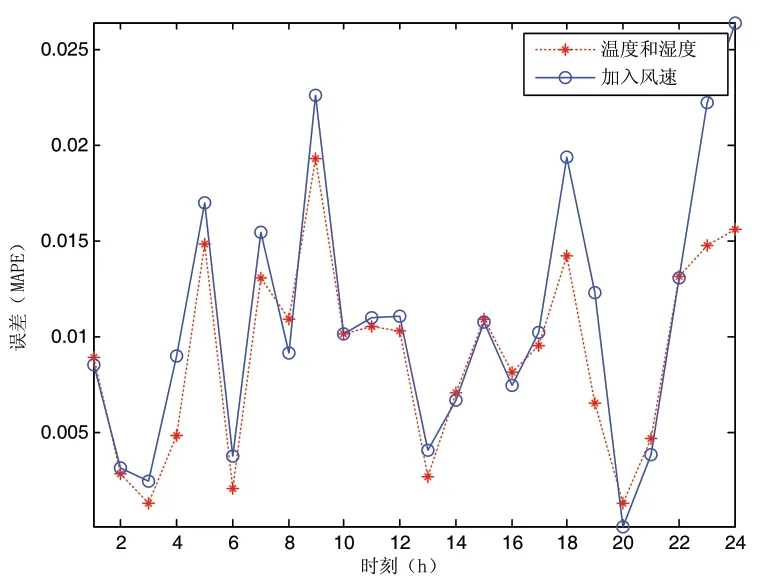
图3 8月30日考虑风速的误差对比
以上实验说明训练样本维数并不是单纯的越多越好,同时验证了相关性分析的有效性。有时候样本维数越多反而预测精度越低,即使是近年来兴起的综合气象指数也不是万能的,并不是每个气象因素在每个季节都是适用的。对于训练样本的选择必须是依据当地气候特征,季节习惯经过严格筛选的,这样才能在增加样本维数的同时提高预测的精度。这就要求进行电力负荷预测时要对当地的气候和季节变化进行分析,从而选择一个适和的气象因素作为训练样本。
1.2 日期因素
力负荷随时间的变化存在一定的规律,其中最突出的就是负荷的日周期性、周周期性和节假日规律。本文将晴雨天也加入到日期因素中,根据对南方某市的负荷与降雨量等因素的分析,对各因素进行了归一化处理。
晴雨天因素:考虑降雨量的多少对负荷的影响,归一化处理后如表1所示。
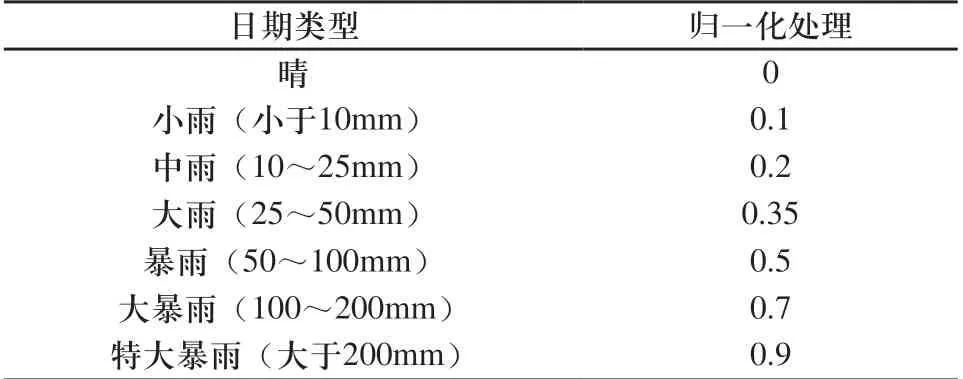
表1 晴雨天归一化
周周期因素:考虑负荷以周为周期进行变化,归一化后如表2所示。
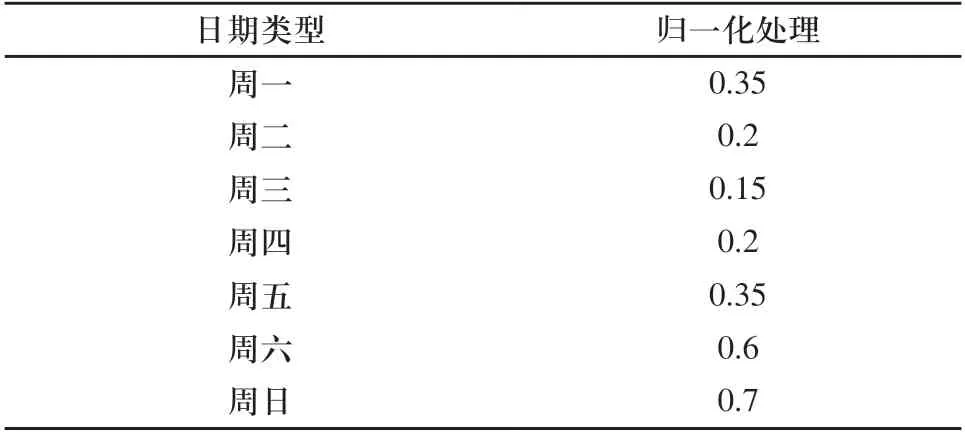
表2 周周期性归一化
2 错位样本
在负荷样本中还有一类特殊的气象样本,它是与日期因素一样每日只有一个数据,就是日平均温度,最低温度和最高温度。在夏季,持续数天的高温天气可能使当日负荷曲线与温度的负荷曲线的拟合度不高,即持续的高温天气和单独一天的高温对该日负荷的影响程度不同,这就是气温的积累效应。有很多原因导致气温积累效应的产生,如持续高温给人们的影响造成民用降温负荷的急剧增加,连续高温干旱导致农用灌溉负荷大幅增加等。
气温的积累效应使得短期负荷预测就要考虑预测日前几天的气象因素的影响。图4为南方某市2014年8月份每日总负荷与平均温度对比图。为了更好的对比,将温度值乘以8再与负荷值进行对比。可以明显看出负荷与平均温度呈跟随性发展趋势。然而因为气温的积累效应的影响,可从图4中可明显看出负荷受前一天气温的影响更大。为了更好的利用负荷与平均温度呈跟随性这一特性,本文引入了错位样本概念。
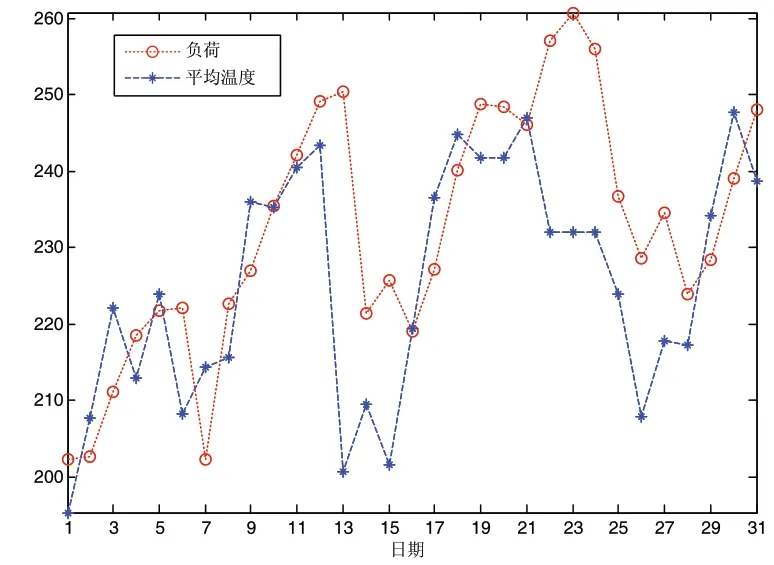
图4 8月份每日总负荷与平均温度对比图
错位样本是指在选择预测时刻前30天气象因素作为预测样本时,将预测日的样本时刻提前n天。即预测m日负荷时,选择m-n日到m-n-30日的气象数据作为训练样本,选择的负荷实际值样本为m-1日到m-31日。图5显示了南方某市8月份每日总负荷与提前1天的错位平均温度对比图。可以明显看出将平均温度提前一天再与负荷进行对比,其拟合度更高。由此可见,将错位样本加入进负荷预测训练样本中是十分必要的。
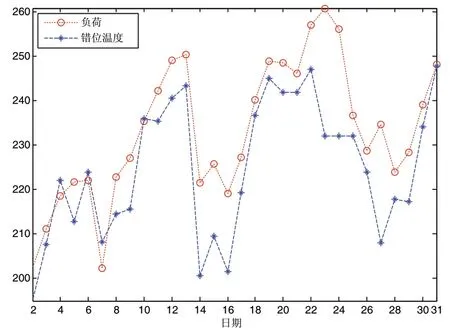
图5 8月份每日总负荷与错位平均温度对比图
然而,错位样本的选择到底提前几天这需要一个评判,本文利用相关性进行选择,取最大的ρn的n为样本的提前天数,其中ρn是提前n天的气象样本和预测样本的相关性系数,由于负荷对温度变化的响应十分迅速,基本在连续高温日的第二天就开始上升,到第三天就可以上升到一个比较高的位置,综合考虑,n取5较为合适。
3 建立LSSVM预测模型
最小二乘支持向量机(LSSVM)是支持向量机的一种扩展,其用等式约束替代了不等式约束同时用损失函数和误差平方作为训练集的经验损失[10],因而把一个带不等式约束的二次规划问题转化为了线性矩阵求解问题。其能以更高精度逼近非线性系统是一种非线性系统的预测方法[11]。其具体原理如下:
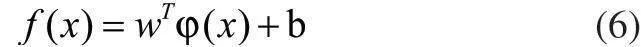
式中:w为n维向量,b为偏差。LSSVM回归算法的优化目标为:
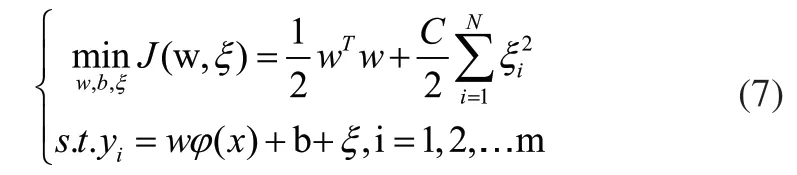
式中:J为误差控制函数;C为误差惩罚函数;ξi为松弛变量。把约束优化问题变成无约束优化问题,定义Lagrange函数:
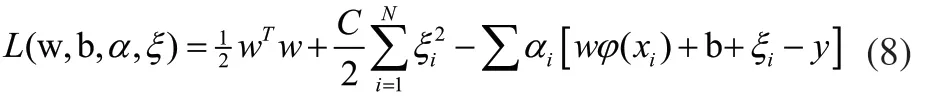
式中:αi为拉格朗日乘子,根据KKT优化条件:
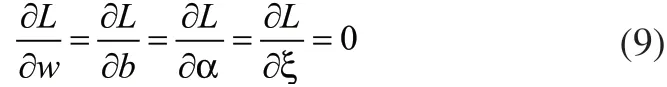
则有:
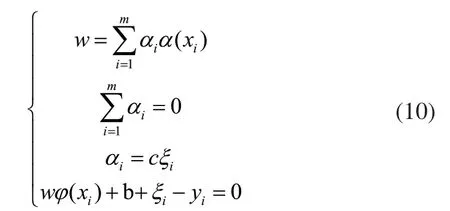
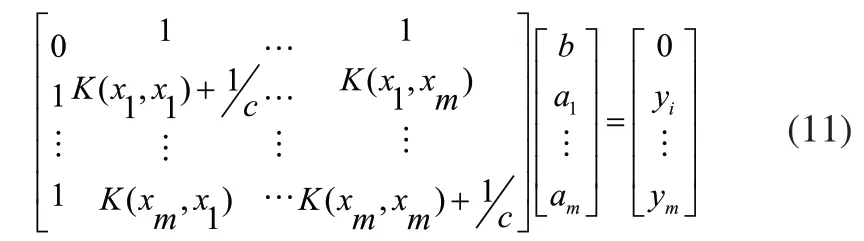
解上述线性方程组可得到拉格朗日乘子am和参数b,则用于函数估计的LSSVM为:
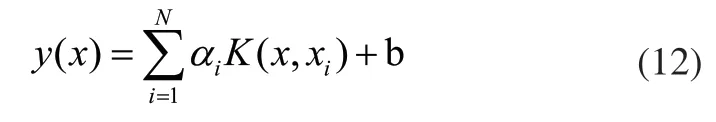
本文采用径向基函数(RBF)作为核函数,上式中:
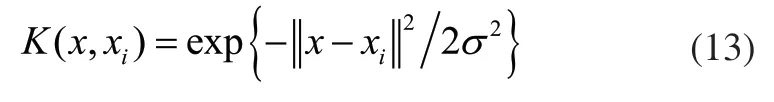
采用径向基核函数LSSVM需确定两个参数,核函数参数σ和惩罚参数C。这两个参数对LSSVM的学习和泛化能力影响很大[12]。
4 算例分析
4.1 样本的选择
预测南方某市2014年8月29日到31日的负荷值。收集了8月的多种气象资料和负荷数据,通过相关性分析选取样本。以29号为例,步骤如下:
1)对29日的气象和负荷进行日相关性分析;
2)对29日前30天的气象和负荷进行日相关性分析;
3)得到日相关和月相关性最高的几个因素,选取其中相同的因素作为样本;
4)确定错位样本提前天数,选择错位样本中相关性最高的气象因素作为样本。
表3显示了预测29日所考虑因素中相关性最高的几个因素。由此选择温湿指数、温度、错位平均温度和日期属性作为训练样本。
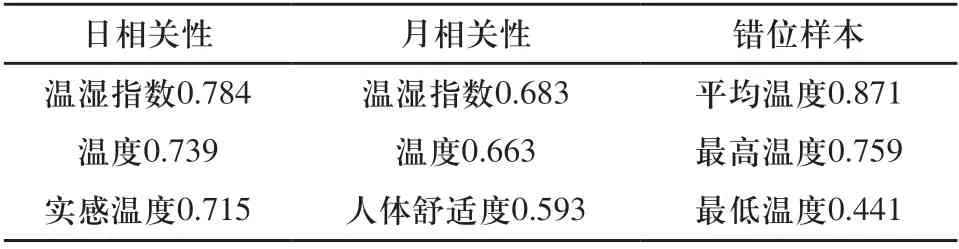
表3 29日预测样本的相关性
4.2 对比仿真
为了验证错位样本和样本选择对预测模型的影响,本文另外进行了两组实验进行对比。第一组不考虑错位样本。第二组即不考虑错位样本也不考虑样本选择。
表4显示了7月29日到31日的每天12点的3种预测方法的负荷预测值对比。可明显看出本文方法的预测结果的平均相对误差仅为0.85%,不考虑错位样本的平均相对误差为1.27%,而即不考虑错位样本也不考虑样本选择的平均相对误差最大为1.8%。本文的方法使预误差减小了近百分之一。

表4 负荷值与实际值对比
5 结论
本文对影响负荷变化的各种因素进行分析,通过各因子与负荷数据的相关性分析来评价各因子对于负荷预测的影响,选取最合适的因素作为训练样本。提出了错位样本概念,利用最小二乘支持向量机(LSSVM)在增大样本维数时不增加计算复杂性的特性,在不降低精度的同时提高速度。用实际数据建立LSSVM模型进行仿真,实验结果表明,通过样本选择的的基于错位样本的负荷预测方法的预测精度明显高于普通的预测方法。并能使预测结果更加的平滑稳定。测试证明了该短期负荷预测方法是有效可行的并具有广阔的发展前景。
[1] 曾鸣,吕春泉,田廓,薛松.基于细菌群落趋药性优化的最小二乘支持向量机短期负荷预测方法[J].中国电机工程学报,2011,31(34):93-99.
[2] 唐聪岚,卢继平,谢应昭,张露.基于改进数据流在线分割的超短期负荷预测[J].电网技术,2014,38(07):2014-2020.
[3] 莫维仁,张伯明,孙宏斌,等.扩展短期负荷预测的原理和方法[J].中国电机工程学报,2003,23(3):1-4.
[4] Bon-Gil Koo, Min-Seok Kim,etc. Short-Term Electric Load Forecasting Using Data Mining Technique[C].Intelligent Systems and Control (ISCO).2013,Coimbatore, Tamil Nadu, India.
[5] 李小燕.考虑气象因素的电力系统短期负荷预测研究[D].华南理工大学,2013.
[6] 钟利华,李勇.综合气象因素对广西电力负荷的影响[J].气象,2008,34(5):31-37.
[7] 李仕峰,钱乐祥,王瑾.基于陆地卫星TM/ETM+改进的温湿指数及其对不透水表面的响应[J].地理与地理信息科学,2013,29(2):112-115.
[8] 张伟.基于人体舒适度指数的配电网短期负荷预测方法[J].电力系统保护与控制,2013,41(9):74-79.
[9] 栗然,郭朝云,韦仲康.京津唐电网电力日峰荷与气象指数的关联性分析[J].电网技术,2008,32(6):87-92.
[10] 梁锦锦,吴德.稀疏L1范数最小二乘支持向量机[J].计算机工程与设计,2014,35(01):293-296,338.
[11] 韩俊英,刘成忠.自适应调整参数的果蝇优化算法[J].计算机工程与应用,2014,50(07):50-55.
[12] 王贺,胡志坚,张翌晖,李晨,杨楠,王战胜.基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J].电工技术学报,2014,29(04):237-245.
