蜘蛛网的结构优化模型研究

赵自强，张二丽

（1.河南教育学院数学与统计学院，河南郑州 450046；2.郑州财经学院计算机系，河南郑州 450000）

蜘蛛网的结构优化模型研究

赵自强1，张二丽2

（1.河南教育学院数学与统计学院，河南郑州 450046；2.郑州财经学院计算机系，河南郑州 450000）

讨论了什么结构的网能够使蜘蛛织网省力又有利于捕食.说明了蜘蛛网的倾角与被捕昆虫的关系并给出了被捕昆虫在不同倾角蜘蛛网上的受力的模型.最后假设蜘蛛准备在一个凸多边形的区域结一张网，针对蛛丝是否连接在支撑点，建立了两种不同的数学模型，并且设计了优化的蛛网结构.

蜘蛛网；蜘蛛结构；蛛网结构优化；数学模型；建模

0 引言

蜘蛛结网是其天生的本领.蜘蛛后端有6个吐丝器，吐丝器外部有1 000多个小孔，从每个小孔分泌出一滴黏液，黏液一遇到空气就变成了硬丝.不同种类的蜘蛛所结网的大小、形状以及网眼疏密等都不相同.在所有蜘蛛网中，都有一个中心点向外辐射蛛丝，其辐射线的数目不同，种类也不同，有21条、32条、42条等.每两根相邻半径间的夹角也是基本相等的，蜘蛛网在数学、力学、经济、医学等方面都有重要应用，可谓昆虫虽小学问却大.

假设一只昆虫的质量为0.325 g，蜘蛛牵引丝的原始标距长度为l0，杨氏模量为E，昆虫的横截面积为A，重力加速度为10 g/m，昆虫的质量与最大力量的比值范围为0＜k＜1，提出以下问题：

1）在理想条件下，蜘蛛可以分别织出方形蜘蛛网、同心圆蜘蛛网和螺旋蜘蛛网.比较它们的面积大小，探讨什么形状的网更有利于蜘蛛捕食.

2）在自然条件下，蜘蛛网捕获昆虫受众多因素的影响，建立昆虫对蜘蛛网的作用模型.蜘蛛网与被捕昆虫的最优关系，通过受力分析，求出蜘蛛网倾角与被捕昆虫在网上受力的最优情况模型.

3）通过分析蜘蛛网的圈数和捕获昆虫的关系，说明什么样的蜘蛛网间距最合适，并给出可行性分析.

4）假设有一个凸多边形的区域，蜘蛛准备在这个区域（或其一部分）上结一张网.第一种情况，在区域的边界上安置有若干支撑点，蛛丝可以连接在支撑点上，不能连接到区域边界的其他点，建立合理的数学模型，对不同的情况都设计出合理的蛛网结构.第二种情况，如果蛛丝可以连接在区域边界的任何点上，建立合理的数学模型，设计出合适的蛛网结构.通过这两种情况更加具体地了解蜘蛛结网的优化模型.

1 模型假设

1.1 模型1的假设

1）蜘蛛可以分别织出方形蜘蛛网、同心圆蜘蛛网和螺旋蜘蛛网；

2）蛛网的最优模型是螺旋线形.

1.2 模型2的假设

1）假定在蜘蛛的正常捕食范围内，假设不存在除猎物外的生物或者其他因素造成网的震荡或破坏.在实际问题中，蜘蛛网的牢固性受其他生物、风向、气候的变化，以及人为因素的各种影响，而忽略以上各种因素的影响，仅仅考虑昆虫对蜘蛛网的作用.

2）忽略蜘蛛结网成丝的速度与方式和蜘蛛丝力学性能的关系［1］.

3）昆虫质量和它的最大力量成正比.

4）蜘蛛网与被捕昆虫的最优关系，受力分析，求出蜘蛛网倾角与被捕昆虫在网上受力的最优情况模型.

1.3 模型3的假设

1）在蜘蛛力所能及的范围内织一张网.假定在蜘蛛的正常捕食过程中，不存在除猎物外的生物或者其他因素造成网的震荡或破坏.在实际问题中，蜘蛛网的牢固性受其他生物、风向、气候的变化，以及人为因素的各种影响，而忽略以上各种因素的影响，仅仅考虑昆虫对蜘蛛网的作用.

2）假设蜘蛛网的面积一定，判断昆虫是否会从间隙飞过，若能飞过则蜘蛛还需织网，若昆虫飞不过，则不需要蜘蛛再织网，此时的间距即能满足蜘蛛最大程度捕食到食物，又能满足蜘蛛用丝最省.

3）假设昆虫的最大截面为一圆形.

1.4 模型4的假设

1）假设有一个凸多边形的区域，外界条件影响忽略；

2）假设蜘蛛网的纬线是由直线组成，且各条纬线满足相互平行、等间距的条件；

3）认为蜘蛛网的结构形式是关于原点呈中心对称的；

4）假设昆虫撞击到蜘蛛网的任何部位是一个随机事件.

2 符号说明

L为周长，S为面积，R0为圆的半径，r0为螺旋线初始半径，F0为昆虫挣脱网的最大负荷，A为昆虫横截面积，m为昆虫的质量，T为昆虫的最大力量，k为昆虫的质量与最大力量的比值，l0为蜘蛛牵引丝的原始标距长度，l为蛛丝变形后的长度，σ为应力，ε为应变，g为重力加速度，θ为蛛网与水平线的夹角，r为昆虫的横截面半径，R为蜘蛛网的外层半径，F为昆虫挣脱网的最大负荷，E为杨氏模量，为最内层螺旋线的半径，n为螺旋线的层数，Y为牵引线的条数，f为单根螺旋线的最大附着力，f0为单根牵引丝的最大承受力，h为纬线平行间距，N2为纬线根数，λ为能够粘住半径为r的昆虫的螺旋丝的条数，η为能够承受半径为r的昆虫撞击的牵引丝的条数，N1为辐线根数（辐线：从中心向外发散的网线）.

3 模型的建立与求解

3.1 模型建立

3.1.1 模型1

周长一定的平面封闭图形以圆的面积最大.所以当面积一定的网织成圆形时蜘蛛所吐的丝最少，织网最省力.但是蜘蛛不可能按照既定的圆来织网，而且自然界中蜘蛛织网通常是螺旋线状.所以同心圆网最终改进为螺旋线网，其最外层螺旋线趋于圆，既保证了最少蛛丝最大覆盖面积，又保证了织网的流畅性和可操作性（表1）［2］.

表1 周长一定的方形网与圆形网面积比较Tab.1 The area com parison of square and circu lar w ith fixed perim eter

3.1.2 模型2

由于蜘蛛网受到昆虫的撞击，使得蛛网受到一定的作用力，当昆虫挣脱网的负荷达足够大时，网的最大负荷也足够大，则蜘蛛丝的变形长度很大，直到一个极限值，蜘蛛丝断裂.根据三角关系知，角度也将达到一个不稳定状态，即蜘蛛网就会破损.由此建立模型，利用数学关系、应力应变关系、三角形知识综合检验昆虫对蜘蛛网的影响作用［3］.

3.1.3 模型3

由于蜘蛛织网的稠密度不同，因而建立一张“内松外紧”式螺旋线网.假定蜘蛛分泌丝的速度一定，讨论在网的半径和被捕昆虫大小一定的情况下，螺旋线的最少圈数和牵引丝的最少条数.

3.1.4 模型4

根据两点可以确定一条直线，在一个给定的多边形区域建立3种不同的蜘蛛网模型.假设蛛丝可以连接在区域边界的任何点上，通过连接凸多边形的支撑点和区域边界的任何点，建立模型并通过数学方法计算得出可接受的最不利捕食路径长度.

3.2 模型求解

3.2.1 什么形状的网更有利于蜘蛛捕食

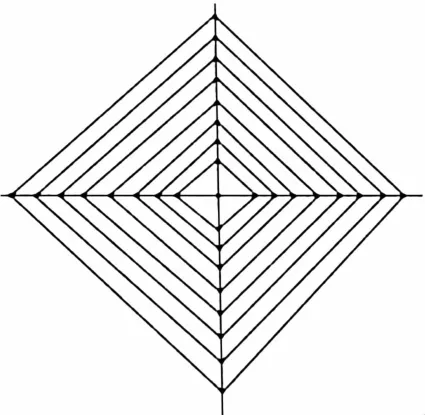
图1 方形网Fig.1 Square web

图2 同心圆网Fig.2 Circular web

再比较图3和图4，根据蜘蛛织网的规律性和可行性可知，图4为最优模型，也是本文的核心模型.由以上分析可知，螺旋蜘蛛网具有可操作性、织网流畅性.

图3 螺旋网Fig.3 Sp iral w eb

图4 多边形螺旋网Fig.4 Polygon spiral web

3.2.2 求出蜘蛛网倾角与被捕昆虫在网上的受力模型

由昆虫的最大力量与它的质量成正比可知T=kmg.一般蛛丝的伸长率为0.01～0.03，这里为了更能说明问题，取最大伸长率0.03，昆虫挣脱网的最大负荷

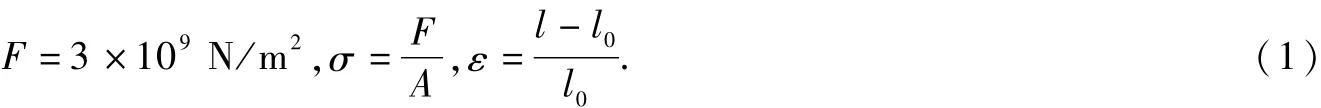
当昆虫撞击蜘蛛网时，会在丝拉索上形成直角冲击负荷，由于拖丝和鞭毛丝均具有高韧度，两者的平衡阻滞约为65%.即昆虫飞行时所具有的动能约有65%被吸收转化为热量，因而不致于使昆虫通过反弹作用被弹出蜘蛛网［4］.对网的切平面受力分析（图5）可得

即可知角度与昆虫在倾斜网面上的关系，亦可知结网的最佳角度.

图5 昆虫网上受力分析图Fig.5 Analysis of force app liedto insects arrested

图6 “内松外紧”式螺旋线网Fig.6 Spiral w eb w ith tight inside and loose outside

3.2.3 分析蜘蛛网的圈数和捕获昆虫的关系

当蜘蛛网的外层半径为R时 3.2.4 只连接支撑点的蛛网模型

在区域的边界上安置有若干支撑点，蛛丝可以连接在支撑点上，不能连接到区域边界的其他点.第一种方法利用边界法，找到中心依次连接中心和各支撑点，顺时针依次连接各支撑点，以这些支撑线段作等分点建立模型（图7）.第二种方法找到中心依次连接中心和各支撑点，通过连接各支撑点相邻或相间的各支撑点建立模型（图8）.

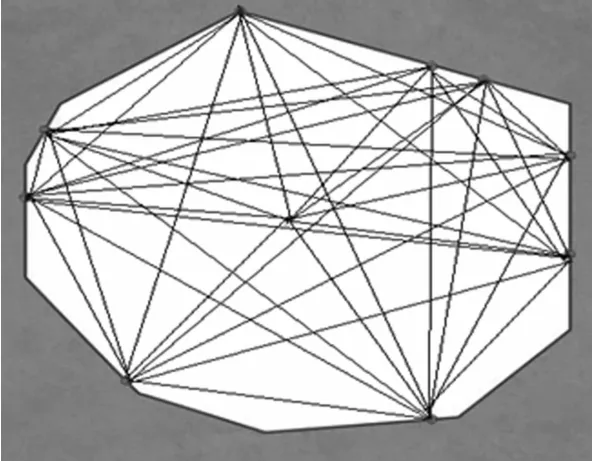
图8 互连支撑点与中心点模型Fig.8 Interconnection m odel for supporting and center poin ts

3.2.5 连接区域边界任何点的蛛网模型

图7 边界法模型

Fig.7 Boundary m ethod m odel，平均最不利路径长度

图9 蛛网模型图Fig.9 Spider web m odel

图10 剖面图Fig.10 Profile im age

通过带入数值计算得出蜘蛛网结构辐线N1数目的最优值范围在20至30，纬线N2数目的最优范围数在15至25.根据控制变量法，当辐线数为27时，纬线数为16，此时得出可接受的最不利长度是89.45 cm.

4 模型的优缺点与推广

4.1 优点

利用简单的蜘蛛网结构模型分析复杂的蜘蛛网问题，采用多种方法进行，使之越来越完善，具有一定的普遍性.对模型作进一步讨论便可得到一系列可靠的实用信息，所得结论与客观事实吻合，从而说明了模型的合理性.模型具有普遍性和可推广性，只要给出的数据充足、精确，模型得出的最优解将具有很强的实际意义.

4.2 缺点

由于受到环境条件（风向、温度、湿度、昆虫的大小、地理位置）等影响，蜘蛛网的易破损程度不同，对于已知条件中的信息分析力度还不够，有些信息没有考虑，再加上数据本身的误差使得结果的精度有待提高，小数点后的省略也使得实际情况不容易达到.网的倾斜使得水平覆盖面积减小，进而影响蛛网的捕食量，还有待改进.

4.3 模型的推广

此模型具有普遍性和可推广性，只要给出的数据充足、精确，模型得出的最优解将具有很强的实际意义.模型可用于捕鱼，建立最有利的捕鱼网，在一定程度上促进了捕鱼业的发展.

［1］ 刘敏，潘志娟，李春萍.成丝的速度与方式和蜘蛛丝力学性能的关系［J］.东华大学学报：自然科学版，2005，31（5）：11-15.

［2］ 潘志娟，盛家镛，戴宏钦.蜘蛛丝的结构与力学性能［J］.南通工学院学报，1999，15（2）：6-8.

［3］ 吴建国.数学建模案例精编［M］.北京：中国水利水电出版社，2005：310-381.

［4］ 刘庆生，段亚峰.蜘蛛丝的结构性能与研究现状［J］.四川丝绸，2005（2）：16-18.

Research on Structure Optim ization M odel of Spider W eb

ZHAO Zi-qiang1，ZHANG Er-li2

（1.School of Mathematics and Statistics，Henan Institute of Education，Zhengzhou 450046，China；2.Department of Computer，Zhengzhou Institute of Finance and Economics，Zhengzhou 450000，China）

What kind of web structures can make spider weave web and prey easily is discussed.The relationship between the inclination of cobwebs and arrested insects is illustrated，and the force of the spider web model for insects arrested in different angle is presented.Finally，supposing the spider in a convex polygon region to weave a net，two different mathematical models and optimization structure of spider web are given under the conditions whether spider silk is connected at anchor or not.

spider web；structure of spider web；structure optimization of spider web；mathematicalmodel；modeling

O141.4

A

1007-0834（2015）03-0001-06

10.3969/j.issn.1007-0834.2015.03.001

2015-05-09

河南省哲学社会科学规划项目（2014BJY026）；河南省高等教育改革研究项目“数学教育专业课程体系与教学内容整体化研究与实践”（2014SJGLX499）；河南教育学院应用数学重点学科资助项目

赵自强（1981—），男，河南沈丘人，河南教育学院数学与统计学院讲师.