“走进图形世界”测试卷

李中栋

一、 选一选

1. 在棱柱中（ ）.

A. 只有两个面平行 B. 所有的棱都平行

C. 所有的面都是平行四边形 D. 两底面平行，且各侧棱也互相平行

2. 下列平面图形不能够围成正方体的是（ ）.

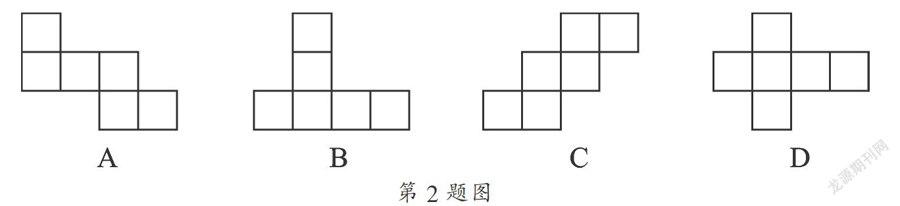
3. 下列图形是四棱柱的侧面展开图的是（ ）.

4. 将一个正方体沿着某些棱剪开，展成一个平面图形，至少需要剪的棱的条数是（ ）.

A. 5 B. 6 C. 7 D. 8

5. 下列图形中，不是三棱柱的表面展开图的是（ ）.

6. 圆柱是由长方形绕着它的一边所在直线旋转一周所得到的，那么下列左图是以下四个图中的哪一个绕着直线旋转一周得到的（ ）.

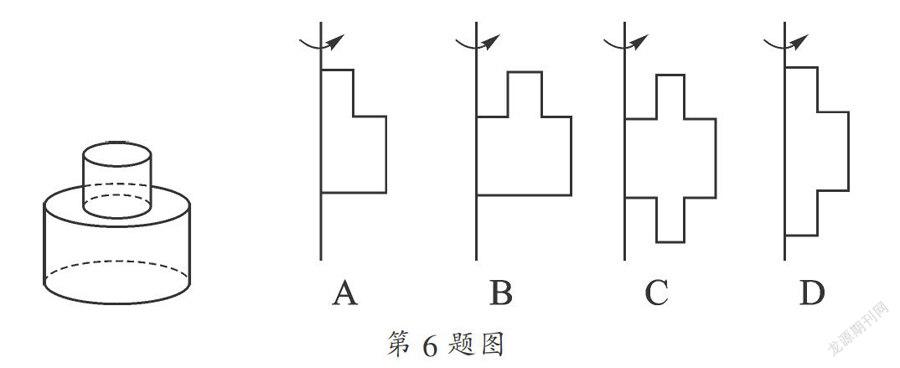
7. 如图是一个立体图形的三视图，这个立体图形是由一些相同的小正方体构成，这些相同的小正方体的个数是（ ）.

A. 4 B. 5 C. 6 D. 7

8. 若一个立体图形的主视图与左视图都是等腰三角形，俯视图是圆，则这个立体图形可能是（ ）.

A. 圆锥 B. 三棱柱 C. 圆柱 D. 三棱锥

9. 一个四棱柱被一刀切去一部分，剩下的部分是（ ）.

A. 三棱柱 B. 四棱柱

C. 五棱柱 D. 以上都有可能

10. 如图，下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么涂黄色、白色、红色的对面分别是（ ）.

A. 蓝色、绿色、黑色 B. 绿色、蓝色、黑色

C. 绿色、黑色、蓝色 D. 蓝色、黑色、绿色

二、 填一填

11. 如果一个几何体的三种视图之一是三角形，这个几何体可能是_______（写出1个即可）.

12. 将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，应剪去_______（填序号）.

13. 几何体中主视图是圆，左视图和俯视图都是长方形，该几何体是_______.

14. 在桌上摆有一些大小相同的正方体木块，其主视图和左视图如图所示，则要摆出这样的图形至少需要_______块正方体木块.

15. 一个棱锥有7个面，这是_______棱锥，有_______个侧面.

16. 用六根长度相等的火柴棒搭等边三角形，最多搭成_______个.

17. 下列第二行的哪种几何体的表面能展开成第一行的平面图形？请对应填空.

①：______________；②：______________；③：______________；④：______________；⑤：_____________.

三、 解一解

18. 如图是一个正方体骰子的表面展开图，请根据要求回答问题：

（1） 如果1点在上面，3点在左面，几点在前面？

（2） 如果5点在下面，几点在上面？

19. 如图是一个由若干个小正方体搭成的几何体的俯视图，其中小正方形格内的数字是该位置小正方体的层数，请你画出它的主视图和左视图.

20. 画出下列几何体的三视图：

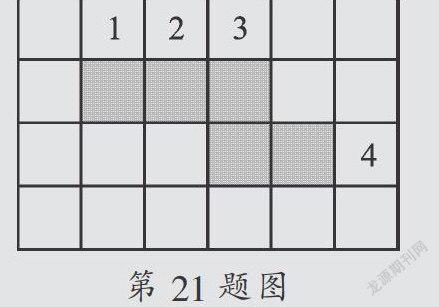
21. 如图，某同学在制作正方体模型的时候，在方格纸上画出几个小正方形（图中阴影部分），但是由于疏忽少画了一个，请你给他补上一个，使之可以组合成正方体，你有几种画法，在图上用阴影注明.

22. 如图是一个正方体的平面展开图，若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和均为5，求x+y+z的值.

参考答案

1. D 解析：对于A，如果是长方体，可能不止有两个面平行，故错；

对于B，如果是长方体，不可能所有的棱都平行，只是所有的侧棱都平行，故错；

对于C，如果是底面为梯形的棱柱，不是所有的面都是平行四边形，故错；

对于D，根据棱柱的定义知其正确，故选D.

2. B 解析：利用自己的空间想象能力或者自己动手实践一下，可知答案选B.

3. A

4. C 解析：如果把一个正方体剪开展平的图画出来，发现有5条棱没剪（没剪的棱为两个正方形的公共边），正方体总共12条棱，∴ 12-5=7（条）即为所需剪的棱.

5. D 解析：A、B、C中间三个长方形能围成三棱柱的侧面，上、下两个三角形围成三棱柱的上、下两底面，故均能围成三棱柱，均是三棱柱的表面展开图. D围成三棱柱时，两个三角形重合为同一底面，而另一底面没有，故D不能围成三棱柱.

6. A 解析：根据选项中图形的特点，

A. 可以通过旋转得到两个圆柱，故本选项正确；

B. 可以通过旋转得到一个圆柱，一个圆筒，故本选项错误；

C. 可以通过旋转得到一个圆柱，两个圆筒，故本选项错误；

D. 可以通过旋转得到三个圆柱，故本选项错误.

7. D 解析：如图，由已知中的俯视图，我们可得：

该立体图形共有五摞小正方体组成，

由主视图我们可知，第1摞只有一个小正方体，

由左视图我们可知，第3和第5摞也只有一个小正方体，只有2、4两摞各有两个小正方体.故这些相同的小正方体共有7个.

8. A 解析 A. 圆锥的三视图分别是等腰三角形、等腰三角形、圆及一点，符合题意；

B. 三棱柱的三视图分别是长方形、长方形、三角形，不符合题意；

C. 圆柱的三视图分别是长方形、长方形、圆，不符合题意；

D. 三棱锥的三视图分别为三角形、三角形、三角形及中心与顶点的连线，不符合题意.

故选A.

9. D 解析：三棱柱、四棱柱、五棱柱都有可能，故选D.

10. B 解析：分析可知黄色的对面是绿色，白色的对面是蓝色，红色的对面是黑色.

11. 圆锥 四棱锥 三棱柱

12. 1或2 解析：根据有“田”字格的展开图都不是正方体的表面展开图可知，应剪去1或2，答案不唯一.

13. 圆柱 解析：几何体的左视图和俯视图都是长方形，主视图是圆，符合这个条件的几何体只有圆柱.

14. 6 16 解析：易得第一层最少有4块正方体，最多有12块正方体，第二层最少有2块正方体，最多有4块正方体，故总共至少有6块正方体，至多有16块正方体.

15. 六，6 解析：一个棱锥有7个面，这是六棱锥，有6个侧面.

16. 4 解析：如图，用六根长度相等的火柴棒可以搭成如图中三棱锥的形状，所以最多搭成4个等边三角形.

17. D，E，A，B，C

18. 解：（1） 如果1点在上面，3点在左面，那么2点在前面.

（2） 如果5点在下，那么2点在上.

19. 分析：从俯视图可以看出该几何体有三行、四列，以及每行（每列）的最高层数.因而在主视图中共四列，（自左到右数）第一列最高一层，第二列最高两层，第三列最高三层，第四列最高一层，从而确定主视图的形状.在左视图中共三行，（自前到后数）第一行最高三层，第二行最高两层，第三行最高一层，从而确定左视图的形状.

解：主视图和左视图如图所示.

20. 解：三视图如图所示.

21. 解：画图如图所示，共有四种画法.

22. 解：由于正方体的平面展开图共有六个面，

其中面“z”与面“3”相对，面“y”与面“-2”相对，面“x”与面“10”相对，

则z+3=5，y+（-2）=5，x+10=5，解得z=2，y=7，x=-5.故x+y+z=4.

（作者单位：江苏省南师附中江宁分校）