提高高中学生物理计算能力的策略
2015-09-10刘爱民
刘爱民
高中物理对大多数人来说是很难学的,这是毋庸置疑的。整个高中物理是比较抽象的,而且都是定量的,计算要求比较高,所以要学好高中物理,正确的方法与技巧是必不可少的,甚至是致命的,对此作为一名物理教师,笔者针对物理计算能力如何提升的问题谈谈自己的观点:
1.全面、深入、准确地理解物理概念、物理规律
物理学科的知识点都是有规律的,例如:对力的概念的理解包括对具体的力(重力、弹力、摩擦力、电场力、安培力、洛仑兹力等)的概念的理解,包括对一般抽象的力的概念的理解,还包括力作用于物体产生不同效果的理解,等等。我们需要从不同角度理解力的概念,在繁杂的力学问题中,在带电粒子在电场和磁场的运动问题中,遇到各种各样的力,通过这些问题不断加深对不同性质的力的理解,不断加深对抽象的、普遍的力的概念的理解。如静摩擦力可使物体加速,也可使物体减速,可以做正功、做负功、不做功,但一对静摩擦力总不做功(做功代数和为零)。洛仑兹力的方向总跟速度垂直,总不做功,它只改变速度方向不改变速度大小,这是洛仑兹力的最大特点,其他力都不具有这一特点。力产生加速度,反之如果发现物体有加速度就判定一定有力产生等。深刻理解这些概念和规律后才能准确找到合适的公式进行计算,“一针见血”解决问题,而不再乱套公式,避免发生算来算去都不知道自己要算什么的尴尬现象。
2.巧用利用数学知识解决物理问题
物理学科具有自己独特的特点,不是单纯的理论学科,也不是单纯的计算学科,注重与生活紧密联系,以数学计算方式为基础探究更深层次的规律。所以利用好数学的各种原理,再难的物理问题也会迎刃而解。
2.1用相似三角形解物理问题
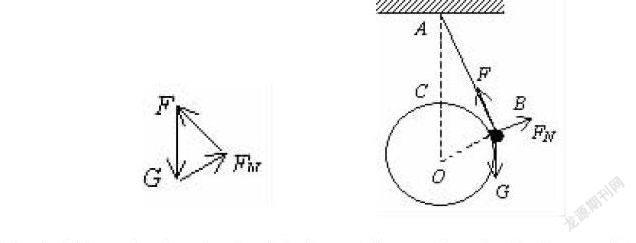
相似三角形法通常寻找的是一个矢量三角形与一个几何三角形相似[1]。利用相似三角形对应边的比例关系求解力的大小,特别当几何三角形的边长已知时。例题:如图1-1所示,轻绳的A端固定在天花板上,B端系一重为G的小球,小球静止在固定的光滑大球表面上,已知AB绳长为l,大球半径为R,天花板到大球顶点的竖直距离AC=d,角ABO>90°。求绳中张力和大球对小球的支持力。(小球直径忽略不计)
【解析】:选小球为研究对象,受到重力G、绳的拉力F和大球支持力F■的作用(如图1-1)。由于小球处于平衡状态,因此G、F、FN组成一个封闭三角形。根据数学知识可以看出三角形AOB跟三角形FGF■相似,根据相似三角形对应边成比例得F/L=G/(d+R)=F■/R,解得F=G·L/(d+R) F■=G·R/(d+R)。由此可见,当绳长L减小时,F变小,FN不变。
2.2二次函数的利用
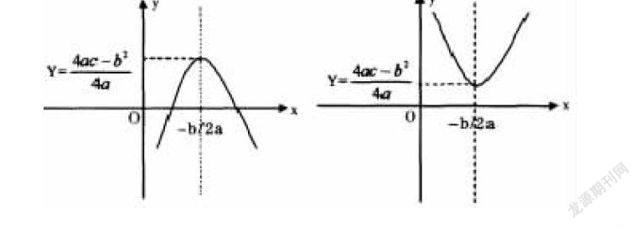
二次函数在运动中有很多应用,有时它可以省去物理情境的讨论,以不变应万变,对物理情境一时难想象的同学此方法可作为一种选择,对理解运动中物理情境有一定的帮助。二次函数y=ax■+bx+c的图像是抛物线,当a<0时,抛物线开口向下,当x=-■时,y有极大值,为y■=■;当a>0时,抛物线开口向上,当x=-■时,y有极小值,为y■=■;如图所示当y=0时图像与x轴相交,其交点为ax■+bx+c=0的两解,无交点则表示无解。
运动学中两追击物体间的距离△s刚好就是时间t的二次函数。若物体1追物体2,设两物体开始相距的距离为s0,则两物体间距离为:△■=s■+s■-s■=■(a■-a■)t■+(v■-v■)t+s■。这可用运动学追击问题中的相距最远(最近)和是否相遇及相遇时间等问题。其图像与x轴的两个交点是追击过程中的两个相遇点,若图像与x轴无交点,则不可能相遇,这可用判别式△=■是否大于或等于零来判定:若判别式大于零有两个解,表示相遇两次;若判别式等于零,图像和x轴有且只有一个交点,即顶点在x轴上,表示追击过程中只相遇一次;若判别式小于零,图像与x轴无交点,表示不可能相遇。
3.程序化教学
物理教学中采用程序教学思想,即针对物理课堂的教学任务,设置学生熟悉的情景,在这个情景中通过一系列层次分明的问题,引导学生思考,最终通过学生的一系列学习行为获得最后预期的教学效果。教学时把程序教学思想应用到物理现象、物理概念、物理规律、物理习题教学中,同时在作业中设置程序化问题,让学生通过自我思考成功得出结论。程序教学能有效提高学生的解题能力和分析问题、解决问题的能力。能力的提高是解决计算困难的根本途径[2]。
综上所述,提高计算能力不是一朝一夕的事情,学生要持之以恒,教师要不断地提示、引导,在师生的共同努力下,提高计算能力不再是梦,高中物理也不再是学生的“噩梦”,教育是不断探索的过程,笔者的观点只代表一部分观点,难免有片面性,希望进一步与同行们交流探讨。
参考文献:
[1]曹伟达.三角形相似法在高中物理中的应用.中学物理,2012(09):57.
[2]陈宁,王怡菲.斯金纳程序教学在现代教育中的作用.九江学院学报,2006(04):140.
