“变教为学”需要“诱人”的问题

“变教为学”教学改革意欲将学生的学习方式从“被动接受式”改变为“主动生成式”；将教师的教学方式从“讲授式”改变为“引发式”。其中“引发”的含义包括“引导学生专心，激励学生努力，诱导学生愿意”。为此，教师就需要在备课中为学生设计能够“吸引注意、焕发勇气、激发动机”的情境与问题。这种“诱人”的问题的开发与设计，是“变教为学”教学改革研究的一项重要内容。

“诱人（Engagement）”的情境与问题的一个特征应当是“真实（Authentic）”，也就是问题应当来源于真实发生的社会活动或者自然现象中人的某种需求，历史上许多这样真实的问题吸引了数学家们的注意并开展研究，因此导致了数学中重大的发现或者发明。

比如，在18世纪的欧洲，普瑞格尔河（Pregel River）流过东普鲁士（East Prussia）的古城哥尼斯堡（Konigsberg）市中心，河两岸分别是图1的B处和C处，流经两个小岛分别是图1中的A处和D处，连接两岸和小岛之间筑有七座古桥（见图1）。每逢节假日，市民们纷纷上岛游玩散步。凡旅游者都有一种愿望，游览的景点尽量多，而且不走重复路。渐渐地，人们发现这七座桥不能满足这一愿望。要想走遍七座桥，就一定有桥重复走，不重复就不能走遍七座桥。这就刺激人们产生了解决下面问题的愿望：寻找一条行走路线，使得每座桥都走到，并且每座桥只走一次。这一问题曾经吸引了无数人的研究兴趣，最终由当时在彼得堡科学院工作的瑞士数学家欧拉（Leonhard Euler，1707～1783）成功解决，并在此基础上创立了数学的一个分支——“图论”。[1]

这一问题被后人称为“七桥问题”，“七桥问题”之所以诱人，从客观的角度看，是人们在日常活动中遇到的真实的事情，从主观的角度看，正是人“占有更多”和“简捷省力”的愿望，导致了人们具有解决这个问题的需求。因此可以说“诱人”的问题仅有“真实”的特征是不够的，还应当与问题解决者的愿望或者需求有联系。

比如，在用现金购物的活动中，人们经常会出现需要“找零”的情况，对于商家来说有时会出现缺少零钱而不能实现找零的窘境。因此就会出现下面的情境与问题。

例题1：某件商品17元，顾客付款20元，商家应当找回零钱3元。如果此时商家恰好没有3元零钱，那么有什么办法可以解决这个问题呢？

这样的问题来源于日常活动，反映了人们在社会活动中的需求，应当说具有“诱人”的特征。问题的解决至少可以有两个方案，第一是如果商家此时有5元纸币，顾客有2元零钱，那么就可以请求顾客再付2元，而后商家找还给顾客5元。思考过程中需要的计算包括：

20-17=3（元）

20+2-17=5（元）

第二个方案与此类似，如果商家此时没有5元纸币，但有10元纸币，顾客恰好有7元零钱，那么就可以再付给商家7元，商家找还10元即可。用到的算式为：

20+7-17=10（元）

以上过程在实际教学中，不需要教师对解决方案进行讲解。教师可以通过“讲故事”或者“视频”的手段，向学生展示情境的发生与发展，而后组织学生思考并讨论诸如下面的问题：

要解决的问题是什么？

可以怎样解决？

解决过程用到了哪些知识和方法？

其中“要解决的问题是什么”的思考与讨论，目的是引导学生经历“发现问题、理解问题、表达问题”的过程。也就是让学生在这个思考和讨论的过程中，能够感受到问题的存在，理解问题的含义，能够用自己的语言表述。

对于“可以怎样解决”这一问题，其实是引导学生经历对于解决问题的过程与方法的设计过程。这一过程期望学生对每一个解决方案进行细致思考，以及对不同方案的交流和比较。

关于“解决过程用到了哪些知识和方法”的思考，其实是对解决问题后的反思或总结的过程。前面问题的解决实际上运用的是“凑整”的方法，是在减法运算中为减法的结果“凑五”或“凑十”，用到了减法的一个运算规律，即“如果减数不变，那么被减数增加或减少多少，差也增加或减少多少”。用算式表达出来就是：

（a+c）-b=（a-b）+c

（a-c）-b=（a-b）-c

由于这一问题的解决所用到数学知识相对简单，因此适合于低年级的计算以及解决问题的教学。而在中年级学生学习混合运算时，可以引导学生研究下面的问题。

例题2：学校每天上午上4节课，每节课40分钟。上午的一次课间为课间操，时间为30分钟。其余课间休息每次时间为10分钟。如果早晨第一节课8点整开始，那么上午最后一节课什么时间结束？

这一问题显然与学生每天在学校的活动息息相关，自然会唤起学生愿意去思考并解决的愿望。思考过程会用到“倒推”的思路，为了知道“什么时间结束”，需要知道“共用多少时间”；为了知道共用多少时间，先要知道“上课共用时间”和“课间共用时间”。这样的思考过程可以用图2的流程图直观表现出来：

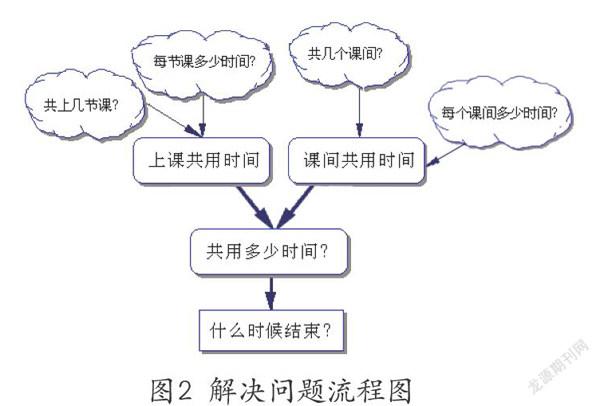
有了以上分析，就可以通过计算解决问题了。因为一个上午共4节课，每节课40分钟，因此一个上午“上课共用时间”为：

40×4=160（分）

又因为共有3次课间，其中2个每次是10分钟，另一个是课间操需要30分钟，所以课间共用时间为：

10×2+30=50（分）

所以共用时间为：160+50=210（分）

核算出210分钟是3个半小时，因此从8点开始上课，到最后一节课结束共经过3个小时30分钟，因此最后一节课结束时间应当是上午11点半。

实际教学中，重点是引导学生对问题进行分析和转化。也就是要引导学生理解下面这些问题，并且理清这些问题之间的关系：

最后一节课什么时候结束？

从早晨8点开始上课，到最后一节课结束共经过多少时间？

上课共用多少时间？

课间共用多少时间？

一个上午一共上几节课？

一节课多少分钟？

一个上午有几次课间？

每个课间多少分钟？

问题的解决过程中，不仅要用到混合运算的知识与方法，而且还用到了“植树问题”的模型。在“一个上午有几次课间”这个问题的思考中，因为一个上午共有4节课，因此其中会出现3次课间，这实际上就是“植树问题”的模型。（见图3）

学生学习数学的过程，对于数学知识是分门别类进行学习的。而在解决实际问题的时候，知识的应用往往是综合的，这就需要学生逐步形成一种能够甄别、选择和使用所学知识的能力。为了锻炼这种能力，就需要给学生更多这样的机会去经历和体验。

在人的日常活动中往往有对于“日期”和“星期”相互转换的需求，比如：

例题3：在不查看日历的情况下，如何能够迅速知道2015年12月18日是星期几？

对于这一问题的思考，所依据的基本原理是数学中的“余数”。观察日历表可以发现12月18日的星期数与12月4日、11日、25日的星期数是一样的，原因是4、11、18、25除以7的余数相同。由于这四个日期数均匀分布于整月中，因此，有一种方法就是利用所熟悉的特殊日期进行推算，比如，如果12月6日恰好是自己或亲朋好友的生日，因此对于12月6日是星期日印象深刻，由此推算12月4日是星期五，因此12月18日也是星期五。

另外一个简便的方法是记住12月第一个星期日的日期数，比如2015年12月第一个星期日的日期数是6日，从6日开始过1天是7日，就是星期一，过2天是8日，就是星期二，依次类推，从6日开始算起，经过几天就是星期几。因此要想求出18日的星期数，只要用18减去6的结果为12，说明从6日到18日共经过12天。用12除以7，余数为5，说明经过12天与经过5天的星期数相同，因此5就是18日的星期数，即星期五。

在小学数学课程中有“探索规律”的课程内容，所谓“探索规律”就是在运动与变化的过程中寻找不变因素，[2]一旦发现这样的不变因素，就意味着发现了规律，进而就可以实现“预见未来（Prediction）”的目的。如果把从12月6日到12月18日的变化过程用图4表示出来，就可以明显地看出这样的规律：

实际教学中，应当引导学生把注意力放在运动与变化上，以及其中蕴含着的不变因素方面。在图4的变化过程中存在着两个不变因素，第一是从6日开始过几天就是星期几（天数比8小的时候），比如过5天是11日恰好是星期五；第二是从任何一天经过7天的星期数是相同的，比如从6日（星期日）经过7天是13日，也是星期日。抓住了这样两个不变因素，就可以方便地计算出本月任何一天是星期几。

这种在现实中与人的需求息息相关的真实情境与问题是很多的，需要教师善于观察发现，并且能够与教学内容建立联系。比如在北京、杭州等城市，乘坐地铁出行不仅准时舒适，而且环保，图5是北京地铁1号线线路图。

这样的情境与小学数学课程中的“植树问题”就有紧密的联系。对于有乘坐地铁经验的学生来说，诸如下面的问题都可以成为学生思考讨论的真实问题。

地铁运行一站大约需要多少时间？

地铁在每站大约停多少时间？

从某地到某地共有多少站？

从某地到某地共经过多少站？

从某地到某地需要多少时间？

为了在某个时刻到达目的地，在某地出发去目的地应当几点出发？

再比如，我国许多地区都有过年“包饺子”的习俗，饺子通常会摆放在圆形“盖帘儿”上。（见图6）

在包饺子过程中，人们通常需要知道“是否够吃”，也就是需要迅速知道一个盖帘儿上大约摆放了多少饺子，如果一个一个去数，会比较麻烦。因此就有寻找简便的估算方法的需求。其中实际上蕴含着一个有关圆面积与圆周长之间关系的数学知识，即圆周长的一半与圆半径的乘积等于这个圆的面积。如果用字母r表示圆的半径，圆周长的一半就是，与半径r的乘积为：×r=πr2。由于=2π×，因此这一关系还可以理解为：圆面积等于中间位置的同心圆的周长与圆半径的乘积。（见图7）

估算饺子数量的方法与此相关，在图6第一个图中，中间一圈的饺子数量是25个，总共可以看作是摆放了3圈，因此这个盖帘儿上大约摆放了（25×3=75）个饺子。第二个图也可以用类似方法估算出来。对于小学中低年级学生，关于乘法认识、长方形面积等数学内容，可以用图8中的摆放方式进行探究。

让学生经历真实情境与问题的思考和研究，其目的一方面是让学生感受到数学知识与方法的实际意义，进而诱发学生学习数学的动机。另外对于学生在真实情境中善于发现问题、提出问题、分析问题、解决问题的习惯养成和能力提升，都会有所裨益。真实情境中的问题往往具有开放性，也就是其条件、结论以及过程与方法未必是唯一确定的，因此对于学生综合并且灵活运用知识和方法的能力的逐步提升也会起到积极作用。凡此都需要教师不断开发并积累这样的案例。

参考文献：

[1]郜舒竹，徐春华. 欧拉究竟是怎样解决七桥问题的[J]. 数学通报，2005（1）.

[2]郜舒竹. “探索规律”释义[J]. 课程·教材·教法，2015（1）.

（首都师范大学初等教育学院 100048）