构造平行线 等角图中转

姚璐

在同一平面内，不相交的两条直线称为平行线.平行线是初中平面几何最基本的，也是非常重要的图形.平行线具有强大的转移功能，在解题时如果能根据题目需要构造平行线实现角的转移，那么能使计算证明变得简单、流畅.

构造平行线实现角的转移的依据是：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补.利用平行线的的性质，可以把相关信息转移，实现已知和未知之间的联系，从而解决问题.

下面举例谈谈如何构造平行线实现“角”的转移，供同学们参考.

例 观察图1～图5.

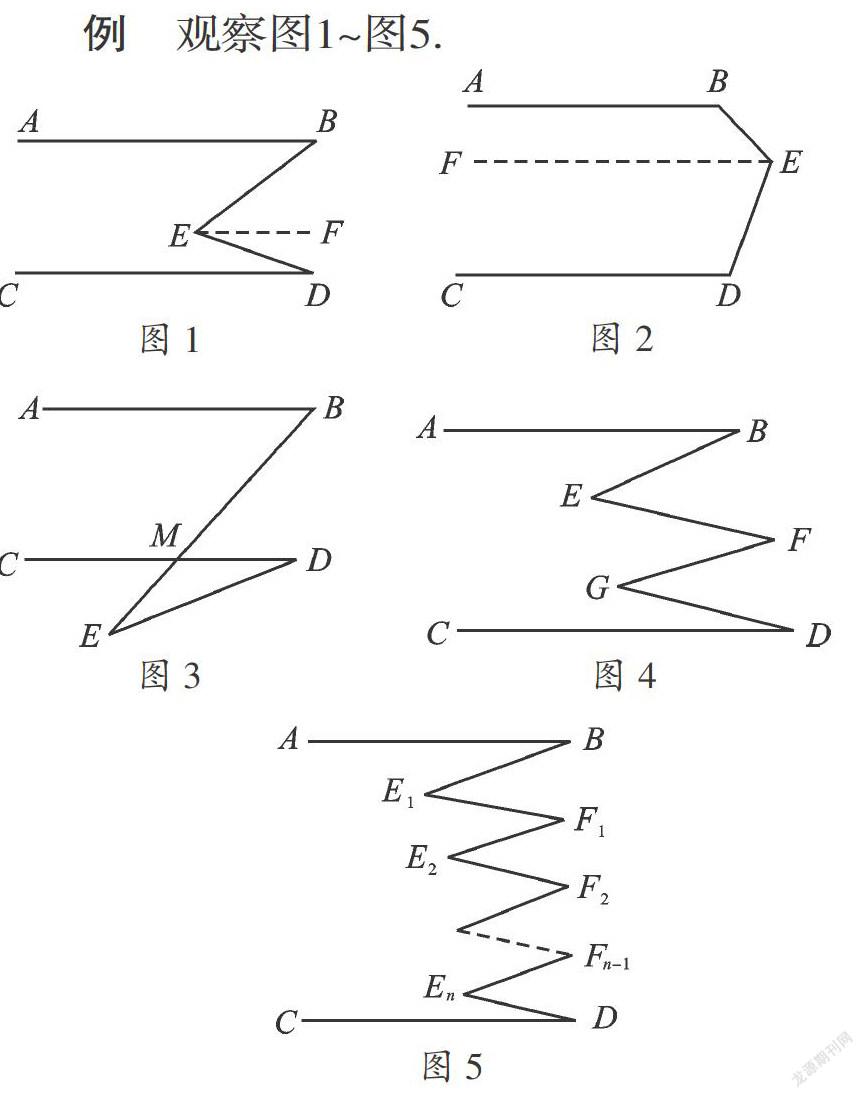
（1）如图1，若AB∥CD，∠B+∠D=∠BED，你能说明为什么吗？

反之，若∠B+∠D=∠BED，直线AB与CD有什么位置关系？请说明理由；

（2）若将点E移至图2所示位置，此时∠B、∠D、∠BED之间有什么关系？请说明理由；

（3）若将E点移至图3所示位置，情况又如何？

（4）如图4，若AB∥CD，∠E+∠G与∠B+∠F+∠D又有何关系？

（5）如图5，若AB∥CD，又得到什么结论？

【分析】要说明（1）的结论成立，难点是如何实现“和”，最直接的方法是将∠B、∠D转移到一起，关键是如何实现角的转移，就请平行线来帮忙吧.若过点E作EF∥AB，则由平行线的性质即可说明；其余几个问题也都可以按照此方法说明.

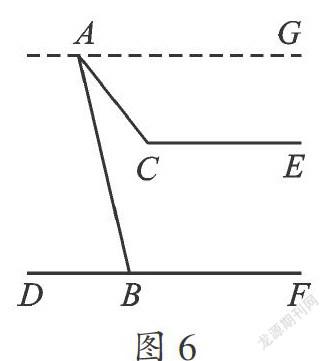
变式2 如图7，已知直线AC∥BD，连接AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分.当动点P落在某个部分时，连接PA、PB，构成∠PAC、∠APB、∠PBD三个角.当动点P在第③部分时，全面探究∠PAC、∠APB、∠PBD之间的关系，并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.（提示：有公共端点的两条重合的射线所组成的角是0°角）

【分析】分点P在射线BA的右侧、在射线BA上、在射线BA的左侧三种情况，过点P作平行线，构造出内错角或同旁内角实现角的转移是解题的关键.

解：①当动点P在射线BA的右侧时（如图8），结论是∠PBD=∠PAC+∠APB.

②当动点P在射线BA上时（如图9），结论是∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°，∠PAC=∠PBD（任写一个即可）.

③当动点P在射线BA的左侧时（如图10），结论是∠PAC=∠APB+∠PBD.