一元一次不等式应用的调查活动方案

潘庆

【活动背景】本次活动是在学习了一元一次不等式的解法、利用一元一次不等式解决实际问题等知识的基础上，经过探索具体情境的数量关系，体会如何进一步利用一元一次不等式来解决实际生活中的较复杂问题.

【课前准备】

1. 调查班级同学父母所在的单位和工作性质，便于选择相关的场所和调查对象

2. 调查所在学校与问题相关的场所，选择适合做调查且组织学生去调查

3. 填写调查表格

你们计划调查的问题＼&＼&你们将选择的调查场所＼&＼&小组成员

【活动过程】

活动一：组织学生进行课外调查

1. 小组分工采访周围熟悉的有关人员或者工厂、农村、商店、农贸市场、银行、邮局等，与相关人员进行交流，收集所需的数据和数量关系.

2. 小组汇报与内部交流

小组的具体分工＼&＼&小组调查的场地与研究对象＼&＼&小组所研究的问题＼&＼&小组利用所得数据处理，构造出能用一元一次不等式解决的问题＼&＼&把相关问题转化为数学问题，列出一元一次不等式＼&＼&解出不等式，并对不等式的解做出解释

活动二：进行全班交流，学生代表汇报活动过程、成果.

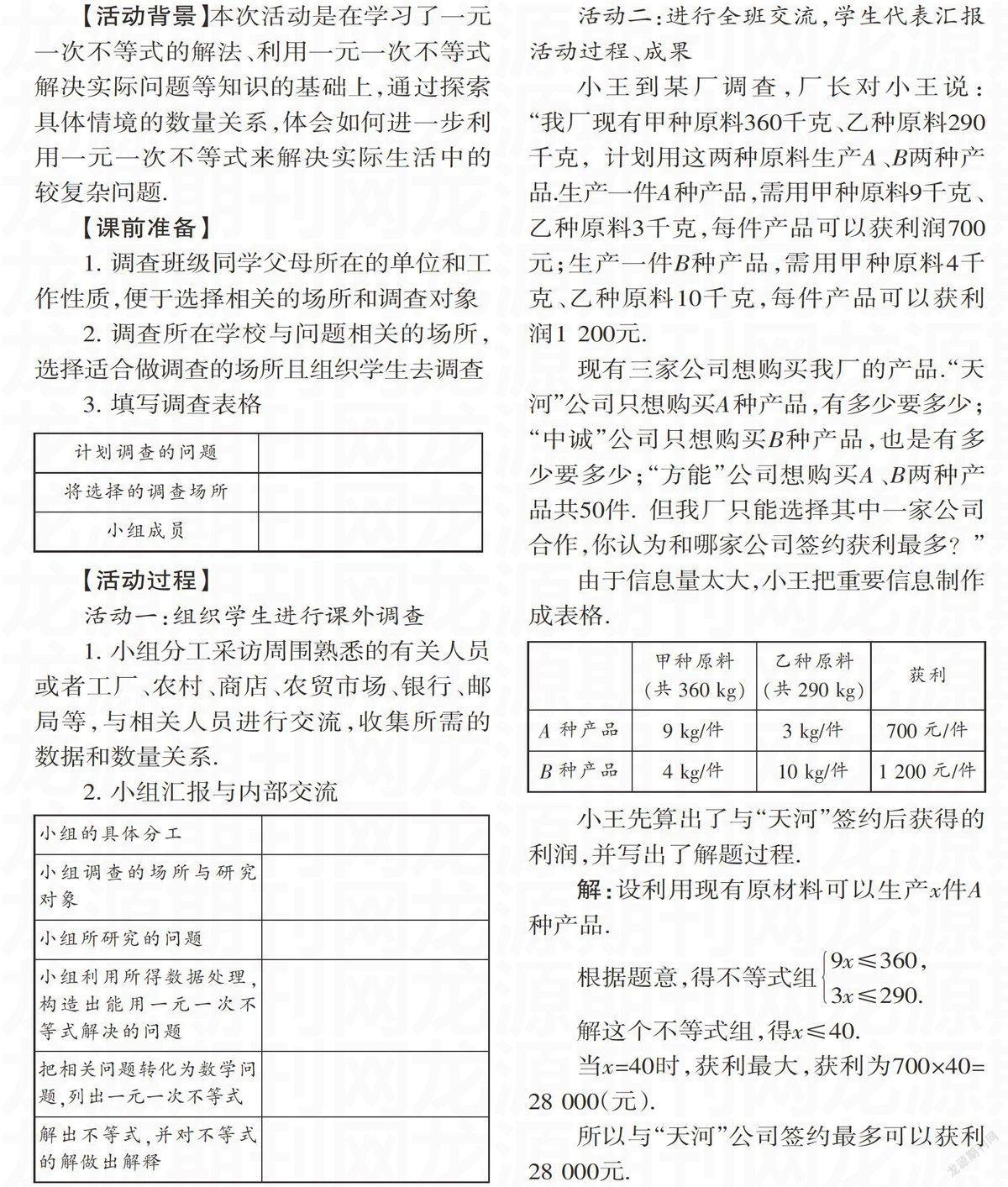
小王到到某厂调查，厂长对小王说：“我厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A、B两种产品.生产一件A种产品，需用甲种原料9千克，乙种原料3千克，每件产品可以获利润700元；生产一件B种产品，需用甲种原料4千克，乙种原料10千克，每件产品可获利润1 200元.

现有三家公司想购买我厂的产品.“天河”公司只想购买A种产品，有多少要多少；“中诚”公司只想购买B种产品，也是有多少要多少；“方能”公司想购买A、B两种产品共50件.但我厂只能选择其中一家公司合作，你认为和哪家公司签约获利最多？”

由于信息量太大，小王把重要信息制作成表格.

＼&甲种原料（共360 kg）＼&乙种原料（共290 kg）＼&获利＼&A种产品＼&9 kg/件＼&＼&3 kg/件＼&700元/件＼&B种产品＼&4 kg/件＼&10 kg/件＼&1 200元/件

小王先算出了与“天河”签约后获得的利润，并写出了解题过程.

解：设利用现有原材料可以生产x件A种产品.

根据题意，得不等式组9x≤360，

3x≤290.

解这个不等式组，得x≤40.

当x=40时，获利最大，获利为700×40=28 000（元）.

所以与“天河”公司签约最多可以获利28 000元.

问题1：请你用如上的方法帮助小王算出与“中诚”公司签约的最大利润吗？

问题2：与“方能”公司签约的情况比较复杂，为了解决这个问题，小王设计了以下的思路：

①设生产A种产品x件，求出x的取值范围，再确定生产B种产品的件数，看看有哪几种生产方案？

②分别计算出这几种方案所获得的利润，哪个方案获得利润最大？你能算出最大利润吗？

问题3：综合以上对三家公司的分析，小王应建议厂长与谁签约？怎样安排生产？

解：（1） 设利用现有原材料可以生产x件B种产品.

根据题意，得不等式组4x≤360，

10x≤290.解得x≤29.

当x=29时，获利为1 200×29=34 800（元）.

所以与“中诚”公司签约最多可以获利34 800元.

（2） ①设生产A种产品x件，则生产B种产品（50-x）件.

根据题意，得不等式组9x+4（50-x）≤360，

3x+10（50-x）≤290.解得30≤x≤32.

因为x为正整数，所以x为30、31、32.所以有三种方案：（a） A种产品30件，B种产品20件；（b） A种产品31件，B种产品19件；（c） A种产品32件，B种产品18件.

②方案（a）获利为700×30+1 200×20=45 000（元）；

方案（b）获利为700×31+1 200×19=44 500（元）；

方案（c）获利为700×32+1 200×18=44 000（元）；

（3） 综合以上的分析，建议厂长与“方能”公司签约，按方案（a）生产.

【活动创新】

第二天，厂长又来找小王，通过市场调研，发现A产品会涨价，用过商谈，“方能”公司愿意按涨价后的价格购买A种产品，但是B种产品的价格不变，厂长想知道是否要调整A、B两种产品的生产数量？小王问厂长A种产品每件会涨价多少元，厂长说目前还不知道.小王通过计算，给了厂长一个完全之策，你知道小王是如何回答厂长的吗？

解：设A产品会涨价a（a>0）元，生产A产品x件，生产A、B两种产品共获利y元.

根据题意，得y=（700+a）x+1 200（50-x），即y=（a-500）x+60 000，

当a=500时，无论x取何值，y=（500-500）x+60 000=60 000，所以方案（a）、（b）、（c）三种方案获利都是一样的；

当a>500时，a-500>0，y随x的增大而增大，所以当x=32时y的值最大，即方案（c）获利最大.

当a<500时，a-500<0，y随x的增大而减小，所以当x=30时y的值最大，即方案（a）获利最大.

给厂长的建议：如果A产品涨价正好是500元，那么不要调整甲、乙两种产品的生产数量；如果A产品涨价高于500元，那么按方案（c）生产，如果A产品涨价低于500元，那么按方案（a）生产.

【活动收获】通过本次活动，你觉得一元一次方程对解决实际问题是否有用？你在调查中遇到来什么困难？你参加本次活动最大的感受与收获是什么？你愿意参加这样的数学活动吗？在活动过程中，你运用了什么数学知识和思想方法？