一节趣味、智慧、高效的复习课

郑艳

初中数学课尤其是复习课，常常给人的感觉是除了做题讲题，还是做题讲题.诚然，数学课是离不开做题的，在设计题目的时候，教师也是煞费苦心的，笔者仅从课堂的趣味性和一贯性上谈谈拙见.

一、案例回顾

第一环节：问题情境引入

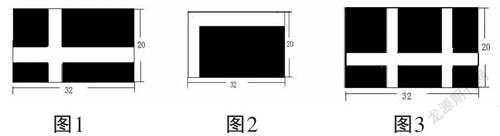
问题1：王老伯承包了一块长方形土地，长32米，宽20米，为了便于灌溉，他在土地上修筑了两条一样宽的水渠（如图1所示），为了使余下部分面积还剩540平方米，水渠的宽度应为多少？

图1                         图2                        图3

变式1：若设计了如图3所示的水渠，则水渠的宽度又为多少？（只列方程，不求解）

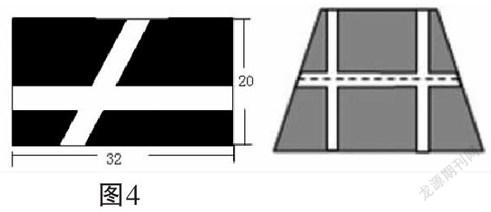
变式2：若把水渠由直线改为斜线（如图4所示），那么水渠的宽度又为多少？（直接说出答案）

图4

变式3：要设计一个等腰梯形花坛，花坛上底长100m，下底长180m，上下底相距80m，在两腰中点连线处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等，甬道的面积是梯形面积的六分之一，甬道的宽应是多少？（只列方程）

第二环节：变式训练

问题2：王老伯在该土地上种植芹菜，喜获丰收.经计算，芹菜成本2元/千克，若以3元/千克的价格出售，每天可售出200千克，为了促销，王老伯决定降价销售.经调查发现，这种芹菜每降价0.1元/千克，每天可多售出40千克.另外，每天的房租等固定成本需要24元.王老伯要想每天盈利200元，并想使芹菜尽快销售出去，应将每千克芹菜的售价降低多少钱？

问题3：王老伯算了算，2012年种植芹菜共获利2160元，他记得自己2010年种植芹菜时只获利1500元，若从2010年到2012年，每年获利的年增长率相同.

（1）王老伯2011年的获利为多少？

（2）若获利的年增长率继续保持不变，预计2013年王老伯将获利多少？

第三环节：巩固提高

采用分组竞赛的形式，解决相关针对性的练习题.

奋进组：

为落实国务院房地产调控政策，使“居者有其屋”，某市加快了廉租房的建设力度.2011年市政府共投资2亿元人民币建设了廉租房8万平方米，预计到2012年底三年累计投资9.5亿元人民币建设廉租房，若在这两年内每年投资的增长率相同.

（1）求每年市政府投资的增长率;

（2）若这两年内的建设成本不变，求到2012年底共建设了多少万平方米廉租房？

宏志组：

某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的售价与销售量有如下关系：若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售出1部，所有售出的汽车的进价均降低0.1万元/部;月底厂家根据销售量一次性返利给销售公司，销售10部以内（含10部），每部返利0.5万元;销售量在10部以上，每部返利1万元.

（1）若该公司当月售出3部汽车，则每部汽车的进价为？摇？摇？摇？摇万元.

（2）如果汽车的售价为28万元/部，该公司计划当月盈利12万元，那么需要售出多少部汽车？（盈利=销售利润+返利）

精英组：“？”的思考

下框中是小明对一道题目的解答及老师的批注：

题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前面内墙保留3m宽的空地，其他三面内墙各保留1m宽的通道。当温室的长与宽各是多少时，矩形蔬菜种植区域的面积是288m ？

解：设矩形蔬菜种植区域的宽为x m，则长为2x  m.

根据题意，得x·2x=288

所以温室的长为2×12+3+1=28（m），宽为12+1+1=14（m）

答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288

小明发现他解答的结果是正确的，但是老师却在他的解答中划了一条横线，并打了一个“？”.

结果为何正确呢？

（1）请指出小明解答中存在的问题，并补充缺少的过程.

变化一下会怎样？

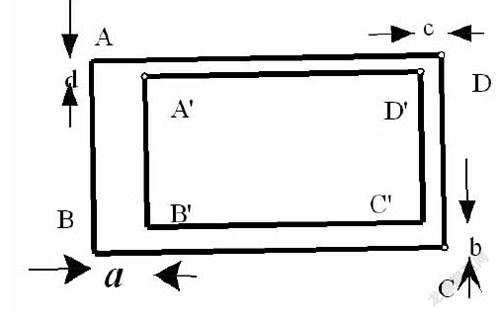
（2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB=2：1.设AB与A′B′，BC与B′C′，CD与C′D′，DA与D′A′之间的距离分别为要使矩形A′B′C′D′∽矩形ABCD，应满足什么条件？请说明理由.

二、设计意图与想法

本节课的主题是巩固发展学生的应用意识，这是方程教学的重要任务.在前面的新课中，已经选用了大量的实际问题，通过列方程解决问题，并且在问题解决过程中促进了学生分析问题、解决问题的意识和能力的提高，以及方程观的初步形成.

这节课从调动学生的积极性入手，努力挖掘学生的主动性和合作性，增强学生克服困难的决心.为此，本节课在体现新课程理念方面做了大胆的尝试.整节课以王老伯的故事为主线，一边讲故事，一边解决问题，让学生置身于故事之中，用故事勾起学生学习知识的内驱力，使学生更愿学、更乐学.故事中的王老伯向学生求助了很多问题，学生对王老伯而言是专家、是能者，更能激起学生解决问题的欲望，让学生的学习更积极、更主动，在自觉和不自觉中牢固地掌握数学知识解决一元二次方程应用中的3类重点问题（面积问题、经济问题、增长率问题）.

在问题情境教学中，尝试运用了如下几种方法：问题一是面积问题，问题一的学习主要采取教师引导式教学，通过师生共同解决问题，使学生更熟练掌握列一元二次方程解决实际问题的一般步骤.以变式训练的形式对问题进行深入研究，使问题具有层次性和内在的联系，并揭示了解决同类问题的通解和通法，使问题更具一般性，这样的设计能使学生较自然地参与到问题解决的过程中.问题二是经济问题，题目在课本例题的基础上略有拔高，课前预设学生审题会有一定的困难，所以安排学生先独立审题，再以小组说题这样一个形式帮助学生审题，上黑板板演的学生是一个中等偏下的学生，尽管知道她完成情况不是很好，但还是想鼓励一下她，总体完成情况较理想.问题三是增长率问题，难度不大，所以采用了独立完成小组批改这样的形式学习，目的是想充分调动学生学习的积极主动性.

经过三个问题的研究学习，考虑学生可能会出现思维疲劳，所以想到通过小组竞赛的形式调动学生思维的活跃性，分层完成各自问题，三个问题均源于本课例题，也高于例题.最后分层交流，分层展示.

三、几点思考

1.跳出模式，还原习题课的教学价值

习题课的价值在于使学生达到对知识的深层次理解，让学生学会解决问题、掌握知识方法、领悟数学思想，这是习题课教学的核心目标.这节复习课有别于传统的复习课，它以帮王老伯解决问题的这一任务贯穿整堂课，三个问题层层深入，复习了课本所要复习的三个典型问题.练习题的设计是本节课的亮点，分层设计能让不同层次的学生得到不同层次的训练.

2.重视通性通法教学，实现能力的有效提高

在问题1中，设计了三个变式训练题，这种题型是中考常见考题，通过变换图形，将数学问题的本质从复杂的图形中剥离出来，从而使学生达到做一题会一类的目的，三题训练完的总结很必要.问题2以学生先独立审题，再小组说题这样一个形式帮助学生审题，为习题2埋下伏笔.通过策略的优化，不仅充分挖掘学生的潜能，而且使学生的思维能力不断得到提高.

3.重视追问，突出思维的拓展与延伸

本节课教师始终围绕主线不变，通过巧妙的问题设计，不断追问，鼓励学生观察问题、发现问题，引导学生展现思考过程和解题方法.每个追问又紧扣问题实质.如问题1中，学生解决图1后，教师追问：“你是怎么想的？”这样既帮助学生理清了解题思路，又为下面的变式训练提供了基本解题方法，为下面问题的解决做好了铺垫，同时培养了学生的口头表达能力.

4.分层教学，培养学生的合作交流能力

教师在教学过程中，特别重视师生之间、生生之间的互动生成.教学过程中不仅让学生比较黑板上学生的解答，而且让板演的学生说明解答的理由和过程，还让学生互相讲解.互相批改.与此同时，教师还变换角度进行追问，如用“还有没有不同的表达方式”等促进学生的思考，并及时进行生成性总结.这样的互动，学生不但知其然，而且知其所以然，进而领悟其中的数学思想方法，积累数学活动经验.练习的分层设计更体现了以学生为主体，充分尊重了主体之间的差异，在独立学习的基础上进行合作学习，提高了学生的合作交流能力.

5.有待完善之处

（1）训练量的把握

本节复习课，课堂容量很大，三种题型全部复习到位，问题1的变式训练就有3题，练习题中的1、2两题都高于例题，还要分类讨论，对于这些题目，学生能否真正理解到位？

（2）时间的把握

学生自主探究的时间，合作小组讨论交流的时间，教师与学生互动的时间，怎样分配才算合适？本节课由于在生生互动中花费时间较多，导致后面的练习题展示显得较仓促.由此产生如下问题：“互动中出现的新问题究竟哪些需要当场解决，哪些可以留在最后？”

（3）分层合作的时机的把握

生生之间的合作是不是一定要教师统一安排，还是可以由组内同学自己组织？这对我们是一个值得思考的问题.统一组织，有利于课堂教学内容的推进，但会导致一些问题流于形式，讨论不到位，或者假谈论.而如果不统一组织安排，全班交流又该放在哪个环节？训练题的分层设计，是设计成三种题型各一题，还是一种题型安排三题更能体现分层的价值？

参考文献：

[1]潘晓梅，张良江.数学联想显方法经历过程孕思想.中学数学教学参考：中旬，2013（5）：23-26.