关于“相量法”的一种讲授方法

蓝屹群

摘 要： 本文用比较分析法，对大学电工学“相量法”一节的讲授方式进行了探索，目的是通过该方法，凸显“相量图”在解决正弦交流电问题时所具有的天然优势，从而便于学生深刻理解、掌握和应用。

关键词： 正弦交流电 相量法 代数法 复数法

一、引言

在大学本（专）科电工电子课程教学中，“正弦交流电”是极其重要的一个环节，因为在生产和生活中所使用的一般都是正弦交流电。从常规的教学进程看，教师介绍完正弦交流电的基本特性参数（如周期、频率、初相位、相位差、振幅、有效值等），通常接着要讲解正弦量的三种表示方法，即波形图法、代数式法及最重要的——相量法（旋转矢量法）。对于前二者，其表达正弦量时的优点是显而易见的，如波形图形象直观，容易看出信号的变化趋势；代数式容易看出正弦量的三要素，关于这些学生都是容易理解和接受的。然而对于“相量法”，以笔者的教学体会看，虽然经过操练，学生能正确画出某个正弦量的对应相量图，但对用相量法表示正弦量在解决问题时的独特优势，学生往往不能很好地领会，即知其然而不知其所以然。为此，笔者在教学中作了如下设计。

二、教学步骤

首先笔者先举例介绍一下相量图的画法。

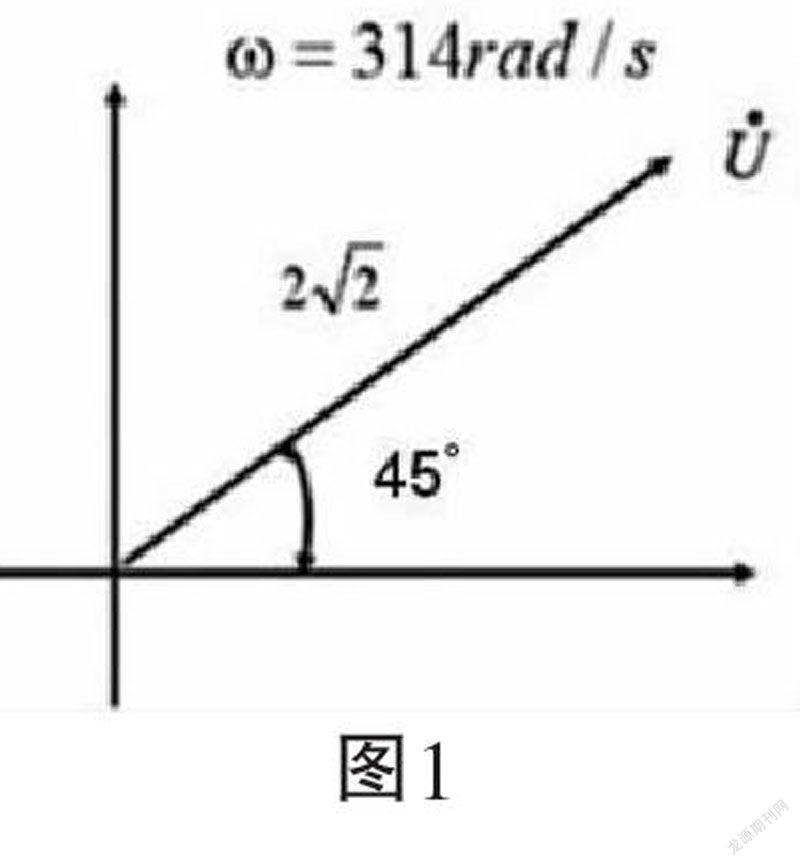
如现有一正弦电压，其表达式为u=2sin（314t+45°）V，则该信号的相量图为直角坐标系中的一个相量，该相量的长度即为正弦量的振幅2，其与横轴的夹角即为正弦量之初相位（如图1所示）。

接下来，为熟练起见，教师可随意写出一些不同的正弦量表达式，令学生模仿画出对应相量图。一般来说，由于问题不难，学生都能做得快又好。但在学会画法以后，学生对相量图的内涵和解决问题的优势却往往不甚理解。换句话说，学生不明白为何要将正弦信号表示为这样一个带箭头的相量。为说明此问题，笔者举出下面一道例题（如图2所示）：

该电路为一R、L电路，为简单起见，已知电感感抗X=1Ω，R=1Ω，且i=1·sinωt（A），问⑴总电路端电压为何种电压？（直流？交流？其他？）（2）端电压最大值为多少？

假设学生已经学习过单一参数交流电路（纯电阻/电感/电容电路），一般而言，他们能很快答出两个元件上电压皆为交流电压，甚至能够给出各元件上电压的表达式（如下）：

uR=Usinωt=IRsinωt=1·1·sinωt=sinωt

uL=Usin（ωt+90°）=lXsin（ωt+90°）=1·1·sin（ωt+90°）=sin（ωt+90°）

此时显然，根据KVL，电路端电压表达式

u=uR+uL=sinωt+sin（ωt+90°）

不妨让学生直接根据表达式，思考其最大值为多少？每次笔者提出问题后，有些学生会想当然指出，表达式第1项和第2项的最大值都为1，故其和式的最大值为2。该结论笔者姑且存之，另一方面，笔者又在黑板上作了如下演算：利用三角学中的和差化积公式sinA+sinB=2sin（）cos（），此时令α=ωt，β=ωt+90°，则

u=sinωt+sin（ωt+90°）=2sin（）cos（），

=2sin（ωt+45°）·=sin（ωt+45°）

由以上计算，可以自然地得出，此时端电压u仍然是一个正弦量，且其最大值为，而非先前学生所猜测的2。教师可因势利导画出的波形图（如图3所示），指出，从波形图来看，由于（初）相位不同，sinωt和sin（ωt+90°）并非同时达到最大值，故的最大值就不可能为2（顺便复习初相位的作用）。接下来，可让学生用相量法在黑板上画出uR，UL的相量图，如图4所示，既然端电压u=uR+uL，则在相量图上，端电压u所对应相量自然为U，U根据平行四边形法则作出的合相量。既然一个正弦量可表示为一个带箭头的相量，反之一个相量亦表征一个正弦量，故端电压必是一个正弦量。故可设u=Usin（ω′t+φ），从图上可以非常直观地看出，U即为u所对应相量的长度，u的初相位即为与横轴的夹角45°（显然△OBC为等腰直角三角形），至于u的角频率ω′，此时教师应提醒学生注意，并非静态相量，而是以角速度ω做逆时针匀速转动，则它们的合相量自然以ω做同步转动，即ω′=ω，故立刻得到，端电压u=sin（ωt+45°），其结果与代数法的结论完全相同，且求解速度较快（从相量图上，教师可顺便指出，对于不同频率的正弦量的合成，由于图中各分相量与合相量并不能同步旋转，故相量法只能用于同频率的信号合成。）。

为深化结论，教师还可将原题的题设条件稍作改动，比如令原电路中电感感抗X=2Ω，则u=sinωt+2sin（ωt+90°），该表达式从代数法来讲并无现成公式可用，但用从相量图依然可直接得出其最值为，频率仍然为ω，从几何上容易看出其初相位为arctg2，说明用相量图求解交流电的问题在方法上具有普适性。

此外，如学生已学过复数，亦可将uR，uL看做复数，此问题可用复数法求解，过程如下：

=+=1∠0°+1∠90°=1（cos0°+jsin0°）+1（cos90°+jsin90°）

=1+j=∠45°

该过程同样可以说明，u的振幅（最大值）为，初相位（即复数的幅角45°），然而由于该计算过程需将信号按欧拉公式展开，并将实、虚部合并，较之相量图分析问题，步骤稍显繁琐，效率不高。可以想象，对于情况更复杂的电路（如RLC电路），无论是代数法还是复数法均远不如相量图法简洁高效。

三、结语

笔者对同一道题用不同方法进行了剖析，并且比较了几种方法的优缺点。从实际教学效果看，通过这些例子，学生对相量法的优势有了比较深入的了解，碰到更复杂的问题也能够自觉使用该方法求解，避免“知其然而不知其所以然”。推而广之，在教学中遇到难点，教师如从多方引导、比较，从多角度分析问题，相信学生对知识点的掌握就能更透彻扎实。

参考文献：

[1]秦曾煌，编.电工学.上册.北京：高等教育出版社，2004.1.

[2]王照清，编.维修电工.初级.北京：中国劳动社会保障出版社，2005.3.