一元一次不等式组教学设计

本文是2015年5月22日作者在北京市某中学执教的一节示范课的教学设计.现不揣浅陋，请大家斧正.

教学目标

1.了解一元一次不等式组的概念，理解一元一次不等式组的解集的意义.

2.会解简单的一元一次不等式组，规范解一元一次不等式组的步骤.

3.经历知识的拓展过程，感受学习一元一次不等式组的必要性；

4.渗透数形结合的思想方法，感受类比与化归的思想，训练总结、归纳、抽象、概括的能力.

教学重点、难点

重点：一元一次不等式组的有关概念、解法的获得过程.

难点：解一元一次不等式组的规范表达.

教学过程设计

（请同学们都合上课本，我们在数学课上需要通过真正（真实）的独立思考来获得知识、方法、经验.）

同学们前几节课学习了不等式的有关内容，今天我们继续学习：（板书课题）

9.3一元一次不等式组

一、设计问题，创设情境

问题1 今天北京市朝阳区32℃～18℃，即最低气温是18℃，最高温度是32℃，请同学们回答，如果在今天的某一时刻的温度设为t℃，那么t应当满足什么样的不等关系？

（稍停2秒）——知道的同学请举手（或谁想回答），然后指定一名学生回答.

学生口答：t≥18且t≤32.

问题2 昨天老师自己开车从山东省滨州市来北京市，全程大于340km而小于360km，假设老师的车速平均每小时100km，并且上午8：00出发要求中午12：00之前赶到，那么老师到达北京所用时间t应当满足什么样的不等关系？

（给学生30秒时间思考，然后让学生主动回答.回答后，请他说一说自己的思考过程（理由），并问同学们有没有不同意见，也说说你的理由.——追问为什么？有无其他意见、想法）

根据（人教版七年级（上册）第54页）：路程=速度×时间，得

100t>340且100t<360且t<4.

问题3 请类比已学的“方程组”（课本P88）、“二元一次方程组”（课本P88）、“二元一次方程组的解”（课本P89）、“不等式的解”（课本P114）、“不等式的解集”、“解不等式”（课本P115）等概念，给出（猜测）“不等式组”、“一元一次不等式组”、“不等式组的解”、“不等式组的解集”、“解不等式组”等概念.

注意 本文中所指的“课本”均是指人教版七年级（下册）（数学）.下同.

（下面给同学们5分钟的时间完成问题3，要求：一是不能看本节内容；二是必须先独立思考，尽量独立完成，确有困难时，再与同学交流、讨论.5分钟后，个人或小组代表汇报成果.）

二、信息交流，揭示规律

（5分钟后，个人或小组代表汇报成果.并问同学们有没有不同意见，也说说你的理由.——追问为什么？有无其他意见、想法）

结论：

1.若t同时满足不等式

100t>340且100t<360且t<4.（或t≥18且t≤32.）

把这些不等式合在一起，写成

就组成了一个不等式组.这个不等式组中有一个未知数（一元），未知数的次数都是1（一次），（或这个不等式组中的不等式都是一元一次不等式），（或由若干个一元一次不等式组成的不等式组），像这样的不等式组叫做一元一次不等式组.

注意 （1）一个不等式组中，最少有2个不等式.——要不然就不用“合在一起了“；

（2）“合在一起“的含义是，同时成立；

（3）一般未知数习惯上用x来表示，所以上述不等式组中的t习惯上用x代替.

2.一般地，不等式组中的所有不等式的公共解，叫做不等式组的解.

3.不等式组的所有的解，组成这个不等式组的解集.换句话说，一般地，不等式组中所有不等式的解集的公共部分，叫做这个不等式组的解集.

4.求不等式组的解集的过程叫做解不等式组.

下面给同学们1分钟的时间，请与课本上的定义比较，看看有无不同.并要求默记上面的5个概念.

为什么要求同学们记忆上面的5个概念？因为下面就要解一元一次不等式组，结果你还不知道啥叫解一元一次不等式组，那怎么解？反过来，若你知道啥叫解一元一次不等式组，那就是求出不等式组的解集，那就要先求出不等式组中各个不等式的解集，然后再取其公共部分即可.这不是连解不等式组的程序或步骤都有了吗！第一步：解不等式组中的各个不等式，求出各个不等式的解集；第二步，取这些解集的公共部分，即得不等式组的解集.所以，数学学习同样需要记忆！

三、运用规律，解决问题

把前面两个不等式组中的t换成我们习惯的x，看看具体怎样求解一个一元一次不等式组：

（以上解答就是规范解答.但是由于不等式的解集可以在数轴上表示出来，有时还可能更直观、更清楚、更方便的让我们找出不等式组的解集，所以我们利用数轴上的表示，看看我们上面的解答是否正确.——但一定要注意：这不是规定动作.即可以只在自己的脑子里想一下或写在练习本上或草稿纸上.）

把不等式组中的所有不等式的解集在数轴上表示出来（如图1）.

四、变练演编，深化提高

问题4 解一元一次不等式组的步骤是什么？

问题4的答案之一：（讨论交流后得出，）解一元一次不等式组有以下几步：

（1）求出不等式组中的各个不等式的解集；

（2）取公共部分，写出不等式组的解集.（借助数轴找出各解集的公共部分（可以不写上，只在脑中想、练习本、草稿纸上画））.

注意 若各个不等式的解集没有公共部分，则称不等式组无解.

归纳：解一元一次不等式组时，一般地，既可以整体等价解答（如，例1（2）的解法1），也可以先求出其中各个不等式的解集，再求出这些解集的公共部分（如，例1（2）的解法2）.利用数轴可以直观地表示不等式组的解集.

问题5 请同学们自己编几道你喜欢的解一元一次不等式组的题目，并与同桌交换解答.最后每个小组选出组内最喜欢的两道题目，写到黑板上，然后每个小组再派出代表，选你喜欢的其它某个小组的题目，上台解答.

（注意 最后一定要问：你是怎样编出这几道题目的？告诉学生，若能直接到课本上的一元一次不等式处找几个你喜欢的一元一次不等式，然后，把两个及两个以上的一元一次不等式合在一起，不就完成编写任务了吗？而且不等式组的解集也在你的掌握之中，想有解还是无解；有解时，想让解在“中间”还是“两边”等等.几乎可以随心所欲.）

五、反思小结，观点提炼

请同学们想一想：这节课你收获了哪些知识？是怎样得到这些知识的？在获得这些知识的过程中都用到了哪些思想、方法？你有哪些感悟？

（不等式组和一元一次不等式组的概念、解、解集、解不等式组等；是用类比的方法得到的；类比的思想、转化的思想、数形结合的思想；感悟：数学知识之间是有联系的，只要抓住了或找到了这个联系，实质上一节课并没有多少新内容（知识、方法、思想等），学好当前的，才能学好以后的，基础很重要！数学学习同样需要记忆！）

（若时间还余3～5分钟，则让学生回忆、整理本节内容，并提出自己的疑惑、经验、或独到见解.若时间多于5分钟，则可安排最后面的“七、当堂达标，及时反馈”）

六、布置作业，及时巩固

必做题 课本第130页习题9.3的1，2，3；

选做题 课本第130页习题9.3的4，5，6.

同学们！数学学习要想学得轻松，那就要善于抓住知识之间的联系，打好基础，善于记忆！数学学习同样需要记忆！只要抓住了知识之间的联系，就能类比着学，对比着学，不仅大大减轻了记忆负担，而且记得好、记得牢，进而觉得每节课都没有多少新内容，无非就是旧知识的自然生长，旧方法的新运用而已.愿同学们高高兴兴上好每一节课，数学学习越来越轻松！有趣！好玩！

七、当堂达标，及时反馈

解下列不等式组，并把解集在数轴上表示出来.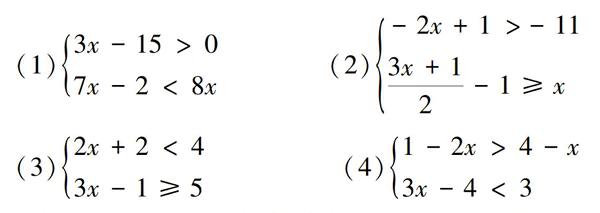

（由四名学生板演，其他学生在下面练习，最后师生共同规范订正.解答从略.）

八、回顾与反思

1.采用“合上书”与“换一个”的策略，所以本设计中的引入和例题均没有直接运用课本上的问题和例题，而是根据当时的实际情况自编了问题1、2和例1，其目的就是使学生在数学课上需要通过真正的认真、积极、踏实、真实的独立思考来获得知识、方法、经验、解法，即使有时需要合作学习，但也是在首先独立思考的基础上，这样虽然有时不顺利、磕磕绊绊、反反复复，但可以避免假思考、假顺畅、假热闹、假繁荣，使学生真动脑、真思考、真参与、真讨论，学有所获、学有所成，学会思考、学会思维、学会分析、学会学习、学会独立解决问题.

2.根据学生原有的知识结构进行教学，即找准知识的生长点是上好一节课的前提，也是减负增效的有效措施.这样会使学生觉得新知识就是旧知识的自然生长，新方法就是旧方法在新情境中的新运用；因此，本设计通过问题3让学生类比之前学过的“方程组”和“不等式”的有关概念自得（猜测）“不等式组”的有关概念，不仅打破了课本上“一元一次不等式组”的概念仅限于“把两个不等式合起来”的说法的限制（课本第130页第5题就是由三个不等式组成的方程组问题），而且还得出了课本上没有的“不等式组”、“不等式组的解”的概念.

3.设置问题5，请同学们自己编几道你喜欢的解一元一次不等式组的题目.不仅丰富了课堂素材，而且提高了学生的合作意识和参与的积极性，并考查了学生对“一元一次不等式组”概念的理解.尤其是教师在学生编完、练完之后的一问：你是怎样编出这几道题目的？一答：告诉学生，若能直接到课本上刚刚学过的一元一次不等式处找几个你喜欢的一元一次不等式，然后，把两个及两个以上的一元一次不等式合在一起，不就完成编写任务了吗？而且不等式组的解集也在你的掌握之中，想有解还是无解；有解时，想让解在“中间”还是“两边”等等.几乎可以随心所欲.不仅把握了不等式组的实质、学会了编题，而且使教为主导，学为主体得到了有效落实.

4.本设计的小结环节，不是简单的教师罗列，或当前最为时髦的让学生谈谈收获，而是明确要求学生从“收获了什么”、“怎样获得的”、“用到了什么”、“有何感悟”等四个方面进行反思、总结，这样可以进一步提高课堂教学效益.

九、一点感想

当前的数学课堂教学，由于所谓的“学案教学”的泛滥（相当于看书填空）和教师把问题分的很细、很小（相当于教师嚼碎了喂给学生吃），然后，就是例题讲解、课堂练习，完完全全把新授课上成了习题课.长此以往使得现在的学生不愿意思考，也不会思考；不愿意动脑，也不会动脑；不愿意动手，也不会动手（写）；不愿意读课本，也不会读课本；不愿意总结概括，也不会总结概括；对问题的理解浮于表面，根本就是稀里糊涂、顺势而下，甚至于连条件与结论都不真正清楚就能解题，更不用说问为什么，表面的活跃，课上的顺利，是基于没有思考的实际，遇到真正需要思考的问题就畏惧、就抗拒，甚至于直言不讳的要求老师讲解.这样的教学现实，只能是题海战术、机械训练、考试机器，那么要实现数学教学就是数学思维的教学的目标就是空谈，培养学生提出问题、解决问题的能力也就是空想，培养学生的创新意识和创新能力更是幻想、奢望.我们的中学数学教学的目标何在？质量何在？效益何在？希望何在？作为一名工作在教育教研一线的工作者在此强烈呼吁，为了祖国的未来，为了培养学生的思维能力、创新能力等，数学教学要返璞归真，要打假，要求真务实！课堂上要真正（真实）学（教）读教材、学（教）总结、学（教）概括、学（教）表达、学（教）思考、学（教）思维、学（教）逻辑、学（教）推理、学（教）道理、学（教）方法、学（教）思想、学（教）发现、学（教）提问、学（教）创新！使课堂教学回归真实、扎实、踏实、朴实、平实.

参考文献

[1] 王文清.怎样的数学课才算好课 怎样才能上好数学课[J].中学数学杂志，2008（8）；1—7.

作者简介 王文清，男，1963年3月生，中学高级教师，省特级教师，省优秀教师，省教学能手，滨州市有突出贡献的专业技术人员.出版专著2本，主编或参编教学辅导用书80余本；在《数学通报》、《中学数学杂志》等省级以上专业杂志发表论文110余篇，其中，有12篇被中国人民大学复印报刊资料《中学数学教与学》全文转载；主持省教育规划课题4项；有2项成果获山东省省级教学成果奖.多次执教省、市级公开课，多次到省内外给师生作专题报告或执教示范课.