充分体现课标理念促进学生全面发展

李树臣

《义务教育数学课程标准（2011年版）》（以下简称《课标（2011年版）》是指导义务教育数学教科书编写的“纲领性文件”.本文中笔者以青岛版初中数学教科书（七—九年级）为例，将教材编写的主要原则进行归纳介绍.

1 突出核心概念，体现课程内容的核心

《课标（2011年版）》指出“在数学课程中，应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想.为了适应时代发展对人才培养的需要，数学课程还要特别注重发展学生的应用意识和创新意识[1]”.这十个核心概念是学生应具备的基本数学素养，理应成为教科书的核心内容，教科书在整体设计时应以这些核心概念为主线.

例如，数感主要是对于数与数量、数量关系、运算结果的估计等方面的感悟.在第三学段，学生对于数的认识共经历过两次扩充.第一次是从第二学段对算术数的认识以及对负数的初步认识扩充到有理数；第二次是由有理数扩充到实数.青岛版教科书一方面从具体的生活中选取案例，让学生理解现实生活中的有理数与实数的意义，另一方面还通过具体问题让学生感受新数的产生是数学内部自身发展的需要.例如，在学习有理数后，让学生通过有理数的运算，感受有理数运算与算术数运算的联系和区别；在学习无理数时，让学生通过估算无理数的近似值，感受无理数是确实存在的，以及无理数与有理数的联系和区别；在学习一元一次方程、一元二次方程时，让学生通过估算方程的根，感受数学中有限与无限的关系和逐次逼近的思想方法.

再如，推理能力包括合情推理能力和演绎推理能力.《课标（2011年版）》将义务教育阶段的课程内容分为“数与代数”“图形与几何”“统计与概率”“综合与实践”四个部分.每个部分的许多内容中都伴有分析、判断和推理的过程，这为学生合情推理能力的培养与发展提供了机会.青岛版教科书在以上四个部分内容中，都结合具体的课程内容，精心设计了观察、操作、分析、归纳、类比、猜测等活动，这些活动对于培养学生的合情推理能力，提高学生的数学素养都具有积极的意义.

2 注重数学实质，突出内容之间的相互关联

《课标（2011年版）》指出“教材编写应体现整体性[1]”，“教材的整体设计要呈现不同数学知识之间的关联.一些数学知识之间存在逻辑顺序，教材编写应有利于学生感悟这种顺序[1]”.很多数学知识之间都存在着实质性的联系，这些联系既体现在前面所述的四个部分的内部，也体现在四个部分之间.在编写教材时，一定要把数学本身固有的这种实质性联系突出出来.

例如，为突出知识之间的本质联系，还原数学的本来面貌，青岛版教科书将传统教材中“勾股定理”和“数的开方”中的有关内容“整合”为一章，取名为“实数”.

虽然勾股定理和实数分属于“图形与几何”和“数与代数”两个部分，但从科学发展史来看，这二者却有着密切的关联，在本质上是并存发展的.如常见的无理数2，3，5等都是伴随着勾股定理的发现而被发现的，因此，我们说无理数是保证勾股定理对于边长是任意正数的直角三角形都成立的必要条件，而勾股定理使得平方根有了明确直观的几何解释.

把“勾股定理”和“数的开方”中的相关内容整合为一章，不仅仅解决了究竟把勾股定理安排在实数前面还是后面的矛盾，最为关键的是只有把二者合为一体，才能尊重数学史实，揭示出它们原本固有的这种相互“交融”的实质性联系，从而体现出数学的整体性和文化价值，突出了数形结合的思想，把实数（勾股定理）“还原”到其应在的“位置”之中，回归到人类发现勾股定理和实数的历史之中.

本章之后将在实数范围内讨论一元一次不等式、二次根式、一次函数.这种统筹安排、整体设计的方式有利于学生逐步掌握当数域扩充后数学研究的规律和方法，加深了学生对数学本质的理解与感受.同时，这种设计更加印证了人类对数的认识是在生产、生活和数学自身矛盾的发展过程中不断加深和完善的事实.

3 体现知识的形成过程，反映知识的应用过程

《课标（2011年版）》提出“课程内容的组织要重视过程，处理好过程与结果的关系[1]”.“教材内容的呈现要体现数学知识的整体性，体现重要的数学知识和方法的产生、发展和应用过程；应引导学生进行自主探索与合作交流，并关注对学生人文精神的培养[1]”.例如，青岛版教科书为了体现数学知识的形成过程，用“观察与思考”、“交流与发现”、“实验与探究”三个栏目中的问题引导学生进行观察、实验、猜测、计算、交流、发现、推理、验证等数学活动，在经历这些活动的过程中获得数学基础知识，形成数学基本技能，感悟数学基本思想，积累基本的数学活动经验.

例如，七年级上册共60课时，有这样的栏目44个，其中交流与发现23个，观察与思考14个，实验与探究7个；下册共61课时，这样的栏目57个，其中交流与发现23个，观察与思考24个，实验与探究10个[2].

这些栏目的主要作用是：（1）帮助学生理解数学；（2）帮助学生学习新的数学知识；（3）培养和发展学生的数学能力；（4）引导学生积累数学活动经验；（5）帮助学生理解数学知识之间的联系；（6）引导学生进行实验操作活动.

事实上，这些栏目的设置，一方面反映了数学的本质，体现出“问题情境—建立模型—求解验证”的编排模式.另一方面便于处理教材中的相关内容、使得段落之间的衔接自然，便于教师和学生在教学中使用.

案例1 轴对称图形的形成过程[3].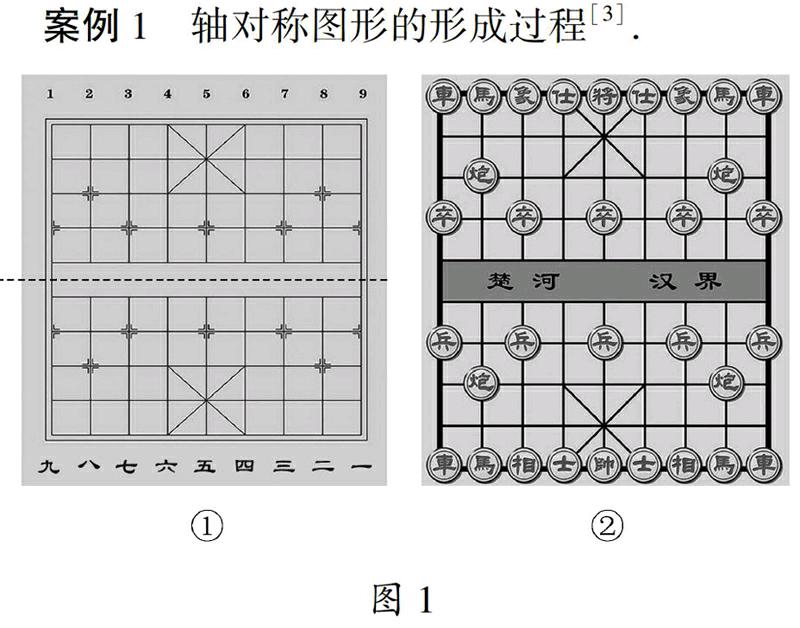

为了让学生经历轴对称图形概念的形成过程，青岛版教科书用“观察与思考”栏目引导学生思考与探究如下的问题：

（1）图1①是一幅中国象棋棋盘，如果把棋盘沿着中间的虚线对折，棋盘的上下两部分将会怎样？