极限求解方法研究*

景慧丽

(第二炮兵工程大学)

0 引言

极限是《高等数学》课程中最重要的概念之一.极限思想贯穿整个教材，它是微积分的灵魂.《高等数学》课程中的很多概念都是由极限来定义的，例如，导数、定积分、反常积分、偏导数、重积分、曲线积分、曲面积分等.因此，理解极限思想的内涵和掌握求极限的方法是学习这门课程的基本要求.但是，笔者在教学过程中发现大部分学员往往对求极限这一问题感到束手无策、无从下手，这一方面是因为求极限的题目类型比较多，求解方法也是因题而异，变化多端.另一方面是因为几乎所有的《高等数学》课程教材没有把求极限的方法进行归纳总结，如果教员讲课照本宣科，那么，学员就更是一头雾水了.为了帮助学员掌握求极限的方法并能熟练地求极限，笔者对《高等数学》课程中常用的求极限的方法进行了分析研究，给出了每种方法的注意事项及使用技巧，并把一些方法推广到了二重极限，以弥补教材的不足.

1 利用极限的四则运算法则

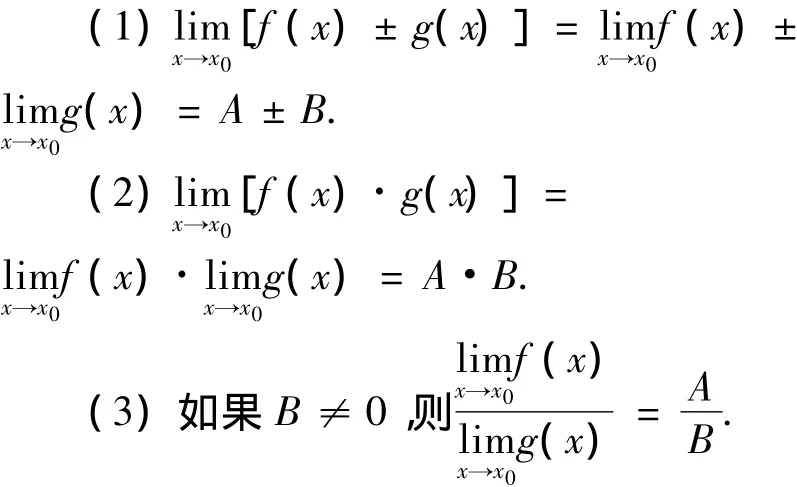
上述法则是以自变量x→x0的形式给出的，其实只要条件和结论是自变量的同一变化过程，那么法则均是成立的.另外，对于数列极限有类似的结论，这里不再赘述.

利用极限的四则运算法则求极限是最基本也是最常用的方法，很多求极限题目的最后一步都是用极限的四则运算法则来求的.

注1 极限的四则运算法则成立的前提条件有两个，其一是:函数(或数列)是有限项;其二是每一项的极限均存在.只要上述两个条件中的一个不成立，就不能用四则运算法则，这里的极限不存在也包含极限为∞、+∞及－∞这三种类型.

因此，在利用极限的四则运算法则求极限时，一定要满足其使用的前提条件，千万不能不管条件，“随心所欲”，否则就容易出错．

另外，极限的四则运算法则只能按照“从左到右”的顺序来用，千万不能按照“从右到左”的顺序来用．有的学员经常乱用，例如，设存在不存在．很多学员是这样证的:假设g(x)］存在，则+g(x)］－即存在，与已知矛盾，所以g(x)］不存在．

注3 当分母的极限为零时，商的运算法则就不能用了，此时可以有三种方法来处理:方法1是消去零因子;方法2是利用无穷小与无穷大的关系［1］;方法3 是利用洛必达法则［1］．当然，上述三种处理方法各有各的适用范围．方法1和方法3适合分子分母的极限都为零的情形，方法2适合分子的极限为非零常数的情形．例如，对于极限，既可以用消去零因子的方法计算，也可以用洛必达法则来计算，具体解题过程这里不再赘述．而对于极限，只能用无穷小与无穷大的关系计算，即:因为，所以原式=∞，故该极限不存在．

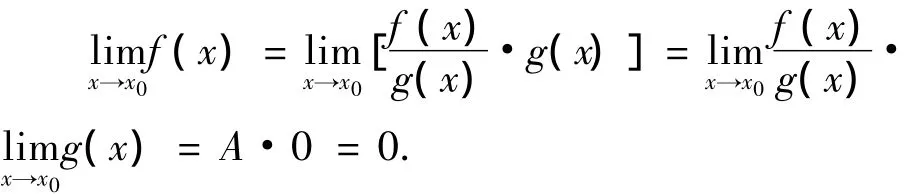
上述定理中是以自变量x→x0的形式给出的，其实只要条件和结论是自变量的同一变化过程，那么定理均是成立的，这里不再赘述．另外，上述定理可以直接应用，其主要应用就是确定极限式子中的常数和已知极限求另外的极限．例如，已知如果直接利用定理，则因为，所以必有，因此

注5 一元函数极限的四则运算法则可以完全推广到二元函数的二重极限，其成立的前提和使用原则完全与一元函数相同．

2 利用两个重要极限

定要理解该重要极限的实质，灵活应用．

注8 两个重要极限可以完全推广到二元函数，即若x0·y0=0，且当(x，y)→(x0，y0)时，有f(x，y)→0成立，则有等．

3 利用夹逼准则

夹逼准则是:如果数列{xn}、{yn}及{zn}满足下列条件:

(1)从某项起，即∃n0∈N，当n＞n0时，有yn≤xn≤zn．

函数极限有类似的结论，这里不再赘述．注意夹逼准则成立的两个条件，很多学员在应用夹逼准则时经常把条件(1)写成，这是不正确的．

注9 利用夹逼准则求极限的关键是构造出极限易求并且极限值相等的数列{yn}和{zn}．构造数列{yn}、{zn}的一般方法是从数列{xn}出发，适当放缩即可．一般地，当数列{xn}是n项相加时，把所有项的分母都放缩为分母中的最大项和最小项即可得数列{yn}和{zn}．例如，对于极限，可以构造数列

注10 如果数列是n项和式求极限，则一般有三种方法求解:方法1是利用数列求和的方法对这n项和进行化简．当然这里求和的方法有很多，常用的主要是初等数学所讲的等差、等比数列求和公式、拆项相消等．一般地，当这n项和式容易求和时就用该方法．方法2是利用夹逼准则．当这n项和式不易求和或根本无法求和，并且数列{yn}和{zn}容易构造时，就用夹逼准则．方法3是利用定积分的定义．当能从数列的n项和式中提出一个因子，而余下部分的每一项可以写成某个函数在一区间n等分点上的函数值时，就可以用定积分的定义来求［4］．其实当数列不是n项和式，而通过某种运算可以化为和式，并且满足上述条件时也是用定积分的定义来求极限的．另外，利用定积分的定义求数列极限的一般步骤是:首先，从各项中提出因子.这一步是相当于将［0，1］区间n等分，并且每个小区间的长度Δx=.然后，观察提出1后的剩余部n分，把和式写成的形式.这一步意味着在定积分的定义式中ξ取的是.其次，把函数fi中的换成x，即找到了函数f(x).最后，写出定积分，并计算该定积分即可.上述步骤只是用定积分的定义求数列极限的常用步骤，其实积分区间不一定非要是［0，1］，区间也不需要等分，ξi也不必非要取区间端点.但是，利用上述步骤容易正确写出定积分的形式.另外，有的题目需要夹逼准则和定积分的定义相结合才能计算出来，这里不再赘述.

注11 夹逼准则可以完全推广到二元函数乃至n元函数，对二元函数的夹逼准则可以描述为:如果函数f(x，y)、g(x，y)及h(x，y)满足下列条件:

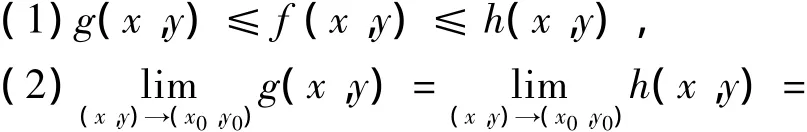
A，那么存在，且等于A.

上述结论利用二重极限的定义即可以证明，这里不再赘述.对于二重极限最常用的求解方法就是夹逼准则，其使用方法、使用原则及构造函数的技巧和一元函数一样.

4 利用单调有界准则

单调有界准则是:单调有界数列必有极限.

单调有界准则是针对数列而言的，函数极限不具有该准则.根据单调数列的性质，单调递增有上界数列必存在极限，单调递减有下界数列必存在极限.因此，对于单调递增数列，只需证出其有上界即可，对于单调递减数列，只需证出其有下界即可.

注12 使用单调有界准则证明极限存在时，既要证有界性又要证单调性.初学者经常是只证明其中的一个条件成立，另外一个条件往往忽略不证，这是错误的.另外，到底是先证有界性还是先证单调性，没有固定的模式，可以根据题目灵活处理.但是也有一定的技巧，依据确界原理及单调数列的性质，可以知道单调递增(递减)有上界(下界)的数列的上确界(下确界)必是其极限［5］.因此，在证明前不妨先求出其极限(当然极限存在的前提下)，然后随机找出数列的几项，看看这几项是比该极限值大还是小，由此判断该极限值到底是上确界还是下确界，从而既可以断定出该数列的界还可以判断出该数列是单调递增还是单调递减的，然后朝着目标严格证明即可.

一般地，当题目以文字叙述的形式给出时，例如“已知数列{xn}满足某种条件，证明该数列的极限存在，并求之.”常常用单调有界准则来证明，并且这类题目求极限的方法很固定，就是在题目所给等式的两边同时取极限，然后解方程，再依据极限的唯一性和保号性确定出极限值.

分析:该题目显然是用单调有界准则来证明的，但是到底是先证有界性还是先证单调性呢，下面不妨用所给的技巧进行分析.即设，解之得a=2或a=0，注意到该数列的特点可知a=2.又因为由此可知2是该数列的一个上界，因此该数列应该是单调递增的.根据所获得的上述信息，就可以严格按照解题步骤来证明了.需要注意的是，上述过程只是解此类题目的小技巧，解题过程是很不规范的，只能写在草稿纸上，千万不能作为正常的解题步骤，下面给出该题目严格的证明步骤.

证明 先证有界性:

再证单调性:

5 利用等价无穷小代换

等价无穷小代换定理是［1］:设 α～α'，β～β'，且存在，则lim

注意等价无穷小的实质及其满足的条件，常用的等价无穷小有:当函数u(x)→0时，或当x→0时，有函数u(x)→0成立，则有1－cosu(x)

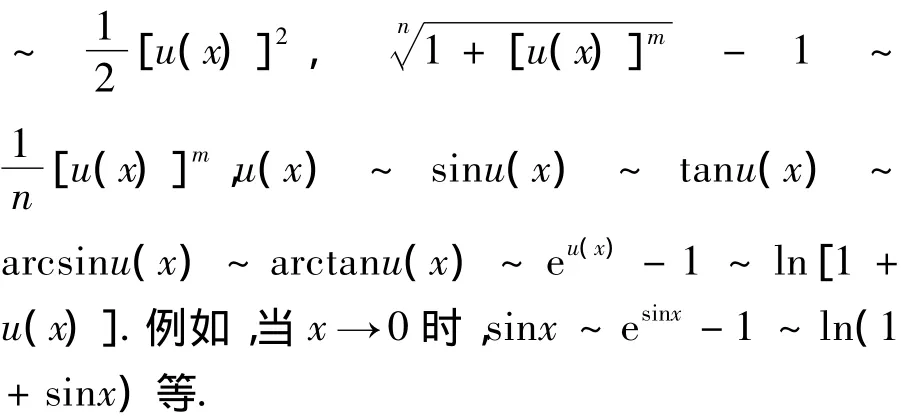
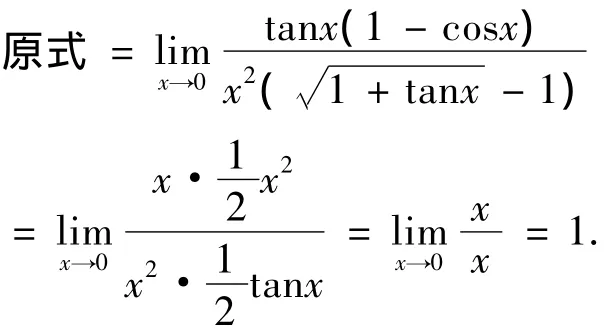
尽管利用等价无穷小代换求极限是一种非常有效的方法，但是使用该方法时必须满足其使用条件.

注14 利用等价无穷小代换求极限时，最好是对整个因子作代换，不要对因子中相加减的项作代换，如果要对因子中相加减的项作代换，就必须满足其前提条件.所以，建议大家使用等价无穷小代换求极限时只对整个因子作代换，如果出现和差项，先通过恒等变形，把其化成因子形式，然后再利用等价无穷小代换.例如对于极限可以按照下列方法处理:

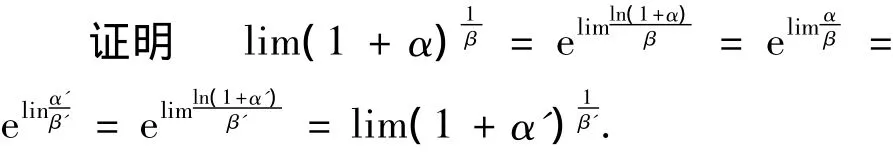
利用上述结论，可以简化幂指函数极限的运算.例如对于极限，就可以按照这样计算:原式

注16 等价无穷小的概念可以推广到二元函数，利用等价无穷小代换求极限可以推广到二重极限．对二元函数常用的利用等价无穷小有:若 x0·y0=0，且当(x，y)→(x0，y0)时，有f(x，y)→0成立，则有f(x，y)～sinf(x，y)～tanf(x，y)～arcsinf(x，y)～ef(x，y)－1～ln［1+f(x，y)］，1－cosf(x，y)～［f(x，y)］2．例如，当(x，y)→(0，0)时，x2+y～sin(x2+y)～ex2+y－1等．

另外，利用等价无穷小代换求二重极限的方法、使用条件及使用技巧与一元函数极限完全相同.

6 利用洛必达法则

洛必达法则是:设函数f(x)及F(x)满足如下条件:

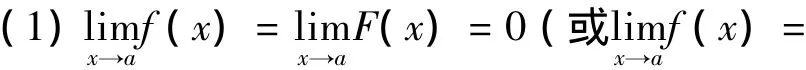
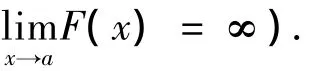
(2)f(x)和F(x)在内都可导，且F'(x)≠0.

上述定理中的三个条件缺一不可.另外，定理中的x→a换为自变量的其他变化趋势，只要条件(2)作相应的修改，定理仍然成立，这里不再赘述.

注18 对于数列极限，不能直接利用洛必达法则来计算，可以先把自然数n换成x，然后用洛必达法则求得函数的极限，最后依据归结原则［5］，就可以得到原数列的极限.例如，对于数列极限，可以按照下列方法求解.

例 2［6］求

解 原式=

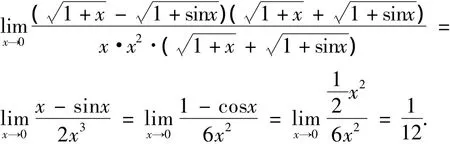
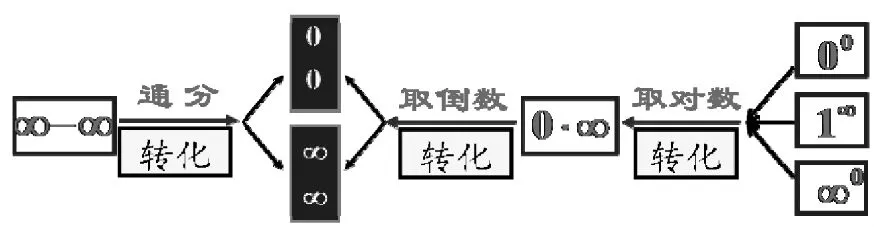
图1 其他形式的未定式转化为型的未定式的方法

7 结束语

当然，《高等数学》课程中求极限的方法还有很多，如可以利用导数的定义、泰勒公式、微分中值定理、无穷级数收敛的必要条件等，这里不再赘述.尽管求极限的方法有很多，每种方法也都有自己的适用范围，但是很多求极限的题目不是用一种方法就能解决的，它需要多种方法的结合才能解决，例如对于极限

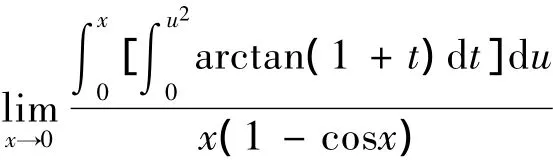
的求解，既需要用等价无穷小代换还需要用到洛必达法则、约去零因子及四则运算法则，具体的解题过程这里不再赘述;另外，很多求极限的题目也可以用很多方法来求解，比如对于极限的求解，既可以用等价无穷小代换，也可以用洛必达法则，当然也可以用两个重要极限，但是本题目最妙的求解方法就是利用洛必达法则，具体的解题过程也不再赘述.因此，大家在学习的过程中，一定要善于思考和归纳总结，总结各种方法的优缺点、使用条件及适用范围，这样遇到求极限的题目才能游刃有余、得心应手.另外，遇到一题有多种解法的题目，最好选择最简单、最方便的解法，因为数学蕴涵着和追求的是简单美和方法美.

［1］同济大学应用数学系.高等数学:上［M］.第六版.北京:高等教育出版社，2007.41–139.

［2］陈文灯，黄先开，等.高等数学复习指导——思路、方法与技巧［M］.北京:清华大学出版社，2009.37.

［3］张天德，蒋晓芸.吉米多维奇Б П.高等数学习题精选精解［M］.第一版.济南:山东科学技术出版社，2010.16.

［4］崔荣泉，褚维盘，等.高等数学重点内容重点题［M］.第一版.西安:西安交通大学出版社，2005.122.

［5］华东师范大学数学系.数学分析:上［M］.第三版.北京:高等教育出版社，2001.5–52.

［6］吴忠祥.工科数学分析基础教学辅导书:上［M］.第一版.北京:高等教育出版社，2009:161.