基于行车安全的连续轨道桥梁抗震设计研究

韩 艳，王晓东

(北方工业大学 土木工程学院，北京 100144)

基于行车安全的连续轨道桥梁抗震设计研究

韩 艳，王晓东

(北方工业大学 土木工程学院，北京 100144)

为探讨实用的轨道桥梁抗震设计方法，以轨道交通中广泛使用的连续轨道桥梁为研究对象，通过建立的地震荷载作用下车—轨—桥系统动力响应分析模型，模拟了列车在不同强度和卓越频率的人工地震波作用下过桥的全过程，分析了车辆类型、地震强度和频谱特征等因素对车辆与桥梁结构动力响应的影响;采用日本关于行车安全度的评价指标(脱轨系数、轮重减载率和横向轮轨力)作为地震时桥上车辆运行安全的评定标准，以列车脱轨临界状态时的桥梁动力响应作为桥梁振动的限值，统计得到了确保地震发生时列车安全运行的桥梁容许横向位移限值和横向加速度限值，绘制了桥梁振动限值曲线，并利用拉格朗日插值法得到曲线的数学表达式。研究结果表明，规范规定的桥梁横向位移限值有时不能满足地震作用下车辆运行安全的要求，对位于地震区的连续轨道桥梁横向振动位移限值的确定需要考虑地震动强度和频谱特性的影响。

行车安全 轨道桥梁 连续梁桥 容许限值 抗震设计

桥梁横向振幅是列车运行荷载作用下，桥梁结构的几何特性、物理特性以及动力特性在桥梁横向刚度上的综合反映［1］，为保证行车安全性，应当对桥梁横向振幅加以限制;而目前在我国的城市轨道交通设计中未见有对桥梁横向振幅行车安全限值的明确规定。本文以预应力混凝土箱形连续轨道桥梁为研究对象，通过车—轨—桥系统地震响应分析模型，根据《中国地震动参数区划图》中对地震强度的规定，采用三角级数法模拟生成不同强度和卓越周期的人工地震波，并将其分别输入到车—轨—桥系统地震响应分析程序中，计算车—轨—桥系统的地震响应，得到了确保地震发生时列车安全运行的桥梁容许横向位移限值和横向加速度限值，可供桥梁抗震设计时参考。

1 计算模型与分析方法

1.1 地震作用下车—轨—桥系统动力响应分析模型

车—轨—桥系统的地震响应分析模型由车辆子系统和轨道—桥梁子系统组成，两者之间由动态的轮轨关系发生联系。轨道不平顺为系统的自激激励源，地震作用作为外部激励施加在桥梁的支座处，通过影响矩阵使桥跨结构产生振动，由动态的轮轨关系对车辆产生影响;列车的振动反过来又通过动态轮轨关系对轨道桥梁结构的振动产生影响［2-4］。

车辆子系统是由机车和若干节客车车辆组合而成的列车，每节车辆又是由车体、转向架和轮对通过线性弹簧和阻尼器连接起来的多自由度振动系统，不考虑振动过程中车体、转向架构架和轮对的弹性变形。车体和转向架各有5个自由度，即横摆、侧滚、摇头、沉浮和点头;每个轮对均有横摆、侧滚、沉浮3个自由度。这样，对于二系悬挂4轴客车，每节车的计算自由度为27。

轨道—桥梁子系统一般由桥梁墩台、主梁、桥面系、桥上轨道等结构物组成，在研究桥梁和车辆的振动响应时，一般采用空间模型进行分析。假定桥上轨道和梁之间没有相对位移，即忽略钢轨垫板和扣件的弹性变形，对于箱梁结构，其横截面的变形可在振型分析中加以考虑。将二期恒载(包括道砟、钢轨、轨枕、扣件、人行道板)作为均布质量分配到相应的桥面单元中。为提高计算效率，轨道—桥梁模型中可采用模态综合技术，利用振型的正交性，把互相耦联的运动方程解耦，使其转化为互相独立的模态方程。

地震作用下车桥系统的动力平衡方程为

式中，下标“v”和“b”分别表示车辆和桥梁。方程左边的质量矩阵、阻尼矩阵、刚度矩阵和位移向量，方程右边的轮轨间作用力Fv和 Fb，以及地震力向量 F*v和F*b的推导详见文献［4］。

根据以上理论编制了仿真计算程序，并用于本文的研究。

1.2 计算参数及分析方法

连续梁桥具有内力状态均匀合理、桥下净空大、节省材料、刚度大、整体性好、跨度大等优点，在我国城市轨道交通中有较广泛的应用。本文选取一座(32+54+32)m的双线预应力混凝土连续轨道桥梁作为研究对象。该桥桥宽为9.2 m，两中墩处的箱梁为3.2 m高的等截面形式，两边墩处的箱梁为1.8 m高的实腹等截面形式，从距中墩中心1 m至边墩中心8.9 m之间梁高按二次抛物线变化，在各跨的中间均设置0.2 m厚的横隔板，其立面布置如图1所示。主梁典型的横断面尺寸参见图2和表1，墩柱的立面和典型断面如图3所示。

图1 桥梁立面(单位:cm)

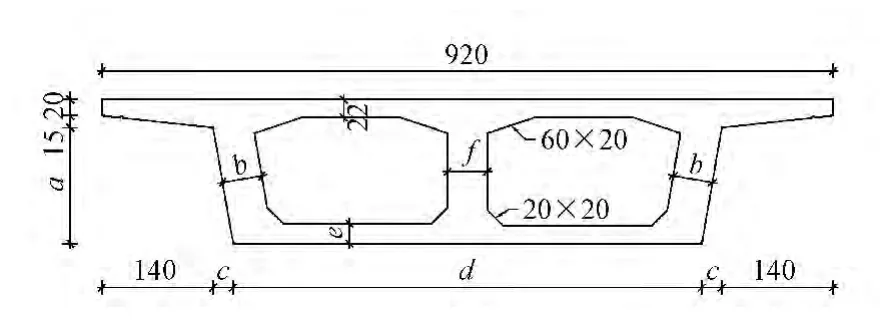
图2 主梁典型横断面示意(单位:cm)

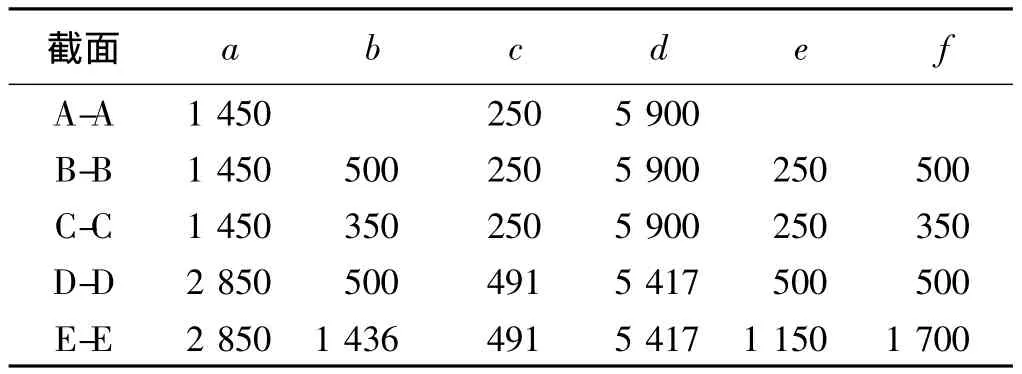
表1 主梁截面尺寸 mm

图3 桥墩构造示意(单位:cm)

为考虑相邻后继结构对桥梁抗震性能的影响，采用Midas/Civil软件建立了两联的连续梁桥有限元模型，主梁、桥墩和桩基础均采用三维梁单元来描述，主梁与墩顶之间的支座采用一般连接中的滞后系统［5］来模拟，桩土之间的相互作用采用节点弹性支承模拟，弹性支承的刚度按桥梁规范中的“m”法计算［6］，钢轨及轨道结构的自重视为二期荷载直接作用于桥梁上，其线荷载集度为104.9 kN/m。

桥梁结构的自振频率和振型是结构动力性能的综合反映，采用多重 Ritz向量法进行特征值分析，共计算了90阶模态，桥梁模型顺桥向、横桥向和竖向的振型参与质量分别达到了99.77%，99.68%，99.98%，均满足规范［7］中＞90%的规定。桥梁结构的前10阶自振周期及相应的振型列于表2中。

计算车辆模型选取国产高速列车(1机+5客+1机)、Chinastar高速列车(1机 +9客 +1机)和德国ICE高速列车(1机+14客+1机)三种列车，相应各列车的主要车辆计算参数列于表3中。为引用方便，这三类车辆分别记为 Gch，Chinastar，ICE。

采用日本关于列车脱轨安全度评价的C限度限值(脱轨系数Q/P=1.2、轮重减载率 ΔP/P=0.67、轮对横向水平力Q=78 kN)作为评价地震时轨道桥梁上列车运行安全的标准;即如果车辆的脱轨系数、轮重减载率和轮对横向水平力中有一个数值达到列车运行安全限值，就表明车辆处在安全与危险的临界状态，此时的轨道桥梁动力响应值就是能保证地震时桥上列车运行安全的最大容许值。分别计算在不同强度、不同卓越周期人工地震波作用下，不同车辆以不同速度通过连续轨道桥梁时的车桥动力响应，并对仿真计算结果进行统计分析，最终得到在不同强度地震动作用下能够保证车辆运行安全的桥梁横向位移和横向加速度限值。

表2 桥梁前10阶自振周期及振型计算结果

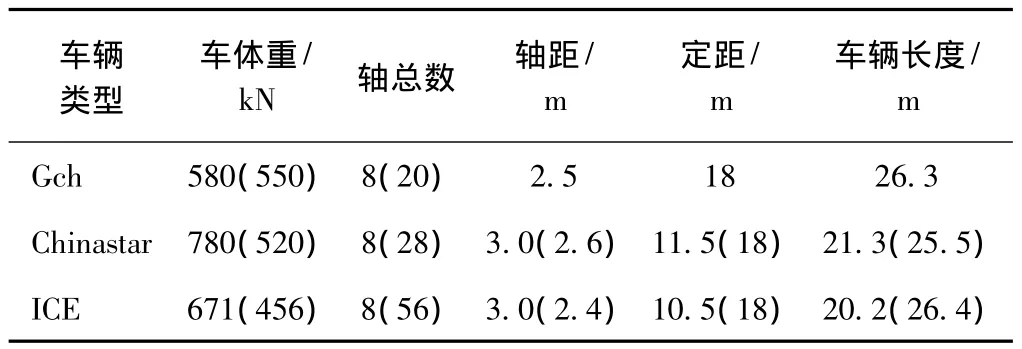
表3 计算列车主要参数

2 计算结果

表4为在峰值加速度为0.5 m/s2的不同卓越频率的地震波作用下，能保证以上三种不同列车安全通过连续轨道桥梁的桥梁动力响应限值。

由表4可见，在相同强度及卓越频率的地震动激励下，采用不同的列车类型计算得到的桥梁横向位移限值以及横向加速度限值基本一致。这表明，能保证地震时车辆运行安全的桥梁横向位移限值和横向加速度限值受桥上运营车辆类型的影响很小，可不考虑车辆类型对桥梁横向振动限值取值的影响，而近似地采用一种车辆类型来研究临界状态时的桥梁横向振动响应。

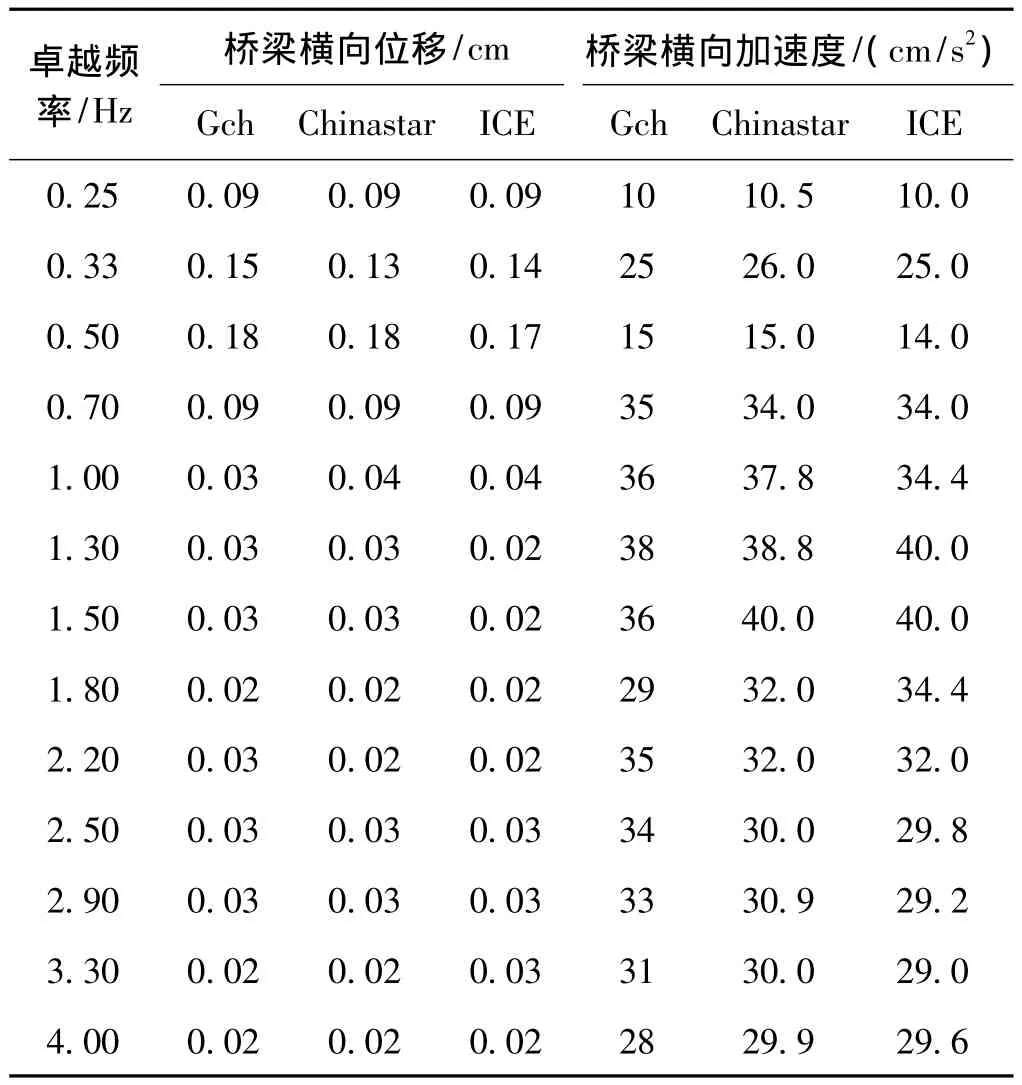
表4 0.5 m/s2地震波作用下桥梁的横向动力响应限值

表5为在不同地震动强度、不同卓越频率人工地震波作用下，Chinastar列车处于脱轨临界状态时的车辆运行安全评价参数值，其中加粗部分为车辆临界状态时的控制参数。具体地表示，若车速再增加1 km/h，则脱轨系数、轮重减载率和轮对横向水平力中就会有一个指标超过上述的列车运行安全限值，那么该车速即为脱轨时的临界车速，此时的桥梁动力响应即为能保证行车安全的容许限值。

从表5可以看出:

1)对相同强度的地震动作用来说，当地震波的卓越频率≥1.8 Hz时，能保证车辆安全运行的临界车速变化不大，表明地震波中的高频成分对列车运行安全的影响很小。

2)以一定强度、不同卓越频率地震动作用下临界车速值作为此强度地震作用下保证桥上车辆安全运行的速度限值。可以看出，随地震动强度的增大车速限值逐渐减小，当地震动强度由0.05g增大到0.2g时，车速限值由 155 km/h降低到 50 km/h，降幅为67.7%。

3)脱轨系数、轮重减载率和轮轨力均有可能成为车辆脱轨临界状态的控制参数，这也反应了车辆脱轨的随机性。

图4为Chinastar列车在不同强度地震动作用下通过连续轨道桥梁时的桥梁横向动力响应限值与地震波卓越频率的关系图。

表5 临界状态时的车辆行车安全性参数值

图4 Chinastar过桥时桥梁的横向动力响应限值

从图4可以看出:

1)地震动强度是影响地震时轨道桥梁上车辆运行安全的重要因素，在地震动卓越频率一定时，随着地震动强度的增大，临界状态时的桥梁横向位移值和横向加速度值也相应地增大，尤其是在低频区域。

2)地震动作用的卓越频率对地震时桥上车辆运行的安全性有较大的影响:在0～1.0 Hz的卓越频率范围内，连续轨道桥梁的横向振动限值变化很大，在＞1.0 Hz的卓越频率范围内连续轨道桥梁横向振动限值变化较平缓。

由图4中的桥梁横向振动位移限值曲线特征，可将其分为三段:上升段、下降段、稳定段。若引入参数α表示地震动强度的影响并采用拉格朗日插值方法，可得到连续轨道桥梁横向振动位移限值d的数学表达式为

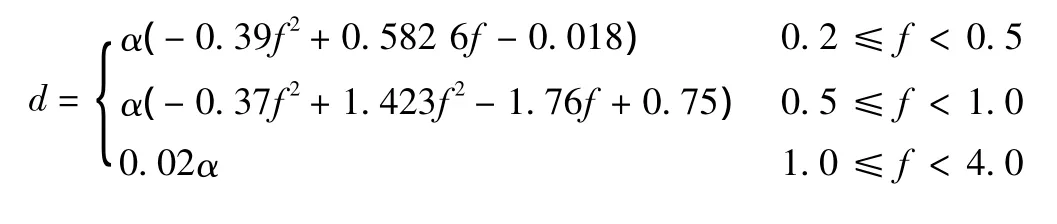
式中:f表示地震动的卓越频率;α为表示地震动强度影响的参数，当地震动强度分别为 0.05g，0.10g，0.15g，0.20g 时，α 分别取 1，2，3，4。

图5为0.05g，0.10g，0.15g和0.20g四种地震动强度情况下，由式(2)计算得到的连续轨道桥梁横向振动位移限值曲线与仿真计算数据曲线的对比。

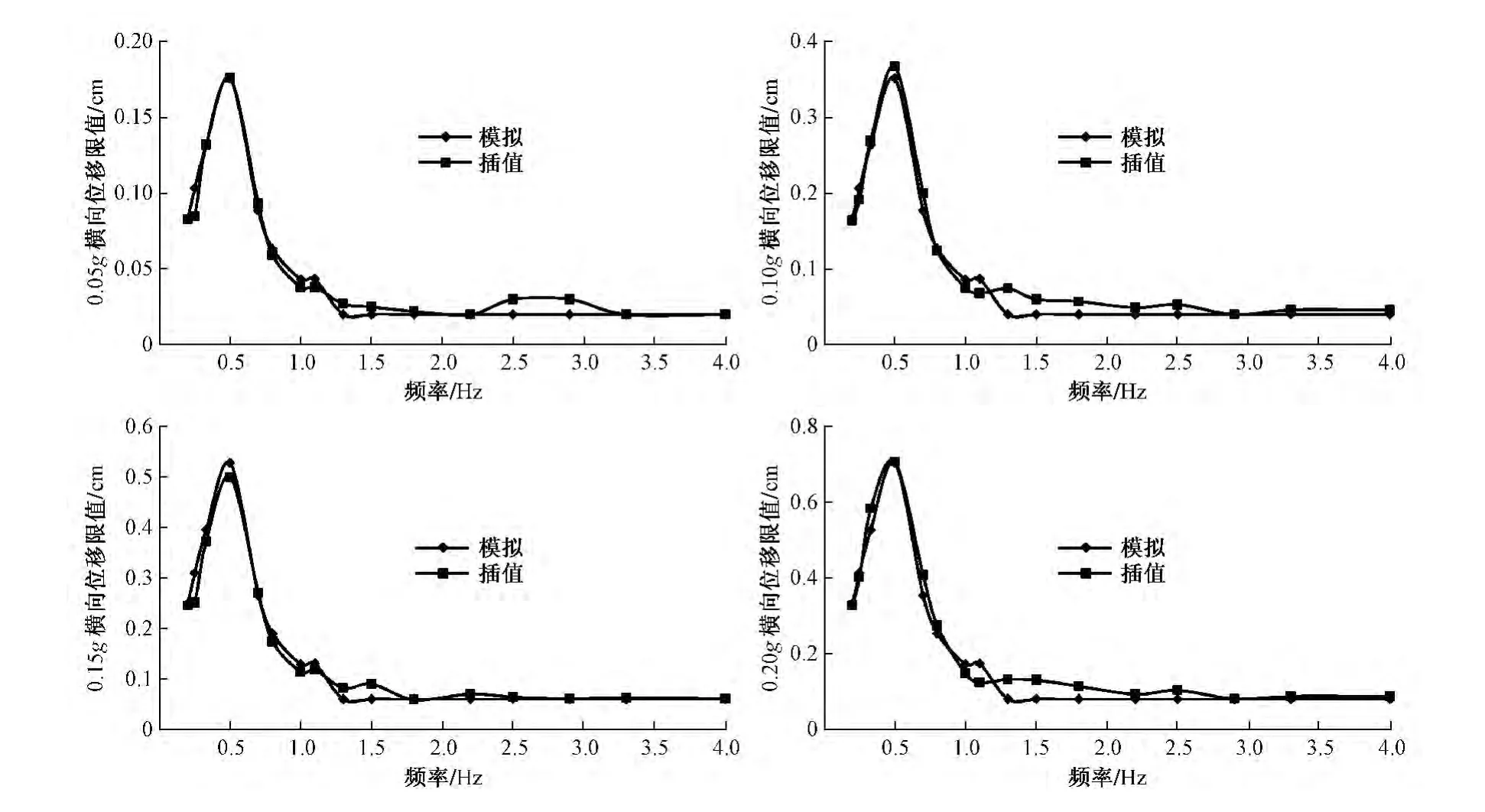
图5 插值数据与仿真数据的对比

从图5中可以看出，插值数据曲线与仿真模拟数据曲线基本吻合，表明拉格朗日插值数据符合数值插值的精度要求，可以采用式(2)来简化计算连续轨道桥梁的横向振动位移限值。

在桥梁设计时，取拟建桥址处的地震波进行桥梁地震反应分析，可以得到桥梁横向位移最大值和加速度最大值;与公式(2)中相应的限值进行比较，可以判断出桥梁的横向刚度是否足够保证列车安全运行以及桥梁的尺寸是否合理，从而免去了繁琐的车桥动力相互作用分析，提高了桥梁设计效率。

目前，我国《铁路桥梁检定规范》［8］中规定桥跨结构梁体水平横向挠度应小于或等于计算跨度的L/9 000(L为连续梁桥的跨度)。图6为由式(2)计算得到的连续轨道桥梁横向振动位移限值与该规定值的比较图。

从图6中可以看出，地震作用对连续轨道桥梁上车辆运行的安全性有较大的影响。就本文的计算工况来说，仅当地震动强度为0.2g且卓越频率为0.3～0.7 Hz很小的范围内计算值大于规范值，其余的横向位移限值均小于规范值。这表明基于规范规定的桥梁横向位移限值不能满足地震作用下行车安全的要求，对位于地震区的连续轨道桥梁横向振动位移限值的确定需要综合考虑地震动强度和频谱特性的影响。

图6 插值数据与规范值的比较

3 结论

本文从保证地震时轨道桥梁上车辆运行安全的角度，采用结构动力学与车辆动力学的理论方法，对连续轨道桥梁的容许限值问题进行了较系统的研究，主要结论如下:

1)地震作用下连续轨道桥梁结构的横向位移和横向加速度响应受列车类型的影响很小，可采用能保证行车安全的桥梁横向位移最大值或横向加速度最大值作为桥梁的抗震设计指标。

2)地震动的强度和频谱特性对轨道桥梁上列车的走行安全性有较大的影响，针对不同的场地类别和地震动分组，可以绘出相应于不同强度和频谱特性地震动时的桥梁的横向容许位移限值和横向加速度限值，供轨道桥梁抗震设计时使用。

3)基于规范规定的桥梁横向位移限值有时不能满足地震作用下行车安全的要求，对位于地震区的连续轨道桥梁横向振动位移限值的确定需要考虑地震动强度和频谱特性的影响。

［1］翟婉明，夏禾．列车—轨道—桥梁动力相互作用理论和工程应用［M］．北京:科学出版社，2011．

［2］潘家英，高芒芒．铁路车—线—桥系统动力分析［M］．北京:

中国铁道出版社，2008．

［3］韩艳，夏禾，张楠．考虑非一致地震输入的车—桥系统动力响应分析［J］．中国铁道科学，2006，27(5):46-53．

［4］韩艳．地震作用下高速铁路桥梁的动力响应及行车安全性研究［D］．北京:北京交通大学，2005．

［5］葛俊颖．桥梁工程软件 Midas Civil使用指南［M］．北京:人民交通出版社，2013．

［6］中华人民共和国住房和城乡建设部．GJJ 166—2011 城市桥梁抗震设计规范［S］．北京:中国建筑工业出版社，2011．

［7］中华人民共和国住房和城乡建设部．GB 50011—2010 建筑抗震设计规范［S］．北京:中国建筑工业出版社，2010．

［8］中华人民共和国铁道部．铁运函［2004］120号 铁路桥梁检定规范［S］．北京:中国铁道出版社，2004．

Research on seismic design of continuous track bridge based on running safety

HAN Yan，WANG Xiaodong

(College of Civil Engineering，North China University of Technology，Beijing 100144，China)

Continuous track-bridge in rail transport was studied and the track bridge seismic design methods were discussed in this paper．A model of the train-track-bridge system under seismic loads was established to analyze the dynamic response．Artificial seismic waves with different intensity and frequency were selected．The whole history of the vehicles running through the bridge was simulated and the dynamic responses of the bridge and the vehicles were calculated．The influences of train type，seismic intensity and spectral characteristics of the earthquake were analyzed．The Japan traffic safety indexes including derailment coefficient，wheel offload rate and lateral wheel-rail force were introduced to evaluate the operation safety during earthquake． With statistic analysis，the allowed lateral bridge displacement limits and acceleration limits were obtained．The bridge vibration limit curve was drawn．By using Lagrange interpolation method，the mathematical expression of the curve was obtained．The results reveals that the lateral displacement limit calculated from current specifications cannot meet the requirement for operation safely during earthquake．Thus，the ground motion intensity and the spectrum characteristics should be considered when determining the continuous track bridge lateral displacement limits in seismic zones．

Running safety;Track bridge;Continuous beam bridge;Allowed limits;Seismic design

U442.5+5

A

10．3969/j．issn．1003-1995．2015．07．01

1003-1995(2015)07-0001-06

2014-12-08;

2015-04-30

北京市自然科学基金资助项目(8112013)

韩艳(1970— )，女，江苏滨海人，副教授，博士。

(责任审编 孟庆伶)