分布式光纤传感技术应用于PVC沉降管的试验研究

强小俊，张长生，郎向伟，蓝坤雄

(中国铁道科学研究院 深圳研究设计院，广东 深圳 518055)

分布式光纤传感技术应用于PVC沉降管的试验研究

强小俊，张长生，郎向伟，蓝坤雄

(中国铁道科学研究院 深圳研究设计院，广东 深圳 518055)

推导了由粘结于PVC沉降管的分布式光纤测试应变计算沉降管竖向挠度的差分计算方法，并将由该方法计算出的挠度值与试验中应用百分表实测的挠度值进行了对比分析。研究结果表明:利用分布式光纤测试应变计算出的挠度值所绘制的挠度曲线图较好地反映了荷载作用下PVC管的变形特性，计算值与实测值呈现良好的线性关系;根据线性拟合关系式计算出的挠度值与实测挠度值非常接近，最大相对误差的绝对值在8%以内，平均为3.44%，证明了所采用的挠度值差分计算方法及拟合公式可靠、实用。

分布式光纤 传感器 PVC沉降管 差分算法

光纤传感技术在工程监测领域的应用是近年发展起来的一种新技术，与传统的电类传感器或机械传感器相比，其具有抗电磁干扰、耐腐蚀、质量轻、体积小、兼备传感和传输功能、寿命长、可实现远距离监测与传输、使用期限内维护费用低等优点。光纤传感器可以用来传感多种物理量，具有良好的可靠性、耐久性，适合工程结构的长期实时监测［1］。

分布式光纤传感技术最显著的特点就是它可以准确地测出光纤沿线任一点上的应力、应变、温度、振动和损伤等信息，具有多参数、全分布式测量的优点，能够克服传统点式监测方式漏检的弊端，提高监测的成功率，在规模效益上体现出了一定的经济优势［2］。

目前国内外在分布式传感技术的工程应用方面做了很多研究工作［3-6］。本文探讨的是通过将分布式光纤粘附在PVC管上，用来测试被测对象的应变分布。

1 分布式传感技术原理

分布式传感技术目前主要有BOTDA和BOTDR两种，本文所应用的技术是前一种，其测量原理是:在光纤两端分别输入脉冲光和连续探测光，当两者的频差与光纤中某区域的布里渊频移相等时，则在该区域就会产生受激布里渊(SBS)放大效应，两光束之间发生能量转移。当光纤沿线的温度发生变化或者存在轴向应变时，光纤中的背向布里渊散射光的频率将发生漂移，频率的漂移量与光纤应变和温度的变化呈良好的线性关系，因此通过测量光纤中的背向布里渊散射光的频率漂移量就可以得到光纤沿线温度和应变的分布信息。光纤应变量、温度变化量与布里渊频率漂移量之间的关系式为

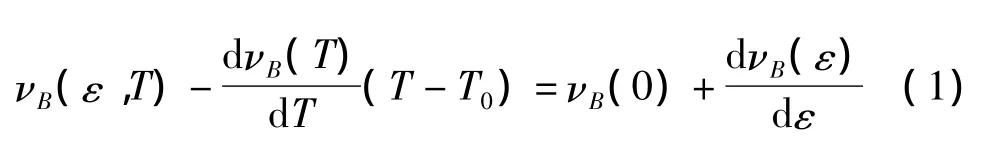
式中:νB(ε，T)为在应变 ε、温度 T时的布里渊频率漂移量，dνB(T)/dT为温度比例系数，T－T0为光纤温度差，νB(0)为初始应变与温度时的布里渊频率漂移量，dνB(ε)/dε 为应变比例系数。

2 室内试验

2.1 试验装置及方法

试验装置如图1所示。整个装置由混凝土墩、钢梁、螺母、百分表、PVC管等构件组成。沿PVC管下侧的预设槽内布设分布式光纤，通过调节螺母对PVC管逐级施加竖向位移，模拟沉降管变形。PVC沉降管下方布置了5个百分表读取其下方5个测点的变形值，百分表间距0.3 m。PVC管直径为70 mm，长度为2 m。将0.9 mm的分布式光纤粘贴于PVC管的预制槽内并涂胶覆盖后，将PVC管固定在两端的混凝土支座上。试验步骤如下:

图1 分布式光纤PVC沉降管试验装置

1)首先用220#～400#粒度砂纸打磨 PVC沉降管的预设槽及待粘贴光缆，除去表面的脱模剂并用酒精棉擦拭干净。先在预设槽底部刷上适量的粘结剂，将光缆逐步平铺放入，一边放一边用聚四氟乙烯膜轻轻按压光缆，使其与PVC管充分粘结。

2)将粘结好光纤的PVC管按照简支的形式固定在两侧的混凝土支座上，在规定的测点处安装5个百分表，将百分表调零并调节好BOTDA解调仪。

3)通过调节中间的螺母对PVC管逐级施加竖向位移，每次加载约2 mm，共进行5级加载。

4)每级荷载加载完毕稳定10 min后，记录各测点的百分表读数及光纤频移读数，并根据相应公式计算出各测点的百分表实测挠度值和应变值。

2.2 分布式光纤PVC沉降管数据处理方法

PVC 沉降管横截面形心在竖直方向的线位移f称为该截面的挠度。分布式光纤PVC沉降管变形后的轴线是一条平滑的连续曲线，满足平截面假定，并忽略剪力对弯矩的影响。沉降管曲率与弯矩之间的关系为

式中:k为沉降管曲率;M为弯矩;E，I分别为沉降管的弹性模量、惯性矩。

本文参照文献［7］提出的差分方法计算沉降管的挠度。设有数列{xn}，定义差分算子 Δxn=xn+1－xn为 xn在n处的向前差分，而 Δxn=xn－xn－1为 xn在 n处的向后差分。可见Δxn是n的函数，从而可以进一步定义 Δxn的差分 Δ(Δxn)=Δ2xn，称之为 xn在 n处的二阶差分，它反映的是增量的增量。二阶差分方程如下

式中:Δx为相邻两测点的间距，分布式PVC沉降管的应力与应变的关系可表示为

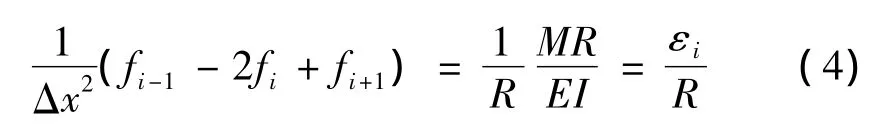
式中:R为测斜管的外径，εi(i=1～n)为第 i测点的应变。

上述方程改成矩阵形式如下

式中:f0，fn+1分别为沉降管两端的挠度值，n为沉降管测点的数量。

由于f0=fn+1=0，代入式(5)中，得到

可将式(6)中的系数矩阵第1，第n+2列忽略，可改写成以下矩阵形式

式(7)中系数矩阵为方阵且可逆，通过求逆矩阵，可以直接求得测点位移与应变的关系，见式(8)

3 试验数据分析

表1为分布式光纤测得的应变代入式(8)计算出的挠度值与百分表实测挠度值的比较。可以看出:实测值与计算值的相对误差较大，但是相对误差分布较均匀，主要集中在20% ～30%，平均值为24.77%。

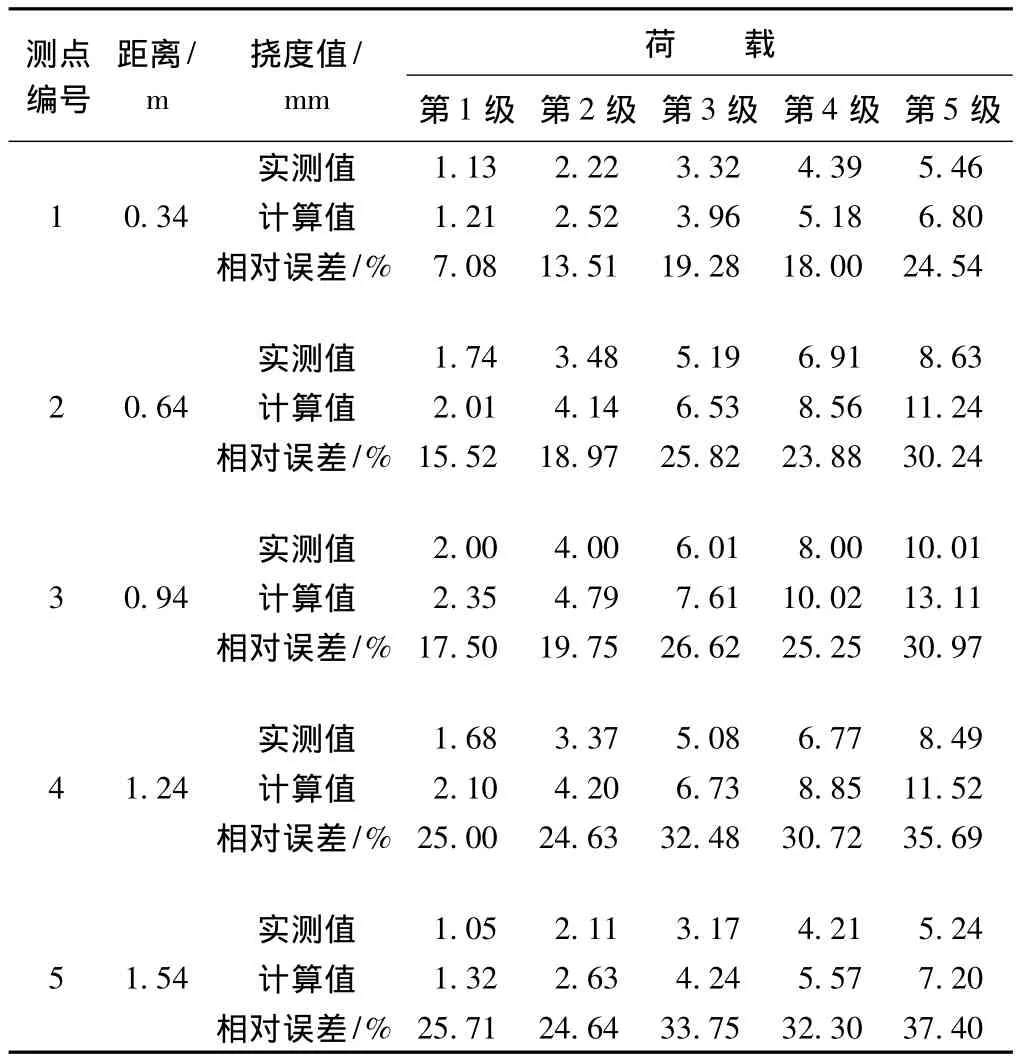
表1 各级荷载作用下挠度实测值与分布式光纤测试应变计算值的比较

图2为PVC沉降管在各级荷载作用下实测挠度曲线和分布式光纤应变计算挠度曲线图。可以看出，计算挠度曲线与实测挠度曲线非常相似，能较好地反映荷载作用下PVC沉降管的变形特性。

将表1中各测点的实测挠度值与计算挠度值进行线性拟合。图3为不同测点在各级荷载作用下计算挠度值与百分表实测挠度值的线性拟合关系，可以明显看出两者呈良好的线性关系，可用下式表达

式中:Y为拟合挠度值;X为计算挠度值;a，b为拟合系数。

从拟合结果可知:a大约分布在0.71～0.78，平均值约为0.74;b大约分布在0.17～0.34，平均值约为0.26;相关系数约为0.998。将表1中的分布式光纤应变计算挠度值代入式(9)，并采用平均拟合系数计算出拟合挠度值，见表2。可以看出，拟合挠度值与百分表实测的非常接近。除5号测点在第一级荷载作用下的相对误差为18.10%外，其余测点在各级荷载作用下的最大相对误差的绝对值控制在8%以内，平均为3.44%。

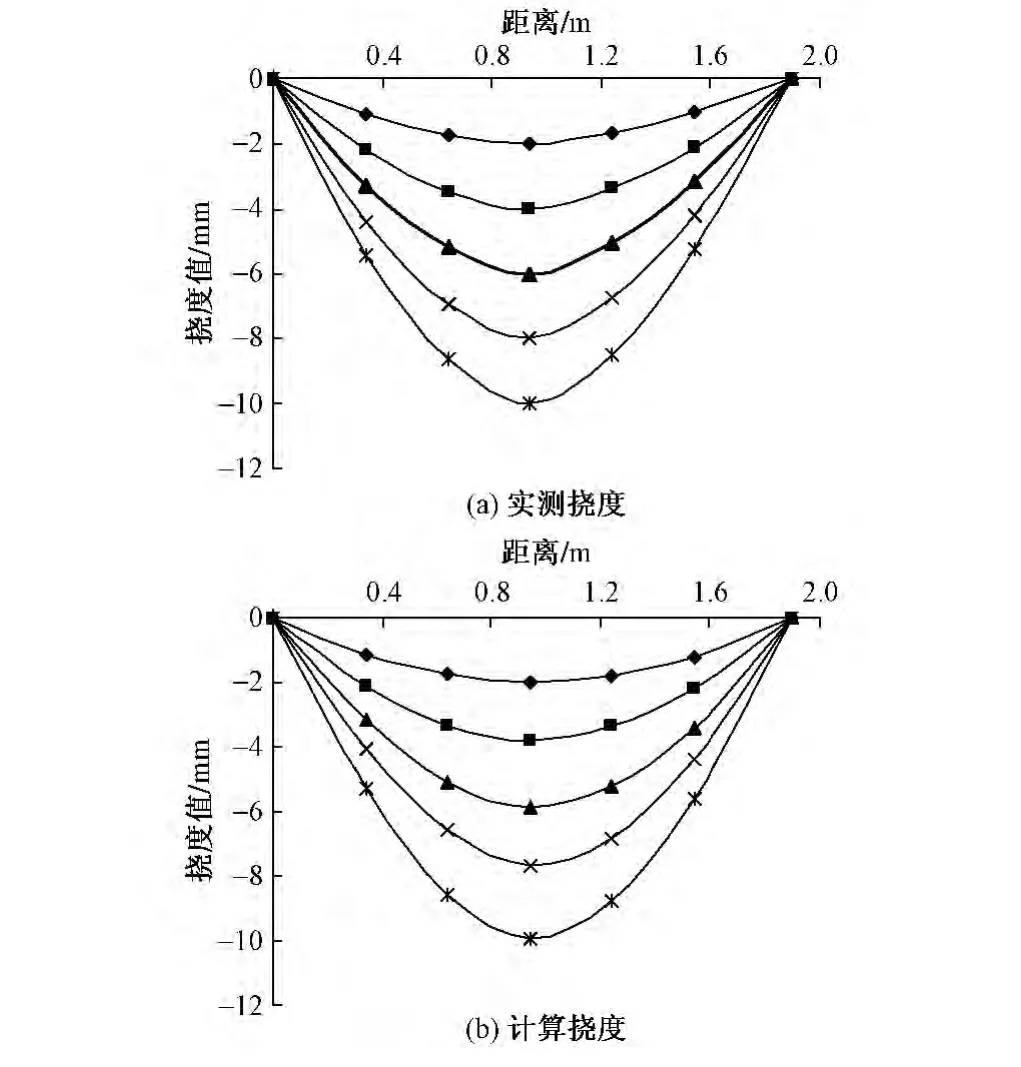
图2 PVC沉降管挠度曲线

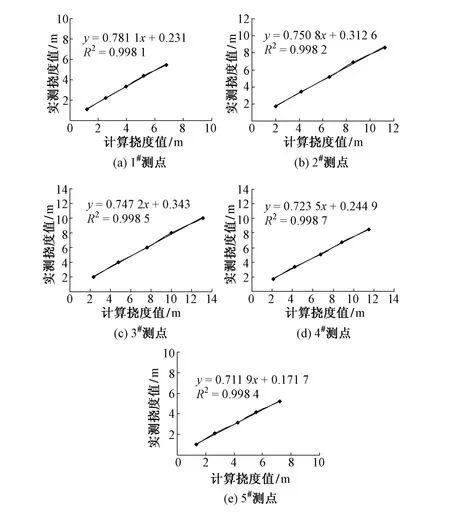
图3 拟合关系

图4为各级荷载作用下实测挠度曲线与拟合挠度曲线。可明显看出，两者非常吻合，进一步说明本文采用差分公式计算挠度的方法及拟合公式可靠、实用。

表2 各级荷载作用下挠度实测值与公式拟合计算值的比较

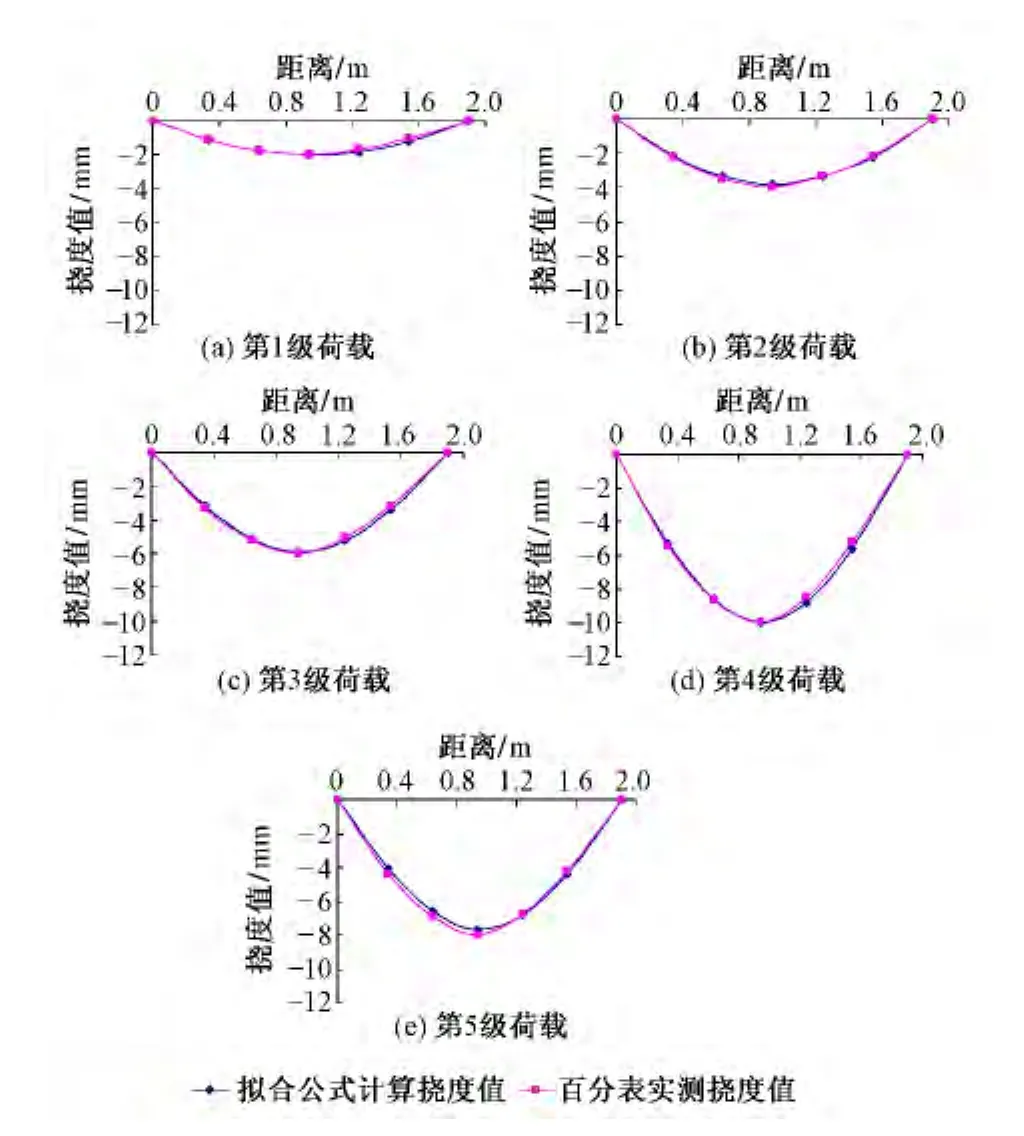
图4 不同荷载作用下实测挠度曲线与拟合挠度曲线

4 结语

本文对分布式光纤应用于PVC沉降管的传感技术进行了试验研究，根据差分法将分布式光纤测试的沉降管应变转化为挠度值，并与实测的沉降管挠度值进行了对比分析，得出如下结论:

1)利用分布式光纤测试的应变计算出的挠度值所绘制的挠度曲线较好地反映了荷载作用下PVC管的变形特性，且计算挠度值与实测挠度值呈现良好的线性关系。

2)根据线性拟合关系式计算出的挠度值与实测挠度值非常接近，最大相对误差的绝对值在8%以内，平均为3.44%，证明了本文采用差分法计算挠度值的方法及拟合公式可靠、实用。

3)分布式光纤应用于PVC沉降管的传感技术可行，下一步会将该技术应用于现场试验以进一步验证其适用性。这有助于分布式光纤传感技术的推广和应用。

［1］马水山，王志旺，李端有，等．光纤传感器及其在岩土工程中的应用［J］．岩石力学与工程学报，2001，20(增):1692-1694．

［2］张丹，施斌，徐洪钟．基于 BOTDR的隧道应变监测研究［J］．工程地质学报，2004，12(4):422-426．

［3］蔡德所．光纤传感技术在大坝工程中的应用［M］．北京:中国水利水电出版社，2002．

［4］施斌，徐洪钟，张丹，等．BOTDR应变监测技术应用在大型基础工程健康诊断中的可行性研究［J］．岩石力学与工程学报，2004，23(3):493-499．

［5］朴春德，施斌，魏广庆，等．分布式光纤传感技术在钻孔灌注桩检测中的应用［J］．岩土工程学报，2008，30(7):976-981．

［6］SHIBA K，KUMAGAI H，WATANABE K，et al．Fiber Optic Distributed Sensor for Monitoring of Concrete Structures［C］//The 3rd international workshop on structural health monitoring，Stanford University，2001:459-468．

［7］裴华富，殷建华，朱鸿鹄，等．基于光纤光栅传感技术的边坡原位测斜及稳定性评估方法［J］．岩石力学与工程学报，2010，29(8):1570-1576．

TU472.99

A

10．3969/j．issn．1003-1995．2015．07．40

1003-1995(2015)07-0142-04

2014-08-13;

2014-09-30

中国铁道科学研究院基金项目(SZY201205)

强小俊(1981— )，男，安徽芜湖人，副研究员，博士。

(责任审编 李付军)