星图识别的一种扩充栅格算法

钱华明，孙 龙，蔡佳楠，黄 蔚

(哈尔滨工程大学自动化学院，150001哈尔滨)

精确的姿态信息是航天器完成航天任务的基础.能够提供姿态信息的测量器件有很多，但是精度最高应用最广泛的是星敏感器.星敏感器的姿态确定过程分星空成像、星点提取、星图识别和姿态计算4个步骤.其中星图识别是星敏感器姿态确定的决定性阶段.对于星敏感器而言，星图识别的实质就是寻找观测星图中观测星在导航星表中对应的导航星［1］.

随着星敏感器的发展，出现了许多的星图识别算法.Padgett和Kreutz-Delgado等将星图识别算法划分为两种类型［2］.第一种类型是子图同构类算法，这类算法把观测星图看成是全天星图的子图，将星点作为顶点，利用星点的星等和它们之间的角距等信息，以线段、三角形、多边形等作为基本元素来进行星图识别［3］.其中最具代表性的有三角形算法［4］、匹配组算法［5］.另一种类型是模式识别类算法，这种算法为每颗星构造一个独一无二的特征“星模式”，这样星图识别的实质就是在星表中寻找与观测星模式相近的导航星.其中，比较有代表性的有栅格算法［2］、基于统计特征的识别算法［6］.

在这两类算法中，三角形算法的应用最广泛.然而三角形算法容易受到噪声的干扰，对噪声的鲁棒性较差，因此只能适用于噪声水平较低的情况.文献［7］针对各种噪声对比了三角形算法、匹配组算法与栅格算法，结果表明栅格算法的噪声鲁棒性要远远高于三角形算法和匹配组算法.然而栅格算法要求视场中观测星的数目不小于6颗［8］，这就限制了该算法在小视场、低星等敏感极限星敏感器中的应用.文献［9-10］中介绍了一种扩充星图的方法，利用陀螺的输出和前一时刻的识别信息将星图进行扩充，使得星图中星点数目增加，从而达到算法要求的限度.然而扩充星图法在星图识别阶段采用的是三角形算法，因此无法摆脱三角形算法本身的缺陷，容易受到噪声的影响.星敏感器本身存在着暗电流噪声、畸变噪声等，同时在航天器执行任务时会不可避免地受到环境的影响从而引入一定的噪声，在这种情况下，扩充星图算法的使用会受到很大的限制.

若将扩充星图的思想与栅格算法结合，利用扩充星图的方法来获取更丰富的星点信息，利用栅格算法进行星图识别，既能够打破栅格算法的限制，又可以利用栅格算法在星图识别阶段提高算法对噪声的鲁棒性，增加星图识别成功率，这就是本文的扩充栅格算法.与现有的扩充星图方法相比，扩充栅格算法能够继承栅格算法优势，拥有更好的噪声鲁棒性，更加适用于噪声水平较高的复杂环境.不管是扩充星图法还是本文的扩充栅格法都用到了陀螺的输出信息，因此扩充星图中必定存在由陀螺漂移引入的噪声，研究这些噪声对星图识别的影响是十分必要的.这是原始扩充星图法中忽略的一项，在本文中对其进行了详细的分析并在仿真环节进行了验证.

新算法用到了陀螺的输出和前一时刻的识别结果，不属于全天识别算法，文献［11］将这种类型的算法命名为递归模式算法，这种模式的算法适用于星敏感器的跟踪模式.因此，为了使得整个星图识别过程完整地运行，在初始姿态捕获模式本文选用了Pyramid算法，这种算法解决了太空迷失问题(lost in space)，已经被成功地应用到实际飞行器中［12］.

1 算法描述

1.1 栅格算法

原始的栅格算法栅格图像生成过程见图1，具体执行步骤［2，7］:1)从拍摄星图中选取一颗星作为待识别星(参考星又叫主星)，然后将其连同其邻域半径pr一起移动，使得其移动到视场中央.2)决定近邻星，近邻星是在参考星邻域半径pr之内，半径br以外离参考星最近的星.3)以参考星和近邻星连线为基准，以主星为中心旋转星图，使得星图的x轴穿过近邻星.4)生成g×g栅格，得到一个有g2个元素的矢量，有伴星的网格为1，否则为0，从而得到一个参考星的星模式s=［a1a2…am］.

图1 原始栅格算法

将参考星的星模式与存储在数据库中的星模式进行对比，若与星库中第i颗星的星模式的相同元素数目超过门限值ξ，则认为两颗星匹配.若任意视轴下匹配星的数目超过两颗，则认为此次星图识别成功.

从栅格的形成过程可以看出，近邻星的缓冲半径br和星图某一坐标轴方向上的栅格数目g控制栅格的形成过程，从而决定栅格算法的性能.若g较大，则每个栅格就较小，此时位置噪声对算法的影响较大.但是g较大时能够保证星图中的星点充分被利用，使得一个是栅格中出现多颗星的概率降低，星模式有足够多的维数进行匹配.但是，如果g太大，栅格算法的计算量将会大大增加，更严重的是星点可能出现在多个栅格中，使得误匹配的概率增加.反之g减小，则每个栅格将会变大，噪声对算法的影响随之减小.然而，当g变小的时候，一个栅格中出现多颗星的概率将会升高.如果g过小，会使得星模式维数太低，达不到正常识别的要求.同理，br变大会使得算法对噪声的鲁棒性变强，但是br太大会使得近邻星出现在视场之外的几率增加，使得近邻星的选择成功率降低，这将会直接影响到算法的星图识别成功率.因此，在小视场的星敏感器使用中，需要统计星点在视场中的分布情况，然后根据统计结果来设置栅格数目g和缓冲半径br.

1.2 扩充星图法

在某些情况下为了满足低功耗、小体积的条件，星敏感器的视场一般被设置得很小，Nano-JASMINE就是一个典型实例［13］.在这种情况下，不能保证每次都能捕获到两颗以上的恒星，因此星图识别的过程就不能正常进行，下面介绍一种利用扩充星图进行星图识别的方法［8-9］，具体步骤:1)t时刻星图识别成功后，计算载体的姿态，利用姿态信息分析星图中没有被用来进行星图识别的星点，并记录它们的位置.2)利用得到的姿态信息和陀螺输出的测量信息估计t+1时刻步骤1中记录的星点的位置，如果在t+1时刻星点位置不在预测星图中，则按照图2所示的扩充星图法将视场扩充.3)当星敏感器在t+1时刻得到拍摄星图时，将其与步骤2预测星图中的星利用三角形算法进行识别，若识别成功的星点数目不小于2，利用识别成功的恒星计算载体姿态，否则跳到下一步.4)识别扩充视场中的恒星，若失败，则整个星图识别失败.

图2 扩充星图法

1.3 扩充栅格算法

上述扩充星图的方法，将星图扩充之后能够得到更丰富的星点信息.这种方法实际上跟增大星敏感器视场起到的效果相同.因此为了更加的直观，本文将其加以改变，变为扩充视场的方法，假设实际视场大小为θR×θR，扩充后的视场大小为θE×θE，算法流程见图3，算法步骤:1)t时刻星图识别成功后，计算载体的姿态.2)在t+1时刻利用得到的姿态和陀螺的输出信息计算视轴的方向矢量P.利用P从星表中选择落入视场θE×θE中的恒星，生成t+1时刻的模拟星图A.此模拟星图包括模拟真实星图和扩充星图两部分，如图4所示.3)敏感器在t+1时刻拍摄到的为星图B，将星图A和B组合并删除星图A中真实模拟星图中的星点，从而生成星图C，如图4所示.4)从星图C中的真实视场中选择待识别星，使用栅格算法进行识别.

图3 算法流程

图4 扩充栅格算法

从上述步骤可以看出，在星图识别阶段使用的是栅格算法，它的噪声鲁棒性要优于现有扩充星图法中的三角形算法.同时通过将视场进行扩充可以得到更多的星点信息，从而达到栅格算法的要求.传统栅格算法使用查找表进行星模式的查找和匹配，在参考星表较大的情况下效果很好.但是扩充栅格算法用于跟踪模式，不需要建立参考星表，因此本文用图5所示的方法构造星模式:每一个栅格分配一个数字，最后记录有伴星的栅格分配到的数字;将这些数字组成一个矢量，这个矢量就可以看作参考星的星模式.

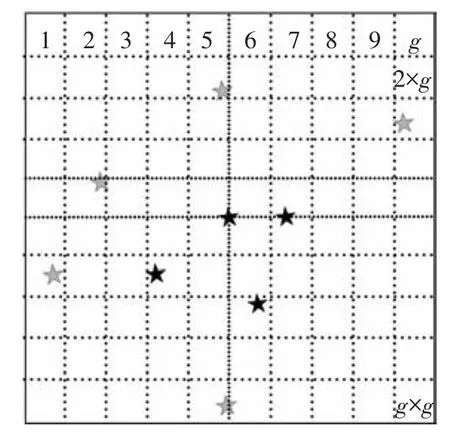
图5 星模式的构造

2 陀螺噪声分析

由于陀螺漂移的存在，使用陀螺信息生成的模拟星图中必定引入了因陀螺漂移而产生的位置噪声.研究该噪声对星图识别算法的影响是十分必要的.

为简化计算，假设星敏感器与载体之间的安装矩阵为单位阵且陀螺捷联安装在载体的三轴上.假设在t时刻，星点在像平面的位置为(xtc，.如图 6 所示，ωx、ωy、ωz分别为载体三轴的转动角速度，由ωy引起的星点移动速度为v1且沿x轴反方向;由ωx引起的星点移动速度为v2且沿y轴方向;由ωz引起的移动速度可分解为沿着x轴的负方向速度v3和沿着y轴的正方向速度v4.则星点的移动速度可以表示为［14］

式中:f为星敏感器光学系统的焦距.

根据式(1)可以得到t+δt时刻星点的位置为

当δt较小时，有

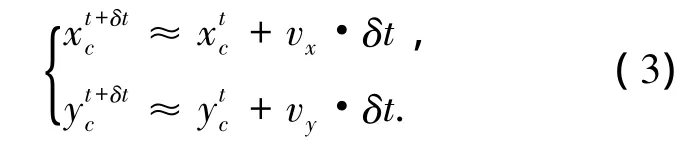
陀螺的测量模型可以简化为ω=ωr+b+η，其中ωr为真实角速度;b为陀螺常值漂移;η为陀螺随机测量噪声，将其代入上式，则得

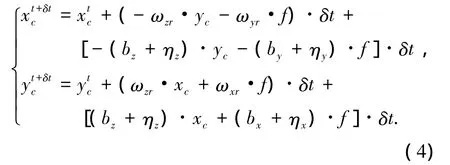
则由陀螺测量噪声引起的星点位置误差为

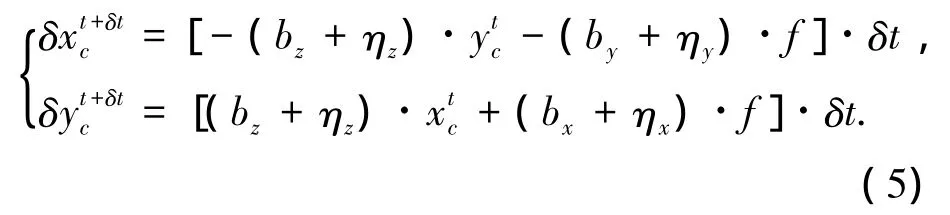
假设3个陀螺相同，bx+ηx=by+ηy=bz+ηz=b+η，那么由陀螺测量噪声引入的总的星点位置误差为

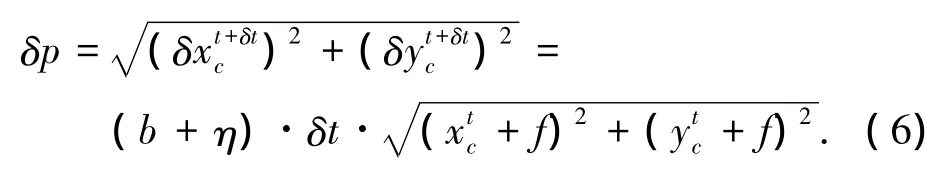
假设星敏感器误差引起的星点位置噪声为δps像素.若新方法在星点位置噪声为δp+δps时仍能保证较高的星图识别成功率，则能够说明新算法对陀螺噪声有较强的鲁棒性.

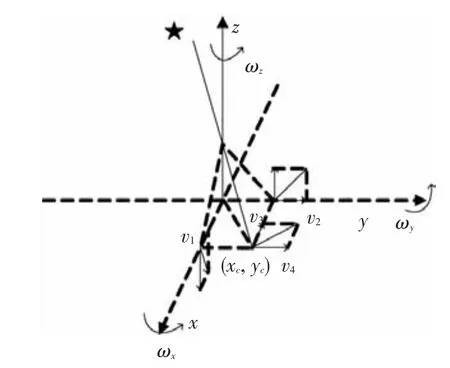
图6 星点移动示意

3 仿真与分析

仿真中所用的基本星表是第谷第二星表(Tycho-2)，从中选取星等亮度大于 8.0的星42 057颗组成导航星表.

由于各种噪声的存在，星敏感器不能够完美地呈现星空.因此，为了模拟真实情况下的星图识别过程，用两种形式的高斯白噪声对所有的噪声进行模拟.第 1种是星等噪声 MN(magnitude noise)，由恒星亮度的变化引起.第2种是星点的位置噪声PN(position noise)，由星敏感器噪声和陀螺测量噪声引起，测量单位为像素.另外，由于恒星的自行、测量误差等因素的存在，星表中也存在噪声.对于大视场星敏感器而言，与其他噪声相比星表噪声非常小，可以忽略不计.然而，对于本文使用的小视场星敏感器，星表噪声是需要考虑的一个因素，因此在本文中星表噪声也用MN和PN来表征.图7、8分别描述了星敏感器拍摄星图和扩充法中用到的模拟星图的模拟方法.

图7 拍摄星图的模拟方法

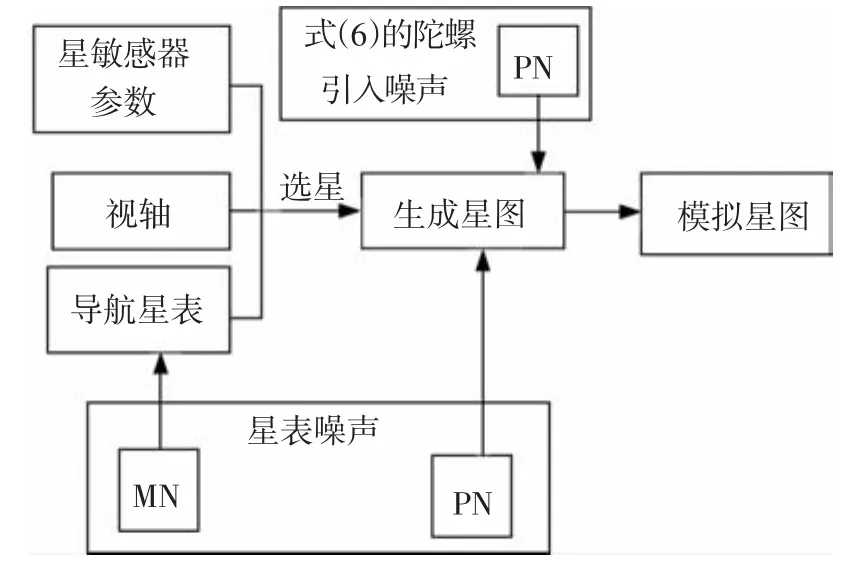
图8 模拟星图的模拟方法

3.1 仿真条件设置

根据1.1节的叙述，需要根据星点在星图中分布的统计结果来设置栅格数目g和缓冲半径br.选取星敏感器视场大小为4°×4°，星等敏感极限为7.5，图9为10 000次随机视轴指向星点之间角距分布的统计结果.

图9 视场中星点角距分布统计

根据统计结果，星点之间的角距在0～0.1°之间的概率为 0.17%，在 0.1～0.2°之间的概率为0.67%，在 0.2～0.3°之间的概率为 1.02%.则角距分布在 0～0.2°之间的概率为 0.17%+0.67%=0.84%，因此选取栅格大小为0.2°.选取扩充视场大小为 8°×8°，像平面像素为 1 024×1 024，则栅格数目g=8°/0.2°=40.同理选择缓冲半径br=0.3°，约为40像素.其他仿真参数设置:星表星等噪声为0.1像素，位置噪声为0.1像素，陀螺常值漂移为 1°/h，随机漂移为 0.5°/h.

3.2 仿真结果

本文的仿真中分为两个部分，第1部分是在不同噪声环境下本文的扩充栅格算法与现有的扩充星图法的对比，第2部分是算法性能的全面验证.

图10为星敏感器星等噪声为0.2像素时扩充栅格算法和扩充星图法的星图识别成功率随着位置噪声变化的曲线.

图10 识别成功率随位置噪声变化曲线

图11为位置噪声为0.3像素时扩充栅格算法和扩充星图法的星图识别成功率随着星等噪声变化的曲线.

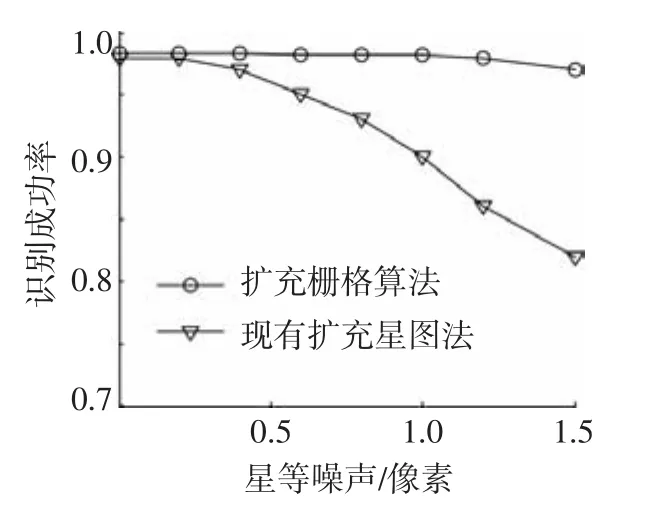
图11 识别成功率随星等噪声变化曲线

由图10、11可见，随着星等噪声和位置噪声的增加，现有的扩充星图法由于在星图识别阶段用的是三角形算法，所以其噪声鲁棒性较差，导致星图识别成功率迅速降低.而由于扩充栅格法用的是鲁棒性较强的栅格算法，其识别成功率明显优于扩充星图法.

下面对扩充栅格算法的性能进行全面的验证，一般用如下3项指标评价星图识别算法的性能:1)算法在不同噪声环境下的星图识别成功率.2)算法平均进行一次成功识别所用的时间.3)算法数据库对内存的要求.

随着微电子技术的发展，大容量小体积的存储器件不断出现，内存的需求对星图别算法的限制越来越小，因此本文不考虑这方面的因素.由于新算法用到了陀螺信息，由式(6)可知星敏感器的更新周期会影响陀螺引入的位置噪声.因此本文添加一项星敏感器更新周期对算法识别成功率的影响.首先，当星敏感器更新周期为1 s时，在10 000次随机视轴的仿真中，新算法星图识别成功率与位置噪声标准偏差之间的关系曲线见图12.

图12 星图识别成功率

由图12可见，当位置噪声小于1像素时，新算法的星图识别成功率大于97.4%.同时还注意到一点，当位置噪声为0时，星图识别成功率也达不到100%.因为有时星敏感器只能捕获到一颗或者两颗星，这时成功识别两颗星的概率会大大降低.在上述仿真条件下，10 000次随机视轴仿真中，星敏感器捕获星数目的统计结果见表1和图13.星敏感器捕获到小于两颗星的概率为0.6%，而星图识别过程成功的要求是至少成功匹配两颗星.因此即使所有误差都不存在，星图识别的成功率也只有99.4%.但是，这并不能代表本文的算法不够优秀，从表中可以发现，星敏感器捕获不小于6颗星的概率为79.71%，即传统算法即使在所有噪声都为零时，星图识别成功率也只能达到79.71%，而本文算法在位置噪声为1像素的情况下仍能够达到97.4%.能够取得这么高的成功率，除了视场扩充带来更丰富的星点信息之外，近邻星选择成功率的提高也是一个很重要的因素.传统方法近邻星的选择成功率最高只有52.2%，而本文算法近邻星成功率最大可达到86.7%，如图14所示.主要原因是，新算法的参考星是从真实星图中选择，而真实星图在整个扩充后的星图的中央，因此参考星的近邻星不会出现在扩充后星图的边缘，使得近邻星出现在星图外的概率大大降低.

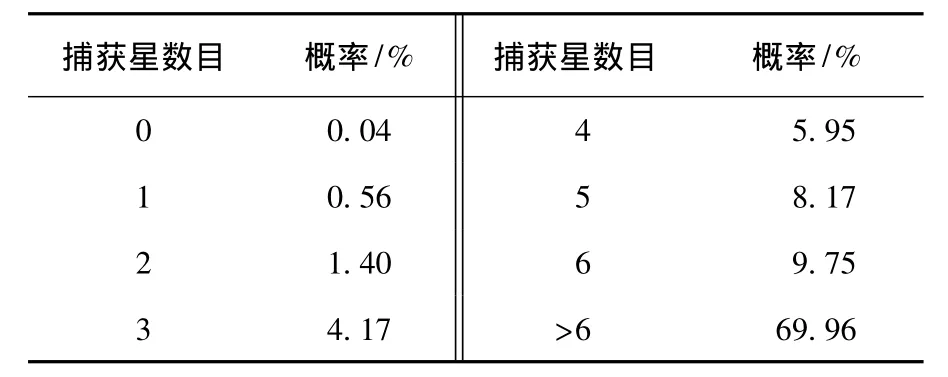
表1 星敏感器捕获星数目统计

图13 星敏感器捕获星数目的统计概率

图14 新算法近邻星选择成功率

假设星敏感器的更新周期为t，图15为当星敏感器的位置噪声为0.3像素时，更新周期与星图识别成功率的仿真结果.图16为由陀螺漂移引入的位置噪声随更新周期变化的仿真结果.

图15 更新周期对星图识别成功率的影响

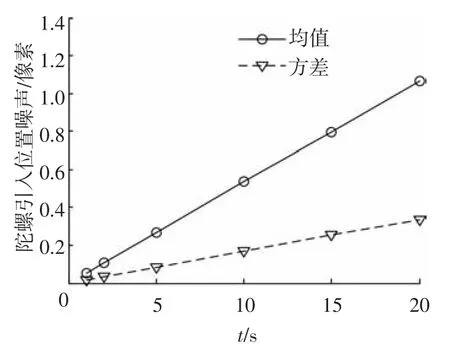
图16 陀螺引入的位置噪声与更新周期的关系曲线

由15、16可见，当星敏感器更新周期为10 s时，由陀螺漂移引入的位置噪声约为0.54像素，此时总的位置噪声为0.84像素，星图识别成功率为97.6%.而实际上星敏感器的更新频率为1～10 Hz，即其更新周期小于1 s，因此由陀螺引入的位置噪声小于0.05像素，这时总的位置噪声小于0.35像素，星图识别成功率达到98.2%.因此，考虑到栅格算法对噪声的强鲁棒性，由陀螺漂移产生的噪声对星图识别成功率的影响非常小，可以不予考虑.

图17为星敏感器捕获星数目与进行一个星图识别的平均识别时间之间的关系.仿真硬件:Pentium(R)CPU E5200，2.49 GHz，计算机系统为Windows XP，所用软件为 MATLAB，代码没有经过优化.由图中看出，随着捕获星数目的增加，星图识别所用时间也随之增加.但是由于小视场星敏感器一次只能捕获几颗星，因此平均识别时间大约为6 ms.

图17 新方法耗时

另外，本文还将新方法应用于低星等敏感极限的星敏感器时，进行仿真，得到了相似的实验结果.综上所述，扩充栅格算法的噪声鲁棒性要优于现有扩充星图法，同时能够将视场进行扩充，得到足够的星点信息来进行星图识别，且在复杂噪声环境中能够达到很高的识别成功率，是一种适用于小视场或低星等敏感极限的星敏感器的星图识别算法.

4 结 论

1)提出了一种适用于小视场或低星等敏感极限星敏感器的扩充栅格算法.该算法是基于传统高鲁棒性的栅格算法而建立的，相较于现有扩充星图法拥有更强的噪声鲁棒性.同时新算法可以通过扩充视场来获得更多的星点信息，能够打破原始栅格算法的限制.

2)实验结果表明，在星敏感器为小视场或者低星等敏感极限时，扩充栅格法的星图识别成功率优于传统的扩充星图法.扩充栅格法的近邻星识别成功率优于传统的栅格算法.综合上述优势，该扩充栅格算法在小视场星、低星等敏感极限星敏感器上体现出了较好的技术性能.

［1］LIEBE C C.Star trackers for attitude determination［J］.IEEE Trans on Aerospace and Electronic System，1995，10(6):10-16.

［2］PADGETT C，KREUTZ-DELGADO K.A grid algorithm for autonomous star identification［J］.IEEE Trans on Aerospace and Electronic System，1997，33(1):202-213.

［3］张广军.星图识别［M］.北京:国防工业出版社，2011:22-29.

［4］COLE C L.Fast star pattern recognition using spherical triangles［D］.Buffalo，NY:State University of New York at Buffalo，2004.

［5］KOSIK J.Star pattern identification aboard an inertially stabilized spacecraft［J］.Journal of Guidance，Control and Dynamics，1991，14(1):230-235.

［6］ UDOMKESMALEE S，ALEXANDER J，TOLIVAR F.Stochastic star identification ［J］.Journal of Guidance，Control and Dynamics，1994，17(6):1283-1286.

［7］PADGETT C，KREUTZ-DELGADO K，UDOMKESMALEE S.Evaluation of star identification techniques［J］.Journal of Guidance，Control and Dynamics，1997，20(2)，259-267.

［8］HO K.A survey of algorithms for star identification with low-cost star trackers ［J］.Acta Astronautica，2012，73:156-163.

［9］Compact and low-cost advanced star sensor system［R］.Tokyo，Japan:Mitsubishi Electric and Electronics，2002:1-12.

［10］HO K，NAKASUKA S.Novel star identification method combining two star trackers with extended FOVs［C］//AIAA Guidance，Navigation，and Control Conference.Toronto，Ontario，Canada:IEEE，2010:1-15.

［11］SAMAAN M A，MORTARI D，JUNKINS J L.Recursive mode star identification algorithms［J］.IEEE Trans on Aerospace and Electronic System，2005，41(4):1246-1254.

［12］MORTARI D，JUNKINS L J，SAMAAN M A.Lost-inspace pyramid algorithm for robust star pattern recognition［C］//Proceeding of Guidance and Control 2001.Colorado:Elsevier，2001:1-23.

［13］Scholarpedia.Nano-JASMINE［EB/OL］.http://www.space.t.u-tokyo.ac.jp/nanojasmine/Index-e.htm.

［14］XING Fei，CHEN Nan，YOU Zheng，et al.A novel approach based on MEMS-Gyro’s data deep coupling for determining the centroid of star spot［J］.Mathematical Problems in Engineering，2012，2012:403584.