断续电流型开关电感Buck-Boost变换器的分岔现象

孙立山，杨 爽，刘洪臣

(哈尔滨工业大学电气工程及自动化学院，150001哈尔滨)

DC-DC变换器属于强非线性系统，当电路参数发生变化时，系统将产生分岔现象并最终进入混沌状态，从而导致系统的运行状态无法预测，甚至造成系统故障.因此，深入研究DC-DC变换器的非线性行为，分析电路参数对系统动态特性的影响，对于开关变换器系统的设计具有十分重要的理论意义和应用价值.

开关电感结构是近年来提出的一种新型拓扑，具有升压模式和降压模式两种结构，可以分别嵌入到传统DC-DC变换器中，以提高系统的升压或降压能力［1-2］，因而得到国内外学者的广泛关注.

目前，国内外学者对传统DC-DC变换器中非线性行为的研究已经比较深入［3-15］，人们利用数值模拟和非线性动力学理论等方法，深入分析了系统的分岔和混沌现象.以Buck-Boost变换器为例:文献［13-15］证实了传统Buck-Boost变换器中存在边界碰撞分岔、倍周期分岔和阵发混沌等多种复杂的非线性动力学行为.然而，上述成果的研究对象均为传统Buck-Boost变换器，而对基于开关电感结构的Buck-Boost变换器(下面简称开关电感Buck-Boost变换器)中非线性行为的研究结果却未见报道.并且目前对于DC-DC变换器中非线性现象的研究主要集中于连续电流模式(CCM)，对断续电流模式(DCM)的情况则研究较少.实际上，对DCM模式下系统的非线性动力学行为进行研究具有更为广泛的意义.

因此，本文首次以开关电感Buck-Boost变换器为研究对象，深入分析了系统在DCM模式下的分岔和混沌现象.首先，从状态方程出发，建立了DCM模式下系统的离散时间映射模型，并基于此模型，绘制了不同参数范围内系统的分岔图，分析了电路参数对系统动态特性的影响;然后，采用Runge-Kutta算法直接对状态方程进行求解，得到了系统的庞加莱截面，更加直观地反映了系统的运行状态;接下来，根据系统不动点邻域内Jacobian矩阵特征值的变化趋势确定系统首次分岔点的位置;最后，应用PSIM软件搭建符合实际运行条件的仿真模型，通过时域波形图和相轨图观察变换器丰富的动力学演化过程，验证了离散时间模型的正确性.

1 变换器的工作原理与建模

1.1 工作原理与状态方程的求解

开关电感Buck-Boost变换器是运用开关电感结构代替传统Buck-Boost变换器中原有的储能电感而形成的，电流模式控制下系统的电路原理图如图1所示.由图1可知，该系统是由两个电感和一个电容组成的三阶电路.电路的工作原理如下:将电感L1的电流iL1与参考电流Ⅰref比较的结果作为RS触发器R端的输入，时钟信号通过触发器的S端输入，触发器的Q端控制开关管S的通断.当变换器工作于DCM模式时，电路有以下3种模态，如图2所示.

图1 电流模式控制下的开关电感Buck-Boost变换器

图2 DCM运行时的模态

模态1.开关管S导通，二极管D0、D12截止，D1、D2导通，电感L1、L2并联充电，电容C向负载提供能量，其等效电路如图2(a)所示，此时有

模态2.开关管S截止，二极管D0、D12导通，D1、D2截止，电感L1、L2串联为电容C充电，并向负载提供能量，其等效电路如图2(b)所示，此时有

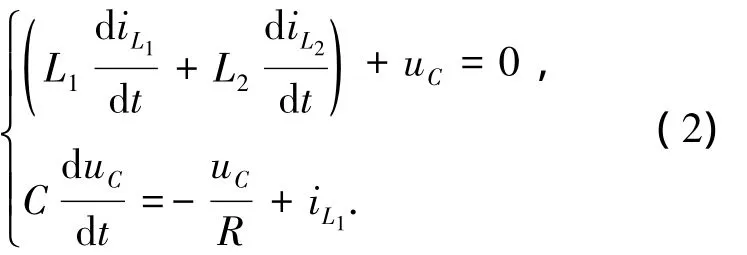
模态 3.开关管S、二极管D0、D1、D2、D12均截止，只有电容C向负载提供能量，其等效电路如图2(c)所示，此时有

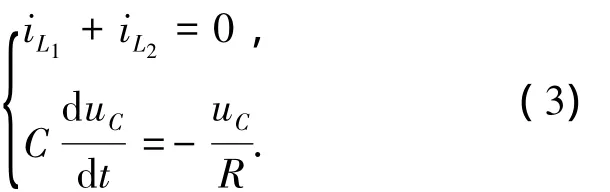
为便于分析，本文取L1=L2，则在上述3种模态中，可近似认为iL1=iL2，系统可简化为二阶模型，以电感电流iL1和电容电压uC为分析对象，则对于模态1，有

设电感电流iL1和电容电压uC的初值分别为iL1，n和uC，n，则上述方程的时域解为

设变换器工作于模态1的时间为t1，则由式(5)得

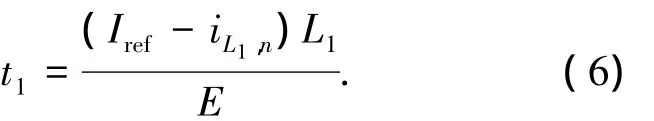
同理，模态2的微分方程可以简化为

由式(5)可以解得

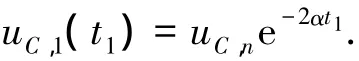
设变换器工作于模态 2的时间为t2，则iL1，2(t2)=0，由(8)式可得

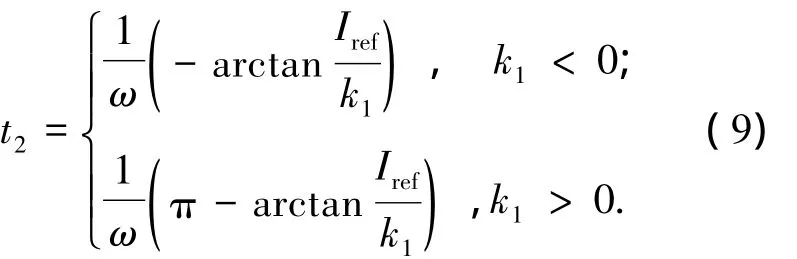
当变换器工作于模态3时，简化的微分方程为

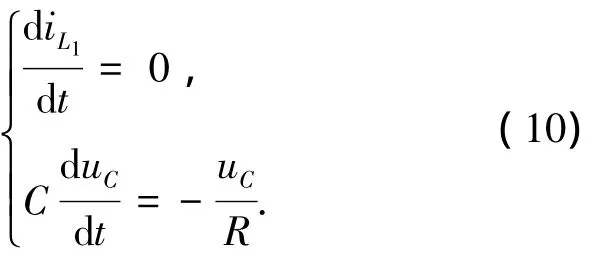
状态方程(10)的解可表示为

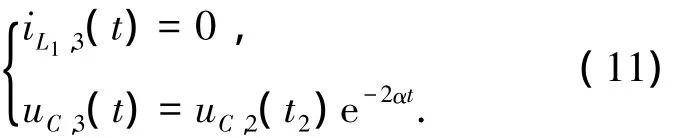
其中:uC，2(t2)=e-αt2(uC，1(t1)cos ωt2+k2sin ωt2)．

1.2 离散时间映射模型

本文采用频闪映射的方法，设数据采样周期为T，则在相邻的采样时刻内，DCM模式下的开关电感Buck-Boost变换器有以下3种运行轨道.

当t1≥T时，在1个采样周期内，变换器只工作于模态1，则在第n个采样周期结束时，简化的微分方程对应的离散映射模型为

当t1＜T，但t1+t2≥T时，在1个采样周期内，变换器工作于模态1和模态2，则在第n个采样周期结束时，简化的微分方程对应的离散映射模型为

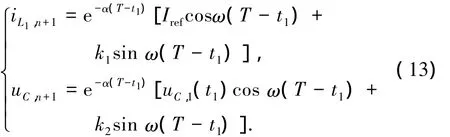
当t1＜T，且t1+t2＜T时，在1个采样周期内，变换器工作于3种工作模态，则在第n个采样周期结束时，简化的微分方程对应的离散映射模型为

式(12)～(14)即为DCM模式下，开关电感Buck-Boost变换器的离散时间映射模型.

2 变换器的动力学行为分析

2.1 分岔图

在动力学系统中，当系统参数的变化超过某临界值时，系统的定性形态会突然发生变化，这种现象叫做分岔，临界值即为分岔点.通过分岔图可以清楚地知道系统在不同参数下的稳定性，因此，分岔理论是研究系统稳定性的有力工具.

在绘制分岔图前，首先给出电感电流边界的定义.当开关电感Buck-Boost变换器工作于DCM模式时，在状态空间中存在两个电流边界，设第1个电流边界为Ⅰb1，它满足如下关系:以Ⅰb1为电流初值，经1个开关周期T后电感电流iL1恰好到达参考电流Ⅰref;设第2个电流边界为Ⅰb2，它满足:以Ⅰb2为电流初值，经1个开关周期T后电感电流iL1恰好为0，则此阶段电感电流iL1到达参考电流Ⅰref的时间为T-t2，则由式(5)可知，DCM模式下开关电感Buck-Boost变换器的两个电感电流边界可分别表示为

选取电路参数为C=10 μF，R=10 Ω，T=100 μs和L1=L2=0.1 mH，固定E=6 V，以参考电流Ⅰref为分岔参数，基于1.2节所导出的离散映射模型，对系统进行数值模拟，得到电感iL1随参考电流变化的分岔图，如图3所示，其中红色的点划线表示第1个电感电流边界Ⅰb1，绿色的点划线表示第2个电感电流边界Ⅰb2．由图3可知，当参考电流Ⅰref达到2.5 A左右时，分岔轨线与边界Ⅰb2发生碰撞，系统的工作状态由周期1经边界碰撞分岔变为周期2，随着参考电流的进一步增大，电感电流并非完全工作在不连续状态，而是在某些时钟周期内有不连续现象;当Ⅰref为7.5 A左右时，系统再次发生边界碰撞分岔变为周期4，而后激变进入混沌状态．然而，这个混沌状态并没有被保持，当Ⅰref＞9.5 A时，混沌态和周期态交替出现，系统发生了DCM阵发混沌，阵发混沌前的分岔为切分岔.

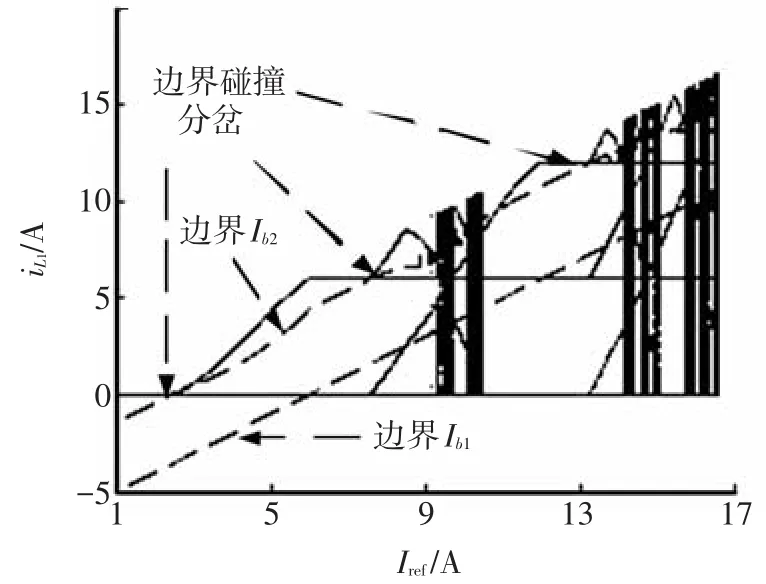
图3 Ⅰref为参数的分岔

固定Ⅰref=2 A，其他电路参数与前者相同，以输入电压E为分岔参数，通过数值模拟得到的分岔图如图4所示．由图4可知，随着输入电压E的减小，系统的工作状态也是由周期1经边界碰撞分岔变为周期2，再到周期4，然后进入DCM阵发混沌区，并存在明显的周期窗口.可见，其通往混沌的道路与参考电流变化时相同，但参数变化的方向相反.

值得注意的是，边界碰撞分岔虽然也能引发倍周期现象，但与倍周期分岔有本质的区别.发生倍周期分岔时，分岔点附近的倍周期轨道与分岔发生之前的周期轨道是近似垂直的;而在边界碰撞分岔中，二者并不垂直.并且由图3和图4还可以看出，当变换器工作于DCM模式时，引发系统不稳定的因素主要是电流边界Ⅰb2，当系统轨线与Ⅰb2发生碰撞时，随即产生分岔现象，并最终进入混沌状态;然而，当系统轨线与Ⅰb1发生碰撞时，并未出现分岔，而仅仅改变了轨线的路径，故Ⅰb1对系统的稳定性影响相对较小．

图4 E为参数的分岔

2.2 庞加莱截面

在相空间中选取1个既不与轨线相切，又不包含轨线的截面，即庞加莱截面，轨线与庞加莱截面的交点称为截点.由非线性动力学理论可知，通过观察截点的情况便可以判断是否发生混沌:当截面上只有1个点或少数离散点时，运动是周期的，点的个数代表状态的周期数;当截点形成1条闭合的曲线时，运动是准周期的;当截点连成片或具有分形结构时，系统便处于混沌状态.

为证明随着参考电流Ⅰref的增大，变换器确实存在图3分岔图所体现的丰富的非线性行为，本节从不同工作模态下的状态方程出发，采用Runge-Kutta算法直接对每个开关周期内的微分方程进行求解，得到开关电感Buck-Boost变换器在典型参考电流值下的庞加莱截面，其结果如图5所示.

图5 不同参考电流下的庞加莱截面

由图5(a)～5(c)可以清楚的知道，当参考电流分别为1、5、8 A时，庞加莱截面上的点是离散的，根据点的个数可知，变换器先后工作于周期1、周期2和周期4;图5(d)和5(f)中的截点在某些区域已经连成片，说明当参考电流为9.5、15 A时，变换器工作于混沌状态;图5(e)体现了当参考电流为11 A时，即在阵发混沌中，存在明显的周期3窗口.上述结果与图3所示分岔图中各点呈现的状态一致，验证了离散映射模型的正确性，并且更加直观地反映了参考电流取不同值时变换器所处的工作状态.

3 基于离散时间模型的稳定性分析

3.1 不动点及Jacobian矩阵

令xn+1=xn=x*可求出系统的不动点x*，开关电感Buck-Boost变换器基于简化状态方程的离散时间模型在不动点邻域内的Jacobian矩阵可表示为

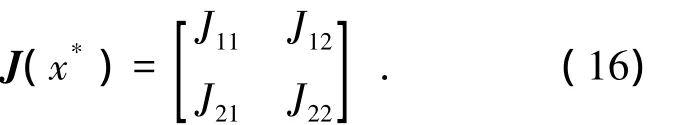
式(16)的特征方程为

根据1.2节可知，在相邻的采样时刻nT和(n+1)T内，DCM模式下的开关电感Buck-Boost变换器有3种运行轨道，可分别对其稳定性进行分析.

当t1≥T时，式(12)所表示的离散系统不存在不动点，其Jacobian矩阵的元素分别为

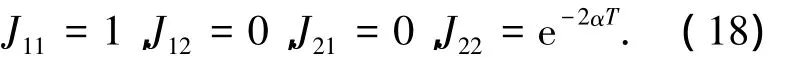
其特征多项式为

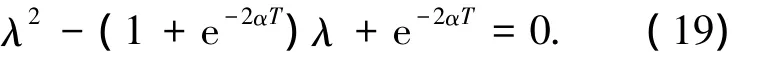
解得 λ1=1，λ2=e-2αT，此时离散系统Jacobian矩阵的特征值有两个正实根，并且其中一个为1.

当t1＜T，但t1+t2≥T时，将xn+1=xn=x*代入式(13)，可求得系统的不动点，且由式(13)可求得其Jacobian矩阵的元素分别为

其特征多项式为

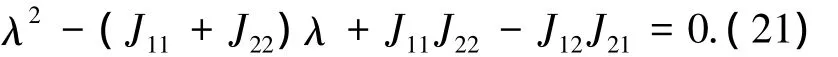
解得

此时离散系统的Jacobian矩阵有两个非零特征根.

当t1＜T，且t1+t2＜T时，式(14)所表示的离散系统仅存在1个不动点，由式(14)求得其Jacobian矩阵的元素分别为

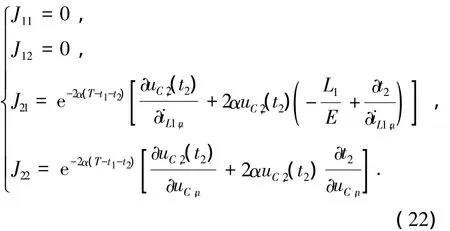
其中:

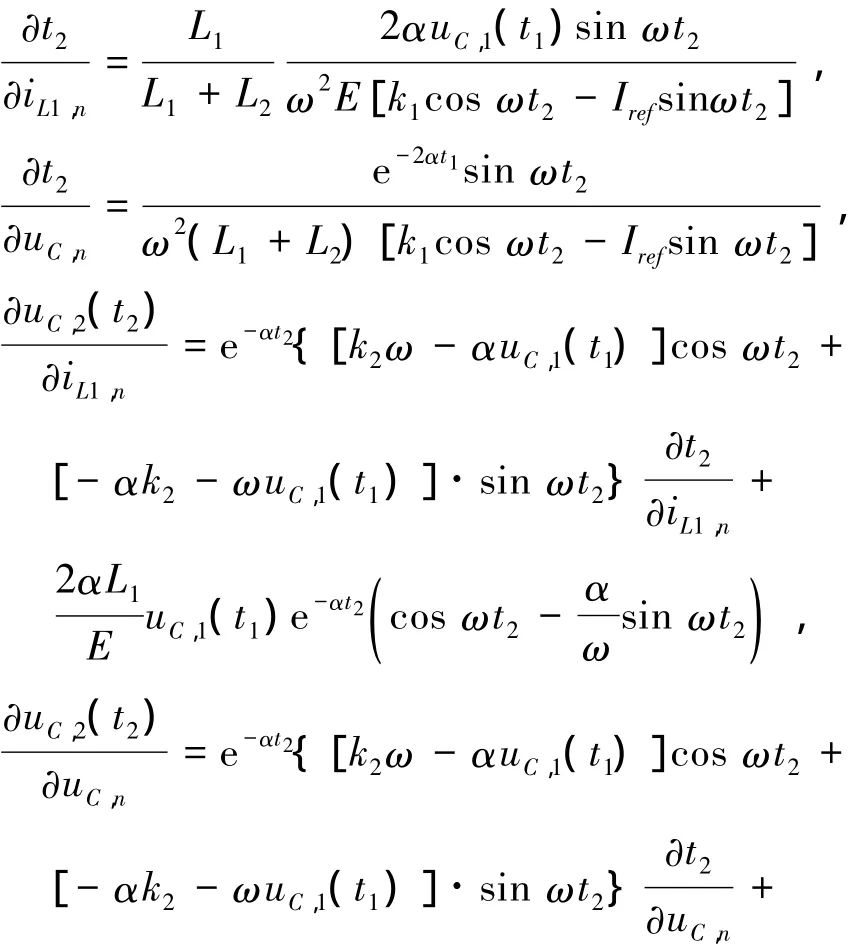
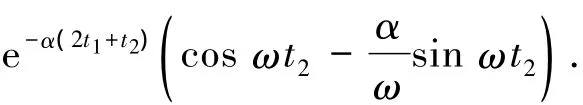
其特征多项式为

解得 λ1=J22，λ2=0，此时离散系统的Jacobian矩阵总有1个零特征根和1个非零特征根.

3.2 Jacobian矩阵的特征乘子

根据以上分析，本节计算了发生分岔前后离散映射模型在不动点邻域内的Jacobian矩阵的特征值.表1、2分别给出了不同参考电流和不同输入电压下系统Jacobian矩阵特征值的变化情况.由表1可知，参考电流在(2.44 A，2.505 A)时，随着参考电流的增大，周期1轨道的特征值由(-0.022 6，0)跃变为(-1.003 8，0.173 0).由表2可知，输入电压在(4.8 V，4.95 V)时，随着输入电压的减小，周期1轨道的特征值由(-0.026 6，0)跃变为(-1.000 1，0.172 5).由此可知，系统发生了边界碰撞分岔，且首次分岔的位置分别在Ⅰref=2.505 A和E=4.8 V处，这与图3、4所示的分岔图结果相一致.

表1 不同参考电流下系统Jacobian矩阵的特征值

表2 不同输入电压下系统Jacobian矩阵的特征值

4 PSIM验证

PSIM软件是一款针对电力电子和电机控制的仿真软件［13］，因仿真速度快、操作简单而得到了广泛的应用.为进一步验证离散模型的正确性，本章根据图1所示原理图，在PSIM软件中搭建了系统的仿真模型.选取参考电流Ⅰref为变量，其他电路参数与绘制图3所示分岔图时所选取的参数一致，典型参考电流值下的仿真结果如图6～9所示.

由图6～8可知，当参考电流分别为1、5、8 A时，变换器分别工作于周期1、周期2和周期4，时域波形表现为相应的周期性，相轨图则由有限个数的封闭曲线组成，且由iL1的时域波形图可以看出，在上述电路参数下，变换器确实工作于DCM模式.图9给出了参考电流为9.5 A时的时域波形图和相轨图，此时变换器工作于混沌状态，时域波形因失去周期性而显得杂乱无章，各个开关周期下的幅值跳跃较大，表明混沌状态是不稳定的，有害的;相轨图则由一定区域内随机分布的轨线组成.由仿真结果不难看出，通过PSIM仿真平台得到的时域波形图和相轨图所观察到的现象与基于离散映射模型绘制的分岔图所描述的运行状态完全一致的，证实了离散模型的正确性.

图6 Ⅰref＝1 A时iL1的时域波形图和相轨图

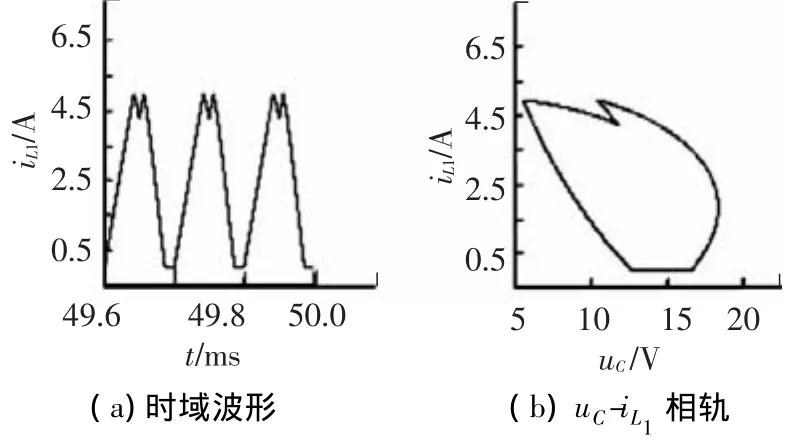
图7 Ⅰref＝5 A时iL1的时域波形图和相轨图

图8 Ⅰref＝8 A时iL的时域波形图和相轨图

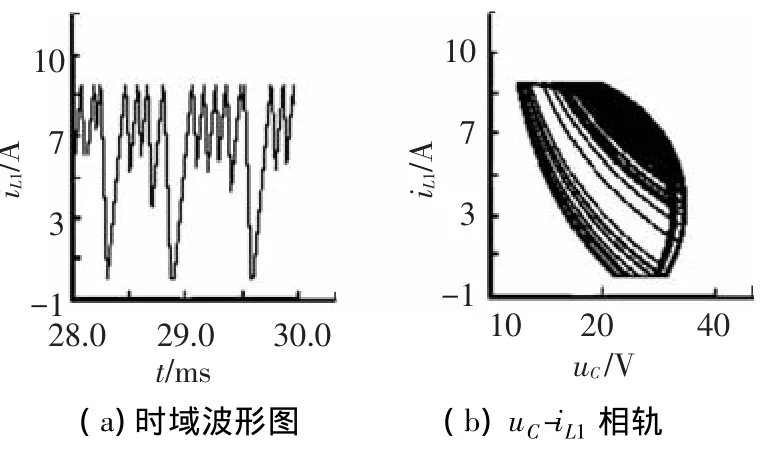
图9 Ⅰref＝9.5 A时iL1的时域波形图和相轨图

5 结 论

1)基于开关电感结构的Buck-Boost变换器虽然在一定程度上提高了传统Buck-Boost变换器的升/降压能力，但却增加了电路的阶数，使变换器的运行状态更容易受到电路参数变化的影响.

2)研究了此新型拓扑结构的变换器在DCM模式下的非线性行为，在分析电路工作原理的基础上，建立了系统的离散映射模型，并基于此模型绘制了不同参数变化下的分岔图，发现随着电路参数的变化，系统经边界碰撞分岔最终进入DCM阵发混沌状态.然后通过庞加莱截面更加直观地反映了不同电路参数下系统的周期态与混沌态，并采用Jacobian矩阵特征乘子的方法确定了首次分岔点的位置和分岔的类型.最后，在PSIM平台下搭建了符合实际运行条件的仿真模型，通过时域图和相轨图观察变换器在不同参数变化下丰富的动力学演化过程，进一步证明了离散映射模型的正确性.

3)由分岔图得出当开关电感Buck-Boost变换器工作于DCM模式下时，其工作状态主要受电流边界Ⅰb2的影响，电流边界Ⅰb1对系统稳定性的影响相对较小．

4)基于开关电感结构的Buck-Boost变换器属于强非线性系统，在设计过程中应选取合适的参数，以确保电路运行在稳定状态.

［1］AXELROD B，BERKOVICH Y，IOINOVICI A.Switchedcapacitor/switched-inductor structures for getting transformerless hybrid DC-DC PWM converters［J］.IEEE Transactions on Circuits and Systems I，2008，55(2):687-696.

［2］AXELROD B，BERKOVICH Y，IOINOVICI A.Switchedcapacitor(SC)switched-inductor(SL)structures for getting hybrid step-down Cuk/Zeta/Sepic converters［C］//Proceedings of the International Symposium on Circuits and Systems(ISCS).Kos Island，Greece:IEEE，2006:5063-5066.

［3］王诗兵，周宇飞，陈军宁，等.高阶开关功率变换器中的间歇现象［J］.中国电机工程学报，2008，28(12):26-31.

［4］LIU Fang.Intermittency and bifurcation in SEPICs under voltage-mode control［J］.Chinese Physics B，2010，19(8):205-215.

［5］LIU Fang.Fast-scale border collision bifurcation in SEPIC power factor pre-regulators［J］.Chinese Physics B，2008，17(7):2394-2404.

［6］IU H H C，TSE C K.A study of synchronization in chaotic autonomous Cuk DC/DC converter［J］.IEEE Transactions on Circuits and Systems I，2000，47(6):913-918.

［7］刘芳，张浩，马西奎.电流型单端初级电感变换器中分岔行为与稳定性［J］.电工技术学报，2007，22(9):86-92.

［8］李冠林，李春阳，陈希有，等.电流模式SEPIC变换器倍周期分岔现象研究［J］.物理学报，2012，61(17):170506.

［9］AROUDI A E，LEYVA R.Quasi-periodic route to chaos in PWM voltage-controlled DC-DC boost converter［J］.IEEE Transactions on Circuits and Systems I，2001，48(8):967-978.

［10］CHEN Yanfeng，TSE C K，QIU Shuisheng，et al.Coexisting fast-scale and slow-scale instability in current-mode controlled DC/DC converters:analysis，simulation and experimental results ［J］. IEEE Transactions on Circuits and Systems I，2008，55(10):3335-3348.

［11］BASAK B，PARUI S.Exploration of bifurcation and chaos in buck converter supplied from a rectifier［J］.IEEE Transactions on Power Electronics，2010，25(6):1556-1564.

［12］MAITY S，TRIPATHY D，BHATTACHARYA T K，et al.Bifurcation analysis of PWM-1 voltage-modecontrolled buck converter using the exact discrete model［J］.IEEE Transactions on Circuits and Systems I，2007，54(5):1120-1130.

［13］BAO Bocheng，XU Jianping，LIU Zhong.Mode shift and stability control of a current mode controlled buckboost converter operating in discontinuous conduction mode with ramp compensation ［J］.Chinese Physics B，2009，18(11):4742-4747.

［14］WU Jie， LIU Mingjian， YANG Ping.Study of bifurcation and chaos in the current-mode controlled buck-boostDC-DC converter(I):modelingand simulation［J］.Control Theory and Applications，2002，19(3):387-394.

［15］包伯成，杨平，马正华，等.电路宽范围变化时电流控制开关变换器的动力学研究［J］.物理学报，2012，61(22):220502.