考虑禁飞圆的高超声速飞行器再入预测制导

王 青，莫华东，吴振东，董朝阳

(1.北京航空航天大学 自动化学院，100191北京;2.北京航空航天大学 航空科学与工程学院，100191北京)

再入制导是高超声速飞行器再入关键技术之一，制导方法要考虑到飞行器长时间在临近空间高超声速飞行，经历的气动力热环境极其恶劣，必须对飞行轨迹进行约束以保证机体安全，还要满足速度、位置和角度等终端约束.而在接近目标区域的飞行末段，飞行轨迹变得较为平缓，且速度和高度均已大幅降低，容易被防御方拦截，为实现威胁规避或绕过敏感空间，需要制导方法具有引导飞行器规避禁飞圆的能力.

再入制导中的预测制导［1］对初始误差不敏感，落点精度较高，不依赖于标准轨迹，自适应性好，随着计算机水平的提高，越来越受到关注［2-5］.文献［2-3］解决了难以直接考虑的过程约束问题，文献［4］将人工智能控制器应用到预测制导，文献［5］基于最优化理论进一步降低了落点误差.对于再入规避技术研究，文献［6］基于伪谱法，将规避禁飞圆的再入轨迹设计问题转换为非线性规划问题求解，但算法实现较为复杂.文献［7］提出了轨迹分段优化策略，能较快设计出满足禁飞圆等约束条件的飞行轨迹，但缺乏自适应能力.文献［8］针对规避禁飞圆的滑翔再入问题提出了一种机动弹道与气动特性参数耦合设计方法.

本文综合预测制导方法和规避禁飞圆技术，针对高超声速飞行器再入，提出一种规避禁飞圆的预测校正制导方法，分别在纵向和侧向运动平面设计制导律.纵向制导利用拟平衡滑翔的优良特性，将过程约束转换成倾侧角约束，结合数值预测校正方法获取倾侧角大小;侧向制导将禁飞圆的区域约束实时转化为飞行器航向角约束，运用航向角偏差走廊动态补偿策略，形成新的偏差走廊来控制侧倾角符号，从而导引飞行器规避禁飞圆.最后对制导方法进行了仿真.

1 再入制导问题

1.1 无量纲再入运动数学模型

考虑地球为旋转圆球时，高超声速飞行器滑翔再入的三自由度无量纲运动方程组［9］为

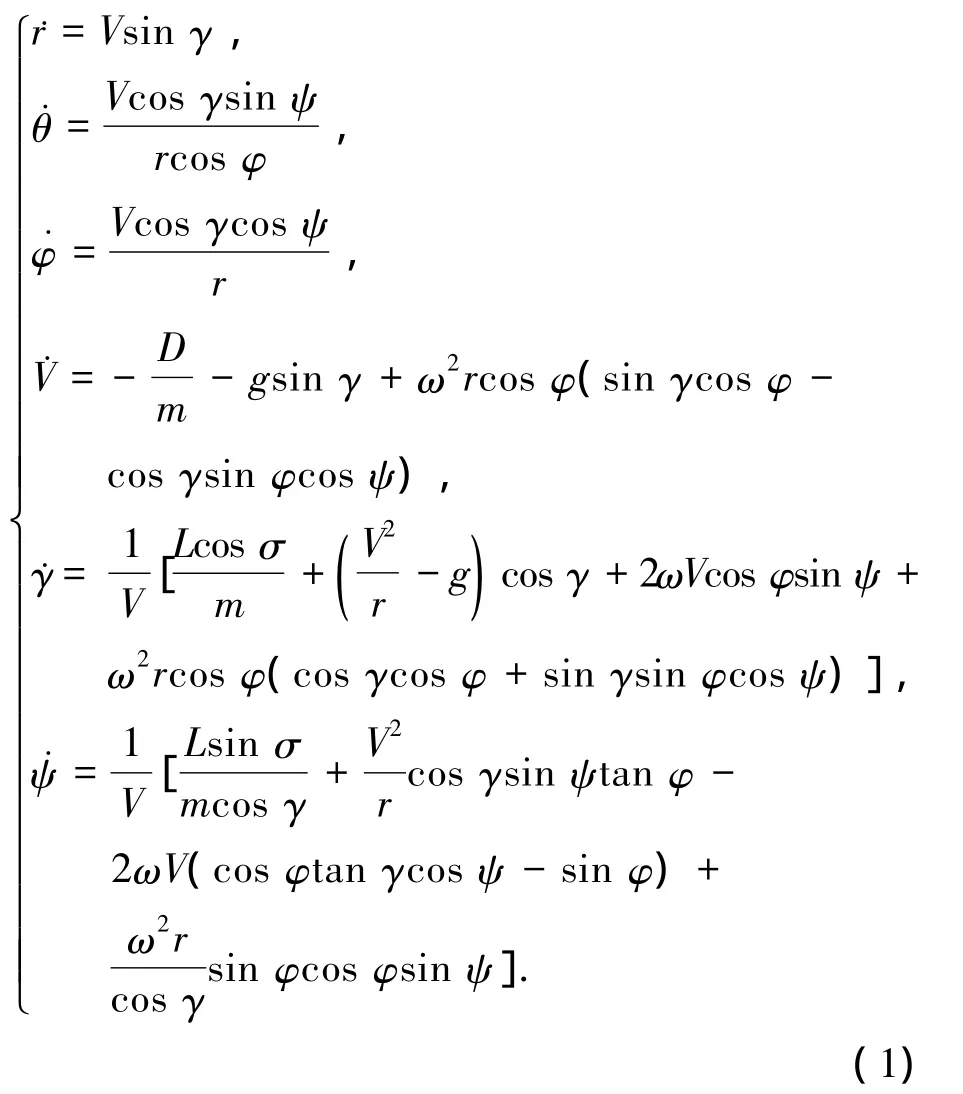
式中:无量纲地心距r、速度V、时间τ和地球自转角速度ω的无量纲参数分别为和，其中R0为地球平均半径，g0为海平面的引力加速度;θ、φ、γ和ψ分别为经度、纬度、航迹角和航向角;L、D分别为无量纲的升力加速度和阻力加速度，，其中ρ为飞行器所在位置的大气密度为飞行器的参考面积，m为飞行器质量，CL、CD分别为升力系数和阻力系数.

1.2 再入约束

再入约束包括过程约束、禁飞圆约束和终端约束.过程约束主要指为确保机体安全必须满足的热流密度约束、过载约束、动压约束和防止弹道振荡的拟平衡滑翔约束，其数学表达式分别为

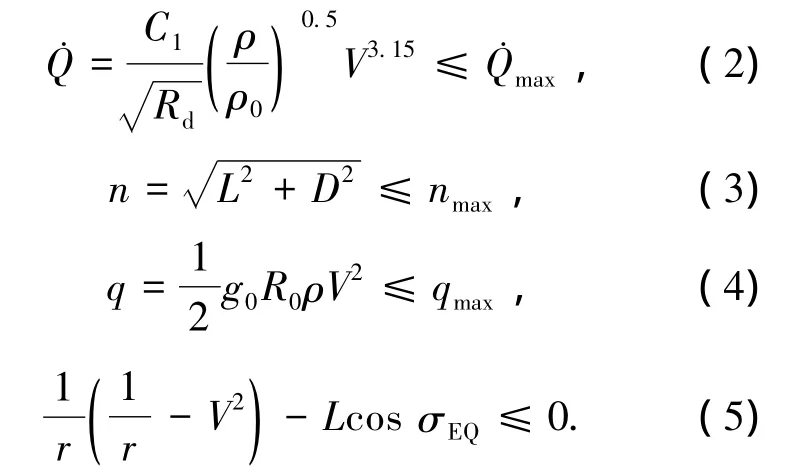
式中:C1为与飞行器相关的常数，Rd为鼻锥驻点区曲率半径，ρ0为海平面处标准大气压，σEQ为平衡滑翔边界对应的倾侧角.

禁飞圆约束指飞行器飞行过程中不允许经过的区域约束，包括地缘政治不允许通过的区域、防御方防空区域和试验飞行要规避以确保安全的区域等，本文以地球球面的圆形区域表示.

终端约束可包括速度、能量、位置和角度等，即

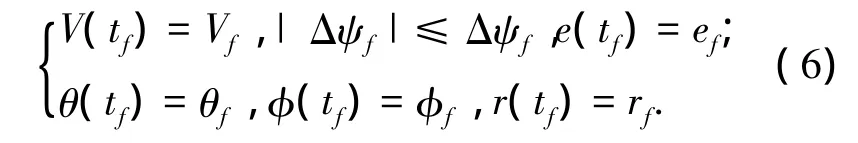
式中:e能量参数，e=1/r-V2/2.

运动方程组(1)的两个控制量为(α，σ)，当攻角由攻角-马赫数函数确定，则方程唯一的控制量是倾侧角.问题可描述为寻找适当的倾侧角，使再入飞行器从再入点飞行至目标点，且满足过程约束、禁飞圆约束及终端约束.

2 纵向制导

2.1 再入走廊的建立及转换

由过程约束建立高度-速度再入走廊，将指数大气模型ρ=ρ0e-βH(其中β为常数，H为距海平面高度)，代入式(2)～(5)，解得再入走廊边界数学模型为

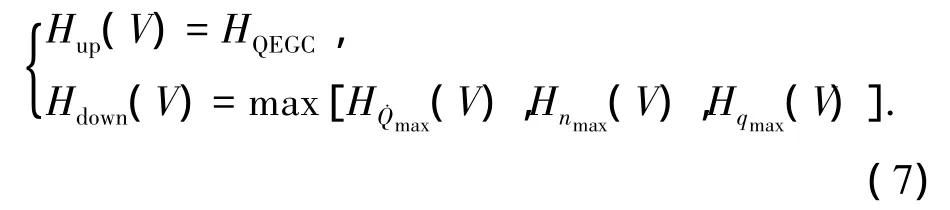
利用拟平衡滑翔条件(QEGC)得

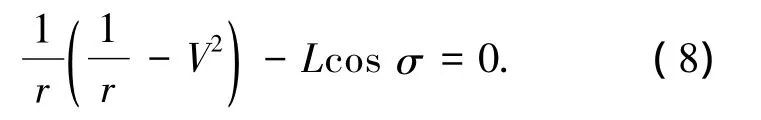
将再入走廊约束转换为控制变量约束.给定速度V，由再入走廊边界式(7)得到(rup，rdown)，分别代入式(8)可得倾侧角的边界值(|σ|min，|σ|max)，即

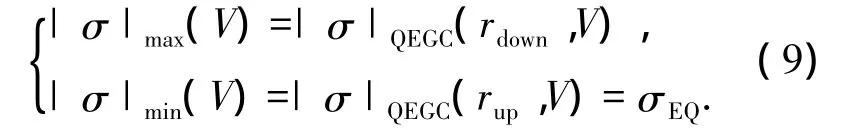
从而过程约束可由倾侧角的约束间接施加，即

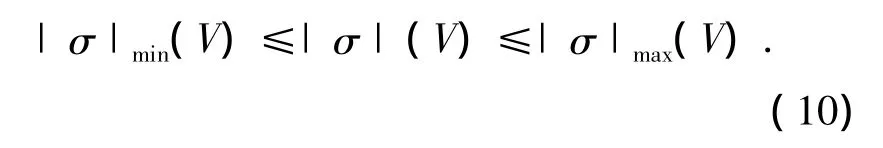
2.2 初始下降段制导

再入初始高度较高，大气稀薄使飞行器所受到的气动力很小，QEGC无法满足，故引入初始下降段，主要采用开环制导方式，以常值倾侧角σ0飞行，σ0数值通过迭代求解得到，迭代准则使轨迹在再入走廊内平滑切换到拟平衡滑翔阶段，即满足下式［10］.

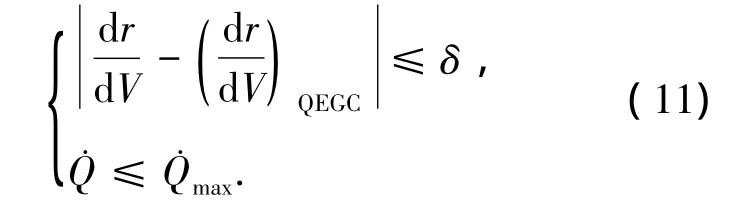
由运动方程组(1)并忽略地球旋转得

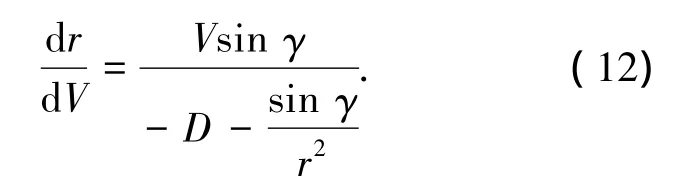
将式(9)中r看作V的函数，求r对V的导数，得因为随着σ0的增加，热流密度峰值也变大，故由式(11)对σ0的最大值进行限制.σ0符号由侧向制导确定.

2.3 拟平衡滑翔段制导

拟平衡滑翔段是主要飞行段和制导段，采用数值预测校正制导.以待飞航程偏差为目标函数，即

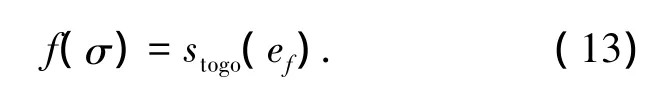
对待飞航程stogo微分，有

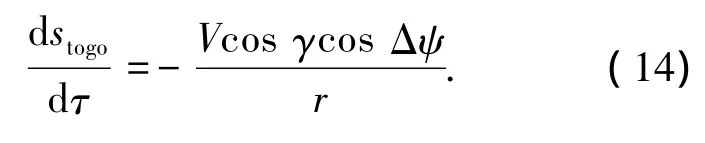
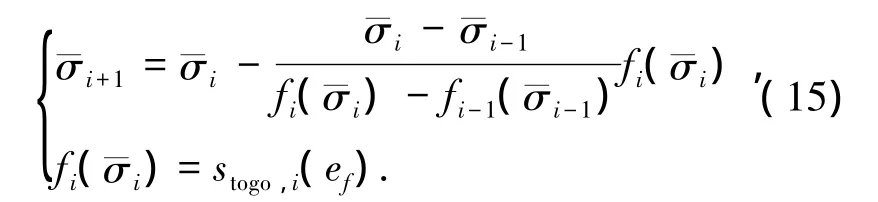
迭代得到的侧倾角数值还要满足式(10)的约束，侧倾角符号由侧向制导确定.确定所需侧倾角后，保持该侧倾角飞行，直到下一个制导周期重新进行迭代.

3 侧向制导

3.1 考虑禁飞圆的侧向制导

将禁飞圆区域约束转化为再入飞行器航向角约束，并与未考虑禁飞圆的航向角偏差(航向角与视线角之差)走廊综合，形成新的偏差走廊来导引飞行器规避禁飞圆.以飞行器向东运动，从南边绕过禁飞圆为例进行说明，其他情况同理.相关参数如图1所示，其中M为飞行器当前位置;T为目标点位置;C为禁飞圆圆心;RC为禁飞圆半径;stogo、sC分别为飞行器到目标点、禁飞圆圆心的大圆弧长;ME和MF均为未考虑禁飞圆时航向角最大偏差线，MP和MQ分别为飞行器和禁飞圆的两条切线.

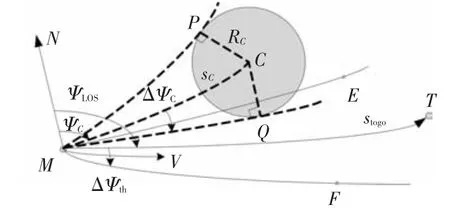
图1 考虑禁飞圆约束的侧向制导示意

在地心球面固连坐标系建立制导参数的球面几何关系，角ψLOS、ψC分别为飞行器到目标、禁飞圆圆心的视线角.

未考虑禁飞圆约束的航向角区间为

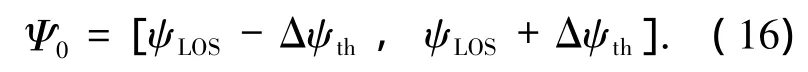
式中:Δψth为航向角偏差门槛值.

为确保绕过禁飞圆C，飞行器航向角必须偏离ψC一定角度，由图1可见，最小偏离角度为∠CMQ，表示为 ΔψC，计算公式为

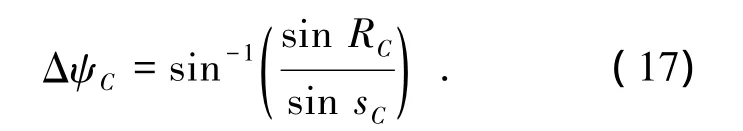
式中:弧长sC可由飞行器当前点(θ1，φ1)和禁飞圆圆心(θC，φC)计算.

由ψC和ΔψC可得到，为规避禁飞圆C而禁止进入的航向角区间为

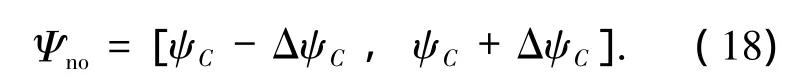
从而将禁飞圆的区域约束转换成航向角约束.由区间Ψ0综合Ψno得到考虑禁飞圆C的航向角区间为

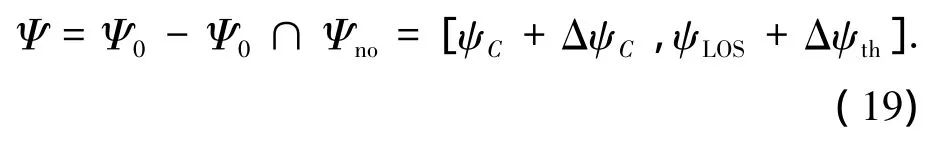
对应的航向角偏差走廊为

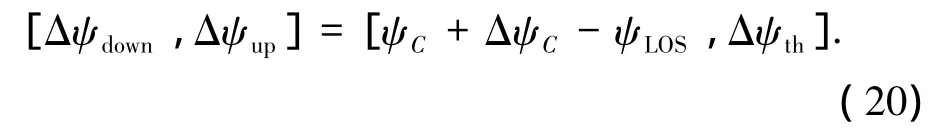
侧向制导逻辑是:当航向偏差超出走廊上边界，倾侧角符号为负;当航向偏差超出走廊下边界，倾侧角符号为正;当航向角偏差位于偏差走廊内，倾侧角符号保持不变.制导逻辑数学表达为

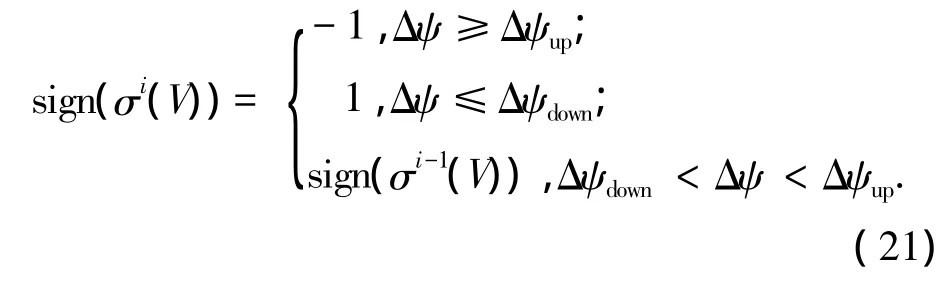
再入过程中，实时生成航向角区间Ψ控制飞行器侧向运动以规避禁飞圆，若航向角区间Ψ0和Ψno没有交集，则采用无禁飞圆约束的航向角偏差走廊.

需要说明的是，传统的再入飞行器侧向制导采用航向角偏差走廊进行控制［1，4］，将航向角偏差控制在偏差走廊内.航向角偏差走廊一般为漏斗形的速度函数，使再入飞行器具有一定机动性，也可控制侧向误差.当对再入飞行器有规避禁飞区的高机动性要求时，这种制导方法不能完全适用.

3.2 航向角偏差走廊动态补偿策略

在禁飞圆约束下，飞行器的航向角偏差走廊显然变小，过小的走廊会限制侧向机动范围，不利于规避禁飞圆，还会引起倾侧角频繁的翻转，这是飞行中应该避免的情况.

设计航向角偏差走廊动态补偿策略，在飞行过程中当走廊过小时适当进行补偿，以确保侧向机动范围并避免倾侧角频繁翻转.如图2所示，不考虑禁飞圆时，航向角范围大小由夹角∠EMF表示;考虑禁飞圆约束时，航向角范围大小由夹角∠QMF表示，∠QMF=∠EMF-∠EMQ，∠EMQ为禁飞圆C产生的约束，当∠EMQ较大时，航向角范围较小.此时补偿MF一侧，使航向角范围由夹角∠QMF补偿β至∠QMF'.

在整个飞行过程中，当航向角范围减小到某个数值时就对其进行补偿，从而实现了整个偏差走廊的动态补偿.补偿值应在合理范围内，对于不同的禁飞圆和飞行器初末位置关系，可通过多次仿真确定补偿值，以确保最终的制导精度.若原偏差走廊已经宽度合适，也可不进行补偿.仿真表明，在飞行器逐渐绕过禁飞圆的同时，航向角偏差也逐渐回归无禁飞圆的航向角偏差走廊，故可对轨迹侧向误差进行有效的限制.

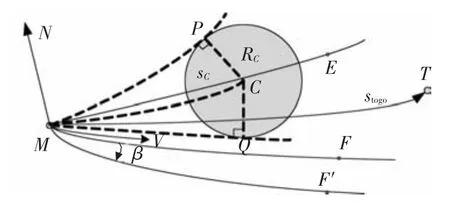
图2 航向角偏差走廊实时补偿策略示意

4 仿真及分析

以远程高超声速再入滑翔飞行器CAV-L为仿真对象，飞行器特征参数:质量为907 kg，气动参考面积为 0.35 m2，端头半径Rd=0.1 m，C1=11 030，最大升阻比为2.4.驻点热流密度、动压和过载约束分别为1 000 kW·m-2、400 kPa和4 g.给定终端速度为1 800 m·s-1，高度为20 km，经纬度(260°，40°)，速度误差＜100 m·s-1，高度误差＜2 km，位置误差(实际落点与目标点水平距离)＞20 km.

4.1 标准条件下制导方法性能仿真

为验证制导方法的有效性，考虑两种不同再入点情况，计算4个算例，再入初始条件见表1.

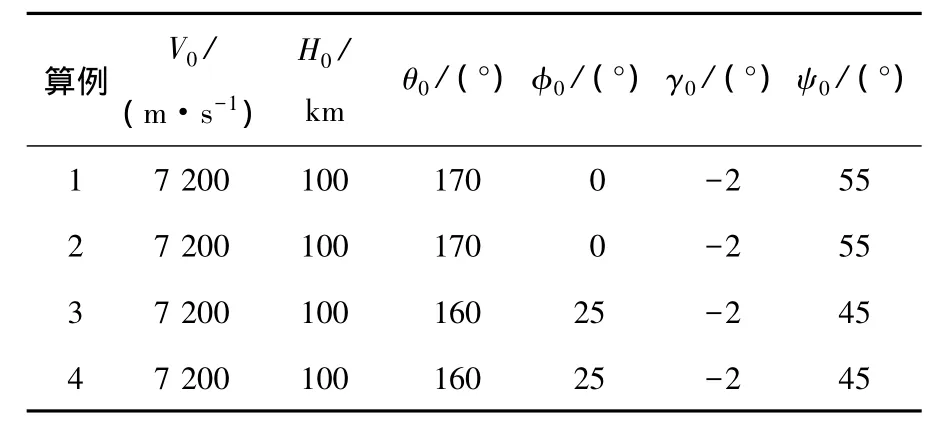
表1 标准条件再入初始参数

其中，算例1、2的再入初始条件一样.算例1不考虑禁飞圆约束，侧向制导采用传统航向角偏差走廊;算例2考虑禁飞圆C1约束，圆心经纬度为(240°，40°)，半径RC1=560 km(5°对应的大圆弧长)，用本文制导方法计算，与算例1形成对比.算例3、4的再入初始条件一样.算例3不考虑禁飞圆约束;算例4考虑禁飞圆C2约束，圆心位置与C1相同，半径RC1=780 km(7°对应的大圆弧长).

图3、4分别为三维再入轨迹曲线和地面航迹曲线，可见4个算例均到达目标点，满足航程约束，轨迹平滑.算例1、3的制导方法未考虑禁飞圆约束，轨迹穿过禁飞圆区域.算例2、4考虑禁飞圆约束，轨迹分别成功规避了禁飞圆C1、C2，表明了所提方法的有效性.

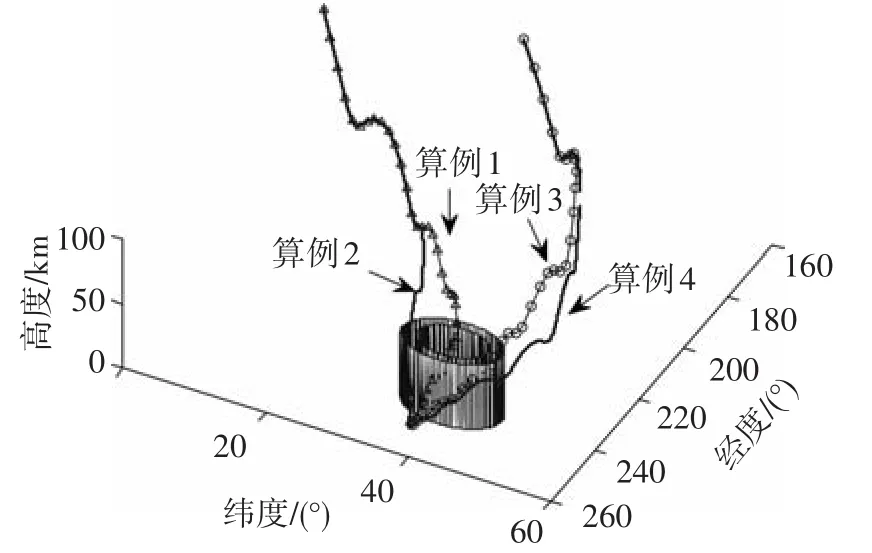
图3 三维再入轨迹

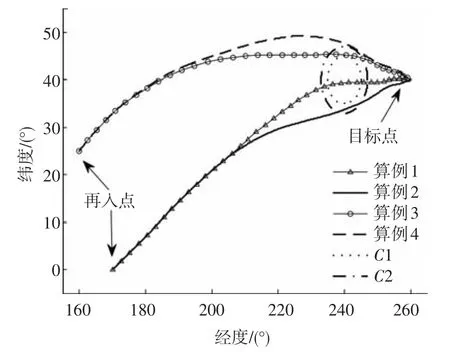
图4 地面航迹

图5、6分别为航向角偏差和倾侧角的历程曲线，表明了航向角偏差走廊对侧向运动的有效控制，因为走廊动态补偿为规避禁飞圆提供了更大的侧向机动范围，使得倾侧角翻转次数并未因规避禁飞圆而大量增加.当逐渐绕过禁飞圆时，航向角偏差也逐渐回归无禁飞圆的航向角偏差走廊，有效限制了轨迹的侧向误差.

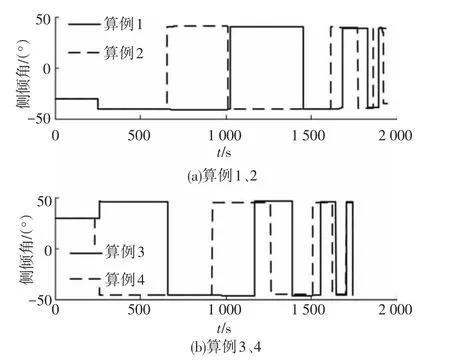
图5 控制变量σ时间历程

图7为热流密度、动压和过载的历程曲线，可见在4个算例中，过程约束均得到满足.

仿真过程中，制导指令生成时间大小主要取决于迭代校正引起的多次轨迹积分，最大制导周期指令生成时间＜500 ms，出现在初始下降段切换到拟平衡滑翔段后的第1次制导，之后很快变小，平均制导指令生成时间约为30 ms.

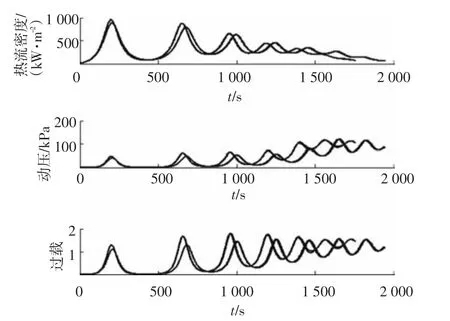
图7 过程约束时间历程

4.2 扰动条件下制导方法性能仿真

为验证制导方法的鲁棒性，对再入过程进行Monte Carlo轨迹仿真.每一步积分考虑的随机扰动包括:大气密度偏差(±25%)、飞行器质量偏差(±5%)、升力系数偏差(±10%)以及阻力系数偏差(±10%)，其中括号内数值表示偏差最大范围，制导系统对误差大小不可知.其他仿真设置与标准条件下仿真相同，算例2、4中各500次仿真结果的地面航迹见图8，制导精度统计见图9.可见，仿真飞行均绕过对应禁飞圆，满足航程要求，且轨迹平滑;终端位置偏差基本小于5 km，这对于再入制导而言精度是较高的.

本文制导方法将禁飞圆约束进行了转化，对于考虑禁飞圆约束的再入飞行，如果采用标准轨迹制导法，则落点精度低，对于不同的禁飞圆需要设计不同的标准轨迹，而且标准轨迹生成和优化算法较为复杂，如文献［7］所提方法.本文制导方法通过侧向制导即可满足禁飞圆约束，纵向制导采用数值预测校正方法，算法易于实现，制导精度高，且不依赖于标准轨迹，对不同的禁飞圆具有自适应性.

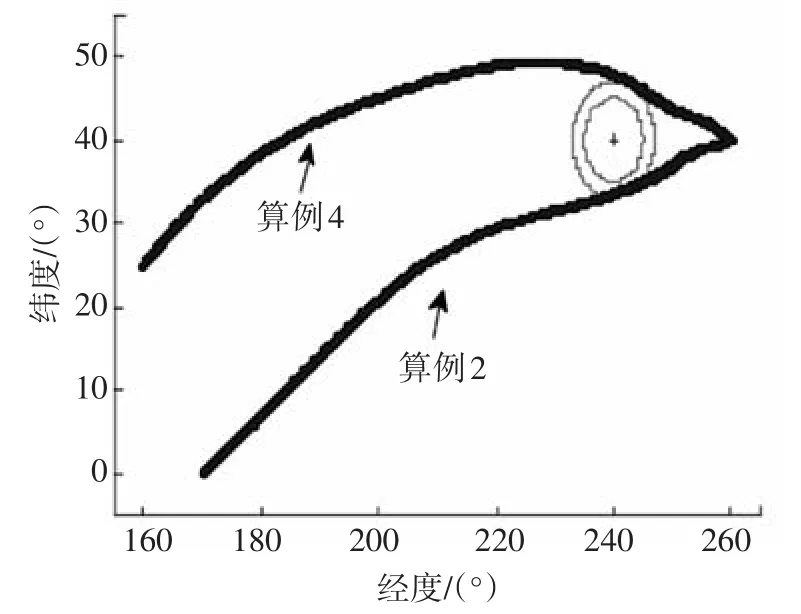
图8 扰动仿真地面航迹曲线

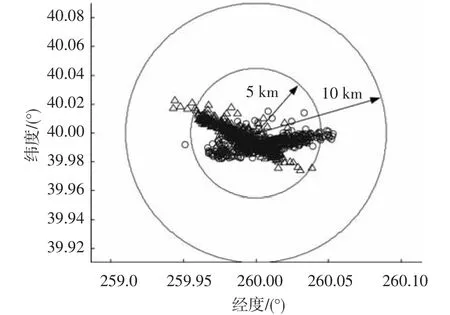
图9 扰动仿真终端点经纬度散布

5 结 论

1)提出了规避禁飞圆的预测校正制导方法，分别在纵向运动平面和侧向运动平面设计制导律以满足不同的约束.

2)纵向制导利用拟平衡滑翔条件，将过程约束转换成倾侧角约束，满足了过程约束，并使得轨迹较为平滑;侧向制导将禁飞圆的区域约束实时转化为飞行器航向角约束，同时应用偏差角走廊动态补偿策略，提供了足够大的侧向机动范围，使轨迹规避禁飞圆，并避免了倾侧角出现频繁翻转.

3)该制导方法不依赖于标准轨迹，偏差角走廊及制导变量均实时解算，在飞行能力允许情况下，不同的禁飞圆具有自适应能力.仿真落点数据也显示该方法具有很高的制导精度及鲁棒性.

［1］赵汉元.飞行器再入动力学和制导［M］.长沙:国防科技大学出版社，1997:7-22.

［2］ JOSHIA，SIVAN K.Predictor correctorreentry guidance algorithm with path constraints for atmospheric entry vehicles［J］.Journal of Guidance Control and Dynamics，2007，30(5):1307-1318.

［3］XUE Songbai，LU Ping.Constrained predictor-corrector entry guidance［J］.Journal of Guidance Control and Dynamics，2010，33:1273-1281.

［4］雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究［D］.长沙:国防科学技术大学，2008，81-82:109-112.

［5］王俊波，田源，任章.基于最优化问题的混合再入制导方法［J］.北京航空航天大学学报，2010，36(6):736-740.

［6］JORRIS T R，COBB R G.Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints［J］.JournalofGuidance Controland Dynamics，2009，32(2):551-572.

［7］谢愈，刘鲁华，汤国建，等.多约束条件下高超声速滑翔飞行器轨迹优化［J］.宇航学报，2011，32(12):2500-2504.

［8］雍恩米，钱炜祺，唐伟，等.考虑禁飞圆的滑翔式机动弹道与气动特性参数耦合设计［J］.航空学报，2013，34(1):66-75.

［9］VINH N X，BUSEMANN A，CULP R D.Hypersonic and planetary entry flight mechanics［M］.Ann Arbor，MI:Univ of Michigan Press，1980:26-27.

［10］SHEN Zuojun，LU Ping.Onboard generation of threedimensional constrained entry trajectories［J］.Journal of Guidance Control and Dynamics，2003，26:111-121.