3维Copula函数在降雨特征多变量频率分析中的应用

刘成林，周玉文，隋 军，高 琳

(1.北京工业大学建筑工程学院，100124北京;2.广州市市政工程设计研究院，510060广州;3.北京市水质科学与水环境恢复重点实验室，100124北京)

我国大部分城市的洪水主要由暴雨形成，与通过流量资料估算设计洪水相比，根据暴雨资料推求设计洪水是一种间接方法［1］，但在实际工作中经常遇到所在地点流量系列太短无法直接推求设计洪水的现象.降雨监测较为系统，数据序列长且完整，因此，通常基于降雨开展水文分析，进而确定城市洪涝系统设施规模.一般地，一场降雨通常可用雨量、历时和雨强等特征量以及雨量在时空上的变化来反映，设计降雨是地表径流计算的重要参数，主要包括以下特征要素:频率(重现期)、雨量(设计降雨量、次降雨量、降雨峰值)、历时(设计历时、总历时、峰值位置).目前，暴雨强度公式是普遍采用的设计降雨计算方法，是基于降雨量的单变量分析，不具备计算影响洪涝设施过流和调蓄能力的“降雨峰值”和“总降雨量”等特征量的功能.近几十年来，人们已经认识到采用单变量极值分布进行频率分析研究暴雨事件存在一定的局限性，开始探讨利用两变量联合分布描述暴雨不同特征值之间的相互关系，以更加全面地描述整个暴雨事件［2］，但用3变量及以上的联合分布描述暴雨事件的研究还鲜有报道.

Copula［3-4］是求解多变量概率问题优良的数学工具，该函数可将多个随机变量的边际分布连接起来得到其联合分布，是研究与变量尺度无关的相关性度量的一种途径，同时可以基于给定的边际分布构造联合分布.近几年，Copula函数理论广泛应用于降雨［2，5-7］、洪水［8-9］、干旱［10］和枯水［11］的多特征属性频率分析等问题.为此，以降雨特征量(设计降雨量、次降雨量和降雨峰值)频率研究为背景，引入3维Copula函数构建降雨特征变量的联合概率分布模型，研究不同量级降雨特征变量的遭遇概率及条件概率，以期为城市防洪排涝提供科学参考.

1 研究方法

1.1 Copula 函数简介

Copula函数是用来描述变量间相依关系的函数，不限定变量的边际分布.通过Copula模型可以将k个任意形式的边际分布连接起来，生成一个多变量联合概率分布模型.Copula函数的原理可参考文献［3-4，8］.Copula函数主要有3种类型，即椭圆型、阿基米德型和二次型.目前，在水文领域应用最广泛的是Archimedena Copula函数，其常见的3维Copula函数主要有 Clayton copula、Gumbel-Hougaard(GH)copula、Ali-Mikhail-Haq(AMH)copula和Frank copula(见表1).

表1 3维Copula函数

1.2 参数估计及拟合检验

Copula函数不限定变量的边际分布，确定适宜的边际分布是应用Copula函数的第一步.选用3种在水文频率分析中常用的分布线型(P-Ⅲ型分布曲线(P3)、对数正态分布曲线(LN2)和广义极值分布曲线(GEV))分别对“设计降雨量”、“降雨峰值”和“次降雨量”进行曲线拟合，采用概率点据相关系数检验法(PPCC)、拟优平方和准则法(RMSE)和拟优绝对值准则法(MAE)3种拟合优度检验方法确定出与各变量数据系列拟合效果最好的边际分布线型［12］.

Copula函数的参数估计主要有非参数法和参数法，其中非参数法要求有明确的Kendall'sτ与Copula参数θ的表达式，适用于单参数2维Copula函数的参数确定.而参数法相对比较灵活，本文采用参数法中的Inference of Functions for Margins(IFM)［13］方法确定 3维 Copula函数的参数.

IFM方法是将边际分布的参数与Copula函数的参数分别进行估计，该过程由以下步骤完成.

采用极大似然法(ML方法)［14］估计边际分布中的参数，即

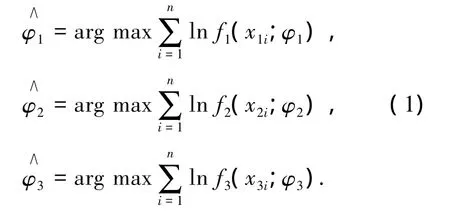
采用ML方法估计Copula中的参数

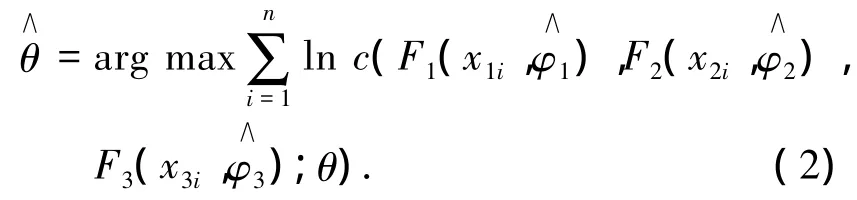
Copula函数在实际应用中的一个主要问题就是函数形式的选择.Embrechts等［15］对不同的Copula函数模型进行了比较，发现采用不同形式的Copula函数可能导致不同的分析结果，因此，选择合适的Copula函数尤为重要.检验与评价Copula函数的方法较多，本文采用AIC信息准则法(AIC)及离差平方和最小(OLS)准则法［9］对Copula函数的拟合优度进行评价.

1.3 风险概率

给定不同的变量条件可以得到不同的条件概率分布.主要考虑以下两种条件风险概率.

1)给定X3=x3，条件概率分布函数可表示为

式中fX3(x3)为x3的概率密度函数，其他符号意义同前.

2)给定X3≤x3，条件概率分布函数可表示为

2 研究区域概况

广州地处广东省东南部，珠江三角洲北缘，范围在东经 112°57'～114°3'，北纬 22°26'～23°56'，濒临南海，毗邻港澳.广州地处亚热带沿海，属海洋性亚热带季风气候，全年平均气温21.97℃，平均相对湿度68%，无霜期300～341 d，日照时数为1 571～2 053 h，市区年降雨量在1 700 mm以上.全年中，4～6月为雨季，7～9月天气炎热，多台风.

以广州市天河区五山站1961～2012年逐分钟自记数据为例，采用降雨强度法［16］将连续的降雨时间序列分割成降雨事件，按照“降雨强度小于0.1 mm/h，且持续时间超过10 h”的标准进行降雨数据分割，将1961～2012年的降雨时间序列分割为7 833场降雨事件，然后采用年最大值法进行取样.以设计历时720 min(即12 h)为例，取样样本52个，进而统计“设计降雨量”、“次降雨量”和“降雨峰值”3个表征雨型的特征变量，计算3者的联合概率分布和各条件下的遭遇概率分布.

3 结果分析

3.1 边际分布确定

图1为“设计降雨量”、“降雨峰值”和“次降雨量”边际分布的拟合结果.可以看出，所采用的3种分布线型与实测点据吻合较好，不同线型稍有差距，但总体上看均具有较好的拟合效果.

为了定量评价各分布线型的拟合效果，分别计算了各分布线型对于不同观测数据的RMSE、MAE及PPCC，结果见表2.对设计降雨而言，LN2分布具有最小的RMSE值，而GEV分布具有最小的MAE值和最大的 PPCC值.综合考虑，选定GEV分布作为数据的分布线型;对降雨峰值来说，GEV分布具有最小的MAE值，而LN2分布具有最小的RMSE值和最大的PPCC值，因此，选定LN2分布作为降雨峰值数据的分布线型;GEV分布对次降雨量具有最小的MAE、RMSE值和最大的PPCC值，所以，选定GEV分布作为次降雨数据的分布线型.

图1 设计降雨量、降雨峰值和次降雨量边际分布拟合

表2 边际分布拟合优度检验

3.2 Copula函数参数估计及拟合检验分析

采用阿基米德型Copula家族中应用较广泛的Frank Copula和AMH Copula函数分别构建降雨特征变量的联合分布.一般地，不同形式的Copula函数对于变量的相关性有不同的要求，Frank Copula函数对正、负相关关系的随机变量均适用;AMH Copula函数适用于弱相关关系的随机变量［13］.

为检验Copula函数的拟合精度，首先比较各个观测点对(xi，yi，zi)的经验累积概率和理论累积概率的一致性［9，13］.图 2 为经验频率与不同Copula函数理论频率的拟合图，可以看出，经验频率点和理论频率点均分布在45°线附近，总体上看，经验频率点和理论频率点拟合较好.Frank Copula函数的拟合精度(图 2(b))优于 AMH Copula函数(图2(a)).

图2 经验累积概率与理论累积概率比较

为了进一步确定“设计降雨量”、“降雨峰值”和“次降雨量”拟合最好的 Copula函数，利用MSE、AIC和OLS进行拟合优度评价.从表3可以看出，Frank Copula函数的3个评价指标值均小于AMH Copula函数，表明Frank Copula函数对3变量的拟合效果最佳.所以，选取Frank Copula函数作为“设计降雨量”、“降雨峰值”和“次降雨量”的联合分布函数.

表3 3维Copula函数拟合检验结果

3.3 风险概率分析

运用Frank Copula函数计算“设计降雨量”、“降雨峰值”和“次降雨量”的联合分布函数，根据1.3节公式计算条件风险概率.分别以100 a重现期的“设计降雨量”、“降雨峰值”和“次降雨量”为条件，计算其他两两变量组合的风险概率.从图3可以看出，与单变量等于某一设计值条件下的遭遇概率分布(图3(a)、(c)、(e))相比，对应条件下单变量小于等于某一设计值下的遭遇概率分布图(图3(b)、(d)、(f))显得“高”、“胖”，说明小于等于某一设计值条件下的风险概率出现的可能性更大.

以设计降雨条件为例，给出了几种重现期下降雨峰值和次降雨量遭遇的风险概率.表4为设计降雨量等于某一设计值(100，50，20和10 a)的条件下，降雨峰值和次降雨量同时小于等于某一重现期设计值的概率.可以看出，在设计降雨不变的情况下，降雨峰值和次降雨量遭遇的风险概率随着重现期的减小而降低，当降雨峰值和次降雨量设计值不变时，其遭遇的风险概率随着设计降雨重现期的减小而上升.具体来说，当设计降雨等于100一遇时，小于等于100 a一遇降雨峰值和次降雨量同时遭遇的概率为92.18%，而小于等于10 a一遇同时遭遇的概率仅为48.44%.表5为设计降雨小于等于某一设计值(100，50，20和10 a)的条件下，降雨峰值和次降雨量同时小于等于某一重现期设计值的概率.对比表4和表5可知，两种条件下的风险概率变化具有相似性，但设计降雨小于等于某一设计值条件下的风险概率出现的可能性更大.

从以上分析可以看出，设计降雨量、降雨峰值和次降雨量3变量之间具有较强的关联性，用多变量联合分布描述暴雨不同特征值之间的相互关系可以更全面地描述整个暴雨事件，细化水文分析前端输入，提高分析精度.具体地说，如进行50 a一遇水文分析时，根据表4，除给定设计降雨量值(218.9 mm)外，可根据城市等级及对安全度的需要，结合自身经济条件，同时选取某重现期的降雨峰值以及次降雨量作为输入，如50 a一遇的降雨峰值4.6 mm/min或 50 a一遇次降雨量271.6 mm来确定洪涝设施规模.

图3 降雨特征变量组合的条件风险概率

表4 设计降雨量等于某一设计值的条件风险概率

表5 设计降雨量小于等于某一设计值的条件风险概率

4 结论

1)基于3维Copula函数的降雨多变量分析方法，根据历史降雨数据，利用Copula联结函数，实现了3变量的联合分析，有效解决了单变量分析方法的不足，实现了对降雨事件特征真实全面的反映.

2)实际应用中，可基于设计降雨量确定设施标准，利用三者的组合风险概率复核次降雨量和降雨峰值的失效概率，为更科学合理地分析、评估和确定城市防洪排涝设施能力提供有效支撑.

3)如何基于地区特征、安全性和经济性的定量分析，优化降雨变量组合，科学合理地确定防洪排涝设施标准，是该方法需进一步研究的重点.

［1］ZHANG N，GUO S L，XIAO Y，et al.Design storm method based on bivariate joint distribution［J］.Water Power，2008，34(1):18-21.

［2］FONTANAZZA C M，FRENI G，LA LOGGIA G，et al.Uncertainty evaluation of design rainfall for urban flood risk analysis［J］.Water Science ＆ Technology，2011，63(11):2641-2650.

［3］SALVADORI G，DE MICHELE C.Frequency analysis via copulas:theoretical aspects and applications to hydrological events ［J］.Water Resources Research，2004，40(12):W12511.

［4］NELSEN R.An introduction to copulas［M］.New York:Springer Verlag，2006.

［5］ZHANG L，SINGH V P.Gumbel-Hougaard copula for trivariate rainfall frequency analysis［J］.Journal of Hydrologic Engineering，2007，12(4):409-419.

［6］武传号，黄国如，吴思远.基于Copula函数的广州市短历时暴雨与潮位组合风险分析［J］.水力发电学报，2014，33(2):33-41.

［7］ZHANG Q，LI J，SINGH V P，et al.Copula-based spatio-temporal patterns of precipitation extremes in China［J］.International Journal of Climatology，2013，33(5):1140-1152.

［8］ ZHANG L，SINGH V P.Bivariate flood frequency analysis using the copula method ［J］.Journal of Hydrologic Engineering，2006，11(2):150-164.

［9］侯芸芸，宋松柏，赵丽娜，等.基于Copula函数的3变量洪水频率研究［J］.西北农林科技大学学报:自然科学版，2010，38(2):219-228.

［10］SHIAU J T.Fitting drought duration and severity with two-dimensional copulas ［J］. Water Resources Management，2006，20(5):795-815.

［11］YU K X，XIONG L，GOTTSCHALK L.Derivation of low flow distribution functions using copulas ［J］.Journal of Hydrology，2014，508:273-288.

［12］李兴凯，陈元芳.暴雨频率分布线型优选方法的研究［J］.水文，2010，30(2):50-53.

［13］谢华，罗强，黄介生.基于三维copula函数的多水文区丰枯遭遇分析［J］.水科学进展，2012，23(2):186-193.

［14］MYUNG I J.Tutorial on maximum likelihood estimation［J］.Journal of Mathematical Psychology，2003，47:90-100.

［15］EMBRECHTS P，HÖING A，JURI A.Using copulae to bound the value-at-risk for functions of dependent risks［J］.Finance and Stochastics，2003，7(2):145-167.

［16］POWELL D N，AZIZ N M，KHAN A A.Impact of new rainfall patterns on the design of hydraulic structures［C］// Design of Hydraulic Structures. World Environmental and Water Resource Congress.Omaha:［s.n.］，2006:1-10.