预应力型钢超高强混凝土梁抗弯延性试验

贾金青，孟 刚，封 硕，朱伟庆

(海岸和近海工程国家重点实验室(大连理工大学)，116024辽宁大连)

随着社会经济的飞速发展，大跨重载桥梁和超高强建筑大量兴建，钢-混凝土组合结构不断涌现.中国研究人员在上世纪末提出了预应力型钢混凝土梁(PSRCB).PSRCB通过在内置实腹型钢混凝土梁中配置预应力筋，并施加预应力，保证组合梁高承载力的同时，改善了其正常使用阶段的工作性能，提高抗裂性能［1-3］.为了进一步提高受弯构件在大跨、重载、腐蚀环境下的服役寿命，在预应力型钢混凝土梁中应用超高强混凝土可进一步提高组合梁的承载力和刚度、减小梁截面尺寸，同时超高强混凝土密实度高、耐久性好，使得预应力型钢超高强混凝土梁(PSRUHSCB)在大跨重载桥梁、超高层建筑和深海海洋建筑中将具有广阔的工程应用前景.

超高强混凝土具有诸多优点的同时，其脆性破坏显著，超高强混凝土结构延性较差，制约了其在工程中的广泛应用［4］;预应力技术提高抗裂性的同时，对结构延性也产生不利影响［5］.因此，在现代结构形式中，注重结构承载力、耐久性的同时，需要注重结构的变形能力，以满足必要的延性性能，提高结构抵抗偶然超载、碰撞和反复荷载的能力.

目前，国内外学者分析了PSRCB的破坏形态、荷载-位移曲线模式和不同试验参数对其承载力的影响，并给出正截面抗弯极限承载力的计算公式，但未对PSRCB的延性性能进行分析［6-8］.而对于PSRUHSCB而言，相关文献报道较少，国内仅有 Meng等［9］通过 ANSYS有限元程序对PSRUHSCB抗弯承载力进行了数值分析.为探讨PSRUHSCB的抗弯延性性能，通过 15根PSRUHSCB和3根PUHSCB在静力荷载作用下的抗弯性能试验，分析了各试验因素对抗弯延性的影响规律，提出了考虑截面整体配筋情况的综合配筋指数ωc的计算方法，并通过数据曲线拟合，给出了以综合配筋指数ωc作为单一变量的PSRUHSCB位移延性系数的简化计算公式.

1 试验概况

1.1 试件设计

对15根PSRUHSCB和3根PUHSCB进行静力荷载作用下抗弯性能试验.梁长均为4 000 mm，跨度均为3 700 mm，截面尺寸为200 mm×300 mm，混凝土保护层厚度25 mm，普通纵向钢筋采用HRB335级钢筋，内置工字钢采用钢材牌号为Q235型钢，箍筋为HPB235级钢筋，预应力筋采用1860级高效低松弛钢绞线，预应力施加方式为后张法有粘结.箍筋的配筋满足构造配筋，保证试件梁的弯曲破坏，支座处500 mm范围内φ8@50，剪跨段范围内φ8@150，纯弯段范围内φ8@200.试验设计参数:有效预加力、钢绞线位置高度、型钢普通纵筋和预应力筋配筋率、含钢率、型钢位置.试件梁截面配筋形式见图1.试件设计参数见表1，表1中注释2部分说明了纯弯段变化型钢截面的不同方式，并依此研究不同含钢率对试件抗弯延性的影响;注释3中有效张拉应力值是通过粘贴在钢绞线表面的应变片实测而得.

1.2 材料力学性能

试件梁超高强混凝土标准立方体抗压强度平均值fcu=102.5 N/mm2，标准棱柱体抗压强度平均值fc=86.18 N/mm2，弹性模量Ec=4.87×104N/mm2，钢绞线、钢筋及型钢的屈服强度、极限强度及弹性模量实测值见表2.

表1 试件梁设计参数

图1 试验梁截面配筋示意(mm)

表2 钢绞线、钢筋和型钢实测力学性能 MPa

1.3 试验加载方案

试验采用四点弯曲分级加载方式，跨中纯弯段均为1 100 mm，剪跨段均为1 300 mm.荷载由1 000 t试验机在分配梁上施加，并通过荷载传感器测量施加荷载的大小，跨中梁底设置位移计测量试件的挠度，试验加载方式见图2.

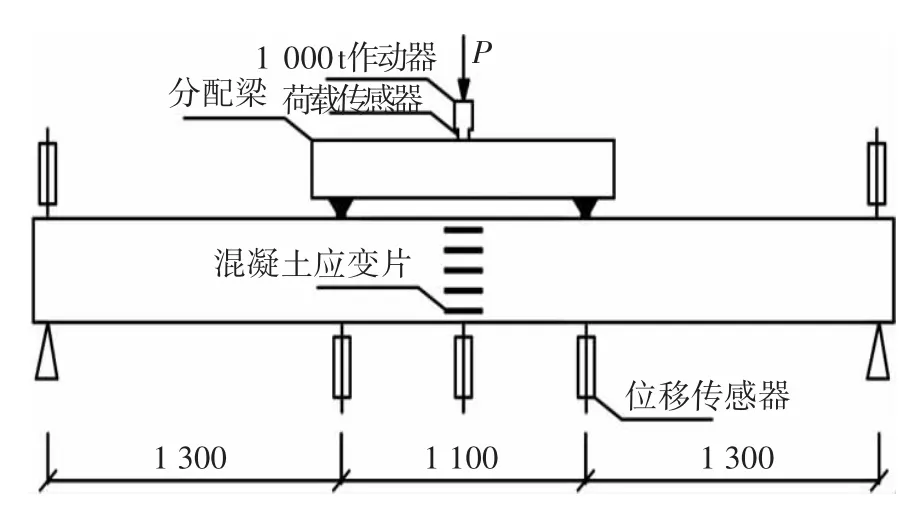
图2 试件加载图(mm)

1.4 试验结果

图3为15根PSRUHSCB荷载-位移曲线，图4为3根PUHSCB荷载-位移曲线.所有试件梁的开裂荷载Pcr、屈服荷载Py、极限荷载Pu见表3.由图3、4可见:1)PSRUHSCB的抗弯受力过程与普通型钢混凝土梁类似;试验梁开裂、屈服过程明显，当普通受拉纵筋屈服时，试验梁进入屈服状态;随着型钢腹板的逐步屈服和预应力钢绞线的应力继续增大，试验梁承载力继续上升;试验梁达到极限承载力状态时，由于保护层范围内的超高强混凝土脆性破坏，出现承载力骤降现象，但由于内置型钢存在，使得试验梁具有较好的持载能力;2)PUHSCB的抗弯受力过程与普通钢筋混凝土梁类似;普通受拉纵筋屈服时，试验梁进入屈服状态;由于预应力钢绞线的应力继续增大，试验梁的承载力进一步增加;达到极限承载力时，受压区超高强混凝土脆性破坏，截面刚度降低较大，试验梁丧失承载能力.

图5为部分试验梁在各级荷载作用下的跨中截面应变分布图.PUHSCB和PSRUHSCB在荷载达到0.9Pu之前，跨中控制截面沿梁高方向的应变基本呈较好的线性关系，两种型式的试验梁平截面假定基本符合;试验梁开裂后，随着荷载的增加，截面中和轴位置变化不大.

图3 PSRUHSCB荷载－位移曲线

表3 实测试验梁的开裂荷载、屈服荷载、极限荷载和位移延性系数

图4 PUHSCB荷载－位移曲线

图5 部分试件的跨中控制截面应变

2 延性性能分析

2.1 抗弯延性评价指标

延性是指材料、构件和结构体系在荷载作用或其他间接作用下进入非线性状态后，在承载力没有显著降低情况下的变形能力［10］.对于受弯构件的延性通常采用位移延性系数μΔ=Δu/Δy来描述［11］.

由于PSRUHSCB试件的荷载-位移曲线上屈服拐点不明显，采用文献［12］中的几何作图法来确定试件的屈服点，图6中屈服点对应的横坐标为屈服位移Δy，纵坐标为屈服荷载;对于极限位移Δu的取值，由于其荷载-位移曲线下降段上有较明显的持载现象，依据文献［13］Δu取截面抗弯承载力下降至极限承载力的80%时对应的跨中位移.

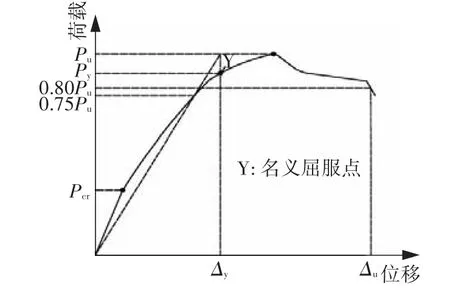
图6 PSRUHSCB荷载－位移曲线示意

对于PUHSCB，试验梁的荷载-位移曲线上屈服点明显，Δy取屈服荷载对应的跨中位移，试件的屈服荷载为普通受拉钢筋屈服时对应的所加荷载;Δu同样取截面抗弯承载力下降至极限承载力的80%时对应的跨中位移.试验梁实测的位移延性系数μΔ的试验结果见表3.

2.2 位移延性系数影响因数分析

钢绞线位置高度ap的影响:根据表3中试验梁 PUHSCB-01～03和 PSRUHSCB-06、15的试验结果，图7为钢绞线位置高度ap对PUHSCB和PSRUHSCB的位移延性系数的影响.PUHSCB和PSRUHSCB的位移延性系数随着预应力筋高度ap增大而线性增大，其原因为钢绞线布置越高，极限拉伸阶段越滞后，导致试验梁从屈服后到极限承载力状阶段，变形越大;当ap增大50 mm，PUHSCB的位移延性系数可增大 50.6%，PSRUHSCB的位移延性系数可增大15.4%.由此可见，钢绞线位置高度对PUHSCB和PSRUHSCB位移延性系数的影响较显著，并且内置型钢可改善预应力筋高度的降低对PSRUHSCB位移延性的影响.由于内置型钢限制了预应力筋布置，因此未设置ap=70 mm的PSRUHSCB试件.

有效预加力的影响:根据表3试验梁PSRUHSCB-01～03和PSRUHSCB-12～14的试验结果，钢绞线的有效预加力Pe=σpeAp.图8给出了两种截面形式下有效预加力对PSRUHSCB位移延性系数的影响.无论I、II型截面，PSRUHSCB位移延性系数随着有效预加力的增大而降低，且降低趋势基本呈线性关系;相同位移延性系数时，I型截面的PSRUHSCB试件可施加的有效预加力明显大于II型截面试件.

图7 预应力筋高度对位移延性系数的影响

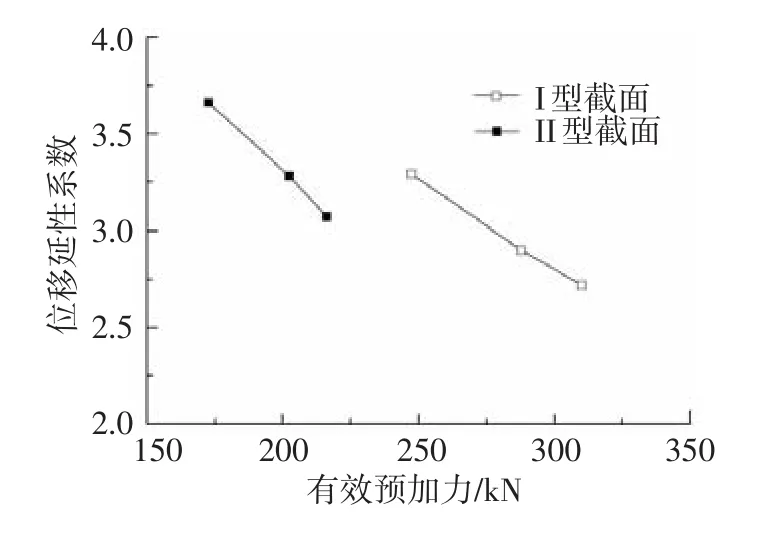
图8 有效预加力对位移延性系数的影响

普通纵筋配筋率和型钢位置的影响:定义普通纵筋配筋率ρs=As/bh0，根据表 3试验梁PSRUHSCB-02、04～05和07～09的试验结果，图9为I型截面的PSRUHSCB试件，在不同型钢位置时普通纵筋配筋率对位移延性系数的影响.型钢未偏移和型钢向下偏移时，ρs由0.58%增大到9.6%时，增大了 65.5%，PSRUHSCB 的位移延性系数均降低 22%，由 0.58%增大到 1.44%时，增大了148%，PSRUHSCB的位移延性系数均降低31%，且曲线规律相似;相同纵筋配筋时，型钢向下偏移30 mm后，位移延性系数均降低18%左右.另外由II型截面的试件PSRUHSCB-15、17试验结果，ρs由 0.58%增大到 1.44%，位移延性系数降低29.2%.由此可见，PSRUHSCB位移延性系数随着普通纵筋配筋率的提高而降低的趋势与普通钢筋混凝土梁一致，且内置型钢的位置变化基本不会影响上述规律.

型钢含钢率的影响:试验中通过对I14工字钢增大下翼缘和腹板的面积，产生不同的含钢率，定义含钢率ρa=Aa/bh0.根据表 3中试件PSRUHSCB-02、10～11的试验结果，图10为型钢含钢率对PSRUHSCB位移延性系数的影响.含钢率的增大导致了PSRUHSCB位移延性系数降低，因为含钢率的增大等同于增大了普通纵筋配筋率，导致位移延性系数降低.ρa提高 20.4%，PSRUHSCB的位移延性系数降低了7.2%.试验中未考虑通过增大型钢上翼缘来变化含钢率对试件位移延性系数的影响.

图9 普通纵筋配筋率对位移延性系数的影响

图10 型钢含钢率对位移延性系数的影响

预应力筋配筋率的影响:由表3中试件PSRUHSCB-05～06试验结果，定义预应力筋配筋率ρp=Ap/bh0，ρp增大40.5%时，PSRUHSCB 位移延性系数降低了22%.由此可见，相对于普通纵筋配筋率，预应力筋配筋率对PSRUHSCB位移延性系数的影响更为显著.

由表3中试件PSRUHSCB-06和PUHSCB-03、PSRUHSCB-09和PUHSCB-02的试验结果得出，相同预应力筋和普通纵筋配筋时，相对于PUHSCB，PSRUHSCB的位移延性系数并未得到明显提高，甚至会降低.其原因为:内置型钢的作用，主要是改变了梁的荷载-位移曲线模式，使其具有一定持载能力;然而内置型钢也相当于增大了截面的配筋，同时提高了抗弯刚度，限制了挠度的增加，进而降低了延性系数.

3 综合配筋指数与延性的关系

对于PSRUHSCB，梁截面内受拉区提供抗力的单元较多，强度和配置位置各不相同，上述分析的各试验因素对PSRUHSCB位移延性系数均有较显著影响.对于传统的预应力混凝土梁，可采用配筋指数ω=(Apfpy+Asfy)/fcbh0来反应梁截面的配筋情况［14］，进而分析梁的承载力和位移延性系数的变化规律，但采用配筋指数来反映PSRUHSCB的截面配筋情况，无法完整体现钢绞线和型钢的配置对PSRUHSCB受力性能的影响.因此，为了简化部分预应力型钢超高强混凝土梁弯曲延性分析，需要寻找一个统一的指标，考虑梁截面内型钢和钢绞线的配置情况，将不同屈服强度的钢材等效为普通受拉纵筋，并将预应力筋和型钢面积按照配置高度进行折减，引入综合配筋指数ωc，其计算公式为

式中:As、Ap、Aaf、Aaw分别为普通受拉纵筋、钢绞线、型钢下翼缘和型钢全腹板面积，由于型钢截面中主要由下翼缘和腹板提供梁截面的拉应力，综合配筋指数ωc中不考虑型钢上翼缘;fy、fa、fc分别为普通受拉纵筋、型钢受拉屈服强度实测平均值和混凝土棱柱体抗压强度实测平均值.由于钢绞线没有明显的屈服点，fp为钢绞线受拉强度，其计算公式为

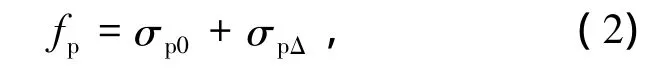
式中:σp0为预应力筋合力点处混凝土法向应力等于零时的预应力筋应力，计算方法见规范

［15］;σpΔ为预应力合力点处混凝土法向应力等于零时至试验梁承载力极限状态时的预应力筋应力增量，可由平截面假定计算得出.

式(1)中kp、kaf、kaw分别为钢绞线、型钢下翼缘和型钢腹板面积的折减系数.由图5和图7的分析可以看出:型钢上翼缘处应力基本为零或者应力较小，因此式(1)中未考虑型钢上翼缘的贡献;钢绞线和型钢的配置位置对延性性能影响较大，且钢绞线位置高度与PUHSCB的位移延性系数基本呈线性关系.将钢绞线和型钢假设为普通受拉纵筋，以普通受拉纵筋的配置位置为基准，将钢绞线和型钢按照基准位置进行截面面积折减，折减系数计算公式为:

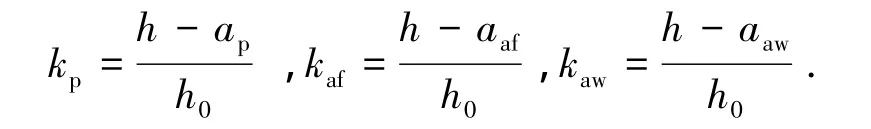
式中:h、h0、ap、aaf、aaw分别为梁截面高度、普通受拉纵筋中心距梁受压边缘的距离、钢绞线中心距梁受拉边缘的距离、型钢下翼缘中心距梁受拉边缘的距离和型钢腹板中心距梁受拉边缘的距离.对PUHSCB计算综合配筋指数时，式(1)不考虑型钢的贡献.PSRUHSCB和PUHSCB的综合配筋指数计算结果见表4.

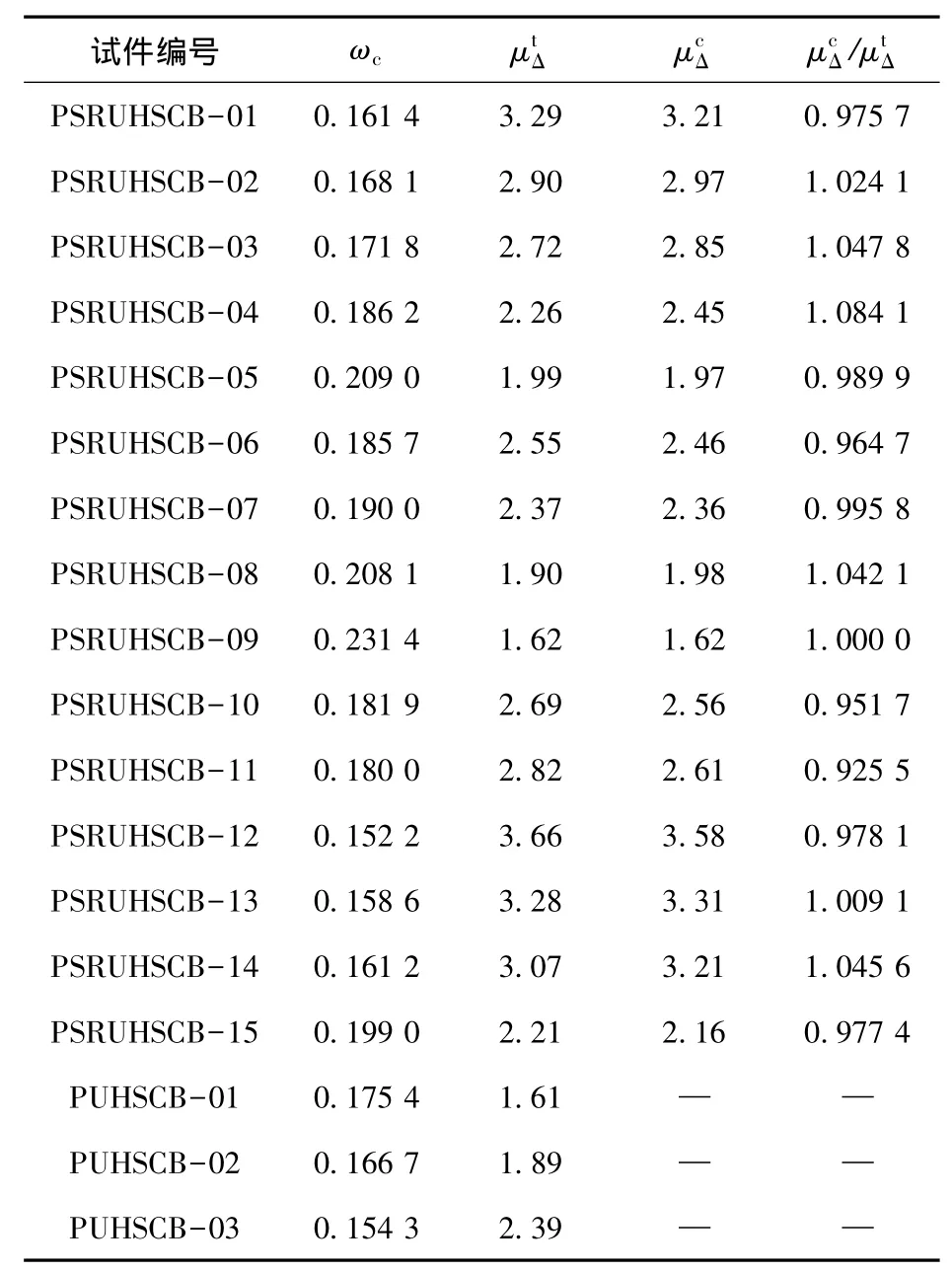
表4 位移延性系数计算结果对比

图11给出了综合配筋指数与位移延性系数的关系.PUHSCB的位移延性系数μΔ随着综合配筋指数ωc的增大而减小;PSRUHSCB的位移延性系数μΔ与综合配筋指数ωc关系趋势明显，随着ωc的增大，μΔ呈非线性降低，且降低速率越来越缓慢，其规律与普通受拉纵筋配筋率对钢筋混凝土梁位移延性系数的影响规律基本一致;当综合配筋指数相同时，PSRUHSCB的位移延性系数明显大于PUHSCB.因为，内置型钢调整了截面总体配置钢材的位置，使得预应力型钢超高强混凝土梁具备一定的峰值后持载能力，其位移延性系数明显大于预应力超高强混凝土梁.通过数理统计方法给出了PSRUHSCB位移延性系数关于综合配筋指数单一变量的曲线拟合公式:

当预应力型钢超高强(强度等级C100)混凝土梁发生类似钢筋混凝土适筋梁的破坏形态，同时梁内型钢不发生向上偏移时，式(3)在0.15≤ωc≤0.24范围内适用.由于PUHSCB的试件较少，未进行数据拟合.按照式(3)计算的PSRUHSCB位移延性系数计算值与试验值对比结果见表4.计算值μcΔ与试验值μtΔ之比的平均值为1.000 8，标准差为0.040 6，计算结果与试验结果吻合较好.

图11 综合配筋指数对位移延性系数的影响

4 结 论

1)内置型钢改变了预应力超高强混凝土梁的荷载-位移曲线模式，使得预应力型钢超高强混凝土具有一定的峰值荷载后持载能力.

2)预应力型钢超高强混凝土梁的位移延性系数μΔ与综合配筋指数ωc关系趋势明显，随着ωc的增大，μΔ呈非线性降低，且降低速率越来越缓慢;并通过数理统计的方法给出了位移延性系数μΔ关于综合配筋指数ωc的曲线拟合公式，公式计算值和试验值吻合较好.

3)相同综合配筋指数ωc时，由于内置型钢调整了截面总体配置钢材的位置，使得预应力型钢超高强混凝土梁具备一定的峰值后持载能力，其位移延性系数明显大于预应力超高强混凝土梁.

［1］ ZHANG Boyi，ZHENG Wenzhong.Experimental research on mechanical properties of prestressed truss concrete composite beam encased with circular steel tube［J］.Journal of Harbin Institute of Technology(New Series)，2009，16(3):338-345.

［2］李峰.预应力钢骨混凝土梁承载能力试验研究［D］.重庆:重庆大学，2007:1-2.

［3］薛伟辰，杨枫，苏旭霖，等.预应力钢骨混凝土梁低周反复荷载试验研究［J］.哈尔滨工业大学学报，2007，39(8):1185-1190.

［4］蒲心诚.超高强高性能混凝土［M］.重庆:重庆大学出版社，2004:1-6.

［5］张利梅.高效预应力混凝土梁受力性能及延性研究［D］.大连:大连理工大学，2004:86-85.

［6］傅传国，李玉莹，梁书亭.预应力型钢混凝土简支梁受弯性能试验研究［J］.建筑结构学报，2007，28(3):63-73.

［7］郑文忠，王钧，韩宝权.内置H型钢预应力混凝土连续组合梁受力性能试验研究［J］.建筑结构学报，2010，31(7):23-31.

［8］熊学玉，高峰.预应力型钢混凝土框架试验研究及分析［J］.四川大学学报:工程科学版，2011，43(6):1-8.

［9］MENG Gang，ZHANG Lihua，JIA Jinqing.Numerical analysis on flexuralcapacity ofprestressed steel reinforced ultra-high strength concrete beams［J］.Key Engineering Materials，2013，531/532:429-434.

［10］范立础，卓卫东.桥梁延性抗震设计［M］.北京:人民交通出版社，2001:320-324.

［11］张利梅，赵顺波，黄承逵.预应力高强混凝土梁延性性能分析与试验研究［J］.工程力学，2005，23(3):166-171.

［12］PARK R.Evaluation of ductility of structures and structural sub-assemblages from laboratory testing ［J］.Bull New Zealand Soc Earthquake Engineering，1989，22(3):155-166.

［13］Frédéric Légeron，Patrick Panltre.Behavior of highstrength concrete columns under cyclic flexure and constant axial load［J］.ACI Structural Journal，2000，97(4):591-601.

［14］罗小勇，陈跃科，邓鹏麒.无粘结部分预应力混凝土梁的疲劳性能试验研究［J］.建筑结构学报，2007，28(3):98-104.

［15］GB50010—2010混凝土结构设计规范［S］.北京:中国建筑工业出版社，2010.