LNG储罐穹顶带钢板网壳施工全过程稳定性分析

翟希梅，王 恒

(1.哈尔滨工业大学 土木工程学院，150090哈尔滨;2.中国建筑西南设计研究院有限公司，610041成都)

液化天然气(liquefied natural gas，LNG)储罐穹顶是由钢筋混凝土壳、内衬钢板及单层肋环型钢网壳组成.在穹顶混凝土施工过程中，内衬钢板与单层钢网壳对浇筑过程中的壳体混凝土及施工荷载起到模板及支承作用，必须满足一定的承载力及刚度要求.现有研究工作对带蒙皮(钢板)网壳结构的全过程非线性稳定性分析并不深入，相关文献仅对铺钢板肋环型网壳的煤气柜柜顶结构进行了特征值屈曲分析和稳定性分析［1-2］，采用MIDAS或SAP2000对LNG储罐穹顶带钢板网壳进行了工程性质的受力性能分析［3-6］.

本文针对160 000 m3LNG储罐穹顶的带钢板网壳结构，以ANSYS软件为数值模拟平台，建立精细化有限元模型，并提出合理的施工阶段稳定性分析方案，对该结构进行了非线性全过程稳定性研究;探讨了网格尺寸、蒙皮钢板厚度、网壳杆件截面尺寸、矢跨比、初始几何缺陷形式及大小对带钢板网壳稳定性能的影响规律.

1 穹顶网壳结构简介及模型建立

160 000 m3LNG储罐穹顶的单层网壳结构一般采用肋环型球面网壳，球面半径82 m，矢高11 m，跨度 82 m(矢跨比为 1/7.5)，见图 1.肋梁数由外到内分别为96、48、24和8根;内圈(1～4圈)环梁截面及第1、2圈环梁间的肋梁截面为H350×250×8×12，外圈环梁(5～9 圈)截面及其余肋梁截面为 H350×174×6×10.钢板厚 6 mm，钢材材料为Q345E.

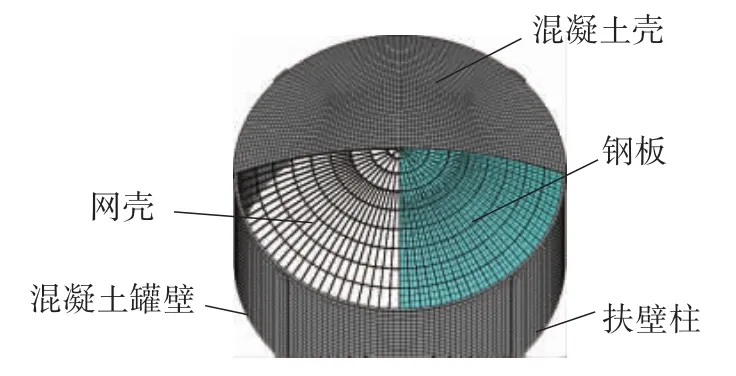
图1 LNG储罐模型

穹顶网壳结构有限元模型见图2.模型中，采用BEAM188单元模拟网壳结构的梁构件，用SHELL181单元模拟钢板.建模时将梁单元节点偏移至梁截面翼缘顶面、壳单元节点偏移至壳单元底面，从而使梁、壳单元共节点，以模拟梁板固结.网壳结构支座处的边缘梁、壳单元节点采用固接约束.钢材材料特性参数取值为:弹性模量2×105MPa，泊松比 0.3，密度 7 850 kg/m3;采用多线性等向强化模型MISO，材料本构关系为理想弹塑性，屈服强度345 MPa.

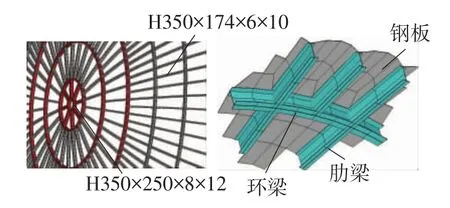
图2 有限元模型

2 单层肋环型网壳稳定性分析

在分析带钢板网壳的受力性能前，先对单层肋环型网壳进行稳定性分析，以期与后面带钢板网壳的稳定性进行对比.荷载采用的是满跨均布荷载，网壳有限元模型中的梁单元尺寸约为0.5 m.图3是肋环网壳的非线性分析结果，其中图3(a)是网壳失稳后产生最大转角位移节点的荷载-转角位移曲线及网壳失稳后产生最大竖向位移节点的荷载-竖向位移曲线.通过两曲线对比，以及通过网壳杆件的转角位移云图(图3(b))可以判断，网壳失稳是局部环梁的扭转失稳，其发生位置位于第5、6、7圈的环梁处，而失稳时第六圈部分环梁(与8根最长的肋梁相连接的环梁)已经产生塑性应变，进入塑性阶段.网壳的稳定承载力为2.71 kN/m2.

由于网壳的失稳模式是局部环梁的扭转失稳，不能从荷载-位移全过程分析中获得初始缺陷形式，因此采用特征值屈曲分析，将最低阶整体屈曲模态形式作为肋环网壳的初始缺陷形式，并取缺陷最大值分别为跨度的 1/1 000、1/500、1/300，相应的网壳极限屈曲承载力为 2.24、1.90、1.61 kN/m2(见图 3(c)实线曲线).

图3 肋环网壳非线性分析结果

网壳失稳是由部分环梁屈服致使局部刚度急剧弱化而引起的，文献［7］将这种失稳模式定义为提前失稳，这类失稳属于杆件配置不合理导致的.因此将上述发生杆件扭转屈曲的第5、6、7圈环梁截面从原先的H350×174×6×10(截面 I)增大至 H350×250×8×12(截面 II)，再重新进行稳定性分析.

增大截面后，失稳模式改变为局部区域凹陷，见图4.失稳时网壳处于弹性阶段，属于弹性失稳.图3(c)荷载-位移曲线对比显示，稳定承载力提升为 3.01 kN/m2，较更改前提高了 11.1%.改变截面后网壳在不同大小初始缺陷下，表现为弹塑性失稳，而稳定承载力较更改前分别提高了3.1% ～3.7%;而增强截面，所需用钢量增加5.5%.考虑到初始缺陷的影响，本文5～7环局部杆件的截面增强对稳定承载力的提高作用不明显.

图4 改变梁截面后网壳在失稳后的竖向位移云图

3 带钢板网壳的稳定性分析

3.1 单元尺寸的确定

有限元模拟中，梁、壳单元的组合一直是难点问题，其中合适的单元网格尺寸是决定计算收敛、结果精度及机时耗费的重要因素.在以位移参数作为基本未知量的有限元单元法(位移元)中，位移的精度高于应力［8］，也即单元之间变形是协调的，但不能保证其应力场连续，通常在单元节点处进行平均化处理.因此，本文采用文献［9-10］提出的能量误差e来判断网格划分的精度，并通过比较不同单元划分尺寸下的计算结果，以获得合理的有限元模型单元尺寸.能量误差e的表达式为:

式中:ei为单元能量误差，U为模型中所有单元的应变能总和，Vi为单元体积，Δσ为单元节点应力和节点平均应力的差值，［D］为弹性系数矩阵.

重力荷载作用下，按不同单元划分的有限元模型的能量误差见表1.单元划分方式1～4的能量误差较低，其计算结果精度较好;而单元划分方式5、6的能量误差较高，获得的计算结果的精度不足.图5是分别按表1的6种单元划分方式获得的网壳屈曲处杆件节点的荷载-竖向位移曲线，发现网格划分方式对网壳的稳定承载力计算结果影响很大.单元划分方式1和方式4下的荷载位移曲线接近(以方式1下的极限承载力为准，方式2、3、4下的极限承载力分别与其相差6.6%、9.1%、0.6%)，考虑到单元尺寸越小，有限元计算过程中刚度矩阵越容易变奇异导致计算不收敛，计算不出结构的极限承载力，因此，本文采用单元划分方式1.

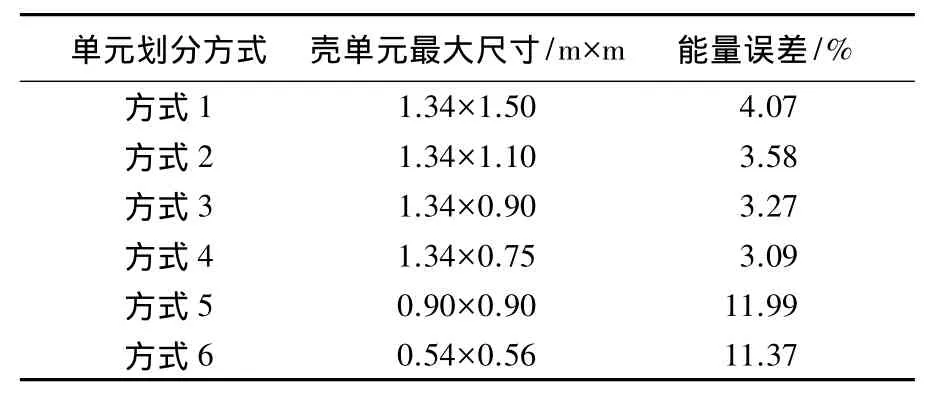
表1 不同单元划分方式下模型的能量误差

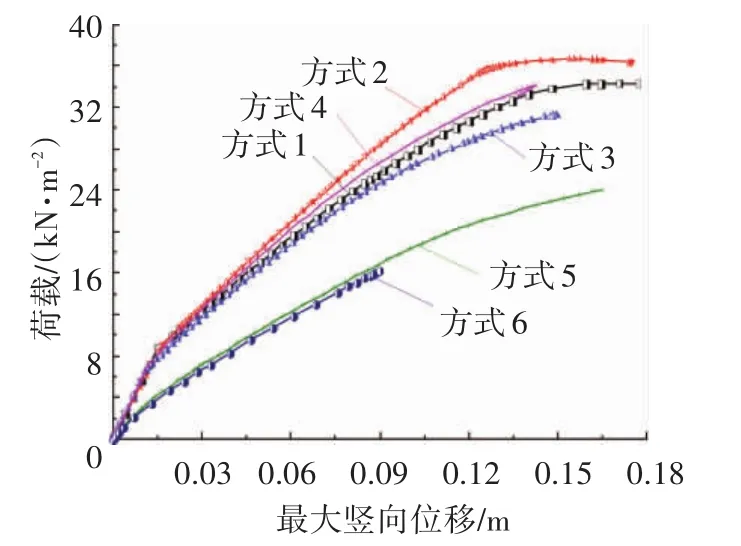
图5 不同单元划分对计算结果的影响

3.2 带钢板网壳稳定性分析

本节带钢板网壳的稳定性计算中，施加的荷载仍为均布面荷载，并根据计算适用性分别选择弧长法或Newton-Raphson方法，当采用Newton-Raphson方法时选择稀疏矩阵求解器.

3.2.1 初始缺陷的确定

在荷载-位移全过程稳定分析中，将结构屈曲前、后两个邻近状态的位移之差作为该临界点屈曲模态的精确形式，而初始缺陷的形式与此屈曲模态形式一致，文献［11］将此种确定初始缺陷形式的方法称为“一致缺陷模态法”，这就需要计算出网壳的分枝平衡路径.文献［12-13］采用位移扰动法和力扰动法实现了对单层网壳分枝平衡路径的跟踪，文献［11］也提出“扰动荷载法”计算网壳进入分枝后的平衡路径，文献［11］同时指出在增量计算中计算的累积误差就可以看作是一种扰动，当累积误差达到一定程度，计算将自动进入分枝后的平衡路径，计算累积误差随着自由度数的增加及计算步数的增加而增加.

图6是1/8矢跨比时网壳的非线性分析结果(其他矢跨比下网壳的计算结果规律类似).本文计算过程中，如当所用的荷载子步数较少时，计算将沿着平衡路径I进行，产生图6(a)的失稳模式I(网壳顶部凹陷);当荷载子步数多时，计算将沿着平衡路径II进行，产生图6(b)的失稳模式II(网壳外圈环梁处凹陷).图6(c)是带钢板网壳上A处钢板上某节点在两种平衡路径下的荷载位移曲线，图6(c)中圆圈标记的地方即为网壳两种平衡路径的分枝点.

分别取平衡路径I上临界点处的屈曲形式(图6(a))和平衡路径II上临界点处的屈曲形式(图6(b))作为带钢板网壳结构的初始几何缺陷形式，称为初始缺陷I和初始缺陷II，初始缺陷的最大计算值取跨度的 1/300［14］，结构的荷载-最大位移曲线见图6(d).对比结果显示:网壳的失稳模式与各自施加的初始缺陷形式一致;初始缺陷Ⅱ下比初始缺陷Ⅰ下的网壳失稳荷载低，即进入平衡路径Ⅱ后的失稳模式(即失稳模式II)是网壳的最不利失稳模式.在本文网壳结构的非线性分析中，采用文献［11］给出的建议，保证荷载子步数都足够大，以计算出平衡路径II，并将结构进入平衡路径II后的屈曲模式作为初始几何缺陷形式.

图6 带钢板网壳(矢跨比1/8)的分析结果

JGJ 7—2010《空间网格结构技术规程》［14］规定，球面网壳的全过程分析，初始几何缺陷的最大计算值可按网壳跨度的1/300取值，而实际工程LNG穹顶带钢板网壳安装允许偏差更为严格;因此，本文设定了3个初始缺陷的最大计算值，分别为跨度的 1/1 000、1/500、1/300.

3.2.2 非线性稳定分析结果

图7是6 mm钢板网壳，矢跨比为1/7.5的非线性分析结果.如图7(a)、(b)所示，带钢板网壳的失稳模式是第5～8圈环梁处局部凹陷，失稳时梁、板局部进入塑性，属于弹塑性失稳［7］.图7(c)是带钢板网壳上产生最大节点竖向位移处的荷载-位移曲线.不考虑初始缺陷时，网壳极限承载力为34.41 kN/m2，与图3纯网壳比较，带钢板网壳较纯网壳的极限承载力提高11.70倍;当初始缺陷取值比例分别为 1/1 000、1/500、1/300时，带钢板网壳较纯网壳的极限承载力分别提高9.87、8.78、7.76 倍，可见蒙皮对网壳承载力的提高是非常显著的;随初始缺陷的增大，网壳承载力降低，初始缺陷比例为1/300时，网壳极限承载力为14.10 kN/m2，较无缺陷时下降了 59.0%，此时，带钢板网壳只有梁构件局部进入塑性，蒙皮钢板处于弹性阶段.

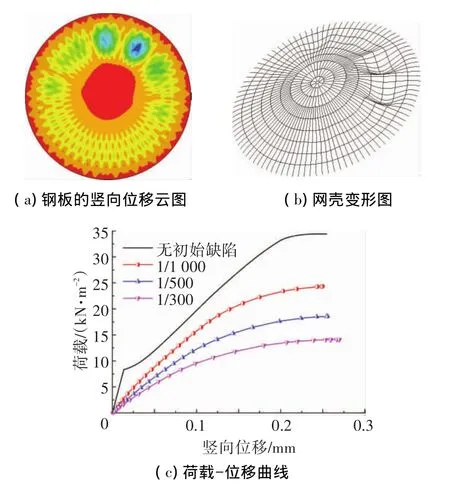
图7 带钢板网壳(矢跨比1/7.5)的分析结果

在穹顶混凝土浇筑过程中，考虑将浇筑施工过程中的混凝土自重视作均布外荷载，600～800 mm厚的混凝土相当于15～20 kN/m2的均布面荷载(混凝土容重取25 kN/m3)，由此看出，若只考虑无钢板的肋环型网壳承力(无初始缺陷时的稳定承载力为2.71 kN/m2)，远远不能满足施工设计要求，所以必须考虑蒙皮对网壳的加强作用.本文的计算结果还表明，当初始缺陷较大时(1/300)，蒙皮网壳结构稳定承载力(14.10 kN/m2)是不足以承载600 mm混凝土自重的(15 kN/m2).

4 带钢板网壳的优化设计参数分析

4.1 钢板厚度

不考虑初始缺陷，分别按 1、2、3、4、5、6、7 mm钢板厚度条件进行网壳的稳定性分析，结果见图8及表2.当钢板厚度在2～7 mm范围内，随着板厚的增加，极限稳定承载力的增长幅度基本稳定;不同板厚下带钢板网壳的失稳方式皆为局部凹陷型失稳模式;随着板厚的增加，失稳时凹陷的位置向外圈处移动，例如:2 mm板厚时，结构失稳的位置在第4、6圈环梁之间(见图8(b))，6 mm板厚时结构失稳的位置在第7、8圈环梁之间(见图8(c)).

图8 钢板厚度对极限承载力的影响

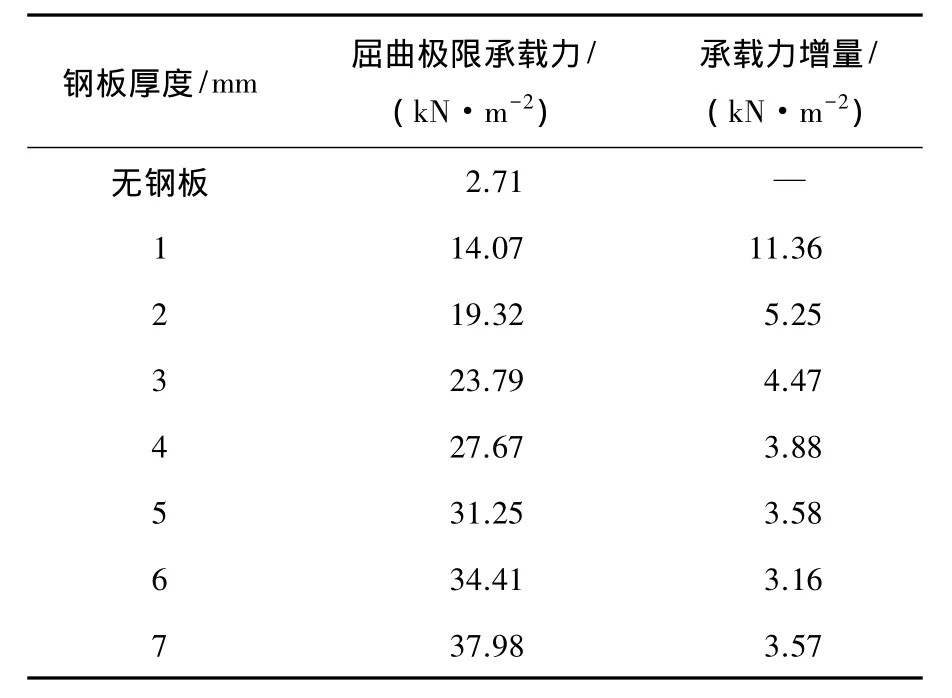
表2 不同板厚条件下屈曲极限承载力对比

4.2 网壳杆件截面

第2节的分析结果显示，结构5、6、7环的网壳杆件是结构的薄弱环节，为此本文考虑将此环梁截面从原先的 H350×174×6×10(截面Ⅰ)提高为 H350×250×8×12(截面Ⅱ)，与第 2节中纯网壳稳定性计算的截面更改一致，钢板厚度采用6 mm，矢跨比 1/7.5，结果见图 9.图 9(a)显示:更改截面后，网壳最大承载力由34.41 kN/m2提升到36.89 kN/m2(无初始缺陷)，较更改前提高了7.2%，当分别考虑 1/1 000、1/500、1/300 比例初始缺陷时，截面更改致使网壳稳定承载力提高13.8%、18.2%、22.1%.另外，从图 9(b)可看出，截面更改后，失稳模式没有改变，但失稳位置更加靠近外圈环梁(与图7(b)比较).与本文第2节内容比较，同样的梁截面调整，考虑初始几何缺陷时，纯网壳结构的稳定承载力提高3.1%～3.7%，而带钢板网壳的稳定承载力提高13.8%～22.1%.

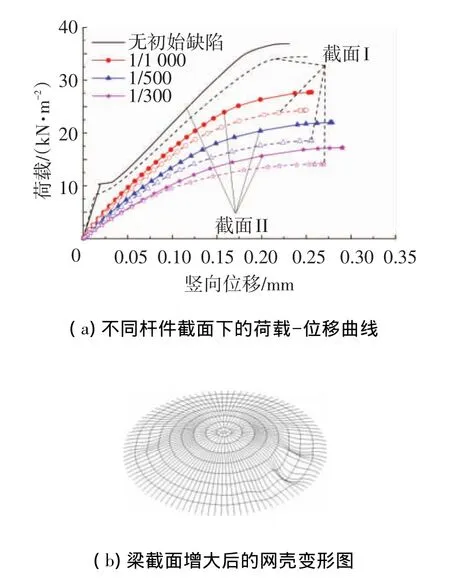
图9 截面尺寸对网壳承载力的影响

4.3 网壳矢跨比及初始缺陷

上述分析中，网壳的矢跨比为11/82=1/7.5，本节进行矢跨比对带钢板网壳稳定性影响探讨时，另增设4个矢跨比，分别为1/8、1/7、1/6和1/5.

表3和图10是不同矢跨比网壳在不同比例初始缺陷下的极限承载力比较.结果表明，1/8～1/5矢跨比范围内，随矢跨比的增加，结构稳定极限承载力逐渐提高，不同程度的初始缺陷下，最大增幅为78.7%～87.3%;初始缺陷是影响极限承载力的重要因素，同一矢跨比下，1/1 000、1/500、1/300比例初始缺陷时，结构的极限承载力较无初始缺陷下的结构承载力分别降低26.8%～60.6%;另外，在1/8～1/5取值范围内时，当矢跨比为1/7，带钢板网壳对初始缺陷的敏感程度最高.由此可见，如果工艺上允许，提高网壳的制作精度、适当增大矢跨比将对网壳的极限承载力提高很多.

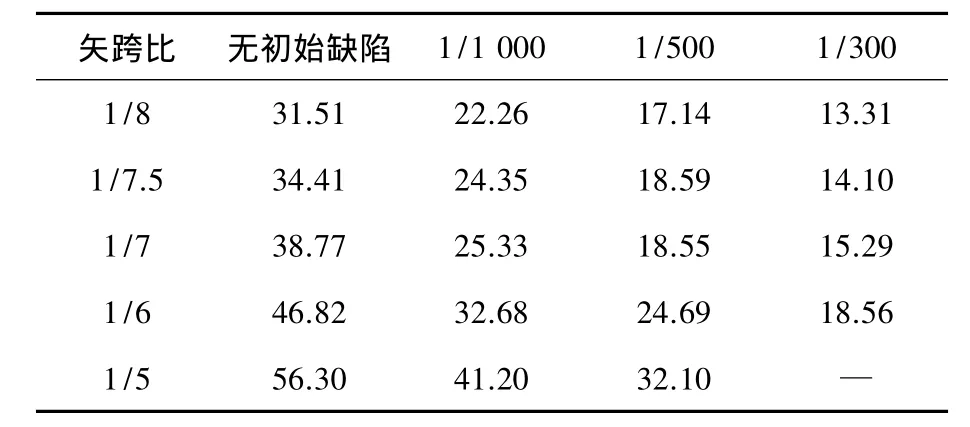
表3 不同矢跨比下结构的极限承载力 kN·m-2

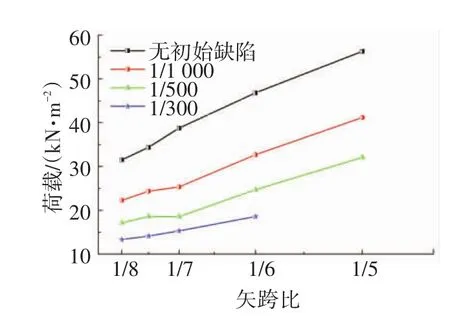
图10 不同矢跨比网壳的稳定极限承载力

5 结论

1)蒙皮钢板的存在将改变原有肋环型网壳的失稳模式，且对网壳极限稳定承载力的提高异常显著，初始缺陷越小，提高程度越大.

2)在2～7 mm钢板厚度选取范围内，网壳的失稳模式皆为局部凹陷型失稳，随着板厚的增大，极限稳定承载力增幅基本稳定，且网壳失稳时凹陷的位置逐渐向外圈移动.

3)局部增大网壳杆件截面，可以有效提升带钢板网壳的稳定极限承载力，本文中局部杆件的截面增强对纯网壳稳定承载力的提高作用不明显，但在不同初始缺陷取值下，带钢板网壳的承载力可以提升 7.2%～22.1%.

4)1/8～1/5矢跨比范围内，随矢跨比的增加，带钢板肋环型网壳结构稳定极限承载力逐渐提高，不同程度的初始缺陷下，最大增幅为78.7%～87.3%.

5)带钢板网壳对初始缺陷具有高度敏感性，同一矢跨比下，1/1 000～1/300比例初始几何缺陷下结构的极限承载力较无初始缺陷下结构的极限承载力分别降低 26.8% ～60.6%;另外，在1/8～1/5取值范围内，当矢跨比为1/7时，带钢板网壳对初始缺陷的敏感程度最高.

［1］周伟.新型煤气柜的强度和稳定性分析［D］.重庆:重庆大学，2004.

［2］黄斌，毛文筠.铺钢板肋环型网壳的稳定性研究［J］.空间结构，2007，13(4):7-10.

［3］曹力慧，宋延杰，郑建华，等.LNG储罐罐顶施工全过程分析的网壳结构优化设计［J］.化工设计，2012，22(5):35-37，40.

［4］李德昌，孙建刚，李建新.LNG储罐穹顶施工应力监测和数值模拟对比分析［J］.油气田地面工程，2012，31(10):33.

［5］邱菊.大型LNG全容储罐上部结构设计研究［D］.青岛:青岛理工大学，2011.

［6］豆文娇.大型LNG储罐拱顶结构应力分析［D］.兰州:兰州理工大学，2011.

［7］曹正罡.网壳结构弹塑性稳定性能研究［D］.哈尔滨:哈尔滨工业大学，2007.

［8］王焕定，王伟.有限单元法教程［M］.哈尔滨:哈尔滨工业大学出版社，2003.

［9］ZIENKIEWICZ O C，ZHU J Z.A simple error estimator and adaptive procedure for practical engineering analysis［J］.International Journal of Numerical Methods in Engineering，1987，24(2):337-357.

［10］金晓飞，李政，李景芳.广东台山核电站内安全壳穹顶施工阶段受力性能及稳定性分析［J］.建筑结构学报，2014，35(1):63-68.

［11］沈世钊，陈昕.网壳结构稳定性［M］.北京:科学出版社，1999.

［12］朱忠义，董石麟.单层穹顶网壳结构的几何非线性跳跃失稳及分歧屈曲的研究［J］.空间结构，1995，1(2):8-17.

［13］李元齐，沈祖炎.稳定分析中极值点失稳与分枝点失稳的跟踪策略及程序实现［J］.土木工程学报，1998，31(3):65-71.

［14］中华人民共和国住房和城乡建设部.JGJ 7—2010空间网格结构技术规程规定［S］.北京:中国建筑工业出版社，2010.