直接观测值回归与间接观测值回归方法的比较研究

□　别必鑫　魏世丽　余　哲

直接观测值回归与间接观测值回归方法的比较研究

□别必鑫1魏世丽2余哲3

（1.武汉市洪山区房管局测绘队，湖北武汉430070；2.阳泉市测绘处，山西阳泉 045000；3.太原理工大学测绘科学与技术系，山西太原030024）

在测量平差数据处理过程中，常涉及非线性函数模型。本文就可线性化的一元非线性回归模型进行研究，探讨了处理可线性化一元非线性回归模型的一种新方法—直接观测值回归方法。并以指数函数、幂函数和正态分布函数为例，逐一讨论了它们的间接观测值回归和直接观测值回归的线性化形式以及回归系数解的具体表达式。算例结果表明，本文提出的直接观测值回归方法比传统的间接观测值回归方法更为实用和有效。

直接观测值回归；间接观测值回归；方法比较

0.引言

回归分析是研究自然界变量之间存在的非确定性的相互依赖和制约关系，并把这种关系用数学表达式表达出来的一种方法，其目的是利用这些数学表达式以及对这些表达式的精确估计，对未知变量作出预测或检验其变化，为决策服务[1]。按照自变量和因变量之间的关系类型，回归分析可以分为线性回归分析和非线性回归分析。非线性回归分析作为社会科学定量研究方法中最基本的一种数据分析技术，在测绘学、计量学、地理学等诸多领域得到了广泛应用。在常用的非线性回归模型中，大部分可以通过适当的数学变换转换成线性回归模型来进行参数估计，称这类模型为可线性化模型。有些非线性模型则无法通过数学变换的方式转换成线性模型，称这类模型为不可线性化模型。

1.直接观测值回归和间接观测值回归

可线性化的一元非线性回归模型的基本处理思路是通过数学变换将非线性模型转换成线性模型，然后用最小二乘法（LS法）计算回归系数[2]。将非线性模型转换成线性模型有两种回归方法：一种是经过线性化后，以间接观测值，即直接观测值的函数作为因变量，这是传统的方法，称其为间接观测值回归；另一种是经过线性化后，以直接观测值作为因变量，这是本文将要讨论的方法，称其为直接观测值回归。

间接观测值回归是将一元非线性回归转换为一元线性回归的常用方法，其所得到的改正数是观测值函数的改正数，而直接观测值回归得到的改正数是观测值的改正数。

2.直接观测值回归和间接观测值回归的计算

以指数函数、幂函数和正态分布函数为例，来说明直接观测值回归和间接观测值回归的计算。

2.1指数函数

函数模型为

回归方程为

间接观测值回归的线性化形式为

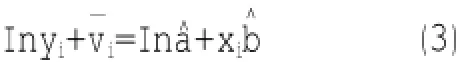
式中，vi是因变量Inyi的残差。

直接观测值回归的线性化形式为

式中， vi是yi的残差。

第一项用泰勒展开，得

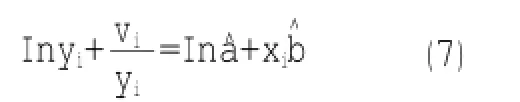
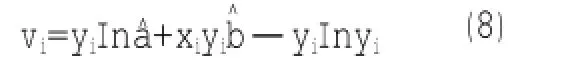
用LS法得到回归系数和的解：

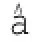
2.2幂函数

函数模型为

回归方程为

间接观测值回归的线性化形式为

式中，vi是因变量Inyi的残差。

直接观测值回归的线性化形式为

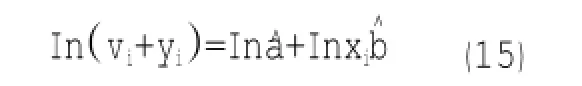
第一项用泰勒展开，得

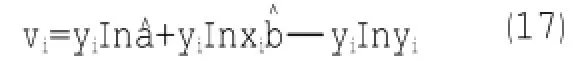
2.3正态分布函数

函数模型为

回归方程为

间接观测值回归的线性化形式为

式中，vi是因变量Inyi的残差。

直接观测值回归的线性化形式为

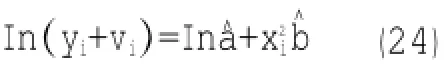
式中，vi是因变量yi

的残差。

第一项用泰勒展开，得

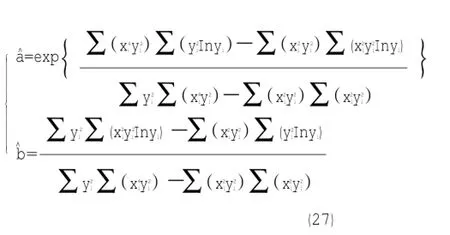
3.直接观测值回归和间接观测值回归的算例比较及结果讨论

以指数函数为例，对其直接观测值回归和间接观测值回归的算例结果进行比较与讨论。

理论回归系数：a=12.5，b=0.5。

用三组不同大小的自变量XA、XB和XC分别计算三组因变量的真值YA、YB和YC。三组因变量YA、YB和YC的区别在于，因变量YA之间的数值差异较小，因变量YB之间的数值差异适中，因变量YC之间的数值差异较大。模拟一组观测值的真误差Δ，进而用YA、YB和YC分别加真误差Δ得到模拟观测值LA、LB和LC，分别见表1、表2和表3。分别用间接观测值回归和直接观测值回归对每一组模拟观测值进行计算，模拟观测值之间数值差异较小的计算结果见表1，模拟观测值之间数值差异适中的计算结果见表2，模拟观测值之间数值差异较大的计算结果见表3。残余真误差和残余真误差均方误差的计算方法见参考文献[3]。

表1　指数函数观测值之间数值差异小时两种方法的比较

表2　指数函数观测值之间数值差异中时两种方法的比较

表3　指数函数观测值之间数值差异大时两种方法的比较

续表

对于观测值之间数值差异较小的情形（表1），间接观测值回归的残余真误差均方误差为0.32，直接观测值回归的残余真误差均方误差为0.30，两者的回归结果差异不显著。对于观测值之间数值差异适中的情形（表2），间接观测值回归的残余真误差均方误差为0.33，直接观测值回归的残余真误差均方误差为0.28，两者的回归结果具有一定的差异。对于观测值之间数值差异较大的情形（表3），间接观测值回归的残余真误差均方误差为0.52，直接观测值回归的残余真误差均方误差为0.17，两者的回归结果差异十分显著。

另，对于幂函数和正态分布函数，也都具有类似的结论。

因此，直接观测值回归的结果优于间接观测值回归的结果，特别是当观测值之间数值差异较大时。

4.结论

本文讨论了一元非线性回归的直接观测值回归方法。对于可线性化的一元非线性回归模型，传统的处理方法是采用间接观测值回归，即以直接观测值的函数作为因变量；而本文探讨的直接观测值回归是以直接观测值作为因变量。直接观测值回归和间接观测值回归具有相同形式的函数模型和回归方程，然而它们的线性化方式不同，线性化方式的差异导致了这两种回归方法结果间的差异。算例结果表明，当观测值之间的数值差异较小时，间接观测值回归的结果近似于直接观测值回归的结果；当观测值之间的数值差异较大时，间接观测值回归的结果和直接观测值回归的结果有很显著的差异，且直接观测值回归的结果优于间接观测值回归的结果。无论观测值之间的数值差异是小还是大，直接观测值回归都有更好的回归结果。因此，本文探讨的直接观测值回归方法比传统的间接观测值回归方法更实用有效。研究结果可为可线性化的非线性回归模型进行线性化处理时有效地选取回归方法提供借鉴和参考，同时对于提高一元非线性回归模型系数的质量具有一定的实际应用价值。

【1】葛永慧.再生权最小二乘法稳健估计[M].北京:科学出版社,2015.

【2】别必鑫,魏世丽.一元非线性回归方程系数的通解[J].经纬天地,2014,(6):55-59.

【3】Ge,Y.;Yuan,Y.;Jia,N.More efficient methods among commonly used robust estimation methods for GPS coordinate transformation[J].Survey Review,2013,45(330):229-234.

O241.7

A

2095-7319（2015）06-0051-05

别必鑫（1963-），男，高级工程师，武汉市洪山区房管局测绘队，毕业于武汉大学测绘学院，主要从事工程测量工作和房产测绘工作。