基于改进GA的分段堆场计划调度方法研究

张志英，计峰，曾建智

(同济大学机械与能源工程学院，上海200092)

分段是船体建造的基本单位，通常一艘船由上百个分段组成。分段在舾装、喷漆等工艺处理后需到分段堆场进行预舾装、检验和修补等作业或暂存。脱胎后的分段质量几十至几百吨。对进场分段，需安排一个空的作业场地和一条可行的路径。由于分段尺寸和质量很大，吊车无法对其进行垂直方向上的运输，因而只能在平面上通过平板车运输，一次仅可装一个。运输道路上若存在分段挡道，应先将阻挡分段移至空地，待平板车运输完目标分段后，再将阻挡分段移回原处。在实际堆场作业中，如何有效降低移动成本显得尤为重要。

分段堆场在生产运作中受各种干扰因素影响，如分段优先权关系变动、分段在堆场内作业时间变动等，因此需要根据系统状况进行分段计划的重调度，以确保分段调度的顺利进行。重调度既避免了实时调度中不考虑全局最优的缺陷，又避免了预测调度中冗余时间的浪费，是一种兼顾全局和效率的折中方案。关于重调度问题的研究主要集中在单台机器、并行机器、流水车间和作业车间的重调度方法、重调度对动态制造系统性能的影响等方面［1］。Parviz等研究了在时间冲突情况下的柔性作业车间重调度方法［2］。Sabuncuoglu等探索了机器可靠性较差条件下的柔性作业车间重调度［3］。李铁克等研究了在机器故障情况下混合流水车间的重调度［4］。

船舶分段堆场调度问题需考虑储位分配、路径及计划分段的调度顺序等，这与车辆调度问题有相似之处。Jemai等以优化能源为目标，利用NSGA II算法研究了车辆调度问题［5］。Psychas等利用多星NSGA II算法对多目标的车辆调度问题进行求解［6］。Spliet等利用二阶段启发式算法对能力约束的车辆重调度问题进行了求解［7］。

国内外针对船舶分段堆场调度问题的研究较少。Changkyu等以临时分段移动量最少为目标建立优化模型，提出遗传算法和改进动态启发式算法对模型进行求解［8-9］。然而这些方法都限定分段必须按直线进出堆场，增加了临时分段移动量。考虑到提升堆场柔性的必要性，申钢等以临时分段移动量最小为目标建立最短路模型，提出分支定界法和启发式规则来确定分段移动路径和停放位置［10］。徐建祥等提出临时场地用于暂时停放临时移动分段，利用遗传算法确定分段在堆场中停放位置的最优方案，并构建启发式规则来确定分段在堆场中的最优进、出场路径［11］。

本文综合考虑随机扰动、分段质量、场地柔性及堆场形状等影响因素，以总移动成本最小为优化目标，运用改进遗传算法和启发式规则对分段堆场调度问题进行建模。合理安排分段进出堆场顺序，确定分段在堆场中的最优停放位置，规划其进、出堆场的路径，从而优化堆场资源的利用率，提高堆场周转率。结合某大型船厂实际生产数据进行验证，得出存在随机扰动下的调度方案，结果表明该方案更符合船厂堆场调度的实际情况。

1 问题描述与解决方法

1.1 问题描述

堆场是分段脱胎后进行后处理或暂存的作业场所。堆场计划分段可分为进场分段和出场分段。分段在进入或移出堆场的过程中，如有分段堵塞通道，则需将挡道分段先移至别处，等分段到达目的位置后，挡道分段可回归原位、重新选位和移至临时暂存场所。重新选位和移至临时暂存场所虽一定程度上降低了移动成本，但前者给分段的定位和查寻带来不便，后者则占用更多场地资源。分段移动成本主要在平板车的油耗和损耗。分段质量是影响平板车油耗和损耗的关键因素。平板车运输分段分3个过程:装载、运输分段至目的地、卸载。不考虑驾驶员操作水平，天气等因素，同质量分段运输同等距离所需油耗几乎相等。分段路径不唯一，造成不等的分段移动成本。

在复杂多变的船舶堆场生产环境下，各种扰动的随机发生导致了堆场运作的不确定性。本文主要讨论分段延期出场、紧急插单和分段优先权关系变动这3类扰动因素。分段延期出场和紧急插单导致后续分段的调度环境因空余作业场地减少而发生变化，影响了初始的全局调度。分段优先权关系变动对变动分段调度期内的环境造成改变。这些随机扰动因素影响了船舶堆场的生产进度，严重阻碍了堆场物流系统的正常运行，因此有必要对影响物流系统性能的各种扰动进行重调度。

对船舶分段堆场的作业过程进行研究，考虑到调度的实际情况及求解计算方便，作以下假设:1)堆场由若干大小相等的正方形场地组成;2)分段用最小包络矩形近似;3)一个作业场地只能放一个分段，一个分段只能放在一个作业场地上;4)各装卸设备正常运行。要解决的问题有:1)确定进场分段在堆场中合适的停放位置;2)确定分段进出堆场的最佳路径。

1.2 解决方法

船舶分段堆场调度需要在满足分段后续作业需求的前提下，充分考虑调度周期内所有计划分段进出堆场的顺序对分段停放位置的影响，并要规划好分段路径。本文通过对调度分段所产生油耗的历史数据统计分类，得到质量-距离-成本模型，以总移动成本最小化为目标，对于调度周期内的进场分段，利用改进遗传方法为其安排停放位置，规划其在堆场中的路径。对于出场分段则只需根据其停放位置规划出场路径即可。

2 建立船舶分段堆场调度模型

2.1 堆场状态矩阵的建立

为表达分段在堆场中的停放位置以及堆场中作业场地的状态，建立图1所示的堆场状态矩阵。图1表示的是五行九列作业场地的堆场，矩阵元素aij为场地状态，其值为0或1，1表示某作业场地上已放有分段，否则为0。

图1 堆场状态矩阵Fig.1 Yard state matrix

2.2 质量-距离-成本模型

在平板车运输过程中，分段质量越重，移动路程越长，平板车油耗越高，相应的成本也就越大。对于同质量分段，装载、运输和卸载过程所需油耗与分段的形状、驾驶员熟练度、道路湿度有关，物理学公式计算获取油耗并不适用。本文以10 t作为单位质量，以单个作业场地的边长15 m作为单位距离，通过追踪各个分段运输油耗并对同质量区间同距离的油耗历史数据进行取平均值处理，得到分段的质量-距离-成本模型，如表1所示。模型为

式中:Ai为待调度的第i个分段;mi表示分段Ai的质量;Vij表示从上至下，从左至右第i行第j列作业场地;Cij为分段从Vij移至道路所需成本;O(mi，Ri)表示质量为mi的分段到道路最优距离Ri对应的油耗;f0为当前油价。

表1 质量-距离-成本模型表Table 1 Weight-distance-cost model

2.3 重调度驱动规则

周期性调度是按照系统事先安排的调度周期进行周期性重调度，对系统缺乏应对各种扰动的快速响应能力。而事件驱动规则是针对突发事件所采取的调度策略，即当堆场在生产过程中有突发事件出现，为响应这些事件，而必须立即进行重调度。通过采用基于事件驱动的再调度策略，调度系统可以较好地响应实际的动态环境，保持一定的稳定性，是实现动态调度的一个较好的策略。例如，当某分段的质量不满足验收标准时，启动重调度，将序号位于该分段前的所有分段按原计划继续调度，而剩余的分段构成重调度优化集，根据新的调度顺序进行重调度。

2.4 船舶分段堆场调度模型

2.4.1 概念定义

为了更好的理解模型，做如下定义:

计划分段:T周期内需要进行操作的分段。挡道分段:由于挡道需临时移出，最后又移回原位的分段。分段移动成本:调度目标分段所需的移动成本，包括目标分段和挡道分段。总移动成本:所有计划分段的分段移动成本之和。

2.4.2 数学模型的建立

堆场作业计划以总移动成本最少为优化目标，对于进场分段，可以将停放位置看作起始点，从停放位置处寻最优路径来简化模型。参数设定如下:

A=((A1，m1)，(A2，m2)…，(Ai，mi)…，(An，mn))为T周期内待调度计划分段集，i=1，2…，n;;Ei为分段Ai开始调度时，堆场状态矩阵中“0”的个数;(L，W)为作业场地的尺寸，取L=W=15 m;(Li，Wi)为分段Ai的投影参数;Ri为分段Ai到道路的最优距离;Qi为靠近道路端的第i行作业场地;S=(S1，S2…，Sk…，Sm)为堆场内的场地集，k=1，2…，m;Vr为道路对应的节点;Bi为周期内第i个进场分段，i=1，2，…，n;B0ij为堆场中第i行，第j列计划出场的分段;B-k为周期内第k个进场分段在此周期内出场;

［ts，tf］为 T 周期的始末时刻;［tis，tif］为Ai的计划周期;P=(P1，P2，…，Pk，…，Pz)为T周期内因事件触发而导致计划上出现异常的分段集(按初始计划中的顺序依次排列);h为若分段P1需延期进出场，则h表示其在初始计划中的序号;若P1需提前进出场，则h表示其在重调度计划中的序号;Uk为分段Pk的触发时刻;trs为分段Pk重调度后的计划进或出场时刻，rs=1，2…，n;S0为单个作业场地的面积;根据质量-距离-成本模型建立以移动成本最小为优化目标的函数:

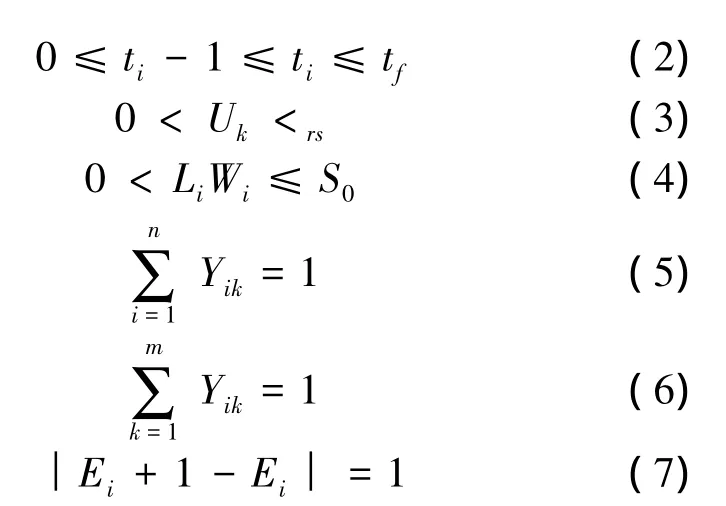
该模型综合考虑随机扰动、分段质量、场地柔性和堆场布局等因素，以总移动成本最小为优化目标。函数(1)逐个计算并确定每个分段的最优路径，得出该方案产生的最少总移动成本。运用改进遗传算法操作在所有方案中选出最优方案来安排堆场计划;约束条件(2)限制分段的出场时间要在T周期内;约束条件(3)说明需要时间重排异常分段;约束条件(4)保证作业场地能容下放置的分段;约束条件(5)限定一个作业场地只能放一个分段。约束条件(6)确保一个分段只能放置在一个作业场地上。约束条件(7)说明相邻的调度分段之间的堆场状态必定不同。

2.5 改进遗传算法

遗传算法的参数中交叉概率Pc和变异概率Pm的选择是影响遗传算法行为和性能的关键所在，直接影响算法的收敛性。本文采用Srinvivas提出的一种自适应算法，Pc和Pm能够随适应度大小自动改变［12］。对于适应度高于群体平均适应值的个体，相对应于较低的Pc和Pm，使该解得以保护进入下一代;而低于平均适应值的个体，相对应于较高的Pc和Pm，使该解被淘汰。Pc和Pm按如下公式进行自适应调整:

式中:fmax为群体中最大的适应度值，favg为每代群体的平均适应度值，f'为要交叉两个体中较大的适应度值，f为要变异个体的适应度值。取适应度函数:

3 模型求解

3.1 编码和解码

对于进场分段在堆场中可能放置的作业场地位置，依据数学组合原理，把每种不同的放置组合形成一种调度方案，即为一个染色体。

1)编码:染色体的长度是待调度分段数目，其基因排列顺序就是分段的调度顺序。每个基因是一个二维数组，对于进场分段，前者的值表示从上至下，从左至右第n个0作为停放位置，对于出场分段，则表示其所在位置。数组后者的值是计划分段的质量。现根据图1编制一染色体，如图2所示。

图2 染色体示例Fig.2 An example for chromosome

基因序号1～6依次是计划分段的调度顺序。3、6号是出场分段(其他为进场分段)，3号的045代表其在V45，221代表质量，6号的-2表示计划分段中第2个进场分段在周期内出场。1号的3代表选择第3个空作业场地作为停放位置。

2)解码:计算每个分段的分段移动油耗。具体过程如下:

现在，农村相继成立了合作社，农民开始有计划地科学种地。不需要乡镇干部瞎指挥了。全乡除了农科站、计划生育办还有点事外，其他人闲来无事，白天不是找借口划拉个体户，就是巧立名目大量开垦生活基地种经济作物；晚上，喝酒，打麻将——

①建立堆场初始节点质量状态模型，如图3所示。

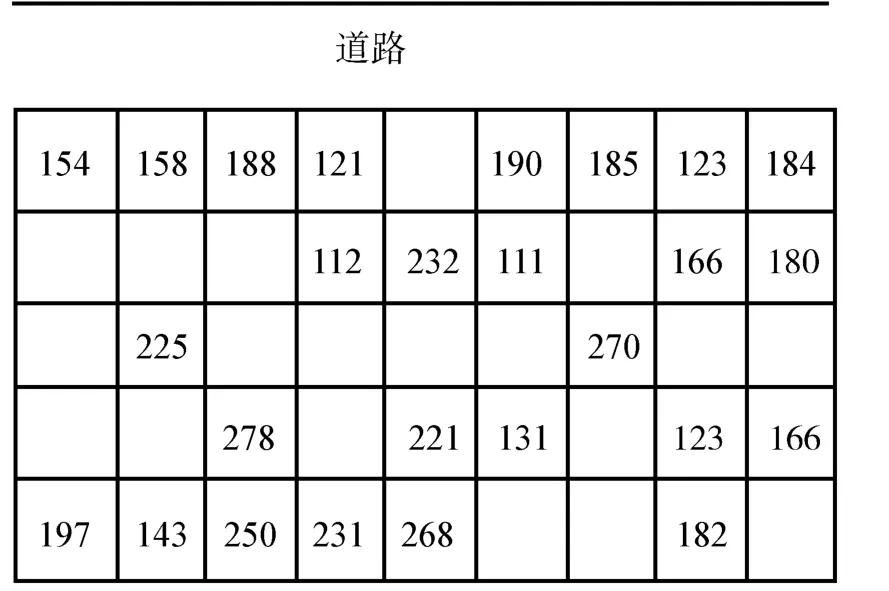
图3 堆场初始状态图示例Fig.3 Example of yard initial state

②运用动态规划:a.Q1～Q5逐行向上搜索得到节点信息:有无分段、分段质量、路径距离、最优路径、油耗(含挡道分段);b.搜索分向上、向左、向右3种。从Q2行左边开始向左搜索相邻节点的油耗，遇到挡道分段则按其最优路径距离加分段到挡道分段的距离之和作为最短路径，求此路径下油耗与挡道分段油耗之和;向右搜索同理，取三者的最小值作为分段移动油耗，并更新节点的最优路径，路径距离;c.Q3～Q5同Q2，求出各行各节点信息。

③若是出场分段，则直接获得分段所在位置的分段移动油耗;若是进场分段，则将停放位置的质量信息修改从而更新整个堆场的节点状态，即可得到停放位置的分段移动油耗信息，乘以油价即为分段移动成本。每完成一个分段计划，堆场节点信息相应的更新一次。

④根据式(1)对进出场各分段的分段移动成本求和，计算该方案下的总移动成本。

3.2 进化

采用精英保留战略，即把适应度好的个体保留下来，并利用其好的性质来繁殖后代。同时采用比例选择算子，使个体按照与适应度成正比的概率向下一代群体繁殖。设某染色体的适应度为Pi，则其被选择的概率为Pi/∑Pi。采用多点交叉，对于选中的用于繁殖的每一对个体，随机地产生与个体长度相同的染色体O(所有基因值为0或1)，将双亲的基因，在染色体O的基因中基因值为1对应的位置处相互交换。现有个体X、Y，根据交叉规则，在随机染色体O的基因中值为1处交叉产生新个体X'、Y'，它们组合了父辈个体的特征，如图4所示。变异方式是先以一定概率从种群中选择一个个体，再随机生成一个染色体。个体将在随机染色体中所有基因值为1处对应的位置上，用另一随机产生的序号代替它(若是出场分段则不变)。但要注意的是随机产生的序号必须在1～n中产生，n是进场分段当前堆场状态矩阵中0的个数上限。例如可从1～5中选取1代替图5中X染色体的第2个基因值5。染色体变异如图5所示。

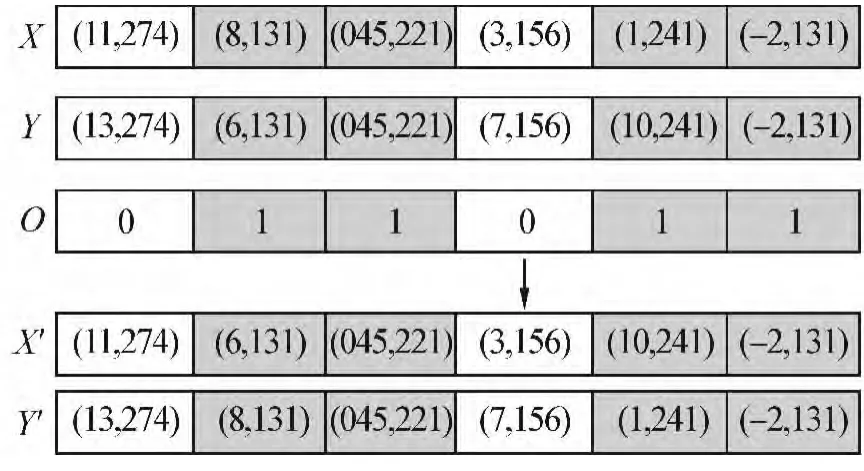
图4 染色体交叉图Fig.4 Crossover of chromosome

图5 染色体变异图Fig.5 Mutation of chromosome

3.3 重调度

调度过程中若有扰动事件发生，则抽取出所有因扰动事件触发而导致调度顺序出现异常的分段，并根据生产具体情况将这些分段与待调度分段一起进行顺序重排，然后重复步骤1)、2)，得到重调度计划。

4 实例验证与分析

4.1 实验验证与结果

为验证所建模型及算法的可行性与正确性，以上海某大型船厂1周内的船舶分段堆场计划调度为例，利用JAVA软件，在处理器为2 GHz，内存为4 GB的计算机上进行求解。实验包括以下输入参数:1)堆场尺寸及当前的使用状况，即初始状态;2)一个周期内，进出场分段的计划数量、计划顺序及计划时间;3)遗传算法参数设置如下:种群规模为100，个体长度为 37，交叉概率Pc1=0.9，Pc2=0.6，变异概率Pm1=0.1，Pm2=0.001，算法终止代数为 50。某堆场的初始状态如图6所示，0代表该作业场地没有分段占用，非0数字代表放在该作业场地的分段质量，图中共有10个空作业场地。

按时间顺序排列的一周内堆场作业计划如表2，序号26出场分段B-2的所在位置V5表示它由序号5的进场分段决定。

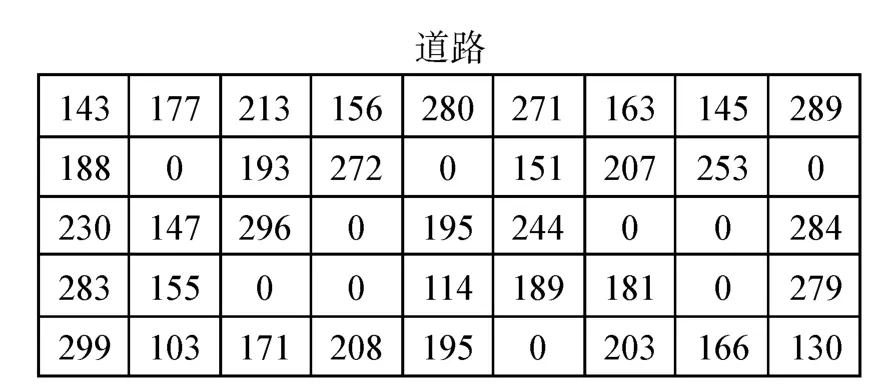
图6 堆场的初始状态Fig.6 Yard initial state

表2 一周内堆场计划Table 2 Yard plan for one week

通过算法程序确定进场分段在堆场中的停放位置以及进出场分段从停放位置到道路Vr的路径，得到一种较优的堆场调度方案如表3所示。随着程序的运行，个体的多样性在第17代后逐渐消失，解开始收敛，收敛时间为1.224 s，收敛曲线如图7所示。

为验证重调度方法的有效性，以质量检验不合格导致分段推迟出场及订单加急分段提前进场两类扰动事件触发重调度系统。现基于预测控制技术预知序号22的分段B047因质量验收不合格而需要延期，在序号29的分段B14进场后出场。序号33的分段B035因订单加急在序号25的分段B13进场后出场。结合滚动时域重排分段的调度顺序，并按时间顺序进行二次重调度，结果如表4所示(表中灰色表示分段重排后的新顺序)。

表3 堆场计划调度方案Table 3 Stockyard plan scheduling scheme

图7 改进遗传算法收敛曲线Fig.7 Convergence curve of improve genetic algorithm

表4 堆场重调度方案Table 4 Yard rescheduling solution

4.2 数值分析

4.2.1 堆场尺寸及初始利用率的比较分析

进场分段不同放置位置的组合以及进出场路径的选择造成了船舶分段堆场调度问题的复杂性。表5显示，总成本及收敛时间随着堆场尺寸和计划分段数的扩大而增加;相同尺寸的堆场，在相同计划分段数的调度下，初始利用率高的总成本比初始利用率低的高，程序运行时间反之，这是由于初始利用率低的堆场少了挡道分段，进出场分段相应的移动成本变低，且可行解规模大;堆场的行数比列数对实验结果影响更大。

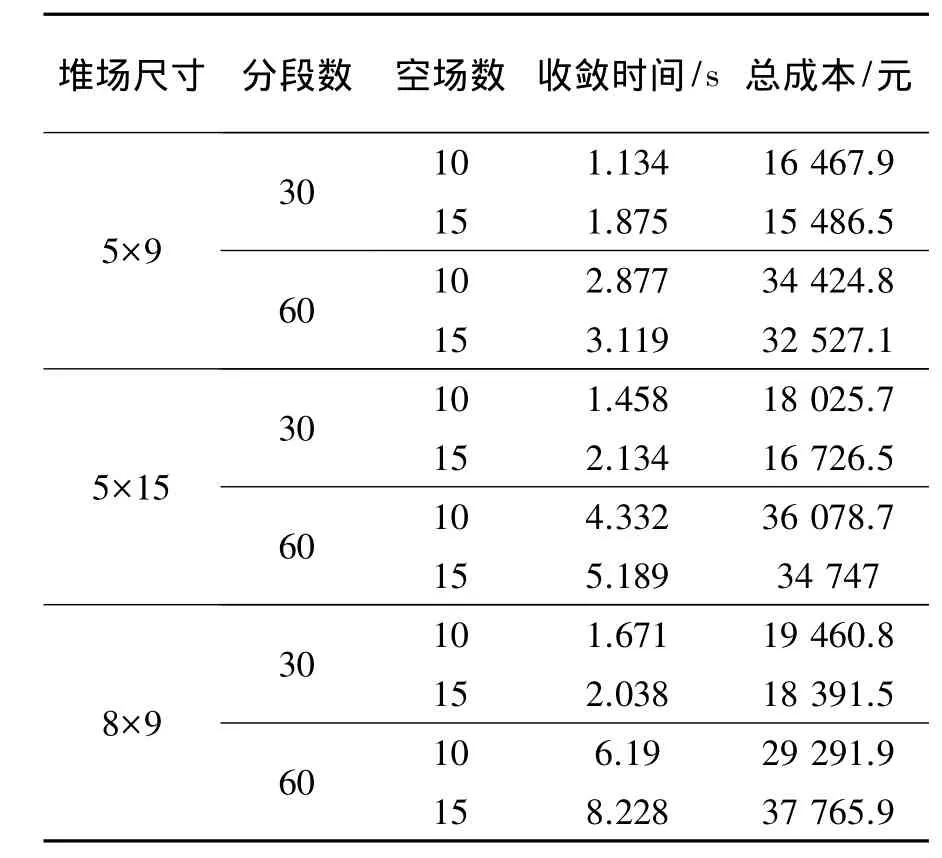
表5 不同参数的对比结果Table 5 Comparison of different factors

4.2.2 算法比较分析

分段进出场路径的选择使堆场调度问题复杂性增强。对于路径的求解可以通过Dijkstra算法来优化，Dijkstra算法是典型最短路算法，主要特点是以起始点为中心向外层扩展，直到扩展到终点为止，而此问题包含距离和质量2个因素，故只知相邻分段的质量而无法直接得到分段移动成本，需遍历可能的路径再逐个计算以获得最优路径。本文将整个路径选择过程划分为几个阶段子过程再利用动态规划逐个获得移出分段的最小成本，从而简化路径选择过程。利用JAVA软件，在处理器为2.0 GHz，内存为4 GB的计算机上实现改进Dijkstra算法求解分段移动路径。并将改进Dijkstra算法与动态规划进行对比，结果如表6所示。可以发现:随着堆场规模的增大，2种算法的耗时都逐渐地提高，但后者的运行时间明显小于前者，并且堆场尺寸越小，动态规划算法较改进Dijkstra算法的优越性就更突出。

表6 算法比较分析Table 6 Comparison of algorithms

5 结束语

通过对船舶分段堆场的调度过程进行研究，综合考虑了扰动事件、分段质量、初始利用率、计划分段个数、堆场尺寸等因素，通过建模并采用遗传算法及改进的启发式规则对其进行求解。仿真实验结果验证了方法的有效性和实用性。由于研究基于较多的假设，没有考虑实际船厂运作中平板车、龙门吊的可用性约束及分段进出堆场的时间约束问题，需要进一步研究。

［1］李莉，乔非，吴启迪.半导体制造重调度研究［J］.中国机械工程，2006，17(6):612-616.LI Li，QIAO Fei，WU Qidi.Research on rescheduling for semiconductor wafer fabs［J］.China Mechanical Engineering，2006，17(6):612-616.

［2］FATTAHI P，JOLAI F，ARKAT J.Flexible job shop scheduling with overlapping in operations［J］.Applied Mathematical Modelling，2009，33(7):3076-3087.

［3］SABUNCUOGLU I，KARABUK S.Rescheduling frequency in an FMS with uncertain process times and unreliable machines［J］.Journal of Manufacturing Systems，1999，18(4):268-283.

［4］李铁克，肖拥军，王柏琳.基于局部性修复的HFS机器故障重调度［J］.管理工程学报，2010，4(3):45-49.LI Tieke，XIAO Yongjun，WANG Bolin.HFS rescheduling under machine failures based on local repair［J］.Journal of Industrial Engineering and Engineering Management，2010，4(3):45-49.

［5］JEMAI J，ZEKRI M，MELLOULI K.An NSGA-II algorithm for the green vehicle routing problem［M］//HAO J K，MIDDENDORF M.Evolutionary Computation in Combinatorial Optimization.Berlin:Springer，2012:37-48.

［6］PSYCHAS I D，MARINAKI M，MARINAKIS Y.A parallel multi-start NSGA II algorithm for multiobjective energy reduction vehicle routing problem［C］//Evolutionary Multi-Criterion Optimization.Springer，2015:336-350.

［7］SPLIET R，GABOR A F，DEKKER R.The vehicle rescheduling problem［J］.Computers ＆ Operations Research，2014，43(3):129-136.

［8］PARK C，SEO J.Mathematical modeling and solving procedure of the planar storage location assignment problem［J］.Computers＆ Industrial Engineering，2009，57(3):1062-1071.

［9］PARK C，SEO J.Comparing heuristic algorithms of the planar storage location assignment problem［J］.Transportation Research Part E:Logistics and Transportation Review，2010，46(1):171-185.

［10］张志英，申钢，刘祥瑞，等.基于最短路算法的船舶分段堆场调度［J］.计算机集成制造系统，2012，18(9):1982-1990.ZHANG Zhiying，SHEN Gang，LIU Xiangrui，et al.Block storage yard scheduling of shipbuilding based on shortestpath algorithm［J］.Computer Integrated Manufacturing Systems，2012，18(9):1982-1990.

［11］张志英，徐建祥，计峰.基于遗传算法的船舶分段堆场调度研究［J］.上海交通大学学报，2013，47(7):1036-1042.ZHANG Zhiying，XU Jianxiang，JI Feng.Shipbuilding yard scheduling approach based on genetic algorithm［J］.Journal of Shanghai Jiaotong University，2013，47(7):1036-1042.

［12］SRINIVAS M，PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms［J］.IEEE Transactions on Systems，Man，and Cybernetics，1994，24(4):656-667.