基于GPU并行的改进SPH方法对粘性流场的模拟

金善勤，郑兴，段文洋

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

光滑粒子水动力学(smoothed particle hydrodynamics，SPH)方法是一种无网格的拉格朗日粒子算法，其目前已成为水动力学中数值模拟的主要方法之一。1994年Monaghan［1］首先将光滑粒子水动力学方法(SPH)应用于自由表面流动的模拟，基于弱可压缩流体假设引入状态方程，以二维溃坝模型为研究对象，讨论了SPH方法在计算水动力学问题中的可行性。随后，Colagrossi等［2-3］采用 SPH方法，对任意形状物体入水后的自由表面形状及强非线性效应进行了研究。

传统SPH方法在压力计算和物理粘性模拟等方面存在不足，国内外许多学者对其进行了改进。Monaghan等［4］为了减少粒子在运动中出现的非物理震荡，防止粒子在运动过程中由于距离太小而发生非物理穿透，其在动量方程中加入了人工粘性修正项。针对弱可压缩SPH方法在压力求解过程中出现的不稳定现象，Marrone等［5-6］基于黎曼解的压力修正思想提出了δ-SPH方法，并以二维溃坝问题为研究对象，证实了该方法的有效性。国内的许多学者也在SPH算法改进方面进行研究，高睿等［7］采用黎曼求解N-S方程，改进了SPH方法，并研究了规则波与结构物的相互作用，郑兴等［8-9］针对传统SPH方法二阶核近似后存在精度不高的问题，提出了改进的K2_SPH方法，并将其应用于强非线性自由表面问题的研究。

由于传统SPH方法计算效率不高，提高 SPH计算效率也是研究人员关注的一个重点。采用GPU加速SPH算法是近几年来发展的一种新的SPH方法计算模式。借助于GPU的众核优势，对SPH算法并行优化，能够显著的提高计算效率。目前国内外许多研究人员已经在该方面取得了一些成果，例如Xiong等［10］采用自适应粒子分裂和合并技术在单GPU和多GPU上分别实现了SPH方法的并行计算，徐锋等［11］对SPH方法在GPU上的物理存储模式和线程使用方式进行了较为详细的论述，朱小松等［12］对GPU和CPU上的MPS方法和SPH方法的并行计算进行研究，并借助此方法对液舱晃荡问题进行了分析。虽然目前基于GPU的SPH算法发展迅速，但是仍然存在一些问题有待解决，如并行计算模式单一、压力计算结果不稳定等。

针对以上不足，本文提出一种基于粒子对的并行计算方法，并将其与δ-SPH方法结合，通过对粘性流场的模拟，研究不同边界处理方法对计算结果的影响，不同粒子加速方法对计算精度和加速效果的影响。

1 SPH的基本理论

SPH方法是一个在粒子系统中进行插值的计算方法，流域被离散成许多的有限体积单元，这些有限体积单元即为粒子。每个粒子点都具有自身的物理属性如:质量、密度、速度等。在i粒子处的场函数和场函数的梯度可用核近似的形式来表示:

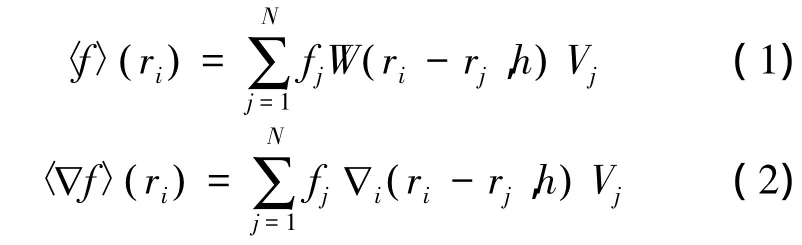
式中:h为光滑长度，N为i粒子支持域内的相邻粒子数，fj表示j粒子点的场函数值，Vj表示j粒子的体积，W ri-rj，h

( )表示核函数值。当支持域半径趋向于0时，核函数W ri-rj，h( )便变成了狄拉克函数。

2 δ-SPH的控制方程

δ-SPH方法是在传统SPH方法的基础上，基于密度修正和黎曼解的压力修正思想提出的一种改进SPH方法，其控制方程可描述为

式中:p、ρ、v分别表示粒子点的压力、密度、速度;f为外力项;σ为总应力张量，由压力p和粘性应力τ组成;α、β表示坐标方向。

对于牛顿流体，粘性剪切应力和剪切应变成正比，于是有

式(3)中，Ψij和πij分别为密度修正项和人工粘性项，h为平均光滑长度，c为平均声速，ω和ε分别为密度修正项和人工粘性项系数。Ψij表达式为

其中，

采用SPH方法模拟粘性流场的流动既是一个边值问题，又是一个初始条件问题。采用不同的边界处理方法，会对计算的精度和稳定性造成不同的影响。所以，有必要对边界处理方法进行相应的研究，寻找最优的边界处理方法。目前常用的边界处理方法有:基于排斥力的固壁粒子方法、镜像粒子边界处理方法和周期性边界处理方法，关于其详细介绍请参考文献［13］。

3 基于粒子对的GPU并行算法

借助GPU的众核架构优势，加速SPH算法是近年来发展的一种全新的计算方法。传统SPH方法良好的并行特性，为该方法能够顺利在GPU上的实现并行计算提供了基础。此外相比于完全不可压缩SPH(ISPH)，本文采用的δ-SPH方法与传统SPH方法一样具有良好的并行特性。目前基于GPU的SPH算法大多采用基于单个粒子的并行计算模式，单个线程计算单个粒子的流体控制方程，得到单个粒子点的密度变化率和加速度等信息。在GPU的单指令多线程(SIMT)并行模式下，多个线程可同时发射、同时运行，由于SPH方法各个粒子之间不存在较强的相关性，这样多个粒子可同时在GPU上开展并行计算，关于该方面的详细介绍可参考文献［11，14］。研究表明随着粒子数量的不断增加，采用基于单个粒子并行方法的加速能力提高缓慢。为此，本文提出了一种基于粒子对的并行计算方法，该方法的全部计算任务都在GPU上完成，中间计算过程不需要进行GPU和CPU的数据传递，因此该方法的计算效率得到了较大提高。图1给出了采用基于单个粒子和粒子对2种不同并行计算方法的加速比随着粒子数量变化的曲线。由图1可得，采用基于粒子对的并行计算方法优势明显。传统SPH计算方法大多采用逐个求解单个粒子控制方程的计算模式，Riffert等［15］提出了成对相互作用法，通过分析粒子的成对相互作用，可以较大的提高粒子的计算效率和存储空间。

图1 加速比随粒子数增加的变化曲线Fig.1 Speed ratio curve along with increase of the particle number

在CUDA架构下，每个线程块中的线程都有系统赋予其唯一的标识符［16］。虽然不同计算能力的GPU所能使用的最大线程数量不同，当在所有流处理器都被占满时，由于计算指令处于等待模式，这样使得粒子数量再多，同样可以使得每个线程和粒子对编号一一对应。计算开始时，由CPU主机端将流场粒子的初始物理信息全部拷贝至GPU设备端，根据δ-SPH的求解顺序，每个线程控制对应粒子依次进行粒子对查找，密度计算，修正项密度计算，加速度计算等。然后采用跳蛙法求出下一步的流场初始信息，不断循环至流场达到稳定状态，基于粒子对的并行计算流程如图2所示。

在GPU上大量的晶体管被用于执行单元，而不像CPU那样作为控制单元和缓存，因此GPU对选择、循环等分支结构的处理能力并不如CPU那样出色。在SPH算法中，边界处理和邻近粒子的查找需要许多分支语句，因此，这类操作在整个并行过程中耗时最多。为了提高计算效率，本文2种并行算法均采用基于网格哈希值的链表搜索方法，关于其详细介绍请参考文献［14］。

采用粒子对并行计算方法时，多个线程在不同流处理器中对相应的粒子对进行计算，此时会存在多个线程同时对某一粒子的变量内存进行读取和写入操作的情况，这样会导致数据叠加错误，必须对线程操作进行排序，才能得到正确的计算结果。为了保证每个线程操作结果的正确，本文采用了原子操作。原子操作能够控制对同一变量内存进行读取写入操作的线程数量，使得基于粒子对并行模式的GPU计算方法得以实现。

图2 基于粒子对的GPU并行流程Fig.2 GPU parallel process based on particle pair

4 数值模拟和分析

4.1 多种边界处理方法的比较

4.1.1 腔内剪切流动问题数值模型

腔内剪切流动是一种经典的流体运动，流体放置在正方形容器内，容器的顶部平板以恒定速度vtop做水平运动，容器的其余三边为固定边界，通过顶部边界的运动来驱动容器内流体的运动，流场稳定时能在靠近顶部处形成回流［17-18］。这一计算模型能够较好地检验SPH算法对运动边界和固定边界的处理。计算数值模型相关参数为:正方形容器边长l=0.001 m ，顶部边界速度vtop=0.001 m/s，动粘系数ν=10-6m2/s，密度ρ=103kg/m3。在此情况下雷诺数为1。在正方形容器内分布有1 600(40×40)个粒子，分别采用基于排斥力的固壁粒子边界处理法、镜像粒子处理法、固壁粒子加镜像混合处理方法3种不同方法对正方形边界进行处理。

4.1.2 腔内剪切流数值结果与分析

在模拟腔内剪切流动问题时，压力状态方程的c0取0.01，固壁粒子半径取初始粒子间距的一半。图3为采用不同边界处理方法，流场右上角粒子的位置及速度分布情况。

为了验证模拟结果，图 4 给出与 G.R.Liu［19］中有限差分结果对比图。由图4可知，垂向粒子点的水平速度和FDM的计算结果吻合较好，但是在水平中心线处的垂向速度分布上，δ-SPH方法与FDM计算结果存在偏差，均存在回流中心左移的现象。从计算效率和结果精度两方面考虑，镜像粒子点法完全能够满足粘性流场的需求。

为了研究GPU并行程序随粒子数量增加的加速效果及数值结果的收敛性，本文采用镜像粒子边界处理方法分别对流域内布置80×80个粒子点及100×100个粒子点2种计算模型进行了计算。图5(a)中给出6 400(80×80)个粒子点的最终流场分布。在靠近正方形顶部边界处可以看见明显的回流。图5(b)为不同粒子点使水平中心线处无量纲垂向速度分布。由图可知随着流场内实粒子数量的增加，水平中心线处的垂向速度基本相同。

图3 不同边界处理方法的最终流场分布Fig.3 Final flow pattern of different boundary processing

图4 腔内剪切流流场水平中心线处无量纲垂向速度分布及垂向中心线处无量纲水平速度Fig.4 Dimensionless vertical velocity of horizontal center line and dimensionless horizontal velocity of vertical center line in cavity shear flow

图5 6 400个粒子计算模型最终流场及不同粒子点计算模型水平中心线处无量纲垂向速度分布Fig.5 Eventually flow pattern of model with 6 400 particles and dimensionless horizontal velocity on vertical center line of different particle number module

4.2 Poiseuille 流动模拟

流体在两块无限长的固定平行板(y=0和y=l)之间的流动称之为Poiseuille流动。流域内流体在平行于x轴的外力F作用下在平板间逐渐流动并最终达到稳态。Morris等［20］给出了Poiseuille流动随时间(t＞0)变化的解析表达式:

动粘系数ν=10-6m2/s，传动力F=2×10-4m/s2，计算域l=10-3m，密度ρ=103kg/m3。通过解析式可知流场中的最大速度为2.5×10-5m/s，相应的雷诺数Re=2.5×10-2。流场计算域为 0.000 5 m×0.001 m，粒子点数量20×39，在上下边界处各布置20个粒子点，具体细节可参考文献［9］。计算选用五次样条核函数，时间步长 dt=0.000 1 s。表1 给出t=0.6 s时整个流场左侧第1列39个粒子的误差比较。表1的计算结果表明，δ-SPH方法在CPU上运算结果的误差范围大约是0.1%～0.5%。在 GPU的最大误差不超过1.5%。图6为在GPU和CPU平台上不同时刻Poiseuille流动水平方向速度和加速度分布情况。

表1 t=0.6 s GPU和CPU与Poiseuille流动的解析解速度结果比较Table 1 Velocity comparison of GPU and CPU with analytical solutions when t=0.6 s for Poiseuille flow

图6 不同时刻Poiseuille流动速度和加速度分布Fig.6 Velocity and acceleration of Poiseuille flow at different moments

4.3 Couette 流动模拟

Couette流动是t=0时刻，上层平板突然以一个平行于x轴的恒定速度v0运动。Morris等［20］给出其流场速度随时间变化的解析表达式为

计算域和 Poiseuille 流动，v0=2.5×10-5m/s，雷诺数为Re=2.5×10-2，采用五次样条核函数，时间步长dt=0.000 1 s。表 2 给出t=0.6 s时，采用 δ-SPH 方法在CPU和GPU上计算所得x方向计算速度与解析解的误差分布比较。图7为在GPU和CPU平台上不同时刻Couette流动的速度和加速度。通过采用δ-SPH方法在CPU和GPU上对低雷诺数的Poiseuille流动和Couette流动的模拟结果得到，在GPU上和CPU上计算结果没有太大差异，没有因GPU流处理器在表示浮点数方面能力较差而带来精度损失。

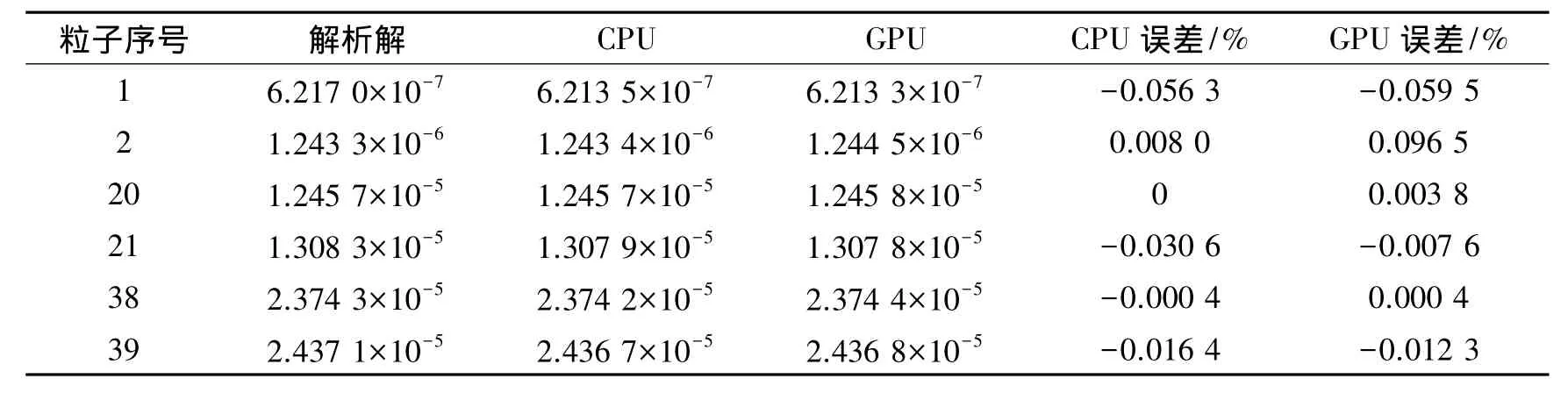
表2 t=0.6 s GPU和CPU与Coeutte流动的解析解速度结果比较Table 2 Velocity comparison of GPU and CPU with analytical solutions when t=0.6 s for Coeutte flow

图7 不同时刻Couette流动速度和加速度分布Fig.7 Velocity and acceleration distribution of Couette flow at different moments

4.4 孤立波砰击模拟

为了进一步验证本文方法的通用性，本节还给出孤立波砰击计算结果。其计算模型如图8所示。其中，水槽长10 m，水深0.25 m。在水槽末端壁面上距水池底部0.05 m及0.15 m处布置P0、P12个压力测点，在距离水槽左端2 m和8 m处分别布置浪高仪。粒子间距dx=0.01 m，粒子数为25 000(25×1 000)。其中，水槽末端粒子分布如图9所示。

模拟过程中造波板运动方程采用Ma［21］所给出的计算公式:

图8 孤立波砰击计算模型Fig.8 Calculating model of the solitary wave slamming

图9 2 m处孤立波波形Fig.9 Wave elevation of solitary wave at 2 m

图10 P0和P1点压力模拟结果与实验值Fig.10 Simulation pressure results and experimental pressure value at point P0and P1

从图9和图10可以看出，采用δ-SPH方法可以准确的模拟孤立波，数值模拟结果与实验值吻合十分完好。从P0与P1点的压力变化情况可以看出δ-SPH方法有效的减少了压力的非物理振荡，压力模拟结果与实验值误差较少，但是在孤立波与水槽末端直壁碰撞过后的压力模拟结果仍然与实际存在偏差。

4.5 GPU加速性能分析

与传统SPH方法相比，δ-SPH方法增加了密度修正项，需要求出修正后的密度梯度，其中涉及大量的矩阵运算，因此在计算时间上付出了一定的代价。本文中采用基于单个粒子和基于粒子对2种不同的并行设计方案实现了δ-SPH的GPU并行计算，所有的并行计算程序都是在NVIDIA的CUDA环境中开发，版本为5.5，模拟在一台PC机上运行，其配置如下:Intel Core(TM)i5-3470 CPU 3.20GHZ，4.0 GB内存和GTX660显卡，内存2G。

Couette流动和Poiseuille流动采用的是类似的计算模型，整个流场的流域实粒子、边界镜像粒子、周期性粒子共计1 222个粒子。采用镜像法进行边界处理的腔内剪切流动粒子数分别为:2 116、7 396、11 236个粒子。孤立波砰击模拟中整个流场的粒子总计28 168个粒子点。表3中的数据为各计算模型采用不同计算模式的单步时间消耗。

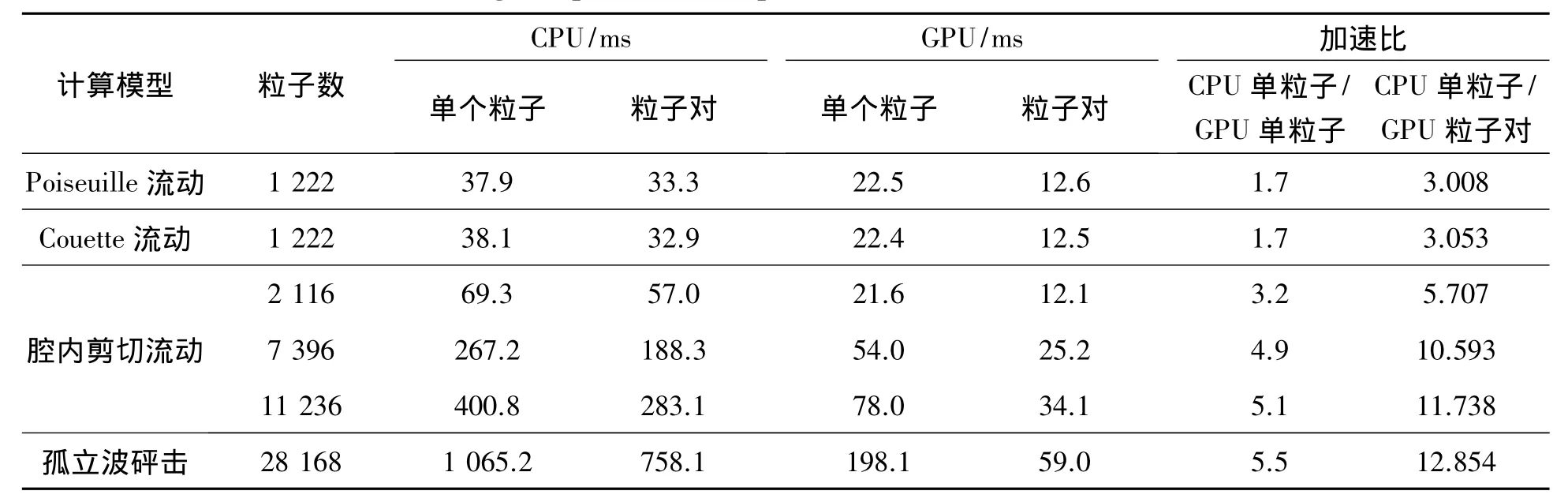
表3 不同计算模式的单步时间消耗Table 3 Single step time consumption with different calculation models

图11为各计算模型不同计算模式的时间消耗柱状图。从图中比较可得，不论是在CPU平台还是在GPU平台，采用粒子对进行计算总能得到很好的计算效率。随着粒子数的增加，GPU加速效果不断提高。采用粒子对并行模式的GPU计算方法明显优于传统的基于单个粒子的并行计算模式，虽然在计算的过程中大量的使用了原子操作，但随着粒子数量的增加，计算量的迅速增加有效的掩盖了原子操作所造成的时间等待。

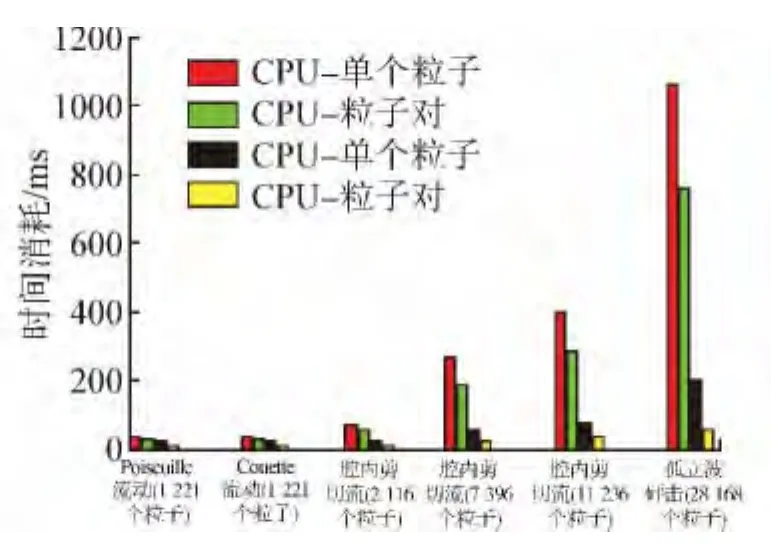
图11 不同计算模式的时间消耗柱状图Fig.11 Histograms of time consumption of different calculation

5 结论

本文对δ-SPH方法的GPU并行计算方法进行了研究，将其应用于对粘性流场问题的模拟。通过对相关数值模拟可以得到以下结论:

1)δ-SPH方法在模拟粘性流场问题时，采用传统的镜像粒子法对边界进行处理，由腔内剪切流的计算结果表明该方法的结果精度上较传统SPH有所提高。

2)在大规模计算时，采用基于粒子对模式的GPU并行计算方法比基于单个粒子的GPU并行计算方法的加速性能要好，其计算速度更是CPU串行计算不可比拟的。计算结果并不会因GPU流处理器在表示浮点数方面能力较差而带来精度损失。

3)随着粒子数量的增加，基于粒子对的GPU并行计算方法的加速效果增加迅速，体现了其在并行方面的强大优势。

［1］MONAGHAN J J.Simulating free surface flows with SPH［J］.Journal of Computational Physics，1994，110(2):399-406.

［2］COLAGROSSI A，LANDRINI M.Numerical simulation of interfacial flows by smoothed particle hydrodynamics［J］.Journal of Computational Physics，2003，191(2):448-475.

［3］COLAGROSSI A，LUGNI C，BROCCHINI M.A study of violent sloshing wave impacts using an improved SPH method［J］.Journal of Hydraulic Research，2010，48(S1):94-104.

［4］MONAGHAN J J.Particle methods for hydrodynamics［J］.Computer Physics Reports，1985，3(2):71-124.

［5］MARRONE S，ANTUONO M，COLAGROSSI A，et al.δ-SPH model for simulating violent impact flows［J］.Computer Methods in Applied Mechanics and Engineering，2011，200(13):1526-1542.

［6］MOLTENI D，COLAGROSSI A.A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH［J］.Computer Physics Communications，2009，180(6):861-872.

［7］高睿.SPH强非线性水动力学数值模型的改进与应用［D］.大连:大连理工大学，2011:20-78.GAO Rui.Correction and application of high nonlinear SPH hydrodynamic model［D］.Dalian:Dalian University of Technology，2011:20-78.

［8］郑兴，段文洋.K2_SPH方法及其对二维非线性水波的模拟［J］.计算物理，2011，28(5):659-666.ZHENG Xing，DUAN Wenyang.K2_SPH method and application for 2D nonlinear water wave simulation［J］.Chinese Journal of Computational Physics，2011，28(5):659-666.

［9］ZHENG Xing，DUAN Wenyang.Numerical simulation of dam breaking using smoothed particle hydrodynamics and viscosity behavior［J］.Journal of Marine Science and Application，2010，(9):34-41.

［10］XIONG Qingang，LI Bo，XU Ji.GPU-accelerated adaptive particle splitting and merging in SPH［J］.Computer Physics Communications，2013，184(7):1701-1707.

［11］徐锋.基于众核架构的并行 SPH算法的研究与实现［D］.上海:上海交通大学，2013:35-65.XU Feng.Research and implementation of the smoothed particle hydrodynamics algorithm based on multi-core architecture［D］.Shanghai:Shanghai Jiao Tong University，2013:35-65.

［12］朱小松.粒子法的并行加速及在液体晃荡研究中的应用［D］.大连:大连理工大学，2011:74-109.ZHU Xiaosong.Parallel acceleration of particle method and its application on the study of liquid sloshing［D］.Dalian:Dalian University of Technology，2011:74-109.

［13］郑兴.SPH方法改进研究及其在自由面流动问题中的应用［D］.哈尔滨:哈尔滨工程大学，2010:55-89.ZHENG Xing.An investigation of improved SPH and its application for free surface flow［D］.Harbin:Harbin Engineering University，2010:55-89.

［14］温婵娟，欧嘉蔚，贾金原.GPU通用计算平台上的SPH流体模拟［J］.计算机辅助设计与图形学学报，2010，22(3):406-411.WEN Chanjuan，OU Jiawei，JIA Jinyuan.GPU-based smoothed particle hydrodynamic fluid simulation［J］.Journal of Computer-Aided Design ＆ Computer Graphics，2010，22(3):406-411.

［15］RIFFERT H，HEROLD H，FLEBBE O，et al.Numerical aspects of the smoothed particle hydrodynamics method for simulating accretion disks［J］.Computer Physics Communications，1995，89(1-3):1-16.

［16］张舒，褚艳利.GPU高性能运算之CUDA［M］.北京:中国水利水电出版社，2009:34-56.

［17］LIU G R，LIU M B，LI Shaofan.Smoothed particle hydrodynamics—a meshfree method［J］.Computational Mechanics，2004，33(6):491.

［18］LIU M B，LIU G R，LAM K Y，et al.Smoothed particle hydrodynamics for numerical simulation of underwater explosion［J］.Computational Mechanics，2003，30(2):106-118.

［19］LIU M B，LIU G R，ZONG Z，et al.Numerical simulation of incompressible flows by SPH［C］//International Conference on Scientific and Engineering Computational.Beijing，China，2001:3-6.

［20］MORRIS J P，FOX P J，ZHU Yi.Modeling low Reynolds number incompressible flows using SPH［J］.Journal of Computational Physics，1997，136(1):214-226.

［21］MA Q W，ZHOU Juntao.MLPG-R method for numerical simulation of 2D breaking waves［J］.Computer Modeling in Engineering and Sciences，2009，43(3):277-304.