压水室隔舌安放角对离心泵无过载性能的影响

牟介刚，刘菲，谷云庆，郑水华，施瀚昱，王荣，汪洋，王成刚

(1.浙江工业大学机械工程学院，浙江杭州310014;2.浙江工业大学过程装备及其再制造教育部工程研究中心，浙江杭州310014;3.约瑟夫·傅里叶大学格勒诺布尔国立综合理工学院，格勒诺布尔38031)

作为耗能设备，离心泵过载导致设备毁坏一直是影响经济建设中成本控制的重要因素，而无过载的离心泵能在任意流量的工况点运行并避免泵过载，其实质是指泵的轴功率曲线有峰值或轴功率随流量的增加而有较小的变化，即轴功率曲线比较平坦，使泵的轴功率在关死扬程到零扬程(即从零流量到最大流量)范围内都小于或等于原动机的配套功率［1］。

20世纪30年代，Anderson［2］在研究离心泵的面积比理论时就指出，离心泵的最高效率是由叶轮和蜗壳共同决定的。而后，Worster［3］第一次从理论上证明了Anderson所提出的面积比原理的科学性。袁寿其等［4-6］总结了国内外学者对具有饱和轴功率特性的离心泵所作的相关研究，提出了离心泵的无过载理论，并推导了低比转数泵获得饱和轴功率特性的理论条件，提出了最大轴功率值及其流量值的估算公式。张金凤等［7］通过理论推导和正交试验研究，探讨了带分流叶片离心泵的无过载特性。王洋等［8-9］研究得出正确的堵塞流道方法可以降低离心泵的轴功率、提高离心泵的效率，以及有效地改善无过载离心泵的性能。施卫东等［10］通过数值模拟和理论分析证明采用正预旋能够较好地使低比转速离心泵实现无过载性能。杨军虎等［11］推导出仅与比转数、叶片出口角和叶片数相关的功率备用系数K，为无过载离心泵设计提供一种快捷的方法。研究人员也对无过载潜水排污泵的几何参数优化设计、试验研究、设计方法和数值模拟等方面进行了研究［12-13］。压水室作为离心泵主要的水力部件，也是离心泵无过载特性的主要影响因素。随着数值模拟技术以及三维建模技术的高速发展，对隔舌的研究也大量增加［14-15］。以上研究多侧重于从叶轮的角度展开对离心泵无过载性能的研究，而对于隔舌与离心泵无过载性能关系的研究相对较少。基于以上问题，以IH-100-65-200型化工离心泵为研究对象，建立具有不同隔舌安放角的离心泵计算模型，对该系列计算模型进行数值模拟，通过对比分析计算模型与原模型泵的性能及内部流场特征，研究压水室隔舌安放角对离心泵无过载性能的影响。

1 模型建立及参数设置

1.1 计算模型的建立

为了能够较好地研究离心泵隔舌安放角对泵性能的影响，以IH-100-65-200型化工离心泵为模型泵，比转速ns=94，设计工况点为Qopt=100 m3/h，Hopt=50 m，额定转速n=2 900 r/min，叶轮出口直径D2=215 mm，叶轮出口宽度b2=14 mm，叶轮进口直径D1=100 mm，隔舌安放角φ0=8°，压水室基圆直径D0=220 mm，压水室宽度b3=32 mm。根据模型泵的结构特点，并参照离心泵隔舌安放角的常用范围，取隔舌安放角 φ0分别为 4°、8°、12°、16°、20°的 5 个不同角度，流量Q为 20、40、60、80、100、120、140、160 m3/h 的8个工况点;分别对每一φ0下的计算模型在Q的8个工况点下进行数值模拟。隔舌安放角示意图如图1所示，为了使流体流动得到充分发展，需要保证进水管段和出水管段有足够的长度，故进水管道长度取400 mm，约为叶轮进口直径的4倍;出水管道长度取185 mm，约为蜗壳出口直径的3倍。

图1 隔舌安放角示意图Fig.1 Setting angle of volute tongue

1.2 网格划分及边界条件设置

因隔舌几何结构和隔舌区域流体流动状况较复杂，故需对隔舌区域进行分块加密网格处理;对于进/出水管段流体域采用Hex/Wedge单元的网格划分，网格类型选用Cooper;其他流体域采用Tet/Hybrid单元的网格划分，网格类型选用TGrid。在网格划分的过程中，为了保证EquiSize Skew与EquiAngle Skew均小于0.97，需检查所划分网格的质量，并不断对网格进行调试。离心泵流体域网格划分如图2所示。

图2 离心泵计算网格Fig.2 Computational mesh of centrifugal pump

输送介质为25℃清水，操作参考压力设为1×105Pa。定义入水管段入口面为速度入口，出水管段排出口面为自由出口;固壁处采用无滑移边界条件，在近壁处采用标准壁面函数。将全流道流体域类型定义为Fluid区域类型，并设置叶轮流体域运动形式为旋转［16-17］。选用多参考坐标系模型模拟离心泵内部流场，采用分离式解法对离心泵内部流场进行计算。在初始计算中各变量的离散格式采用一阶迎风格式，流场数值解法为Simple算法。为提高计算精度及加速收敛，在解收敛后将离散格式更改为二阶迎风格式，并将数值解法改为Simple算法的修正方法Simplec算法再进行计算，通过改变φ0来模拟离心泵在不同φ0下的内流特性，计算收敛精度为10-3，计算过程忽略重力的影响［18］。

1.3 数值计算方法

设离心泵内部流动为三维、定常不可压缩流动，在以恒角速度绕轴旋转的相对直角坐标系下，连续性方程、动量方程为［19］

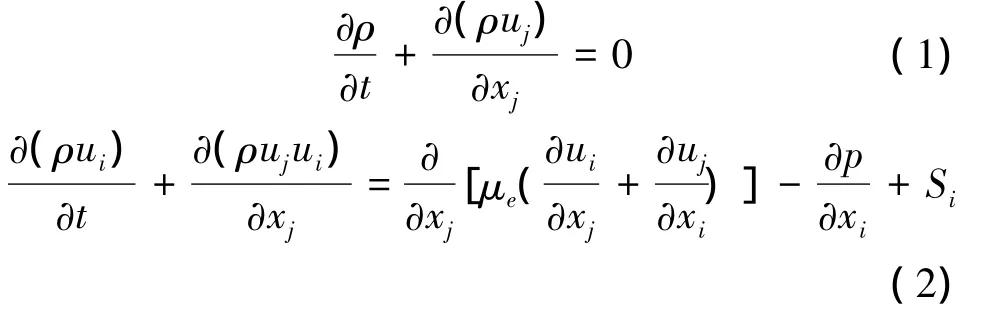
式中:ρ是流体密度，xi、xj分别代表各坐标分量，ui、uj代表平均相对速度分量，μe为有效粘性系数;p为压强，Si是广义源项。由于离心泵内部流动情况复杂，在非设计工况时，内部存在各种尺度的漩涡运动、回流以及二次流等复杂的湍流流动现象，所以选择可以更好地处理高应变率及流线弯曲程度较大的流动的RNGk-ε模型，湍动能k和湍流耗散率ε的约束公式如下［19］:

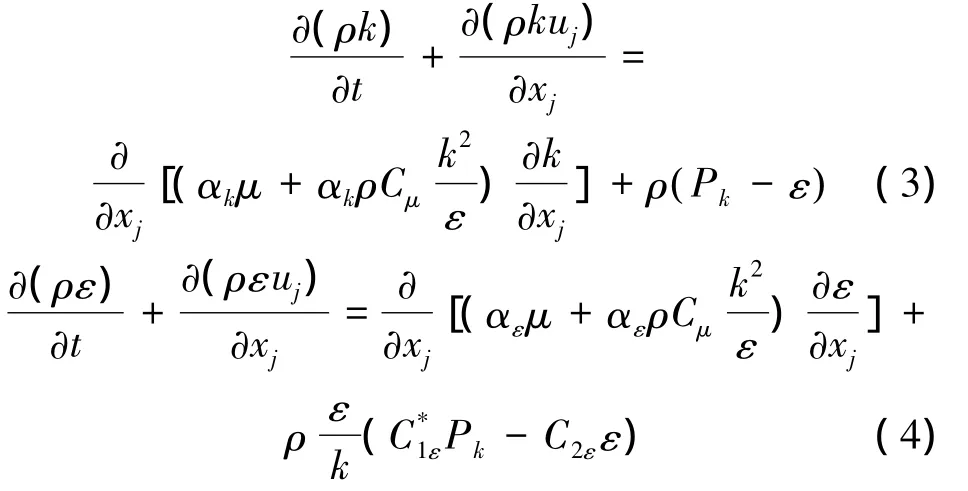
在式(3)右边项中增加的项为

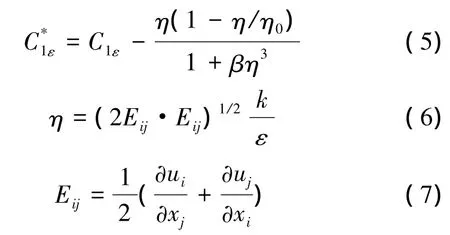
式中:μ是分子粘性系数，Pk代表湍动能生成项，Eij是时均应变率。常数的取值为:Cμ=0.084 5，αk= αε=1.39 ，C1ε=1.42，C2ε=1.68，η0=4.377，β =0.012 。

2 计算结果分析

2.1 隔舌安放角对离心泵轴功率的影响

对不同隔舌安放角下的流场进行数值模拟，分析不同流量工况下的轴功率值，得到如图3所示的不同隔舌安放角下离心泵轴功率曲线图。

图3 不同隔舌安放角下离心泵轴功率曲线Fig.3 Shaft power curves for different setting angles of volute tongue

由图3可知，在不同φ0下，离心泵轴功率曲线变化趋势基本一致，均在Q=120 m3/h时达到极值点。当φ0=4°时，小流量处轴功率增加且轴功率曲线变得更加陡峭。随着φ0逐渐增大，小流量处轴功率曲线趋势变得平缓。在大流量工况下，轴功率随着流量的增加而减小。通过比较不同φ0下的轴功率曲线可以看出，φ0越小，轴功率曲线在达到极值点后下降趋势越明显，而φ0较大时，如φ0为16°、20°时，轴功率曲线在达到极值点后下降趋势变得平缓，且极值点偏向大流量方向。在设计流量工况Qopt=100 m3/h 处，φ0为 4°、12°、16°、20°的轴功率值相对于φ0=8°的模型泵轴功率值的改变量分别为 0.34、-0.07、-0.37、-0.66 kW，可以看到喉部面积对轴功率的影响显著。模拟结果表明，φ0减小使压水室喉部面积增加，减小了叶轮叶片间出口面积与压水室喉部面积的面积比，因而更容易获得无过载轴功率特性。

2.2 隔舌安放角对离心泵扬程的影响

不同隔舌安放角下离心泵扬程随流量变化曲线图如图4所示。由图4可知，不同φ0的离心泵扬程曲线变化趋势基本一致，随着φ0的减小，喉部面积增大，扬程提高，且扬程曲线变得平坦易出现驼峰。这是因为当压水室喉部面积增加时，在同一流量下，流体流经压水室喉部的流速减小，从而减小了因叶轮出流速度不一致而产生的撞击损失和压水室内的沿程水力摩擦损失。而在大流量工况点处，φ0增大，这种撞击损失和沿程摩擦损失因速度的增加而在扬程曲线上体现得愈加明显，可以看到在大流量区，φ0为16°、20°的扬程曲线下降趋势更加陡峭。在设计流量工况Qopt=100 m3/h处，φ0为 4°、12°、16°、20°的扬程值相对于φ0=8°的模型泵扬程值的改变量分别为 0.48、-0.99、1.88、2.76 m，可以看到喉部面积对扬程的影响非常大。

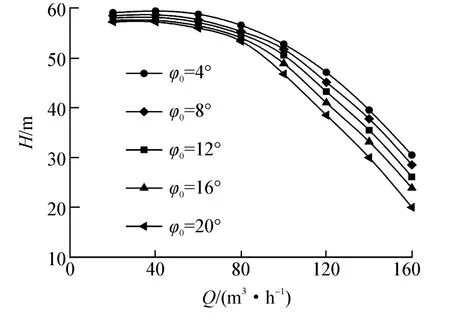
图4 不同隔舌安放角下离心泵扬程曲线Fig.4 Head curves for different setting angles of volute tongue

2.3 隔舌安放角对离心泵效率的影响

不同隔舌安放角下离心泵效率曲线如图5所示。由图5可知，不同φ0的离心泵效率曲线趋势基本一致，随着φ0的减小，喉部面积增大，效率曲线在小流量处变得陡峭，在大流量处趋势相对平缓，随着φ0的减小，效率提高且最高效率点向大流量方向移动。在设计流量工况Qopt=100 m3/h 处，φ0为 4°、12°、16°、20°的效率值相对于φ0=8°的模型泵效率曲线的改变量分别为 0.42%、-0.48%、-1.03%、-1.41%。可见，φ0逐渐增大，喉部面积减小，压水室喉部处的撞击损失和沿程摩擦损失逐渐增大。

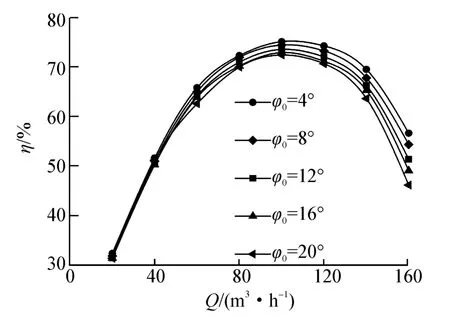
图5 不同隔舌安放角下离心泵效率曲线Fig.5 Efficiency curves for different setting angles of volute tongue

2.4 流场分析

以设计流量工况Qopt=100 m3/h时对不同隔舌安放角下泵内部流场进行分析。不同隔舌安放角下中心面静压云图如图6所示。由图6可知，在相同流量工况下，当φ0较大时，在隔舌附近，流经隔舌发生环流的部分流体静压分布梯度较大，且随着φ0的增大，流体在叶轮和蜗壳内的静压增加，在叶轮进口处静压减小。在第8断面到第9断面的流体域内，当φ0较小时，压水室喉部面积面积较大，流体扩散速度降低，在此处静压梯度较大，而当φ0较大时，第8断面到第9断面面积基本保持不变，流体在流经隔舌进入出水段前，静压变化已保持稳定。

不同隔舌安放角下中心面速度云图如图7所示，由图7可知，离心泵内部流场速度分布基本一致。流体流经叶轮进口到出口，速度逐渐增加;在进入蜗壳后，流道面积逐渐增大，速度有所减小。φ0的不同改变了流体流经第8断面进入蜗壳出水段的流道方向。在小流量工况下，当φ0=4°时，流体速度梯度方向与流道方向较一致，而当φ0增大时，流体流动方向和流道方向偏差逐渐增大，造成流体与蜗壳左侧壁面的撞击损失增加，而蜗壳右侧近壁面流体速度较小。在φ0为16°、20°时，流体与蜗壳壁面撞击损失较大，造成泵扬程和效率曲线在大流量处下降迅速。根据隔舌附近流体域的速度分布，φ0为4°、12°时较为理想。

图6 不同隔舌安放角下中心面静压云图Fig.6 Velocity distribution at the center of different setting angles of volute tongue

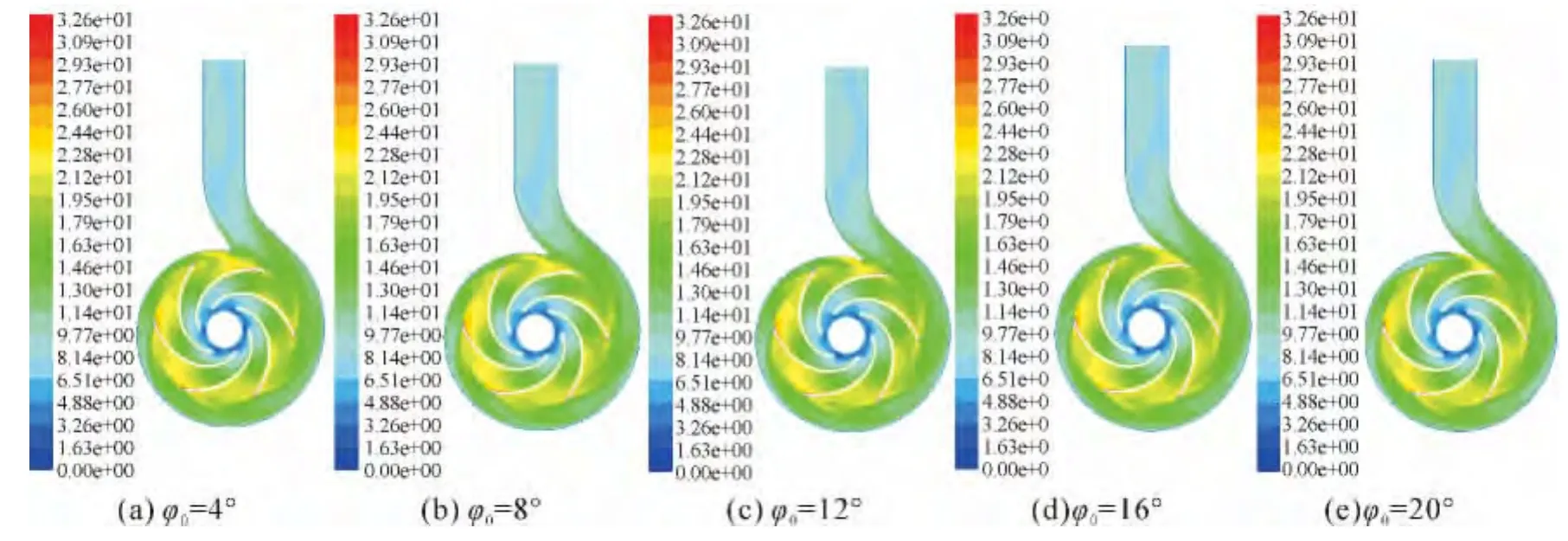
图7 不同隔舌安放角下中心面速度云图Fig.7 Pressure distribution at the center of setting angles of volute tongue

3 试验方法及结果分析

3.1 试验方法

为了准确了解压水室隔舌安放角对离心泵无过载性能的影响，验证数值模拟结果的可靠性并对其进行修正，因此需要进行试验研究。由于对隔舌安放角的改型方案较多，因此只选择φ0=16°进行试验。试验在新昌德力石化设备有限公司进行，以常温清水作为试验介质，测定泵在定转速、Q为 20、40、60、80、100、120、140、160 m3/h 的 8 个工况点的泵轴扭矩以及进出口压力，并计算不同工况点时泵轴功率、效率及扬程。由于对汽蚀测定精度要求不高，故采用开式试验台。试验装置如图8所示。

图8 试验现场Fig.8 Photography of test rig

3.2 试验结果分析

试验结果与数值模拟结果对比如图9所示。模拟扬程值、效率值、轴功率值与试验值相差分别为1.06～1.87 m、1.19%～3.5%、-0.18～-0.82 kW，除了在大流量工况点Q=160 m3/h处各测试值误差在8%左右，其余模拟误差均在5%之内。试验结果验证了在φ0增大后，泵扬程曲线变陡峭，最高效率点左移，轴功率曲线下降趋势变缓等数值模拟结果所预测的特性。扬程和效率的模拟值比试验值偏大，是因为在数值模拟过程中对流场进行了近似和简化，忽略了泵流道壁面粗糙度等影响因素，模拟结果较为真实，但仍无法完全反映流场的真实流动状况。

图9 试验性能与模拟性能对比图Fig.9 Comparison of test result and numerical simulation result

4 结论

1)压水室隔舌安放角是离心泵无过载性能的一个重要参数;减小φ0，压水室喉部面积增大，轴功率增加且轴功率曲线变得更加陡峭可以获得饱和轴功率性能来防止离心泵过载;增大φ0使得轴功率降低。

2)φ0减小，泵扬程提高，且扬程曲线变得平坦易出现驼峰;在设计流量工况下，φ0=4°的计算模型相较模型泵效率提高0.42%，且最高效率点向大流量方向移动;随着φ0增大，流体在叶轮和蜗壳内静压增加，在叶轮进口处静压减小;根据隔舌附近流体域的速度分布，φ0为4°、12°时较为理想。

3)模拟扬程值、效率值、轴功率值与试验值相差分别为1.06～1.87 m、1.19%～3.5%、-0.18～-0.82 kW，误差均在8%之内，表明数值模拟可以较准确的预测离心泵的H-Q及η-Q等外特性。

［1］施卫东，蒋婷，曹卫东，等.高扬程无过载潜水排污泵的优化设计与试验［J］.农业工程学报，2011，27(5):151-155.SHI Weidong，JIANG Ting，CAO Weidong，et al.Optimal design and experiment on a high-head non-overload submersible sewage pump［J］.Transactions of the CSAE，2011，27(5):151-155.

［2］ANDERSON H H.Mine pumps［J］.Journal of Mining Society，1984，10(6):34-38.

［3］WORSTER R C.The flow in voluts and its effects on centrifugal pump performance［J］.Proceedings of the Institution of Mechanical Engineers，1963，177(1):843-875.

［4］YUAN Shouqi，CAO Wuling，LI Shiying.Experimental investigation on non-overload centrifugal pumps［C］//Proceedings of 1992 International Conference on Pumps and System.Beijing，1992:389-397.

［5］YUAN Shouqi，CAO Wuling，LI Shiying et al.Theory and design method of non-overload centrifugal pumps［J］.Chinese Journal of Mechanical Engineering，1992，5(4):252-260.

［6］CARIDAD J，ASUAJE M，KENYERY F，et al.Characterization of a centrifugal pump impeller under two-phase flow conditions［J］.Journal of Petroleum Science and Engineering，2008，63(1-4):18-22.

［7］张金凤，沈艳宁，袁寿其，等.带分流叶片离心泵无过载特性的理论与试验研究［J］.排灌机械工程学报，2010，28(5):407-411，454.ZHANG Jinfeng，SHEN Yanning，YUAN Shouqi，et al.Theory and experiment on non-overload characteristics for centrifugal pump with splitters［J］.Journal of Drainage and Irrigation Machinery Engineering，2010，28(5):407-411，454.

［8］王洋，何文俊.基于Fluent的无过载离心泵改型设计［J］.农业机械学报，2009，40(9):85-88.WANG Yang，HE Wenjun.Improved attempt of non-overload centrifugal pumps based on Fluent［J］.Transactions of Chinese Society for Agricultural Machinery，2009，40(9):85-88.

［9］王洋，刘洁琼，何文俊.无过载离心泵结构参数优化设计［J］.农业工程学报，2012，28(3):33-37.WANG Yang，LIU Jieqiong，HE Wenjun.Parameter optimization of non-overload centrifugal pump［J］.Transactions of the CASE，2012，28(3):33-37.

［10］施卫东，李辉，陆伟刚，等.进口预旋对低比转速离心泵无过载性能的影响［J］.农业机械学报，2013，44(5):50-54，112.SHI Weidong，LI Hui，LU Weigang，et al.Effect of prewhirl flow on non-overload performance of low-specificspeed centrifugal pumps［J］.Transactions of Chinese Society for Agricultural Machinery，2013，44(5):50-54，112.

［11］杨军虎，郭斌，王玥，等.无过载离心泵设计参数与性能关系研究［J］.农业机械学报，2012，43(11):119-122，128.YANG Junhu，GUO Bin，WANG Yue，et al.Relationship of performances and design parameters for non-overload centrifugal pumps［J］.Transactions of Chinese Society for Agricultural Machinery，2012，43(11):119-122，128.

［12］曹卫东，李跃，张晓娣.低比转速污水泵叶片包角对水力性能的影响［J］.排灌机械，2009，27(6):363-366.CAO Weidong，LI Yue，ZHANG Xiaodi.Study on performance of low specific speed sewage pump with different vane wrap angles［J］.Drainage and Irrigation Machinery，2009，27(6):363-366.

［13］王凯，刘厚林，袁寿其，等.离心泵叶轮轴面图的3点水力优化［J］.哈尔滨工程大学学报，2012，33(7):834-838.WANG Kai，LIU Houlin，YUAN Shouqi，et al.Threepoint hydraulic optimization of impeller meridional plane for centrifugal pumps［J］.Journal of Harbin Engineering University，2012，33(7):834-838.

［14］刘宜，杨亚威，蔡玲春，等.隔舌安放角对离心泵性能影响的分析［J］.西华大学学报:自然科学版，2012，31(5):77-80.LIU Yi，YANG Yawei，CAI Lingchun，et al.Impact of placed angle of volute tongue on centrifugal pump performance［J］.Journal of Xihua University:Natural Science，2012，31(5):77-80.

［15］王秀勇，王灿星.叶片与蜗舌相对位置对离心泵性能数值模拟精度影响的研究［J］.力学季刊，2007，28(4):619-623.WANG Xiuyong，WANG Canxing.Effect of relative positions between blade and volute tongue on prediction of performance in simulation of centrifugal pump［J］.Chinese Quarterly of Mechanics，2007，28(4):619-623.

［16］MONTANTE G，LEE K C，BRUCATO A，et al.Numerical simulations of the dependency of flow pattern on impeller clearance in stirred vessels［J］.Chemical Engineering Science，2001，56(12):3751-3370.

［17］LI Yaojun，WANG Fujun.Numerical investigation of performance of an axial-flow pump with inducer［J］.Journal of Hydrodynamics，2007，19(6):705-711.

［18］GONZÁLEZ J，SANTOLARIA C.Unsteady flow structure and global variables in a centrifugal pump［J］.Journal of Fluids Engineering，2006，128(5):937-946.

［19］张淑佳，李贤华，朱保林，等.k-ε涡粘湍流模型用于离心泵数值模拟的适用性［J］.机械工程学报，2009，45(4):238-242.ZHANG Shujia，LI Xianhua，ZHU Baolin，et al.Applicability ofk-ε eddy viscosity turbulence models on numberical simulation of centrifugal pump［J］.Journal of Mechanical Engineering，2009，45(4):238-242.