基于控制单元的农村生活污水处理优化模型
2015-08-30王西琴中国人民大学农业与农村发展学院北京00872云南大学生态学与环境学院云南昆明65009中国环境科学研究院环境基准与风险评估国家重点实验室流域水生态保护技术研究室北京0002
王西琴,高 伟,张 远(.中国人民大学农业与农村发展学院,北京 00872;2.云南大学生态学与环境学院,云南 昆明 65009;中国环境科学研究院,环境基准与风险评估国家重点实验室,流域水生态保护技术研究室,北京0002)
基于控制单元的农村生活污水处理优化模型
王西琴1,高 伟2*,张 远3(1.中国人民大学农业与农村发展学院,北京 100872;2.云南大学生态学与环境学院,云南 昆明 650091;3中国环境科学研究院,环境基准与风险评估国家重点实验室,流域水生态保护技术研究室,北京100012)
基于系统动力学(SD)模拟模型和Powell优化模型,建立了农村生活污水污染物削减量与治理费用的SD-Powell模拟优化耦合模型,该模型可模拟预测污染物排放量,建立污染物削减量与治理费用函数关系.在此基础上,以污水治理费用最小为目标,以污水处理量为约束条件,对区域污染物削减量进行空间优化,得到最小治理费用下的最大污染物削减量.以常州市为例进行实证分析,模拟结果显示,2020年常州市农村生活污水COD和NH3-N排放量将达到16583t和2551t,分别比2008年增长4.60%和4.59%.采用聚类方法将常州市51个乡镇划分为4类控制单元,得到4类地区COD、NH3-N治理费用函数.各单位治理资金削减量存在明显差异,COD削减率的排序依次为:I类控制单元413kg/万元、IV类控制单元 380kg/万元、II类控制单元352kg/万元、III类控制单元348kg/万元,NH3-N削减率的排序依次为:III类控制单元65kg/万元、I类控制单元64kg/万元、IV类控制单元58kg/万元、II类控制单元54kg/万元,全区域削减率达到100%需要的治理费用约为16870万元.污染物削减空间优化结果显示,基于控制单元空间优化的削减效率高于平均分配的结果,治理费用在1000 -16870万元/a范围,COD、NH3-N的削减率分别提高6.4%和7.4%,4类地区的优先排序顺序依次为I类,IV类,II类和III类.
农村;生活污水;SD模型;费用函数;控制单元;太湖流域;常州市
农村生活污染具有分布广而分散、随机、开放式等特点[1].我国农村生活污水排放量约80~90亿t,且呈现不断增加的趋势[2],成为部分非点源污染的主要贡献源[3].随着农家乐、度假村、观光农业的兴起,大量旅游人群增加了农村生活污水排放量.据住房与建设部2005年《村庄人居环境现状与问题》的研究结果,96%的调查村庄(覆盖9个省43个县共74个村庄)没有污水处理系统,无序排放使农村地区的河、湖等水体受到普遍污染,同时,污水的下渗进一步引发流行性疾病的发生与传播,严重威胁农村饮用水安全.由于农村生活污水治理项目具有公共物品属性,且短期内不能产生经济效益,这就决定了其资金来源以政府为主导[4],资金问题也就成为制约农村生活污水治理的瓶颈.因此,如何用最少的资金获得最大的污染物削减量,是未来农村生活污水处理的关键.目前关于农村生活污水处理的研究,主要集中在污染物的核算[5-6]、污水处理技术以及处理模式分析[7-8]以及农村生活污水处理技术优选[9-10]等方面,缺乏对污染治理资金与削减量之间的定量研究,相关研究也仅从财务成本分析角度研究示范工程成本的有效性,如郝前进等[4]基于调研数据核算了上海和苏南地区主要农村污水示范工程的成本与效益,但重点是分析影响成本效益的因素,或者从宏观角度研究污水处理设施建设及营运的投资模式等[11].本文根据农村生活污水处理特点,建立污染物排放、治理费用的动态模拟与优化模型,研究不同处理模式污染物削减量与治理费用之间的函数关系,对污染物削减进行空间优化,从而实现相同治理费用下污染物削减量最大的目标.
1 模拟与优化方法
1.1建模思路
农村自然条件、经济发展水平的差异,决定了不同地区在同一时期可能选择不同的污水处理模式,单位处理量的污染治理资金的投入也存在着明显的差异.因此,分区、分类、有重点地对农村生活污染物进行调控,是现实所需,也是具有可操作性和实用性的方法.系统动力学通过系统内部变量之间的反馈,可模拟整个系统的动态变化,建立各子系统变量之间的复杂响应关系[12],本文选择系统动力学方法构建农村生活水污染模拟模型,建立污染物排放、削减量与治理费用之间的动态关系,建立不同处理模式下处理费用函数.本研究的治理费用包括投资费用和运行管理费用,以下统称治理费用.当前,我国农村生活污水处理模式主要有人工湿地处理技术、稳定塘处理技术、土地渗滤处理技术、接触氧化技术等[13].不同的生活污水处理技术,具有不同的处理效果,投资和运行费用也不同.在实际操作中,往往需要根据经济发展水平选择适合的处理技术.若将研究区作为一个大的污染控制单元,那么各分区污染物的削减量将决定整个地区的削减量.如果每个分区的污染物控制得到优化,就可以使总的污染物削减量达到最大,实现最小的治理费用和最大的污染物削减量目标.具体的思路如下:(1)划分控制单元.根据研究区人口密度、农民纯收入等指标对研究区进行划分,确定控制单元;(2)选择不同的处理模式.根据控制单元特点,选择生活污水处理技术,确定适合的处理模式及其治理费用;(3)模拟污染物排放量及其费用函数关系.依据人口、污水排放、污染物排放、污染物削减量、污染治理费用等相互之间的动态关系,构建农村生活污水、污染物排放、污染物治理费用SD模型,模拟污染物排放量,以及不同处理技术污染物削减量与治理费用之间函数关系;(4)污染物削减空间优化.基于不同地区不同处理技术和费用函数,建立空间优化模型,目标函数是整个区域污染物削减量最大,治理费用最小,采用优化模型得到各控制单元优先处理生活污水的排序,为整个区域污水处理优化提供定量化依据.
1.2农村生活污水污染物调控SD模型
1.2.1SD模型 根据农村生活污水的路径,将农村生活污染控制系统分为农村人口、经济发展、用水、排水、污水处理等5个模块,以农村人口数量为约束,建立人口数量、用水、排水、减污相关变量的函数关系,通过调节污水处理相关参数,同时考虑污水处理费用,建立系统流图.在总量控制目标一定的前提下,当污染物排放量增加时,减排压力就会增大,因此,需提高污水处理量减少污染物的排放,从而使排放量与设定的目标一致,形成负反馈回路.主要的反馈关系为:

本文主要模拟COD和NH3-N等2种污染物.以COD控制系统流图为例(图1),说明系统流图结构.限于篇幅,仅列出一种处理模式和一种污染物的流图.在区域人口总量和城镇化率的驱动下,农村人口数量发生变化,农村人口的变化带来2个效应:(1)农村人口变化导致农村生活用水量的变化,进而影响生活污水产生量和 COD、NH3-N产生量及其排放量;(2)农村人口变化影响农村总体收入水平,对污水治理模式及其费用产生影响.基于以上关系,在区域人口增长率、城镇化率和收入水平等因素的综合作用下,模拟农村生活污水、COD排放量和NH3-N排放量.污染物削减量的模拟主要取决于污水处理率和采用的处理技术,根据污水处理量及其变化可模拟出污水处理运行费用和设施建设投资费用,进而获得污水治理费用.污水处理量和污染物排放量通过减排压力连接起来,至此形成污染物排放与削减的负反馈回路.
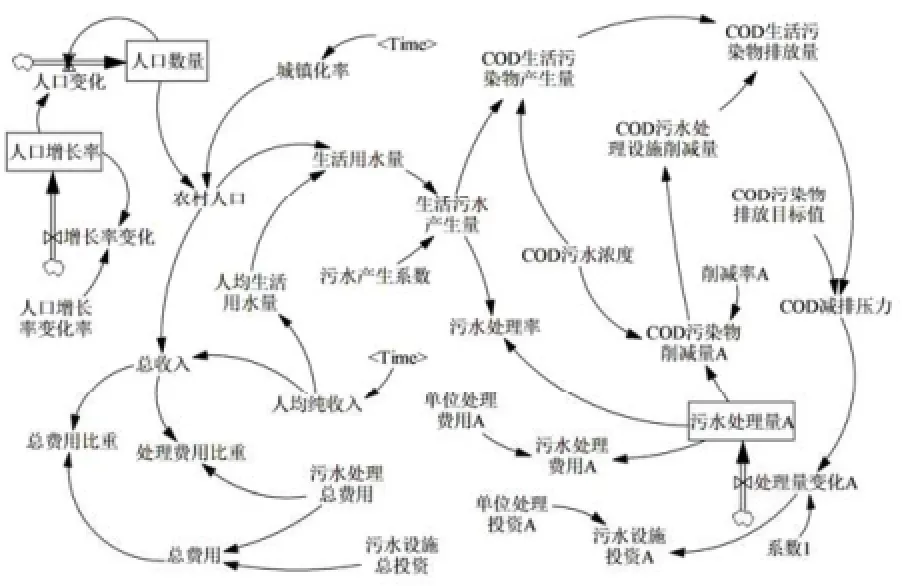
图1 农村生活污水污染物调控系统流图(COD)Fig.4 Chart of the rural domestic pollution control system (COD)
1.2.2模拟方程 农村生活污水污染物调控系统模拟了从污染物产生到排放的全过程,涉及的各个功能模块通过中间变量相互关联,构成一个具有驱动反馈功能系统模型.各个功能模块的主要模拟方程如下:
人口模拟方程:
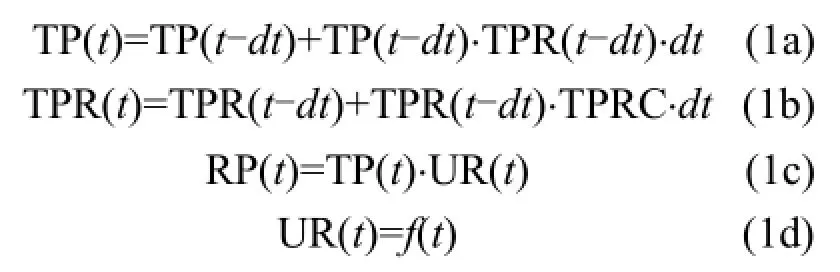
式中,t和dt分别是模拟的时间和时间步长;TP和RP分别为总人口数量(人)和农村人口数量(人);TPR为总人口数量从时间t-dt到dt的增长速度;TPRC为总人口增长速度从时间t-dt到dt的变化率;UR为城镇化率,在该模型中设置为表函数,随时间变化取不同数值.
用排水模拟方程:
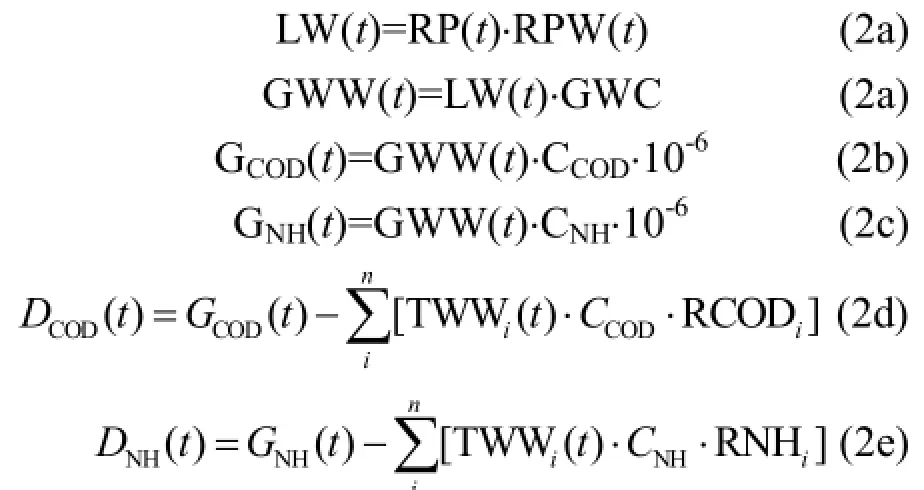
式中,LW为农村生活用水量(t);RPW为农村人均生活用水量(t/人);GWW为农村生活污水产生量(t);GWC为农村生活污水产生系数,根据常州市现状年的生活用水与排水比例,取值 0.825;GCOD为农村生活污水COD产生量(t);CCOD为生活污水COD浓度(mg/L),根据现状年城镇生活污水取325mg/L;GNH为农村生活污水 NH3-N产生量(t);CNH为生活污水NH3-N浓度(mg/L),根据现状年城镇生活污水统计数据取 50mg/L;DCOD和DNH分别为农村生活污水的COD和NH3-N排放量(t);i为污水处理工艺;TWW 为污水处理量(t);RCOD和RNH分别指污水处理工艺COD和NH3-N的削减率.
收入与费用模拟方程:
早产儿即胎龄未满37周的活产婴儿,又被称为未成熟儿。早产儿出生体质量多不足2 500 g,各器官及系统功能适应能力差,皮肤组织薄嫩,皮下肌肉、脂肪少,体温调节、代谢功能、凝血功能、脏腑功能较差,且自母体获得的免疫因子及抗体量少,抵抗力弱,极易发生感染,且感染发生后的治疗效果较足月儿差[9-10]。因此,临床需加强对胎膜早破早产儿宫内感染的早期诊断,以利于尽早接受有效的对症治疗,改善疾病预后。
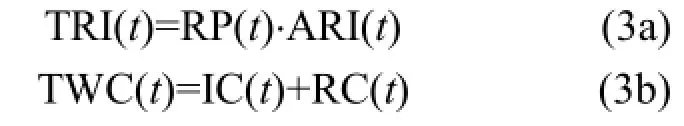
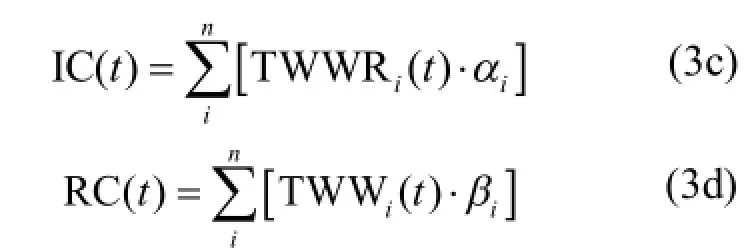
式中,TRI和ARI分别为农民总收入(元)和农民人均收入(元);TWC为农村生活污水治理总费用(元);IC和 RC分别是污水治理设施投资与运行费用(元);TWWR分别表示新增污水处理量(t);α 和β分别指单位污水治理投资费用和处理费用(元/t).
1.3污染物削减空间优化模型
目前系统动力学模型的优化主要有情景分析法[14]和SD-MOP(系统动力学-多目标优化)耦合法[15-16],其中,情景分析法的不足是情景数量有限,无法穷举所有可能的情况,因此,这种方法只能提供非劣解;SD-MOP法则是根据系统动力学的模拟结果,选择几个典型年的模拟值作为优化模型的参数,但模拟与优化不能实现直接耦合,故优化对模拟的信息利用不够完全.本文在系统动力学模拟模型的基础上,基于 Vensim® DSS (Ventana Simulation Environment Decision Support System)系统自带的Powell寻优工具,建立SD-Powell模拟优化耦合模型,从而实现最小污染治理资金与最大污染物削减量的空间分配.该方法具有二次收敛性质,特点是不需要写出优化模型的解析表达式,只需界定优化目标和优化变量的取值范围,同时具有较高的优化效率,可进行复杂的多维函数曲面寻优,是解决复杂系统问题常用的优化方法[17].
优化目标是农村生活污水治理总费用最小,具体模型如下:
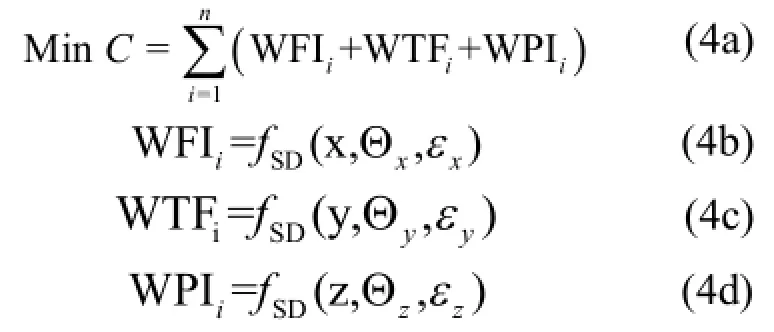
式中:C代表研究区农村生活污水治理总费用(万元);WFI为农村生活污水处理设施投资费用(万元);WTF表示污水处理设施运行费用(万元);WPI是农村生活污水管网建设投资费用(万元);i代表污染控制分区,i=1, 2, …, n,n为分区或者控制单元数量;x,y, z表示SD模型中与WFI、WTF和WPI相关的变量;Θ为SD模型变量集,ε 为SD模型误差项,fSD为SD模型中的不同变量数值响应关系,为多个方程的组合.
约束条件是控制单元农村生活污水处理量范围,表达式如下:
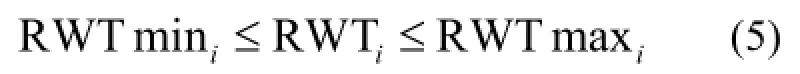
式中:RWT为农村生活污水年处理量(万 t);RWTmin表示农村生活污水年处理量下限(万t);RWTmax表示农村生活污水年处理量上限(万t).上述优化模型采用Vensim® DSS软件的鲍威尔爬山算法(Powell hill climbing algorithm)求解.
2 实例研究
2.1研究区概况
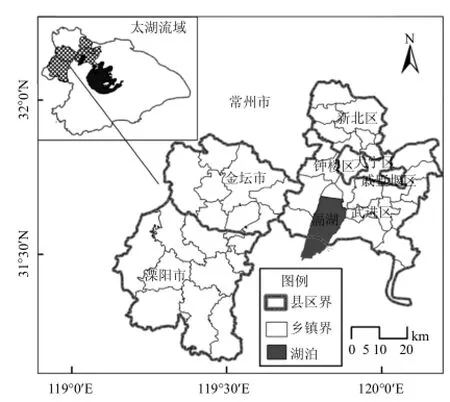
图2 常州市地理位置与行政区划Fig. 2 Geographic location and districts of Changzhou city
2.2控制单元划分
目前,常州市采用的污水处理方式约有24种,其中微动力净化装置-人工湿地、塔式蚯蚓生态滤池-生态沟渠和缓流纳污河浜原位增氧-动态生态等3种处理方式应用较多,占60%以上.常州市各乡镇(街道)人口密度、产业结构和收入水平存在差异显著,农民纯收入最高武进区奔牛镇14601元/人,最低的新北区西夏墅镇8700元/人,奔牛镇第一产比例和人口密度分别是西夏墅镇的0.05和2.22倍.本文选取人口密度(PD)、农村人均纯收入(RI)等2项指标作为控制单元划分的依据,两者 Pearson相关性为 0.483,相关性较低.采用层次聚类法,在SPSS 18.0软件中对常州市51个乡镇(街道)进行聚类,可划分为4种类型的控制单元(图3、表1),第I类控制单元包括6个乡镇,特点是人口密度最高,第一产业比重最小,人均收入水平相对较高,主要分布在常州市城区,包括:湖塘镇、雕庄街道、红梅街道、五星街道、永红街道、茶山街道等;第II类控制单元有7个乡镇,人口密度相对较高,而农村人均收入水平最高,分别为;牛塘镇、横林镇、青龙街道、新闸镇、西林街道、丁堰镇、溧城镇等;第III类控制单元,包括20个乡镇,人口密度和农民收入水平均处于较低水平,包括:洛阳镇、遥观镇、横山桥镇、郑陆镇、礼嘉镇、邹区镇、湟里镇、奔牛镇、龙虎塘街道、春江镇、新桥镇、薛家镇、罗溪镇、西夏墅镇、孟河镇、三井街道、北港街道、潞城镇、金城镇、开发区等.第IV类地区,包括18个乡镇,人口密度最低,农民收入水平也最低,主要分布在远离城区的地区,包括雪堰镇、前黄镇、嘉泽镇、埭头镇、上黄镇、戴埠镇、天目湖镇、别桥镇、上兴镇、竹箦镇、南渡镇、社渚镇、直溪镇、朱林镇、薛埠镇、指前镇、儒林镇、尧塘镇等.
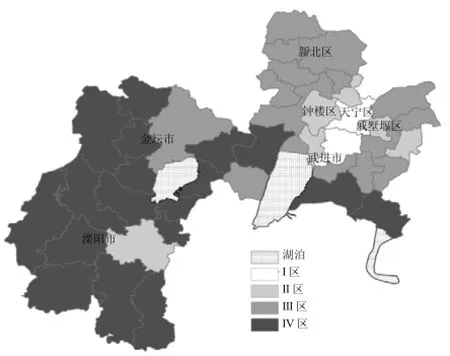
图3 常州市51个乡镇控制单元划分结果Fig.4 Control unit of the 51 villages in Changzhou City
依据江苏省建设厅颁布的《农村生活污水处理适用技术指南》[18],可根据人口密度和人均收入 2项指标作为农村生活污水处理模式的选择依据,为此,可以确定4个控制单元的适用处理技术,可供常州市选用的有4种污水处理技术,分别是C、B、A、D4种处理模式(表2).这4种处理模式对应着不同的户均建设成本和运行费用,依次作为污水治理费用模拟优化的依据(表1).
2.3模拟与优化结果
2.3.1污染物排放量模拟结果 本文数据来源于常州市城市发展总体规划(2004~2020年),常州市水资源公报,常州市统计年鉴等.为了使不同年份的经济数据具有可比性,农民人均纯收入数据均换算为2005年可比价.模型起始年份2008 年,终止年份为2020年,计算时间步长1年.
基于农村生活污水污染物 SD模拟模型,2008年常州市的COD和NH3-N排放量分别为15853和2439t,4个控制单元的排放量表现出显著差异(表3).第III控制单元由于农村人口密度大,污染物排放量最高,占常州市的 38%;其次是第IV控制单元,占31%;第I控制单元位于市区,农村人口数量占比例最低,生活污染物排放量仅占14%.

表1 常州市各控制单元农村生活污水处理适用模式Table 1 The pollution treatment mode for rural sewage treatment in different control units in Changzhou City

表2 江苏省农村生活污水处理技术的适用范围、处理效果与费用Table 1 The applicability, treatment performance and cost for rural sewage treatment techniques in Jiangsu province
根据SD模型得到2020年常州市人口总量将达到486万人,城镇化率达到75%.由于城镇化速度高于人口增长速度,农村人口数量总体表现为下降趋势,由2008年的172万人下降到2020年的 122万人,然而,随着农村生活水平的提高,人均农村生活用水定额有增加的趋势,将由2008 年94L/d上升至2020年的139L/d, 2020年常州市农村生活污水COD和NH3-N排放量将达到16583,2551t,分别比2008年增长4.60%和4.59%(表3).
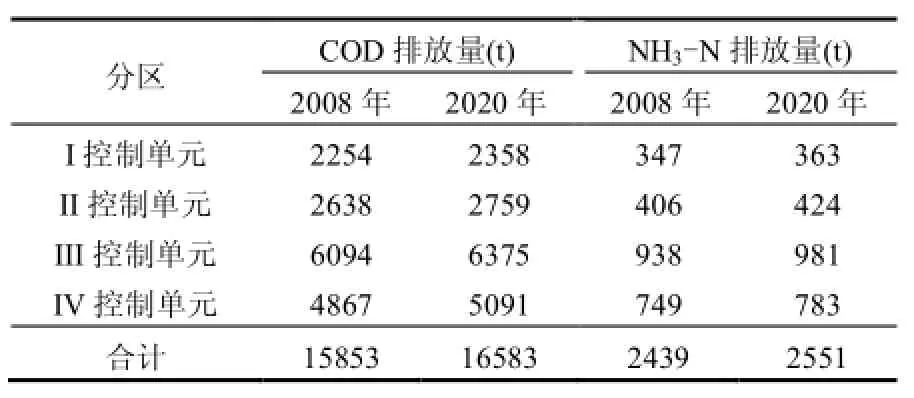
表3 常州市农村生活污染物排放量模拟结果(2020年)Table 1 Simulated emission of COD and Ammonia in different control units in Changzhou City (2020年)
2.2.2各控制单元污染物削减量与治理费用函数关系 依据优化模型,可得到4个控制单元污染物削减量与治理费用的函数关系(表4)从COD费用函数看,I类控制单元单位资金的削减量最大,平均每万元削减COD 413kg,其他依次是 IV类控制单元 380kg/万元、II类控制单元 352kg/万元、III类控制单元348kg/万元.NH3-N单位资金削减量排序依次为: III类控制单元 65kg/万元,I类控制单元64kg/万元、IV类控制单元58kg/万元和II类控制单元54kg/万元.2种污染物单位资金削减量在各分区存在差异,主要原因是不同处理技术对这2种污染物的削减效果不同,例如A污水处理模式对COD的削减率(进出水浓度差与进水浓度比例)比NH3-N的低15%,B污水处理模式的COD削减率比NH3-N高10%.在实际中可根据研究区 COD、NH3-N排放量的特点,优先选择某种指标作为治理资金排序依据,本文选择COD为排序依据.
治理费用函数在各个分区内存在一定的适用范围,即当污水处理率达到100%时,即使增加治理费用,也不会提高污染物削减能力.根据各控制单元的污染物削减潜力与费用效益关系,可以得到在 100%生活污水处理率的情况下 4个分区需要的治理费用,分别为2567,2937,6407, 4959万元/年,对应的COD削减量分别为1061, 1035,2230,1883t/a;NH3-N 削减量分别为 163, 159,417,290t/a.
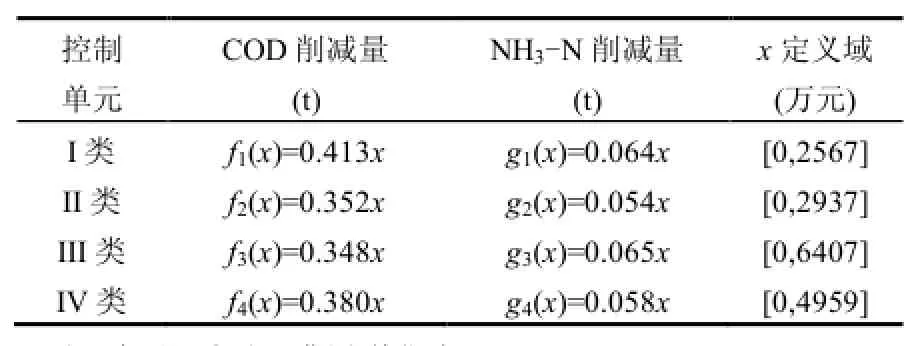
表4 常州市各控制单元农村生活污水处理费用与削减量函数Table 1 Treatment cost and pollution reduction function for rural sewage treatment in different control units in Changzhou City
2.2.3常州市污染物削减量及其治理费用优化结果 各控制单元治理费用与污染物削减量关系存在差异,为污染物控制空间优化提供了可能.在总的治理费用一定的情况下,若想达到全区域污染物削减的最大化,应将资金优先投入到单位资金削减量大的控制单元,当该控制单元的削减潜力达到最大,再依次向其他控制单元投资,由此可得到同样的污染治理资金下最大的污染物削减率.根据4个分区的污染物削减量与治理费用的关系,以削减效率最高(即单位治理资金的污染物削减量最大)为原则,可以得到常州市农村生活污水费用函数.由于COD和NH3-N的削减效率排序在各个分区存在差异(表 4),例如 COD削减效率最高的是I区,而NH3-N的削减效率最高的是III区,但在污水处理过程中,这2种污染物又是同时被削减的,鉴于 COD削减效率是NH3-N的5倍以上,平均每增加1万元的投入可新增COD削减量368kg,NH3-N削减量61kg.以COD指标为各分区费用效益函数的排序指标(公式6).由此看出,当治理资金达到16870万元/年时,常州市2020年农村生活污染物削减率达到100%.此时,污染物削减能力 COD 6208t /a和NH3-N 1029t/a.治理费用范围介于0~16870万元/a.对应着不同的治理费用范围,单位治理费用的污染物削减量表现出明显的差异.可分为4个范围:(1)治理资金介于 0~2567万元/a,最大的削减效率为COD 413kg/万元、NH3-N 64kg /万元;(2)治理资金介于2567~7526万元/年,最大的削减效率为COD 380kg/万元、NH3-N 58kg/万元;(3)治理资金为7526~10463万元/a,最大的削减效率为COD 352kg/万元、NH3-N 54kg/万元;(4)治理资金介于 10463~16870万元/a,最大的削减效率为COD 348kg/万元、NH3-N 65kg/万元.

式中,f(x)和g(x)分别为常州市农村生活COD和NH3-N削减总量(t/a);x为污水治理投入总费用(万元/a).
2.3优化结果与非优化削减量对比
如果不考虑控制单元之间处理效果的差异,即削减率的优先排序,那么在同样的治理费用下,按照平均分配的原则将治理资金分配到 4个控制单元,则得到不同的治理费用函数关系(图 4).由图4看出,平均分配得到的单位资金污染物削减量远低于优化结果.可以分为以下3种情景:
(1)治理费用低于1000万元/a,优化与非优化污染物削减效率差异较小,COD削减量差距92~134t/a,NH3-N削减量差距168t/a.
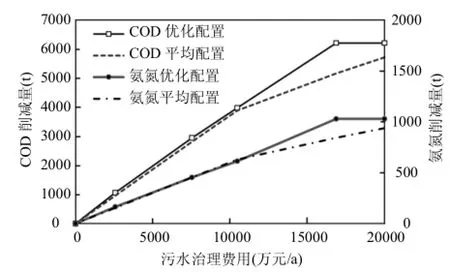
图4 治理费用优化配置与平均配置污染物削减量比较Fig.4 Pollutant reduction amount comparison of optimization and average allocation
(2)治理费用介于 1000 ~16870万元/a,优化与非优化结果差距最大,COD削减量差距1044t/a,NH3-N削减量差距186t/a.其原因是有些控制单元治理资金过剩,削减效率降低.
(3)治理费用高于16870万元,优化与非优化的削减能力差异出现减少趋势,优化与非优化COD削减量差距490t/a,NH3-N削减量差距91t/a.其原因是各控制单元削减潜力逐渐降低.
3 结论
3.1采用系统动力学(SD)模型,构建了农村生活污染物产生-削减-排放-治理费用的模拟与优化耦合模型.该模型具有模拟污染物排放量与优化治理费用的功能,可得到不同控制单元的处理费用函数以及区域的费用函数,进而获得不同控制单元优先削减的排序.该模型能够模拟出不同治理费用下各控制单元的最优削减量,即如何将有限的污染治理资金分配到各个控制分区,以实现最大的污染物削减量.实例研究结果表明,采用该模型具有一定的合理性和可操作性.为模拟预测农村生活污染物量,以及污染物治理费用函数提供了指导.
3.2将常州市51个乡镇划分为4类控制单元,得到了4个单元的治理费用函数,常州市2020年农村生活污染物削减率达到 100%.治理费用约16870万元/年,在相同的治理费用下,空间优化分配治理资金的处理效率大于平均分配的处理效率,治理费用介于1000万元/年—16870万元/年,优化与非优化结果差距最大,COD削减量差距1044t/年,NH3-N削减量差距 186t/年.因此,应将资金优先投入到单位资金削减量大的控制单元,可实现最小的治理费用和最大的削减率,常州市的优先排序依次为:I类控制单元、IV类控制单元、II类控制单元、III类控制单元.
[1] 袁晓燕,余志敏,施卫明.浙北地区平原河网农村小流域面源污染调查与防治对策——以德清县武康镇新琪村为例 [J]. 生态与农村环境学报, 2010,26,(3):193-198.
[2] 孙兴旺,马友华,王桂苓,等.中国重点流域农村生活污水处理现状及其技术研究 [J]. 中国农学通报, 2010,26,(18):384-388.
[3] 邱 斌,李萍萍,钟晨宇,等.海河流域农村非点源污染现状及空间特征分析 [J]. 中国环境科学, 2012,32(3):564-570.
[4] 郝前进,张 苹.农村生活污水治理示范工程的成本有效性研究——以上海和苏南地区为例 [J]. 2010,20(1):108-111.
[5] 王文林,胡孟春,唐晓燕.太湖流域农村生活污水产排污系数测算 [J]. 生态与农村环境学报, 2010,26(6):616-621.
[6] 李 卉,苏保林,张 倩,等.平原河网地区农村生活污染入河机制 [J]. 生态与农村环境学报, 2011,27(4):110-112.
[7] 梁 祝,倪晋仁.农村生活污水处理技术与政策选择 [J]. 中国地质大学学报(社会科学版), 2007,73):18-22.
[8] 马鲁铭,王云龙,刘志刚,等.南方农村生活污水处理目标及工艺模式探讨 [J]. 中国环境科学, 2013,33(1):118-122.
[9] 夏训峰,王明新,闵 慧,等.基于模糊优劣系数法的农村生活污水处理技术优选评价方法 [J]. 环境科学学报, 2012,32(9):2287-2293.
[10] 张英民,卢文洲,王 炜,等.农村生活污水处理工程技术方案优选研究 [J]. 中国环境科学, 2013,33(S1):210-214.
[11] 姜 海,杨杉杉,冯淑怡,等.基于广义收益—成本分析的农村面源污染治理策略 [J]. 中国环境科学, 2013,33(4):762-767.
[12] 钟永光,贾晓菁,李 旭.系统动力学 [M]. 北京:科学出版社, 2009.
[13] 李怀正.农村生活污水处理实用技术改进措施 [J]. 中国水利, 2010,(3):67.
[14] 赵 妍,田 强,尚金城.城市生态工业系统模拟、优化调控方法研究 [J]. 生态环境学报, 2010,19(6):1416-1421.
[15] 周 丰,郭怀成.不确定性非线性系统"模拟-优化"耦合模型研究 [M]. 北京:科学出版社, 2010.
[16] 张雪花,张宏伟,张宝安.SD-MOP整合模型在区域发展战略规划研究中的应用 [J]. 系统工程, 2007,25(9):65-72.
[17] 王鹏涛. Powell寻优法及其应用 [J]. 系统工程理论与实践, 1997,(9):64-66.
[18] 江苏省住房和城乡建设厅.农村生活污水处理适用技术指南[EB/OL].http://www.jscin.gov.cn/web/showinfo/showinfo.aspx?i nfoid=c973e588-d563-468b-8968-aa98dd7d3ad5/2015-03-07.
Optimization of rural domestic sewage treatment models.
WANG Xi-qin1, GAO Wei2*, ZHANG Yuan3(1.School of Agricultural Economics and Rural Development, Renmin University of China, Beijing 100872, China;2.School of Ecology and Environmental Science, Yunnan University, Kunming 650091, China;3.State Key Laboratory of Environmental Criteria and Risk Assessment, Laboratory of Riverine Ecological Conservation and Technology, Chinese Research Academy of Environmental Sciences, Beijing 100012, China).
China Environmental Science, 2015,35(9):2835~2842
Rural sewage treatment is an important task of the New Rural Construction in China, which also plays a key role in improving the rural ecological environment. In this study, using system dynamic (SD) model and Powell optimization model, a SD-Powell coupled model with simulation and optimization function was set up to simulate and predict the amount of pollutant discharge, and to establish the functional relationship of pollutant reduction and cost. Taking Changzhou City in Jiangsu Province as a case study, the calculated results indicate that COD and ammonia emissions will reach up to 16583 t and 2551 t in 2020 respectively, increased by 4.60% and 4.59% compared to 2008. The 51 towns in Changzhou City were divided into four categories of control units using clustering method. The treatment cost functions for COD and ammonia in different control units were obtained, with the treatment cost in four units varying from 348 kg to 413 kg per ten thousand Yuan RMB for COD, and 54 kg to 65 kg per ten thousand Yuan RMB for ammonia. The total cost will be 168.7 million RMB Yuan if the pollutant reduction rate in the whole area reaches 100%. The results show that the pollutant reduction rate by cost optimization was better than the cost average allocation. Compared to average allocation results, the method used in this study could increase reduction effectiveness of the two pollutants COD and ammonia by 6.4% and 7.4%, respectively. The optimal treatment cost was between 10and 168.7 million RMB per year under different reduction rates and the treatment cost for priority unit was in the order of I>IV>II >III.
rural areas;rural sewage;system dynamics model;cost function;control unit;Taihu Basin;Changzhou City
X506
A
1000-6923(2015)09-2835-08
2015-02-06
国家水体污染控制与治理科技重大专项(2012ZX07501-001); 中国科学院开放基金(KF311201303081)
*责任作者, 讲师, gaoweird@163.com
王西琴(1965-),女,陕西西安人,教授,博士,主要从事资源经济与环境管理.发表论文80余篇.
