做好课前设计是高效课堂的保证

周玉喜

【教学目标】

1. 知识与技能：掌握三角形内角和定理及其推理过程，能应用三角形内角和定理解决一些简单的实际问题.

2. 过程与方法：经历实验活动的过程，得出三角形的内角和定理；能用平行线的性质推出这一定理并初步学会利用辅助线证题；培养学生观察、实验和进行简单逻辑推理的能力.

3. 情感态度与价值观：通过对定理及推论的分析与讨论，发展学生的求同和求异的思维能力，培养学生联系与转化的辩证思想.

【重点与难点】

1. 重点： 三角形内角和定理的理解与运用；

2. 难点： 三角形内角和定理的证明.

【课前准备】

每个学生准备好两个由硬纸片剪出的三角形、三角尺、量角器.

【教学策略】

自主合作探究的教学模式.

【教学流程设计】

一、创设情景，优化导入

【问题1】平角的度数为多少度？两直线平行，同旁内角的和为多少度？

学生很容易回答出正确的结论.为新知进一步探究打下坚实的基础.

【问题2】在△ABC中，∠A+∠B+∠C等于多少度？如何得到这一结论呢？

生：三角形的内角和为180°.用量角器测量.小学学习过.

师：小学学习时，老师给出初步结论，具体为什么三角形的内角和为180°还不十分了解.由于测量存在误差，我们须要用更准确、更严谨的方法来验证，用数学方法进行证明，今天，我们就来探讨一下如何验证和证明这一结论.

【设计意图】新课引入的好坏在某种程度上关系到课堂教学的成败，本节课从旧知识切入，特别是从知识体系考虑引入，使学生感觉本节课学习的内容自然合理.把问题作为教学的出发点，创设问题情境，激发学生学习兴趣和求知欲.同时让学生体会从特殊到一般的思考问题方法.

二、积极探究，发现规律

活动一：

【问题1】用量角器自主测量准备好的三角形内角的和是多少度？

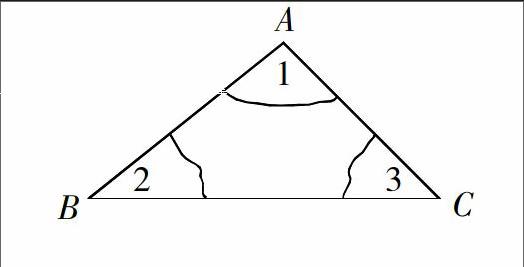
【问题2】在纸片上画任意的三角形△ABC，把三个角分别涂色，动手操作剪下内角拼一拼，你能得到什么结论？

学生活动1：

生：自主用量角器测量，得到三个内角之和的大小.有的大于180°，有的小于180°，有的等于180°.

师：实验测量存在误差，下面进行另一个活动.

学生活动2：

师：在所准备的三角形硬纸片上标出三个内角的编码，动手把三角形的两个角剪下进行拼接，能否得到一个平角或者同旁内角.

生：能.学生开始操作.

师：（动画演示）下图是得到180°的思路进行的拼接方法展示图.

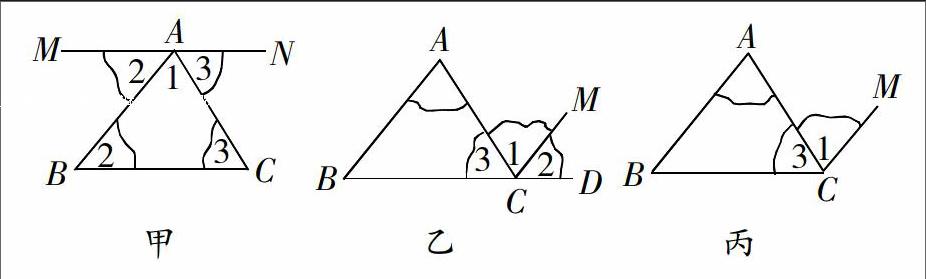
【问题3】如图甲，直线MN与直线BC有怎样的关系？它是图形中原来就存在的一条直线吗？

直线MN∥BC，它是我们自己添加上去的.

在证明的过程中，须要说明如何添加这一辅助线.

板书探究结论：三角形的三个角之和为180°.

【问题4】由刚才的剪拼办法，可以想出怎样的证明方法来说明上面结论的正确性呢？

强调：辅助线的添加.证明思路为将三角形的三个角为180°转化为一个平角或同旁内角互补，利用平行线的性质进行证明.

【问题5】结合图乙、图丙，你能得到怎样的证明方法？还有其他的证明方法吗？简单说明同旁内角互补这一思路的证明过程.

【设计意图】通过引导学生写出题目的条件和结论，提高学生的逻辑思维能力，同时培养学生严谨的科学态度.要让学生知道“辅助线”是以后解决几何问题的工具.它的作用在于充分利用条件；恰当转化条件；恰当转化结论；充分提示题目中各元素间的一些不明显的关系，达到化难为易解决问题的目的.

三、例题解析，深化应用

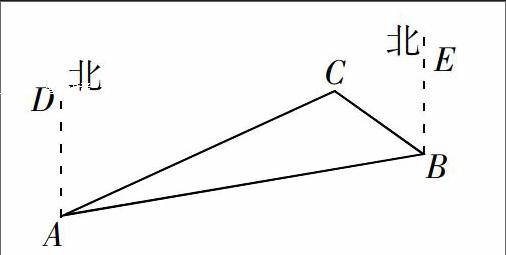
如下图，C岛在A岛的北偏东50°方向，B岛在A岛的北偏东80°方向，C岛在B岛的北偏西40°方向，从C岛看A、B两岛的视角∠ACB是多少度？

教师给出引领解题思路，学生动笔演练.最后教师给出规范化解题过程.

【设计意图】从学生已有的知识出发，结合本节课的学习内容，给学生提供有针对性、有创意的练习题，激发学生的学习兴趣，引导他们在做练习的过程中，自主探索来巩固知识和获得技能，掌握基本的数学思想方法，感受数学研究的思想.

四、学以致用，加深理解

1. 在△ABC中，∠A=35°，∠B=43°，则∠C= .

2. 在△ABC中，∠A∶∠B∶∠C=1∶2∶3，则该三角形是 .

3.在△ABC中，∠A=80°，∠B=∠C，求∠C的度数.

4.已知三角形三个内角的度数之比为1∶3∶5，求这三个内角的度数.

通过训练，让学生总结三角形内角和定理可以解决的问题有：

（1） 三角形的内角和等于180°；

（2） 知道两个角，求第三个角；

（3） 知道三个角的关系求三个内角.

五、课堂小结，布置作业

1. 本节课学习的主要内容.

（1） 三角形内角和定理：三角形的内角和为180°.

（2） 证明方法：将三角形的三个角为180°转化为一个平角或同旁内角互补.

（3） 辅助线的添加技巧：围绕将三角形的三个角为180°转化为一个平角或同旁内角互补，利用平行线的性质进行证明.

2. 作业布置.

（1）写出三角形内角和定理能解决哪些问题.

（2）写出用三角形内角和定理解决问题的基本步骤.

（3）教科书P76第4题.

【设计意图】总结回顾学习内容，初步学会反思.鼓励学生在独立思考的基础上，积极参与到对数学问题的讨论中来，敢于发表自己的观点，尊重理解他人的见解，在交流中获益.让学生明白本节课主要学习的重点难点问题，知道关键问题如何处理.endprint