蒙特卡罗法在某公路边坡可靠性分析中的应用

黄 东，匡 波（广西壮族自治区交通规划勘察设计研究院，广西 南宁 530029）

蒙特卡罗法在某公路边坡可靠性分析中的应用

黄 东，匡 波
（广西壮族自治区交通规划勘察设计研究院，广西 南宁 530029）

文章介绍了蒙特卡罗法的原理及模拟步骤，并采用该方法对某高速公路K146+300右边坡防护前后的稳定性进行了可靠性分析。计算结果表明，边坡的破坏概率由支护前的20.69%降为支护后的4.63%，边坡由低危险性提高至稳定，边坡加固措施合理有效。

公路；边坡；蒙特卡罗法；可靠性分析；破坏概率；应用

0 引言

传统的边坡稳定性分析及边坡防护设计中，往往采用确定性方法得到一个稳定安全系数定值。实际上，由于受钻探取样、室内试验、岩体性质等多方面的不确定性，确定性分析一定程度上并不能反映边坡的安全程度。

而边坡可靠度理论可以很好地解决这种不确定性问题。一般可通过经验判断或敏感性分析，确定变异性较大的因素，然后以此作为随机变量，对边坡进行可靠性分析，其结果包括边坡的平均安全系数以及边坡的破坏概率。当破坏概率小至工程上能够接受的程度，则表明边坡是安全的。相对安全系数而言，破坏概率更能客观、定量反映边坡的安全性［1］。

边坡可靠性分析方法有很多种，包括蒙特卡罗法、一次二阶矩法、Rosenbluth点估计法、可靠性指标优化迭代法、随机有限元法［3］［4］等。其中蒙特卡罗法应用相对比较广泛，是目前可靠性分析中比较精确的方法［5-8］。

本文结合蒙特卡罗法，对某高速公路K146+300右侧边坡在防护前后的稳定性进行可靠性分析。

1 蒙特卡罗法［1］［2］

1.1 基本原理

蒙特卡洛的基本原理是：把边坡安全系数定义为状态函数：

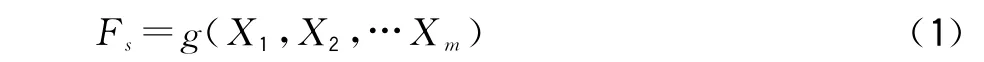
其中X1，X2，…，Xm为具有一定概率分布的独立状态变量，通过随机从Xi中抽取同分布状态变量X′1，X′2，…X′m，则由（1）式能计算出状态函数的一个随机样本F′，用同样方法可产生N个安全系数样本。根据边坡极限状态条件为Fs=1，因此，如果这些产生的样本中有M个满足Fs≤1，当N够大时，可认为边坡破坏概率为：

同时，根据获取的N个安全系数值，可求出其均值及标准差，并得到可靠性指标：

1.2 模拟步骤［1］［9］

以下为具体模拟步骤：

（1）选择边坡分析典型断面，根据钻探及边坡调绘结果，确定边坡工程地质剖面，定性分析边坡可能的破坏模式。

（2）通过经验判断及敏感性分析，确定可靠性分析的随机变量，从而建立边坡可靠性分析模型。在此基础上，确定随机变量的概率分布。一般岩土体强度参数是影响边坡稳定的关键性指标。

（3）确定边坡最易出现失稳的潜在滑动面。潜在滑动面一般由以下两种方法得到：①通过钻探及地质调绘，寻找边坡控制性不利结构面，确定边坡潜在滑动面；②边坡岩土体为均质体、边坡无单一不利控制结构面时，可通过试算搜索确定安全系数最小的最危险滑动面。

（4）确定随机变量的分布类型。

（5）对随机变量随机抽样一组同分布的随机数，由式（1）计算一个安全系数样本。

（6）重复（5）N次，直到精度满足要求。

（7）拟合安全系数的概率分布，求得其均值、标准差、破坏概率及可靠指标，以此判断边坡是否安全。

通常，根据表1，可将边坡稳定等级划分为五类（见表1）［10］。

表1 边坡岩体参数统计分布表

2 实例分析

某高速公路K146+300右侧路堑高边坡共五级，坡型采用台阶式，每隔10m设置一道边坡平台，平台宽2m，从下往上，边坡设计开挖坡率分别为1∶0.75、1∶1、1∶1、1∶1.25、1∶1.5，边坡最大开挖高度约50m。边坡主要由三叠系全～强风化泥岩和弱风化泥岩组成，该边坡附近发育一大断裂带，受构造挤压影响边坡岩体十分破碎，呈碎裂状结构。整个坡体内无控制性节理面。边坡第一、二级采用500kN锚索锚固，总长分别为20m、25m，第三、四级采用50kN锚杆中浅层加固，长8m。

2.1 随机变量的选择及可靠性分析类型

选择边坡主要岩土层的粘聚力c、内摩擦角φ以及地下水位作为随机变量，其中边坡岩土强度参数分布见表2。

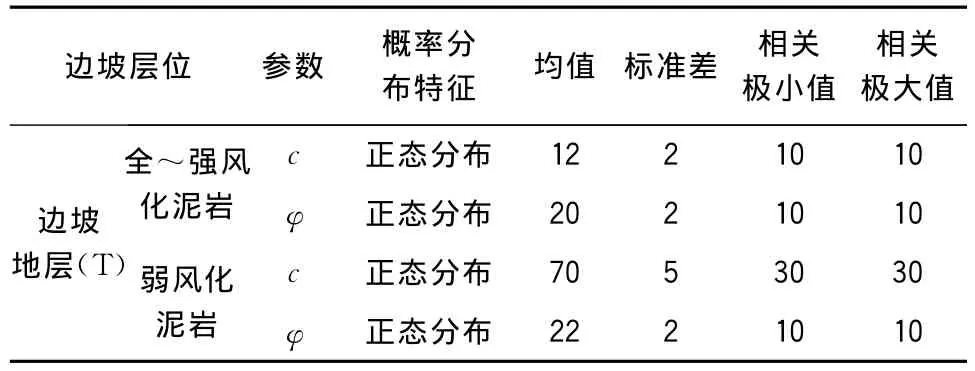
表2 边坡岩土体参数统计特征量表

2.2 可靠性分析

根据边坡定性分析，边坡可能出现圆弧滑动。本文采用Bishop圆弧法搜索，确定边坡最危险的潜在滑动面。采用蒙特卡罗法取样，取样数N=10 000。对未防护前及防护后的边坡进行可靠性分析。按1.2步骤和方法，便可计算出该边坡的可靠性分析结果。如图1所示。

根据计算，边坡防护后，其安全系数由1.096提高至1.213，满足规范要求；边坡破坏概率由20.69%降为4.63%，边坡由低危险性等级提高为稳定，进一步表明边坡经锚固防护后已趋于安全稳定。

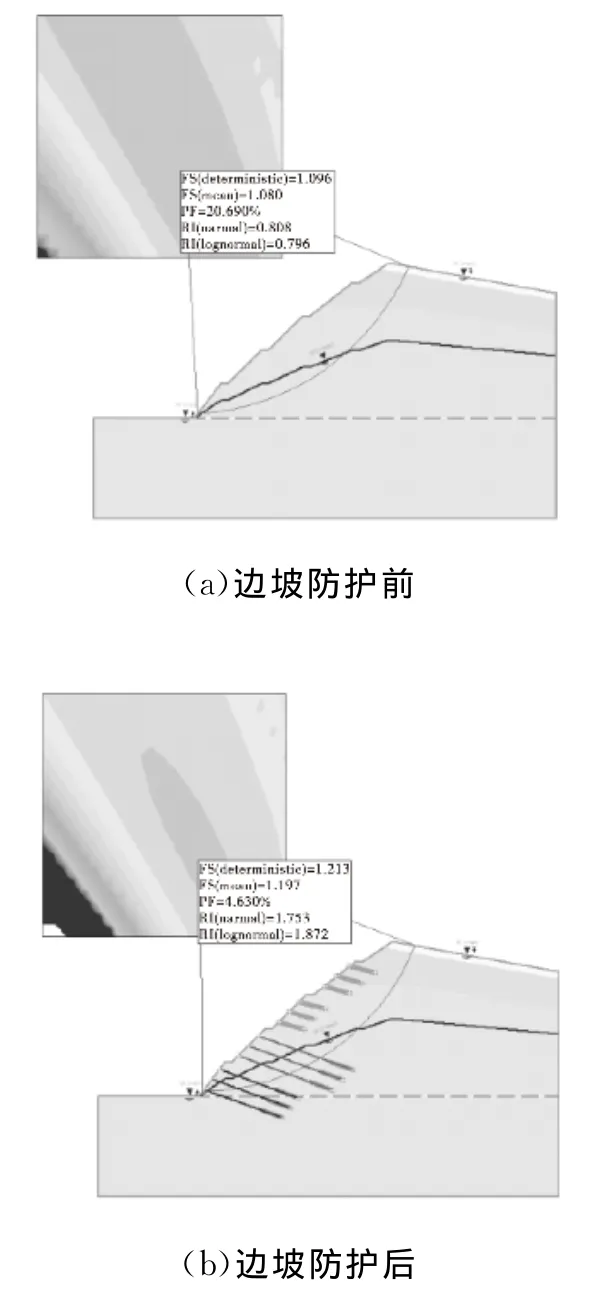
图1 边坡可靠性分析结果示意图

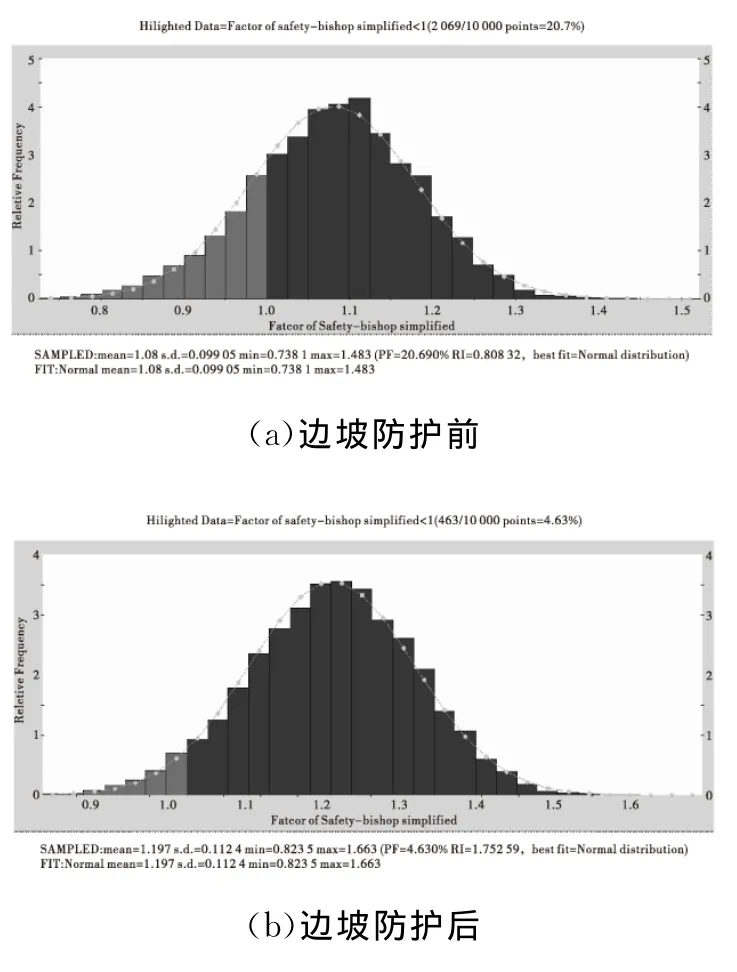
图2 安全系数分布直方图

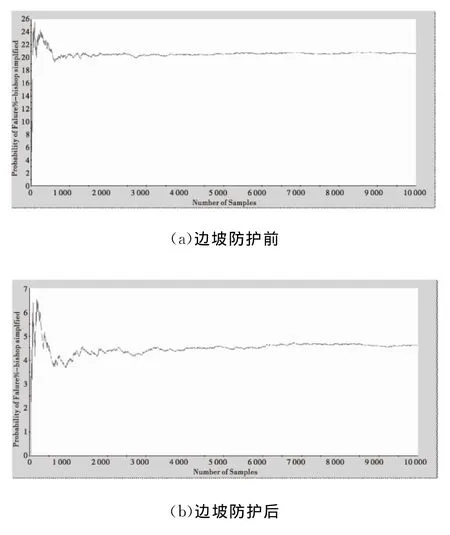
图3 边坡破坏概率收敛曲线图

由图2直方图可知，边坡防护后，安全系数呈正态分布，其平均值为1.197，标准差为0.112，安全系数变化范围0.823～1.663。由图3可知，本次可靠性分析所取样本数量偏大，实际当N=4 000时，破坏概率已基本收敛稳定。

3 结语

（1）介绍了蒙特-卡罗模拟法的原理及模拟步骤；

（2）采用蒙特-卡罗模拟法，对某高速公路K146+300右边坡进行了可靠性分析。边坡加固后，边坡破坏概率由支护前的20.69%降为支护后的4.63%，支护后的边坡满足稳定要求，为支护措施的合理布置提供了一定的依据。

［1］祝玉学.边坡可靠性分析［M］.北京：冶金工业出版社，1993.

［2］石丙飞.广州科学城林语山庄人工高边坡稳定性评价及设计研究［D］.长春：吉林大学，2006.

［3］罗文强，黄润秋，张倬元.斜坡稳定性概率分析的理论与应用［M］.北京：中国地质大学出版社，2003.

［4］刘 宁.可靠度随机有限元法及其工程应用［M］.北京：中国水利水电出版社，2001.

［5］匡 波，付宏渊，付传飞，等.基于广义Hoek-Brown准则的节理岩质边坡可靠性分析［J］.中外公路，2009（3）：58-61.

［6］袁 景，张秀丽.基于Monte-CarIo方法的边坡可靠度分析［J］.辽宁工程技术大学学报，2005，24（增）：10-12.

［7］熊赞民，高全臣，王春来.SLIDE在深基坑支护可靠性分析中的应用［J］.矿业研究与开发，2008，28（2）：3-4.

［8］王正国，田小宝.边坡可靠性的Monte-CarIo分析［J］.中国矿业，1999，48（8）：11-15.

［9］何朋朋.基于蒙特卡罗方法的边坡可靠性分析［D］.北京：中国地质大学硕士学位论文，2006.

［10］徐卫亚，张志腾.滑坡失稳破坏概率及可靠度研究［J］.灾害学，1995，10（4）：33-37.

Application of Monte Carlo Method in Reliability Analysis of A Highway Slope

HUANG Dong，KUANG Bo
（Guangxi Communications Planning Surveying and Designing Institute，Nanning，Guangxi，530029）

This article introduced the principle and simulation step of Monte Carlo method，and used thismethod for the reliability analysis on the stability of the right slope at a highway K146+300before and after the protection.The results showed that the slope failure probability is reduced to 4.63%after the support from 20.69%before the support，increasing to the stabilized slope from low-risk slope，thus the sloperein-forcement measure is reasonable and effective.

Highway；Slope；Monte Carlo method；Reliability analysis；Failure probability；Application

U416.1+4

A

10.13282／j.cnki.wccst.2015.09.011

1673-4874（2015）09-0039-03

黄 东（1967—），高级工程师，主要从事公路勘察设计研究工作；

匡 波（1983—），工程师，主要从事公路勘察设计研究工作。

2015-05-10