高校信息类专业线性代数的拓展教学
2015-08-28刘笑嶂
刘笑嶂

【摘要】针对线性代数课程较强的抽象性和难以学习的特点,提出信息类本科专业的线性代数课程的拓展教学方法,并在人脸识别、搜索引擎排序两种应用背景下给出了拓展教学案例的要点,强调学以致用,以应用促学习的教学理念,有利于提高学生的学习兴趣和创新能力。
【关键词】信息类专业 线性代数 拓展教学
【中图分类号】O151;G424 【文献标识码】A 【文章编号】2095-3089(2015)08-0135-02
1.引言
在高等院校通信、电子、计算机等信息类本科专业的授课计划中,线性代数是一门非常重要的基础理论课程。线性代数的方法也是该类专业的研究生进一步深造和从事科研工作必备的基本技能。另外,线性代数还具有很强的逻辑性与抽象性,对培养学生的抽象思维能力、计算能力和解决实际问题的能力发挥着重要的作用。传统的教学法偏重理论的系统性,按照授课大纲讲授定义、引理和定理,再运用定理求解与之相对应的例题。这种教学方法使得学生很难深入理解定义、引理和定理的内涵与外延,更难做到知识点的扩展、应用和融会贯通。在这种情况下,最好的教学效果就是学生學会如何解决习题。然而在实践中,这种枯燥的定义—定理—习题的教学模式让相当一部分学生失去了学习兴趣,从而使多数学生以应付考试为学习线性代数的目的,更不能奢望其发挥学生的主观能动性、提高学生的创新能力了。近年来,作者从自身的教学经验和科研经历体会到,在线性代数的教学中应该强调学以致用的观点,并对信息类本科专业的线性代数课程腾出专门的课时进行拓展教学,引导学生通过应用实例理解相关的定义和定理,不但提高了学生的学习兴趣,还有效地促进了学生对线性代数理论和方法的掌握。
2.两个拓展教学案例的要点
(1)人脸识别中的矩阵运算
人脸识别是基于人的脸部特征信息进行身份识别的一种生物识别技术,是用摄像机或摄像头采集含有人脸的图像或视频流,并自动在图像中检测和跟踪人脸,进而对检测到的人脸进行识别的一系列相关技术。人脸识别产品已广泛应用于金融、司法、军队、公安、边检、政府、航天、电力、工厂、教育、医疗及众多企事业单位等领域。随着技术的进一步成熟和社会认同度的提高,人脸识别技术将应用在更多的领域。作者在教学实践中发现信息类专业的大学生对人脸识别抱有极大的关注热情。
人脸识别的理论丰富、方法多样,但特征脸[1]方法被认为是第一种有效的人脸识别方法。对本科生解释特征脸方法背后的线性代数思想,只需讲清以下要点即可。
第一,将分辨率为rxc的人脸图像的每一列的像素串联在一起,产生一个高维(维数D=rc)的向量,这样每个图像被视为一个向量,N个人脸图像的集合就成了D维向量集{x1,x2,……xN}。
第二,计算向量集的均值向量
第三,协方差矩阵S显然是个正定的实对称矩阵,而实对称矩阵总是可以单位正交对角化的,即S=V?撰VT,其中V=(v1,v2,…,vD)的D个列向量是S的单位正交的特征向量,?撰=diag(?姿1,?姿2,…,?姿D)是以S的D个特征值为对角元的对角矩阵,特征值的大小满足关系?姿1≥?姿2≥…≥?姿D>0,并且特征向量vd与特征值?姿d对应,d=1,2,…,D。舍弃较小的特征值对应的特征向量,与较大特征值对应的特征向量{v1,v2,…,vm}(m在使用特征脸方法进行人脸识别时,只需要如上求出每个人脸对于一组特征脸的表出系数,利用表出系数向量按照就近原则对人脸分类。
(3)搜索引擎Google排序的矩阵原理
Google创始人Larry Page和Sergey Brin于1997年构建早期的搜索系统原型时提出了能够自动判断网页重要性的链接分析算法PageRank[2],自从Google在商业上获得空前的成功后,该算法也成为其他搜索引擎和学术界十分关注的计算模型。这个问题必然引起信息类专业大学生的极大兴趣。
网络的本质就是超链接。一个网站总是尽量与某些重要的站点相链接,相当于这个网站投了对方一票。当成百上千个网站链接到一个站点时,可以认为这个站点是一个很重要的站点。PageRank就是基于“从许多优质的网页链接过来的网页,必定还是优质网页”的回归关系,来判定所有网页的重要性。PageRank为每个网页计算等级值,并在显示搜索结果时按照等级值对网页排序。
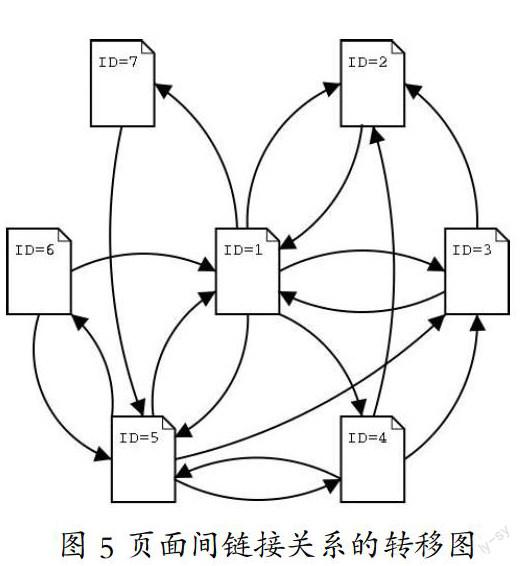
可以用一个简单的例子来说明PageRank算法。假设7个HTML文件之间的链接关系如图5所示。这些HTML文件间的链接关系是闭合的,也就是说,除了这些文档以外没有其他任何链接的出入。
3.结论与认识
教学方法应该结合学生的实际情况,因材施教。只有设法帮助学生理解教学内容,使教学变得直观、具体,加深学生的感性认识和直观印象,才能激发学生的学习兴趣和积极性。
通过信息类专业线性代数的拓展教学,可以将抽象概念形象化,激发学生学习的兴趣,加深基础理论的理解和掌握;同时通过相关案例的教学,使学生将学习时间由课堂自然延伸到课后,发挥了自主学习的能动性,培养了学生的科研能力。
参考文献:
[1]Turk M, Pentland A. Eigenfaces for recognition [J]. Journal of Cognitive Neuroscience,1991, 3(1):71-86.
[2]Lawrence Page, Sergey Brin, Rajeev Motwani, Terry Winograd. The PageRank Citation Ranking: Bringing Order to the Web [R]. Technical Report. Stanford InfoLab 1998.
[3]James Keener. The Perron–Frobenius theorem and the ranking of football teams[J]. SIAM Review (SIAM), 1993, 35 (1): 80-93.
