孔隙介质渗透力的细观数值解析

蒋中明,王 庆,秦卫星

(长沙理工大学水利工程学院,湖南 长沙 410004)

孔隙介质渗透力的细观数值解析

蒋中明,王 庆,秦卫星

(长沙理工大学水利工程学院,湖南 长沙 410004)

为深入理解孔隙介质中的渗透力概念,分析了渗透力的力学本质,明确了渗透力的定义。从细观角度分析了渗流条件下土颗粒受力特点以及PFC3D对单一颗粒在渗流条件下的渗流作用力计算方法,建立了渗透力数值计算的细观颗粒流分析模型,利用PFC3D的流固耦合分析功能,研究了渗流条件下孔隙介质土体渗透力特性及数值大小。渗透力数值解与解析解对比分析结果表明:采用基于细观理论的PFC3D研究孔隙介质在渗流条件下的宏观受力特点是可行的;渗透力由所有土颗粒表面的法向应力和黏滞切向力合成。

孔隙介质;渗透力;细观力学;土力学; PFC3D;数值分析

渗透力是土力学中非常重要的基本概念,是引起涉水边坡及滑坡产生灾害性失稳的重要因素之一;同时渗透力也是引起坝基及基坑渗透变形的直接因素。如何认识、理解和应用岩土介质中水流运动引起的“渗透力”,在国内引起广泛持久的讨论[1-4]。关于渗透力的概念,不同研究者给出了具有一定差异化的定义[5-9],如钱家欢等[5]将渗透力称作“动水力”;丰定祥等[6]认为动水压力就是渗透力;Li等[7]则认为渗透力就是拖曳力。在对渗透力定义不同的前提下,其计算公式也应该各不相同，但几乎所有的研究得到的渗透力计算公式均为J=iγfV,都是基于一定的力学概化模型通过解析推导得到的[5-9],推导过程有的复杂,有的简单。尽管在概念上存在差异性,不同的学者却采用不同方法得到了相同的渗透力计算公式,给人们正确理解渗透力的概念带来了困难。从本质上讲,作用在土体上的渗透力实质上是作用在土体所有颗粒上的流体作用力的综合宏观反映,而目前渗透力宏观分析时研究对象的选择不统一是造成渗透力推导过程多样化和复杂化的根本原因。由于对渗透力本质的理解不深入,导致我国部分科技人员在边坡稳定性分析中计算渗透力的作用时出现了一定的误区[10-11]。文献[12]将“单位体积土颗粒所受到的渗透水流作用力称为渗透力”,笔者认为这种定义更具科学性。目前人们对渗透力的计算与分析多是从宏观角度进行,为更好地理解渗透力的概念,本文从土体颗粒组成的细观角度出发,研究孔隙水流对土颗粒所产生的作用力,进一步论证渗透力概念所包含的内涵及宏观解析计算公式的合理性。

1 渗透力解析的细观数值计算理论

土体由三相组成,即固相、液相和气相，当土体处于完全饱和时,土体由固液两相组成。孔隙水的存在使得人们在分析土体受到的作用力时,需要考虑孔隙水对土体骨架的作用效应。土体中水在静止和运动(渗流)条件下的作用力效应分别采用浮力和渗透力来描述。通过对国内外文献的深入分析,笔者认为将渗透力定义为土体中水的流动对土骨架所施加的作用力是科学合理的。土中水的渗流作用力包含了由作用在固体骨架上的法向面积力及切向黏滞力(摩擦阻力)两部分,这两种力实际上是从细观角度对渗流力学效应加以描述,即在服从达西定律的条件下,渗流作用力可概括为垂直于颗粒周界表面的法向压力和与颗粒表面相切的水流摩擦剪应力的合成[12]。对任意颗粒表面上的力进行积分后,作用在颗粒表面的法向压力和流体摩擦剪应力可用两个向量f0p和f0f代表,其合力为f0。 此合力f0可称为渗流作用力,该力作用到每个颗粒上的大小和方向各有不同。如果考虑体积为V的土体,则可将其中各土粒所受的力几何相加再除以体积即得单位体积土体中固相颗粒所受的渗流作用力(acting force of seepage)为

(1)

由此可见,渗透力完全可以定义为单位体积土体中固相颗粒所受的渗流作用力。从细观角度,很容易理解渗透力由作用在颗粒表面的法向面积力及切向黏滞力这两种不同性质的力组成。事实上,在细观分析理论及分析软件不成熟之前,从细观角度对土体(复杂颗粒集合体)渗透力按式(1)求解是困难的。现阶段基于细观理论的颗粒流分析软件(PFC3D)的完善与发展,为渗透力的细观分析奠定了基础[13]。为了进一步理解渗透力的来源及构成,下面采用PFC3D软件从细观层次来分析渗流条件下流体对固体颗粒的作用力大小。在PFC3D中,流体对颗粒的作用力定义为驱动力(driving force),该驱动力的实质与文献[12]中提到的渗流作用力(即渗透力)是一致的。

图1为流体在颗粒集合单元体中流动示意图。

图1 流体在颗粒集合单元体中流动示意图[13]

假定流体流动发生在x方向,且x方向的流体压力梯度为dp/dx,考虑单元体内颗粒在x方向的力平衡,则作用在所有颗粒上的驱动力之和fdsum为

(2)

式中:fintx为单位体积内固体颗粒与流体之间的相互作用力(实质就是流体对固体颗粒的拖曳力,或固体颗粒对流体的流动黏滞阻力);dpi为颗粒直径;np为研究单元体内的颗粒数量。式(2)右边第一个负号表示施加在流体上的力为正,右边第二项代表由压力梯度dp/dx作用在颗粒上的力,负号表示压力沿流动正方向(x轴正向)减少。

一般地,当考虑流体在任意方向上流动时,作用在颗粒上的渗透力可用下式表达

(3)

式中n为孔隙率。

2 渗透力细观数值解析

为了说明孔隙水压力差作用下渗流引起的渗透力及其数值大小,选取长、宽和高分别为100 mm、30 mm和30 mm的长方体区域进行研究。

a. 计算模型:研究域内充填3 108个直径在1.6～5 mm之间的小球(土颗粒),颗粒中间充满流体(水),流体可以在x=100 mm位置处排出。流体单元数量为250个。图2为所述饱和孔隙介质颗粒流分析的三维模型,图中右边界上的网格线为流体计算网格。

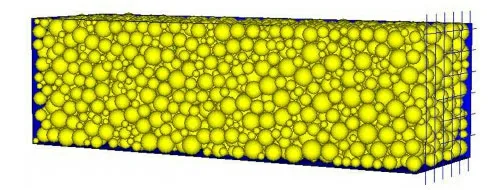
图2 饱和孔隙介质颗粒流分析三维模型

b. 流体计算边界条件:在左边界(x=0 mm)处施加的水压力为2 kPa,右边界(x=100 mm)处的压力为0 kPa;左右边界之间的水力梯度为2.038 736(按重力加速度9.81 m/s2换算)。计算域内小球与计算边界面之间设置滑动边界条件(即不考虑小球与边界之间的摩擦作用)。

c. 计算参数: PFC3D颗粒流流固耦合分析采用的计算参数见表1。

表1 计算力学参数

对于上述数值模型,在不考虑重力加速度作用前提下,作用在每一个颗粒上的力均来自该颗粒所在部位的孔隙水压力差以及水流动所产生的拖曳力,两者之和就是渗透力,该渗透力直接作用在该颗粒上。图3给出了流速矢量及颗粒接触压力分布。由图3可知,研究域内固体颗粒之间的接触压力在渗流方向明显大于其他两个方向,非渗流方向上的颗粒接触压力并不为零。孔隙中水流运动的总体方向为沿压力减小(水头降低)的方向,孔隙中局部水流方向并非完全与渗流方向(x正方向)一致。

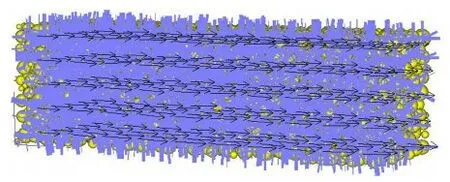
图3 流速矢量及颗粒接触压力分布

经过对数值计算结果的分析可以得到:研究域的孔隙率为0.406,渗透系数为6.188×10-3cm/s。研究域内颗粒受到的渗透力数值计算结果为1.766 886 N,其中沿x方向的渗透力为1.766 874 N,沿y方向的渗透力为2.139 871×10-3N,沿z方向的渗透力为6.139 831×10-3N。由此可见,对于由大小不一的颗粒构成的土体孔隙介质而言,渗流对固体骨架的作用力是多方向的。总的来说,渗流对骨架的主要作用力方向为渗流方向。这一点可以从渗流计算结果中看出。

根据渗透力的计算公式,渗透力的大小是以整个土体占据的空间来计算的。对于本数值算例,作用在100 mm×30 mm×30 mm长方体区域上的渗透力大小为J=iwγwV=1.80 N。

上述渗透力计算公式中水力梯度iw为根据计算模型左右端边界上的压力计算得到的平均水力梯度。对比数值解和解析解的结果可以发现,数值解的结果(1.766 886 N)略小于解析解(1.80 N),其原因是多方面的,但两者的相对误差仅为1.83%,因此数值仿真方法可以很好地模拟固体颗粒受到的水流驱动作用。数值解和解析解结果的高度一致性,揭示了渗透力是作用在颗粒表面上的法向压力和黏滞剪切力合成作用结果的这一内涵,再次说明了将渗透力定义为土体中固相颗粒所受的渗流作用力是科学、合理的。

3 流体黏滞性对渗透力的影响

孔隙中的流体,有时不仅仅是液态水,也可能是黏滞性更大的石油等流体。为了分析孔隙中的流体性质对渗透力的影响,将上述数值模型中的孔隙流体更换为原油进行分析。相关计算参数为:原油密度为850 kg/m3,运动黏滞系数取0.01 Pa·s,其余条件不变。计算结果表明,当孔隙中流体介质为石油时,由于其黏滞性相对较大,计算得到的石油流动的渗透系数小于水的渗透系数,其值为5.997×10-3cm/s。孔隙中原油流动形成的渗透力为1.786 123 N,其中沿x方向的渗透力为1.785 156N,沿y方向的渗透力为3.302 024×10-3N,沿z方向的渗透力为5.866 871×10-2N。由此可见,当填充在孔隙中的流体为黏滞性更大但密度更轻的流体时,孔隙介质骨架受到的渗透力略大于充填介质为水时的渗透力,但渗透力增加幅度不大,约为1.1%。

孔隙中的流体为石油时,根据渗透力计算公式有J=ioilγoilV=1.80N,其中ioil为按照石油密度换算的“水力梯度”,当计算域两端的压力差为2 kPa时,其 “水力梯度”为2.398 513,大于按水体计算得到的水力梯度值2.038 736,相差幅度达到了17.65%。同样,当孔隙流体为石油时,渗透力数值计算结果也略小于解析解结果,两者误差约0.77%。

对比孔隙流体为水和石油两种介质条件下的结果,可以发现当作用于孔隙介质不同位置上的压力差一致时,尽管水和油的黏滞性不同,但由于水和油的容重也不相同,因此所形成的水力梯度不相同,最终导致渗透力的大小基本一致。

4 结 论

a. 渗透力是孔隙介质骨架在渗流过程中受到的流体作用力,它由所有颗粒表面上的法向压力和黏滞剪切力合成。

b. 渗透力的细观数值仿真计算结果表明,渗透力计算公式采用包含孔隙在内的土体体积进行计算是可行的。渗透力在宏观层次上作为“体力”是一种“等效体积力”,在细观层次上其本质仍然是作用在颗粒表面上的面力。

[1] 毛昶熙,李吉庆,段祥宝.渗流作用下土坡圆弧滑动有限元计算[J].岩土工程学报,2001,23(6):764-752.(MAO Changxi,LI Jiqing, DUAN Xiangbao.Finite element calculation on circular slip of earth slope under seepage action[J]. Chinese Journal of Geotechnical Engineering,2001,23(6):764-752.(in Chinese))

[2] 沈珠江.莫把虚构当真实:岩土工程界概念混乱现象剖析[J]. 岩土工程学报,2003,25(6):767-768.(SHENG Zhujiang.No confusing fiction with reality-analysis of misunderstanding of some concepts in geotechnical engineering[J].Chinese Journal of Geotechnical Engineering,2003,25(6):767-768.(in Chinese))

[3] 刘晓,唐辉明,罗红明,等.对滑坡防治工程相关规范中渗流问题的研究[J].岩土力学,2009,30(10):3173-3181.(LIU Xiao,TANG Huiming, LUO Hongming,et al.Study of seepage flow for Chinese design codes of landslide stabilization[J]. Rock and Soil Mechanics,2009,30(10):3173-3181.(in Chinese))

[4] 陈津民.土中渗透力的定义和论证[J].岩土工程界,2008,11(10):22-24.(CHEN Jinmin. Definition and discussion about seepage force in soil[J].Chinese Journal of Geotechnical Engineering,2008,11(10): 22-24.(in Chinese))

[5] 钱家欢,殷宗泽.土工原理与计算[M].北京:中国水利水电出版社,2003.

[6] 丰定祥,吴家秀,葛修润.边坡稳定性分析中几个问题的探讨[J].岩土工程学报,1990,12(3):1-9.(FENG Dingxiang,WU Jiaxiu,GE Xiuru. Some problems of slope stability analysis[J].Chinese Journal of Geotechnical Engineering,1990,12(3):1-9. (in Chinese))

[7] LI X S,MING H.Seepage driving effect on deformations of San Fernando dams[J].Soil Dynamics and Earthquake Engineering,2004,24(12):979-992.

[8] 党进谦,李法虎.土力学[M].北京:中国水利水电出版社,2013.

[9] 袁聚云,钱建国,张宏鸣,等.土质学与土力学[M].北京:人民交通出版社,2009.

[10] 曹剑波,贾洪彪,曾川川.边坡稳定性分析中水作用力计算方法研究[J].路基工程,2010(2):124-126.(CAO Jianbo, JIA Hongbiao,ZENG Chuanchuan.Study on calculation method of water active force in slope stability analysis[J].Subgrade Engineering,2010(2):124-126.(in Chinese))

[11] 魏海涛,李远.渗流边坡安全系数计算中的水土分算与水土合算误差分析[J].建筑科学,2011,27(9):41-43.(WEI Haitao,LI Yuan. Error analysis in safety coefficient calculation of side slope in seepage condition between the effective stress method and the total earth pressure method[J].Building Science, 2011,27(9):41-43. (in Chinese))

[12] 毛昶熙,段祥宝.关于渗流的力及其应用[J].岩土力学,2009,30(6):1569-1575.(MAO Changxi,DUAN Xiangbao.On seepage forces and application[J].Rock and Soil Mechanics,2009,30(6):1569-1575.(in Chinese))

[13] Online Manual of PFC3D Particle Flow Code in 3Dimensions [R]. Minneapolis, MN:Itasca Consulting Group, Inc.,2006.

Numerical interpretation of seepage force in porous media based on micromechanics//

JIANG Zhongming, WANG Qing, QIN Weixin
(SchoolofHydraulicEngineering,ChangshaUniversityofScienceandTechnology,Changsha410004,China)

In order to deeply understand the concept of seepage force in porous media, its mechanical essence is analyzed and its definition is exactly given. From the perspective of micromechanics, the mechanical characteristics of soil particle under percolation condition is analyzed, and the calculation method of singular particle’s seepage force under percolation condition employed in particle flow code in three dimensions(PFC3D) is discussed. Additionally, the analysis model of mesoscopic particle flow for calculating seepage force value is built. By using the fluid-solid coupling analysis function of PFC3D, the features and values of soil seepage force of porous media under percolation condition are studied. Through comparing the value of seepage force obtained by numerical method with that by analytical solution, the results indicate that it is feasible to study the macro-characteristics of driving force in porous media under percolation condition with PFC3D, which is based on mesoscopic theory. Moreover, the seepage force is a synthesis result of normal stress and shear viscous stress acting on the surface of soil particles.

porous media; seepage force; micromechanics; soil mechanics; particle flow code in three dimensions(PFC3D); numerical analysis

水能资源利用关键技术湖南省重点实验室开放研究基金(PKLHD101305)

蒋中明(1969—),男,重庆人,教授,博士,主要从事岩土工程稳定性研究。E-mail: zzmmjiang@163.com

10.3880/j.issn.1006-7647.2015.04.009

TU441+.33

A

1006-7647(2015)04-0035-04

2014-04-08 编辑：熊水斌)