岩石裂隙中水流脉动压力传播的数值模拟
2015-08-28李爱华
李爱华,朱 江
(中国石油大学(华东)石油工程学院,山东 青岛 266580)
岩石裂隙中水流脉动压力传播的数值模拟
李爱华,朱 江
(中国石油大学(华东)石油工程学院,山东 青岛 266580)
为了分析网络结构对裂隙水体内脉动压力传播规律的影响,引入蒙特卡罗模拟方法,通过数值模拟得到与天然裂隙网络在统计上相似的仿真裂隙网络,以此作为裂隙水的赋存空间,建立一维瞬变流模型,对脉动压力在裂隙网络中的传播进行数值模拟,得出裂隙水中脉动压力传播的非定常时间过程,以及裂隙网络中压力脉动强度的空间分布云图。模拟结果表明,岩体裂隙网络中脉动压力的传播具有显著的各向异性,裂隙中各点的瞬时脉动压力是由该点所衔接(尤其是直接衔接)的裂隙线元的水力瞬变作用以及裂隙入口干扰源、裂隙末端反射源三者共同作用的结果。
脉动压力;裂隙网络;蒙特卡罗方法;瞬变流模型;数值模拟
冲击射流的脉动压力在缝隙中的传播是导致溢洪道衬砌板块揭底破坏的主要原因。1992年Fiorotto等[1]提出板块缝隙中脉动压力传播的瞬变流模型,现已被广泛应用于脉动压力传播的数值研究中[2-7]。Jia等[8-10]对缝隙中的脉动压力传播进行了试验研究。但无论是试验研究还是数值研究均局限于简单一维规则裂隙或者二维规则裂隙面内,并没有涉及实际基岩的复杂结构特性。Annandale[11]在1995年力图从水力和地质两个方面研究工程土石料的抗冲特性,定义了与土石料的强度、颗粒尺度、不连续性等相关的抗冲刷系数。但归根结底,抗冲刷系数是由经验系数确定的,同样没有涉及岩体的内部网络结构。
事实上,岩体是由岩块和分割岩块的裂隙网络所组成的结构体。岩体裂隙网络可以作为水体的赋存空间,因此裂隙网络的结构特性——如岩块结构面密度、粗糙度、开度、填充情况等,在很大程度上决定了岩体裂隙介质中水流脉动压力传播的特殊性和复杂性。岩体复杂裂隙网络的提出始于对地下水渗流的研究,用于解决工程中的裂隙岩体渗流问题。国内潘别桐等[12-13]在统计学和概率论基础上提出了基于蒙特卡罗(Monte-Carlo)模拟技术的结构面二维、三维裂隙网络模拟方法,该法可以综合反映裂隙系统的极不均匀性、渗透水流的各向异性和局部非连续性,还可以描述裂隙中水流瞬时变化的特征,因此可以应用裂隙网络模拟技术来研究岩体裂隙中压力波传播等问题。蒙特卡罗模拟技术现已被广泛应用于裂隙渗流研究领域[14-15]。
本文通过引入蒙特卡罗方法,模拟生成与天然岩体裂隙网络在统计上相似的仿真裂隙网络,并以此作为水体赋存空间,建立一维瞬变流模型,对裂隙水体中脉动压力的传播过程和分布规律进行数值模拟和分析。在对裂隙水流脉动压力波传播规律的研究中,引入蒙特卡罗方法,对于考察岩体裂隙结构对脉动压力传播的影响具有重要意义。
1 岩体裂隙网络的蒙特卡罗模拟
大自然中的岩体裂隙可划分为以下4个等级:①一级,真实裂隙网络——规模较大的断层、断裂和软弱夹层;②二级,随机裂隙网络——分布具有随机性的次一级裂隙网络;③三级,等效连续介质体系——规模较小、数量众多且分布密集的小裂隙;④四级,连续介质体系——岩块内的孔隙网络。在水利工程中,对一级真实裂隙需要进行特殊处理;三、四级裂隙规模较小,在渗流研究中通常作为等效的连续体或连续体处理。因此,本文研究基岩裂隙中脉动压力的传播以二级随机裂隙网络作为研究对象。
由于天然岩体在漫长的地质历史时期中遭受多期地质构造运动,裂隙网络具有特殊的随机性和不确定性。近些年发展起来的岩体裂隙网络的计算机模拟是岩体结构定量研究的最佳途径。裂隙网络的模拟过程与现场实测统计过程恰好相反,现场测量统计是根据岩体中裂隙的分布形式求出表征裂隙的各种几何参数的分布函数,而计算机模拟过程是根据统计得出的裂隙几何参数的分布函数来推求服从这些分布规律的裂隙网络图形,因此,模拟是实测的逆过程。蒙特卡罗法是根据现场结构面统计测量得出的参数分布来生成各参数的(伪)随机数,进而产生一个与真实岩体结构在统计上相似的结构面网络图形。
岩体裂隙的基本几何参数包括裂隙密度、裂隙空间产状(裂隙走向、裂隙倾向、裂隙倾角)、裂隙间距以及裂隙迹线长等。裂隙几何特性见图1,裂隙的产状为NαE∠SEβ。

图1 岩体裂隙几何特性示意图
通常约定裂隙密度服从均匀分布,裂隙的倾向和倾角服从正态分布,裂隙迹线长服从正态分布、对数正态分布或者负指数分布中的一种。本文对满足表1裂隙统计分布的裂隙网络给出由蒙特卡罗模拟得出的二维仿真裂隙网络(图2),并对此仿真裂隙网络中的脉动压力传播特性进行瞬变流数值分析。

表1 模拟岩体10 m×10 m范围内裂隙统计分布规律
注:μ为平均值,σ为方差。
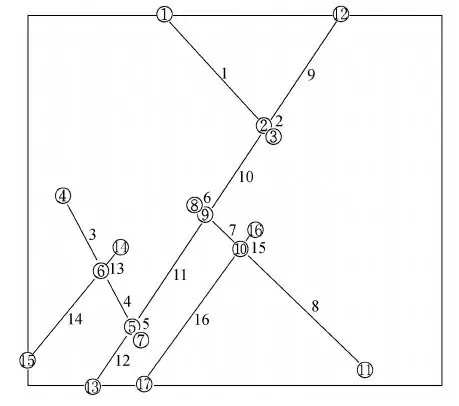
图2 仿真裂隙网络图形及其节点、线单元编号
由表1可见,模拟岩体10 m×10 m范围内有两组不同几何特征的裂隙,岩体顶端受射流水体冲击,左右两端为透水边界,底端设为不透水边界。
由图2可见,裂隙网络中有17个节点、16个线单元、0个回路,分形理论中称之为“树”。裂隙网络生成的同时,实现了:①去除网络中的孤立裂隙。若裂隙没有最终连通到干扰波源,即连通到控制体顶边界,则裂隙中不可能有干扰波的存在以及传播。这种裂隙称为孤立裂隙或者死裂隙,在研究中不予考虑。②裂隙网络中线单元及节点自动编号。③裂隙网络的矩阵表示:衔接矩阵——定义了裂隙节点与裂隙线单元之间的衔接关系和裂隙方向;几何参量矩阵——存放各条裂隙的厚度、粗糙系数以及堵塞系数等信息。
2 余弦干扰波在裂隙网络中的传播
以仿真裂隙网络作为水体赋存空间,研究其中脉动压力的传播规律。沿各条有向裂隙建立一维瞬变流模型:
(1)
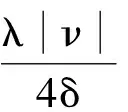

图3 不同节点的脉动压力时间过程
在裂隙网络节点1处,施加单一的余弦干扰波h=cos(2πft),其中f为干扰波频率,其最大脉动幅值为1.0 m水头。水工模型实验表明,在水垫塘底部,导致底板破坏的脉动压力波属于低频波,频带区位于0~10 Hz之间,这里取f=5 Hz。节点12处未感应到此干扰波。在此干扰源作用下,取空间步长为Δx=1 m,时间步长为Δt=Δx/a=0.001 s,用特征线-有限差分法离散求解各裂隙中的瞬变流双曲线方程。
图3分别给出节点1、节点9、节点5、节点13的脉动压力时间过程。图4给出了整个裂隙网络中,脉动压力强度(即方差)的分布云图。

图4 裂隙网络内脉动压力强度分布云图
由图3可以看出,当入口施加单一余弦干扰波时,干扰波将在极短时间内传播至岩体内各裂隙处。其时间过程曲线与干扰源时间过程曲线(图3(a))不同,是一条复杂的波动曲线。文献[6]对单体板块下缝隙中脉动压力传播的研究认为,这是由于缝隙中类似于水锤的水力瞬变作用导致的,而且水力瞬变的频率与缝隙长度密切相关。因此,在复杂裂隙网络中,不同长度裂隙可以导致不同频率的水力瞬变,裂隙中某点的脉动压力与其所直接衔接或者间接衔接(通过其他裂隙连通至该节点)裂隙的水力瞬变作用相关,直接衔接裂隙的水力瞬变影响尤其显著。
由图4容易得出:其一,裂隙网络中的脉动压力传播具有很强的各向异性特性,这主要取决于作为脉动压力传播介质的水体,其赋存的空间即岩体裂隙网络具有特殊的结构特性和不连续特性。其次,裂隙内某点的脉动强度与各裂隙单元的端点有关。裂隙单元的端点或为开口端(即紧邻透水层或裂隙延伸至控制体外),或为盲端(即紧邻不透水层或裂隙终止于岩体内部)。若裂隙末端为开口端,则裂隙内各处的脉动压力强度由此处与干扰源的等效距离决定。所谓等效距离是指沿裂隙结构面连通到干扰源的最短距离。一般而言,某点与干扰源的等效距离越近,则其脉动强度越强;反之,若某点与干扰波源的等效距离越远,则其脉动强度越弱。反映在图3上,节点9、节点5、节点13与干扰波源(节点1)的等效距离依次渐远,各点的脉动强度分别为0.43 m、0.37 m、0.26 m。若裂隙末端为盲端,当干扰波传至裂隙末端时,因存在壁面反射,使得其附近各点的脉动压力强度较大,且到反射源等效距离越小,反射效应对其影响越大。反映在图4上,裂隙单元8、16与裂隙单元9相比,虽然前者到干扰源的等效距离大,由于其所在裂隙的末端为盲端,致其压力的脉动强度远大于后者。裂隙14与控制体左边界相交,裂隙末端为开口端,因此其压力脉动强度急剧减小。
3 结 论
a. 复杂裂隙网络中的脉动压力传播具有很强的各向异性特性,与岩体裂隙网络的结构特性密切相关。
b. 当瞬时压力干扰波在裂隙网络中传播时,不同长度裂隙可以导致不同频率的水力瞬变。裂隙网络中某点的脉动压力时间过程为复杂的波动曲线,与该点所衔接(尤其是直接衔接)的裂隙线元的水力瞬变作用密切相关。
c. 岩体裂隙网络中某点的压力脉动强度不仅与此点离干扰波源的等效距离大小有关,而且与各条裂隙的端点条件有关,压力脉动强度受裂隙入口干扰源和裂隙末端反射源共同影响。到干扰源或者反射源的等效距离越小,受其影响越大。
[1] FIOROTTO V,RINALDO A.Fluctuating uplift and lining design in spillways stilling basins[J].Journal of Hydraulic Engineering,1992,118(4): 578-596.
[2] LIU Peiqing,LI Aihua.Model discussion of pressure fluctuations propagation within lining slab joints in stilling basins[J].Journal of Hydraulic Engineering,2007,133(6): 618-624.
[3] LIU Peiqing,LI Aihua.Fluctuating uplift acting on rock blocks at the bottom of river bed and estimation of the limiting scour depth[J].Journal of Hydraulic Research,2007,45(4): 478-485.
[4] LI Aihua,LIU Peiqing.Mechanism of rock-bed scour due to impinging jet[J].Journal of Hydraulic Research,2010,48(1): 14-22.
[5] 李爱华,刘沛清.脉动压力在消力池底板缝隙传播的瞬变流模型和渗流模型统一性探讨[J].水利学报,2005,36(10): 1236-1240.(LI Aihua,LIU Peiqing.Models for simulating the propagation of fluctuating pressure in gaps of stilling basin slab[J].Journal of Hydraulic Engineering,2005,36(10): 1236-1240.(in Chinese))
[6] 李爱华,王腾,刘沛清.溪洛渡坝区岩石河床冲刷过程数值模拟[J].水力发电学报,2012,31(5): 154-158.(LI Aihua,WANG Teng,LIU Peiqing.Numerical simulation of rock bed scour behind the dam of Xiluodu Hydropower Station[J].Journal of Hydroelectric Engineering,2012,31(5): 154-158.(in Chinese))
[7] 李爱华,刘沛清.脉动压力在板块缝隙中传播衰变机理研究[J].水利水电技术,2006,37(9): 33-37.(LI Aihua,LIU Peiqing.Study on mechanism of pulsating pressure propagation disintegration in joints of bottom slab[J].Water Resources and Hydropower Engineering,2006,37(9): 33-37.(in Chinese))
[8] JIA Y,KITAMURA T,WANG S S Y.Simulation of scour process in plunging pool of loose bed material[J].Journal of Hydraulic Engineering,2001,127(3): 219-229.
[9] 刘安富,杨敏,李会平,等.宽尾墩消力池透水底板脉动压力试验研究[J].水科学进展,2012,23(2): 243-248.(LIU Anfu,YANG Min,LI Huiping,et al.Experimental study of the fluctuating pressure on pervious slab in stilling basin under jet flow from tail-flaring piers[J].Advances in Water Science,2012,23(2): 243-248.(in Chinese))
[10] 辜晋德,彭秀芳.消力池底板缝隙水流脉动压力频谱分析研究[J].水力发电学报,2013,32(6): 177-182.(GU Jinde,PENG Xiufang.Study on spectrum of fluctuating pressure under bottom slabs of stilling basins[J].Journal of Hydroelectric Engineering,2013,32(6): 177-182.(in Chinese))
[11] ANNANDALE G W.Erodbility[J].Journal of Hydraulic Research,1995,33(4): 471-494.
[12] 潘别桐,井兰如.岩体结构概率模拟和应用[M].沈阳: 东北工学院出版社,1989: 1-79.
[13] 陈剑平.岩体随机不连续面三维网络数值模拟技术[J].岩土工程学报,2001,23(4): 397-402.(CHEN Jianping.3D network numerical modeling technique for random discontinuities of rock mass[J].Chinese Journal of Geotechnical Engineering,2001,23(4): 397-402.(in Chinese))
[14] 刘晓丽,王恩志,王思敬,等.裂隙岩体表征方法及岩体水力学特性研究[J].岩石力学与工程学报,2008,27(9): 1814-1821.(LIU Xiaoli,WANG Enzhi,WANG Sijing,et al.Representation method of fractured rock mass and its hydraulic properties study[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(9): 1814-1821.(in Chinese))
[15] 刘晓丽, 王恩志, 王思敬.裂隙岩体精细结构描述及工程特性数值试验[J].岩石力学与工程学报, 2008, 27(增刊2): 3935-3940.(LIU Xiaoli, WANG Enzhi, WANG Sijing.Fine structure description for fractured rock mass and numerical tests on its engineering properties [J].Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Sup2): 3935-3940.(in Chinese))[16] 束龙仓,张春艳, 闵星,等.不同隙宽条件下L形裂隙水头损失试验[J].河海大学学报:自然科学版,2013,41(5):383-388.(SHU Longcang,ZHANG Chunyan,MIN Xing,et al.Experimental study on water head loss of L-shaped fractures with different aperture widths[J].Journal of Hohai University:Natural Sciences,2013,41(5):383-388. (in Chinese))
Numerical simulation on propagation of fluctuating pressure of flow within rock fractures//
LI Aihua, ZHU Jiang
(SchoolofPetroleumEngineering,ChinaUniversityofPetroleum,Qingdao266580,China)
We used the Monte-Carlo method to analyze the influence of network structure on the propagation law of fluctuating pressure of flow within fractures. A replica of the fracture network was created by numerical simulation, which has resembled statistical characteristics with natural fracture network. Taking the replica of fracture network as main space of fissure water, a one-dimensional transient flow model was established to numerically simulate the propagation of fluctuating pressure. And then, the unsteady time process of fluctuating pressure’s propagation of fissure water and the spatial distribution nephogram of fluctuating intensity were generated. We concluded that the propagation of fluctuating pressure in rock fracture network has significant anisotropy. And the transient fluctuating pressure at any node within fractures is determined by the combination of three factors: the hydro-transient effect of fracture line elements connected with the node(especially of those directly connected with the node), the interfering source at fracture entrances, and the reflection source at fracture ends.
fluctuating pressure; fracture network; Monte-Carlo method; transient flow model; numerical simulation
中央高校基本科研业务费专项(12CX04024A,13CX02049A)
李爱华(1978—),女,山西祁县人,副教授,博士,主要从事流体力学及计算流体力学研究。E-mail: aiwali0524@163.com
10.3880/j.issn.1006-7647.2015.04.006
P641.2
A
1006-7647(2015)04-0024-04
2014-04-18 编辑:郑孝宇)
