冰体力学本构模型的构建
2015-08-28孟闻远郭颍奎
孟闻远,郭颍奎
(华北水利水电大学土木与交通学院,河南 郑州 450011)
冰体力学本构模型的构建
孟闻远,郭颍奎
(华北水利水电大学土木与交通学院,河南 郑州 450011)
为建立不同条件(温度、加载速率、围压)下冰的力学本构模型,采用理论分析和试验研究相结合的方法,通过比较冰的单轴压缩试验和比例加载条件下三轴压缩试验的应力-应变曲线特征,确定选用幂强化力学本构模型来描述冰体受力时的应力-应变关系;根据三轴压缩试验数据,采用最小二乘法曲线拟合,建立了两种试验条件下冰的力学本构模型;误差分析结果表明,所建立的冰体力学本构模型是比较准确的。
冰;力学本构模型;模型构建;三轴压缩试验;最小二乘法;曲线拟合
目前,国内外开展的冰体力学试验研究较少,我国近几年一些单位相继建立了冰力学试验室,还装备了大比例模型试验的冰容器和冰池[1-2],但在冰体力学性能、计算理论以及防凌减灾技术措施等方面仍无太多成熟的成果。冰体爆破三向受力的状态是客观的,而目前研究仍在单向受力试验的状态下进行[3-6],不能真实反映冰体受力状态与物理性能,冰的三轴力学试验国内目前还是空白。随着全球气候变化异常和沿河两岸经济建设发展,黄河、黑龙江等流域受凌汛危害影响越来越严重[7],为有效解决冰凌灾害的影响,开展有关冰的三轴压缩力学试验、构建冰的力学本构模型尤为重要。本文在冰体单轴压缩试验和比例加载条件下三轴压缩试验的基础上,建立了围压1.5 MPa、加载速率0.1 mm/min,温度分别为-5℃和-10℃两种试验条件下冰的力学本构模型,可为冰凌灾害防治研究提供一定的理论依据。
1 冰的力学试验
为建立冰的力学本构模型,本研究前期开展了冰的单轴压缩力学试验和三轴压缩力学试验。
1.1 冰的单轴压缩力学试验
参照有关材料力学性能试验标准[8],冰的单轴压缩力学试验采用人工制作的50 mm×100 mm圆柱体试件,所用设备和工具主要有低温冰柜、不锈钢管、塑料桶、切割机和钢锯等,需经过冷冻、取样、切割和加工等多道程序,试验所用仪器为微机控制电液伺服万能试验机,主要测试抗压特征,试验得到的典型应力-应变曲线如图1所示。
1.2 冰的三轴压缩力学试验
冰的三轴压缩力学试验采用50 mm×100 mm圆柱体冰试件,试验仪器为微机伺服高低温三轴试验机。为了获取三轴加载下的应力-应变曲线,通过比例加载,得到较为典型的冰的应力-应变曲线如图2所示。
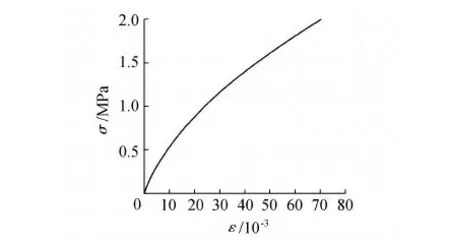
图1 单轴压缩试验冰的应力-应变曲线

图2 比例加载条件下三轴压缩试验冰的应力-应变曲线
通过三轴压缩试验,得到-5℃和-10℃两种试验条件下、不同时刻冰的应力σ和应变ε数据,具体可参见表1和表2。
2 冰体力学本构模型的构建
2.1 冰体力学本构模型的选择
对于不同的材料和不同的应用领域,可以采用不同的变形体模型。力学本构模型的选择必须符合材料的实际情况,以反映结构或构件中的真实应力及应变状态。此外,选择的力学本构模型数学表达式应足够简单,以方便具体问题的数学求解。常用的简化力学本构模型有理想弹塑性力学模型、线性强化弹塑性力学模型、幂强化力学模型和理想刚塑性力学模型[9-10]。
图1和图2试验结果表明,冰的单轴压缩力学试验应力-应变曲线(图1)和比例加载条件下三轴压缩应力-应变曲线(图2)均符合幂强化力学模型特征(图3),且三轴压缩试验与单轴压缩试验的应力-应变曲线有较好的形态拟合性,这也证实了“单一曲线假设”的正确性,由此推定冰材料采用幂强化力学模型具有合理性。

图3 幂强化力学模型应力-应变曲线
由于冰体强度较小,从受力到破坏一直应是主动加载、主动变形的过程,没有卸载的过程,同时,冰体的脆性、低强度特点,决定了整个破坏过程也是在小变形范围,因此冰材料本构模型采用幂强化力学模型是理想的,可方便计算。
幂强化力学模型可以避免解析式在ε=εs(达到屈服应变)处的变化,本文根据三轴压缩试验结果进行拟合,即取
(1)
其中
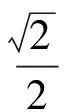
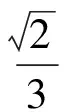
式中:s1、s2、s3为应力偏量分量;e1、e2、e3为应变偏量分量;m为幂强化系数(见图3),介于0与1之间,曲线在ε=0处与σ轴相切,且有
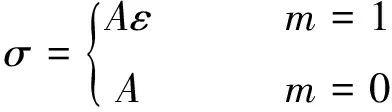
(2)
m=1代表理想弹性模型,若将式中的A用弹性模量E代替,则为胡克定律的表达式;m=0时,若将A用σs代替,则为理想塑性(或称刚塑性)力学模型。由式(2)可知,这两条线在ε=1处相交。式(1)中幂强化系数m可以在较大范围内变化,解析式比较简单,所以式(1)常被采用。
2.2 最小二乘法曲线拟合
冰体力学本构模型采用最小二乘法拟合,令拟合直线方程为
Y=a0+a1X
(3)
式中a0、a1是任意实数。应用最小二乘法原理,将实测值Yi与计算值的离差的平方和最小作为优化判据,通过求导,得到的两个以a0、a1为未知数的方程:
(4)

(5)
将式(4)(5)代入式(3), 即得到回归线性方程[11-12],也就是本文的数学模型。
2.3 冰体力学本构模型的建立及误差分析
2.3.1 力学本构模型的建立
为便于拟合,对式(1)两边取对数将该函数线性化,即
lgσ=lgA+mlgε
(6)
令lgσ=Yi、a0=lgA、a1=m、Xi=lgε,则有
Yi=a0+a1Xi
(7)
对于a0和a1,采用最小二乘法计算。
根据三轴压缩试验测得的数据(σ和ε),由lgσ=Yi、Xi=lgε,可得到-5℃和-10℃两种试验条件下的相关数据如表1和表2所示。
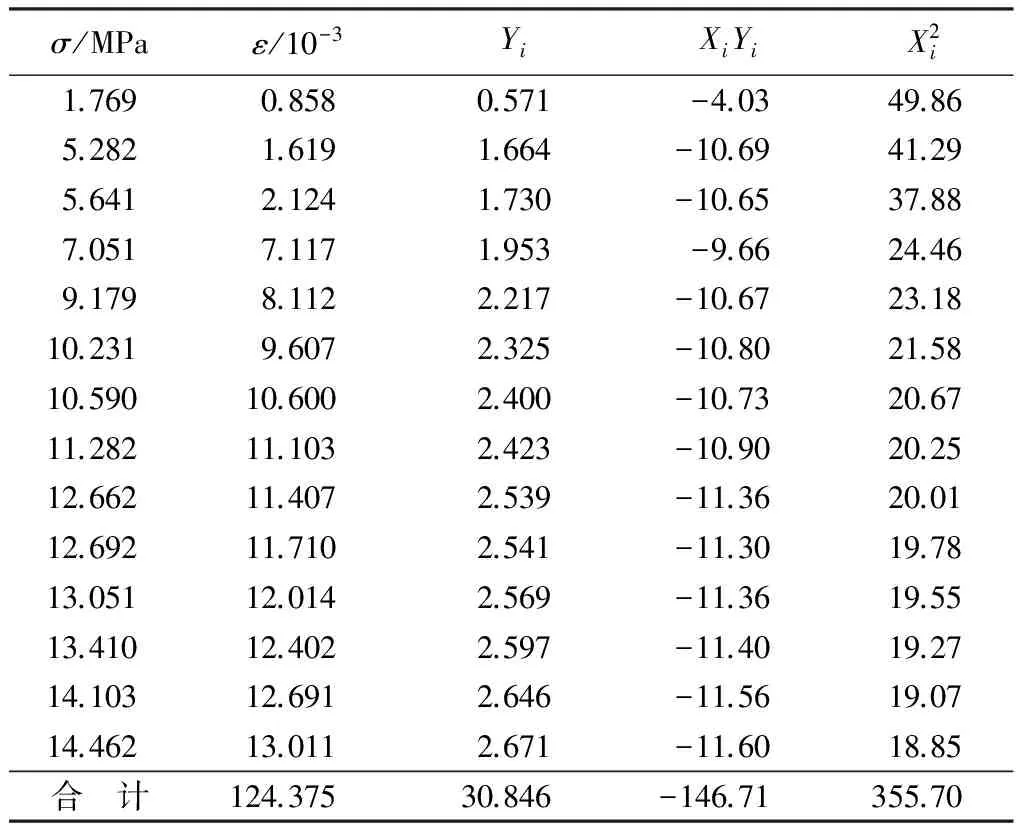
表1 -5℃试验条件下三轴压缩试验数据

表2 -10℃试验条件下三轴压缩试验数据
根据表1和表2,由式(4)和式(5)可求出a0和a1,再根据a0=lgA、a1=m可得到A和m,对于-5℃试验条件下的三轴压缩试验,可计算得a0=5.225,a1=0.609,A=185.9,m=0.609;对于-10℃试验条件下的三轴压缩试验,可计算得a0=5.262,a1=0.528,A=192.8,m=0.528,即两种试验条件下冰的应力-应变关系分别为
σ=185.9ε0.609
(8)
σ=192.8ε0.528
(9)
利用MATLAB软件,可将式(8)(9)拟合成曲线如图4所示。
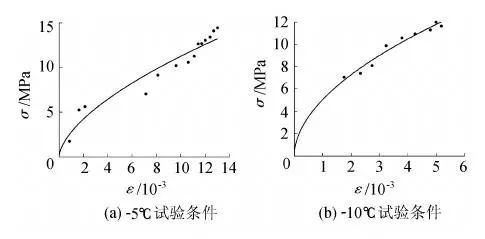
图4 三轴压缩试验冰的力学模型曲线
2.3.2 误差分析
拟合优度[12-13]是指回归直线对观测值的拟合程度,显然若观测点离回归直线近,则拟合程度好;反之则拟合程度差。度量拟合优度的统计量是可决系数(亦称确定系数R2):

(10)

由式(10)可知,R2的取值范围是[0,1],R2的值越接近1,说明回归直线对观测值的拟合程度越好;反之,R2的值越接近0,说明回归直线对观测值的拟合程度越差。 由式(10)可计算得本试验两种条件下,式(8)和式(9)的拟合优度分别为0.900 2和0.955 4, 可见两种试验条件下冰体力学本构模型拟合都非常理想。
3 结 论
a. 相对于单轴压缩试验,本文三轴压缩试验测得的冰体力学参数更接近实际,更加准确。
b. 冰体力学本构模型符合幂强化力学本构模型特征。
c. 拟合曲线(图4)符合幂强化力学模型的特点,证明了所选力学本构模型的正确性。
[1] 王金峰.河冰力学性能及其对桥墩撞击力的研究[D].哈尔滨:东北林业大学,2007.
[2] 宋安,汪震宇,史庆增,等.冰模拟实验与水利工程[J].水利水电技术,2005,36(7):140-143.(SONG An,WANG Zhenyu,SHI Qingzeng, et al. Ice model test and hydraulic engineering[J].Water Resources and Hydropower Engineering, 2005,36(7):140-143. (in Chinese))[3] 王金峰,于天来,黄美兰.河冰单轴无侧限抗压强度的试验研究[J].低温建筑技术,2007(1):11-13.(WANG Jinfeng,YU Tianlai,HUANG Meilan.The experimental research of the uniaxial unconfined compressive strength of River ice[J]. Low Temperature Architecture Technology, 2007(1):11-13. (in Chinese))
[4] 孙伟国.关于冰的抗压强度标准值的讨论[J].低温建筑技术,2009,31(5):19-20.(SUN Weiguo.The discussion of the compressive strength standard values of ice[J].Low Temperature Architecture Technology, 2009,31(5):19-20. (in Chinese))
[5] 于天来,张元,雷俊卿,等.春季流冰对桥墩产生动冰压力时冰抗压强度取值探讨[J].中外公路,2010,30(3):168-171.(YU Tianlai,Zhang Yuan,Lei Junqing, et al.The discussion of the compressive strength values with the dynamic ice pressure to the bridge pier of the spring ice[J]. Journal of China and Foreign Highway, 2010,30(3):168-171. (in Chinese))
[6] 罗天一,宋轶充,张丽敏,等.人工淡水冰的单轴压缩强度试验技术[J].工程与试验,2008,48(4):24-26.(LUO Tianyi,SONG Yichong,ZHANG Li, et al. The technology of the uniaxial compression strength test of the artificial freshwater ice[J].Engineering and Test, 2008,48(4):24-26. (in Chinese))
[7] 赵惠新, 戴长雷.国内冰凌研究现状综述[M].黑龙江:黑龙江大学出版社,2009.
[8] GB/T 50081—2002 普通混凝土力学性能试验方法标准[S].
[9] 徐秉业,刘信声.应用弹塑性力学 [M].北京:清华大学出版社,1995.
[10] 卓卫东.应用弹塑性力学[M].北京:科学出版社,2013.
[11] 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2001.
[12] 胡良平,高辉.非线性回归分析与SAS智能[M].北京:电子工业出版社,2013.
[13] 杨振海, 程维虎, 张军舰.拟合优度检验[M].北京:科学出版社,2011.
Construction of mechanics constitutive model of ice//
MENG Wenyuan, GUO Yingkui
(SchoolofCivilEngineeringandCommunication,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450011,China)
In order to establish the mechanics constitutive models of ice in different conditions (i.e., temperature, loading rate, and confining pressure), through the theoretical analysis and experimental research, we compared the characteristics of ice stress-strain curve in uniaxial compression test and triaxial compression test under proportional loading condition. Then, we described the relationship between stress and strain of ice by adopting the mechanics constitutive model of power hardening. Moreover, according to the data from the triaxial compression tests, we established the mechanics constitutive models in the two test conditions by using least squares curve fitting. Overall, the error analysis showed that the mechanics constitutive model of ice is comparatively accurate.
ice; mechanics constitutive model; model building; triaxial compression test; least squares; curve fitting
水利部公益性行业科研专项(201201080)
10.3880/j.issn.1006-7647.2015.04.008
O34
A
1006-7647(2015)04-0032-03
2014-09-15 编辑:熊水斌)
作者介绍:孟闻远(1965—),男,河南漯河人,教授,博士,主要从事土木工程、数值计算新方法等研究。E-mail:mwy@ncwu.edu.cn
