T-S 模糊系统量化H∞滤波器设计

赵 迪， 常晓恒

（1. 渤海大学 数理学院， 辽宁 锦州 121003； 2. 渤海大学 工学院， 辽宁 锦州 121003）

自1985 年Takagi 和Sugeno[1]提出了著名的T-S 模糊系统模型来描述复杂的非线性系统以来，T-S 模糊模型作为处理非线性系统的有效手段吸引了众多学者的关注[1-4]。 针对T-S 模糊系统的研究主要从T-S 模糊系统的稳定性分析和控制器、滤波器的设计两方面展开。 而状态估计作为控制领域的一个基本问题，模糊系统的状态估计也得到了广泛的研究，尤其是基于H∞滤波理论的T-S 模糊系统状态估计[2-4]。另一方面，伴随着数控时代的到来和网络化控制的兴起，反馈控制系统中存在的量化现象作为一个不可回避的问题也受到了广泛的关注[8-10]。 这是因为在传统的控制器、滤波器的没有考虑量化的影响，而量化现象又是普遍存在的，这就导致了当系统量化发生时，系统性能下降甚至不稳定。 其实有关于量化问题的研究最早可以追溯的1956 年，卡尔曼[8]指出了一个可稳定的量化控制器可能导致闭环系统出现极限环和混沌现象。 基于此，许多学者展开了对量化问题的研究从最早的理解和克服量化的影响到现在把量化器看作是信息编码器，提出了许多重要的成果[9-10]。

本文考虑了存在量化现象的离散T-S 模糊系统的状态估计问题， 主要是基于H∞滤波理论给出一套比现有方法保守性更低可行的滤波器设计算法使得T-S 模糊系统存在量化时达到渐进稳定并满足给定的H∞性能指标。

1 问题描述

考虑以下离散T-S 模糊模型，其第i 条模糊规则为

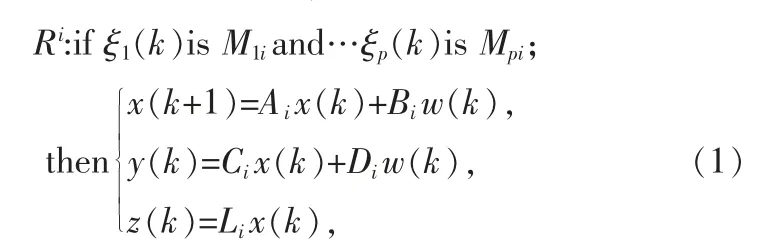
其中x（k）∈Rn为状态变量；y（k）∈Rf为测量输出信号；z（k）∈Rq为被估计信号；w（k）∈Rv为噪声信号且能量有界即w（k）∈l2（0，∞），ξ1（k），ξ2（k），…ξp（k）为可测量的前提变量，Mdi，d=1，2，…p，i=1，2，…r 是模糊集，r 为模糊规则数目，Ai，Bi，Ci，Di，Li为适当维数的系统矩阵。是前提变量ξd（k）相对于模糊集合Mdi的隶属度且满足

T-S 模糊模型（1）可写为如下形式：

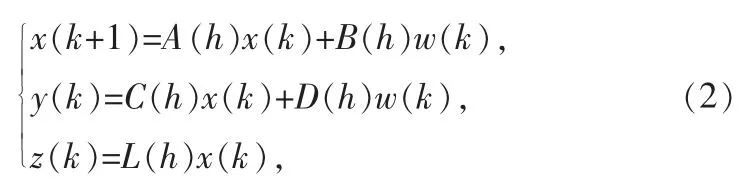
其中Λ（h）=hi（ξ（k））Λi，Λ=A，B，C，D，L。

考虑如下形式的全阶模糊滤波器：

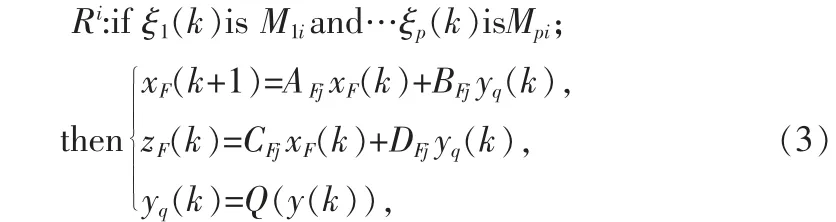
其中xF（k）∈Rn，yq（k）∈Rf，zF（k）∈Rq分别是滤波器的状态、输入和输出，AFj，BFj，CFj，DFj，j=1，2，…r 为需要设计的适当维数的矩阵。其中函数Q（·）表示对数量化器。本文考虑采用静态时不变对数量化器。 即Q（·）=[Q1（·），Q2（·）…Qf（·）]T并且满足Q（－V）=-Q（V）。根据Fu 等人定义[13]，对于（3），可以得到对于任意y（k）∈Rf有|Q（y（k））－y（k）|≤δy（k），δ=diag（δ1，δ2，…，δf）。 因此，yq（k）=Q（y（k））=（I+Δ（k））y（k），|Δ（k）|=diag（Δ1（k），Δ2（k），…，Δf（k））。 量化现象时，对于系统（2），其输出信号y（k）传送到滤波器时应变为Q（y（k））。

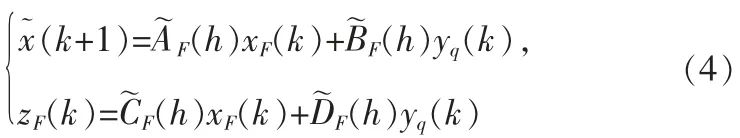
至此我们的目的可以阐述为针对上述存在输出量化现象T－S 模糊系统，设计滤波器（3）使系统在消除量化误差的影响同时，满足R1）和R2）。

R1）当w（k）=0 时，滤波误差系统（4）稳定。

R2）在零初始条件下即x~（k）=0，对于任意w（k）∈l2（0，∞），滤波误差系统（4）都能够满足给定的H∞噪声裕度γ，即‖e（k）‖2＜γ‖w（k）‖2。

下面的引理在后续研究中起关键作用。

引理1[6].给定矩阵Θ=ΘT∈Rn×n，和N∈Rn×n，不等式vTΘv＜0，∀v∈Rn，Nv=0，v≠0 成立，如果存在矩阵L∈Rn×n，满足Θ+LN+NTLT＜0。

引理2[5].给定矩阵Γ，Λ，和对称矩阵Ω，对于FTF≤I，不等式Ω+εΓFΛ+ΛTFTΓ＜0 成立， 只要存在一个恒定的标量ε＞0，满足Ω+ε－1ΓΓT+εΛTΛ＜0。

2 系统H∞性能分析

定理1:滤波误差系统（4）在满足给定的H∞指标γ 的前提下稳定，如果存在矩阵P+（h）＞0，P（h）＞0，N（h），M（h），X1（h），X2（h），X3（h），E，F，G 满足下面的矩阵不等式：

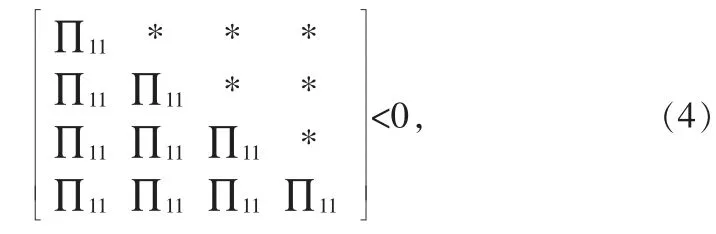
其中，

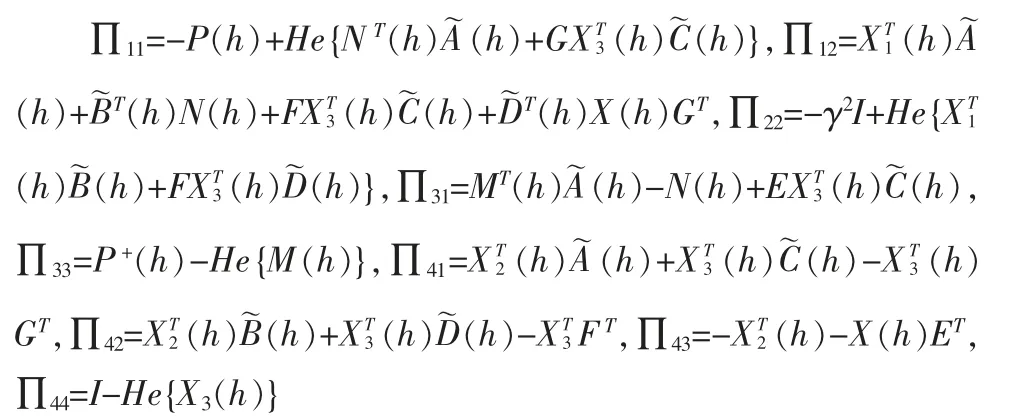
证明：构造如下模糊Lyapunov 函数：

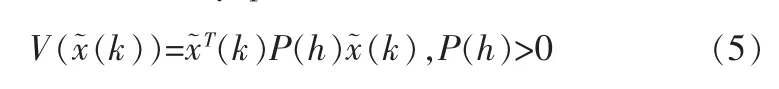
其差分为

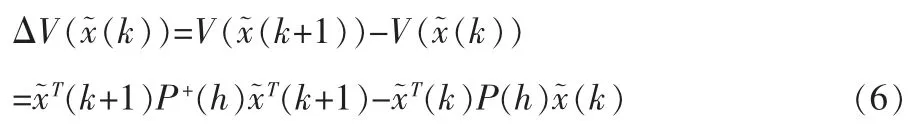
进而可得

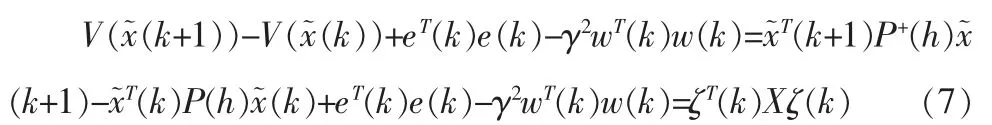
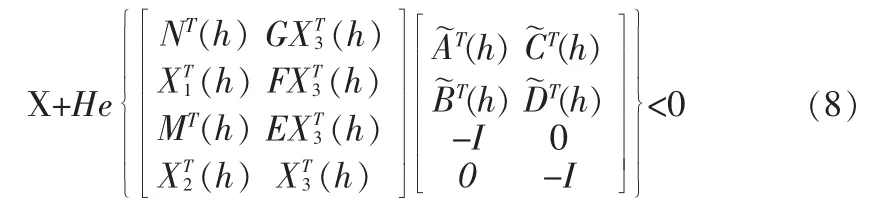
注1：我们推广Chang[4]中的方法来处理T－S 模糊系统H∞量化滤波问题，注意到当定理1 中E（h）=F（h）=G（h）=0 时，定理1 的结论降级为推广Chang[4]中所得的结果，由此可得对于T－S 模糊系统量化H∞滤波问题定理1 的设计条件比Chang[4]中的方法理论上保守性更低。 定理1 没有考虑量化误差的影响。 接下来，我们将给出充分条件来消除量化误差的影响。

定理2：假设系统和滤波器已给出，则滤波误差系统（3）在满足H∞范数指标γ 的情况下达到一致稳定当且仅当存在P+（h）＞0，P（h）＞0，N（h），M（h），X1（h），X2（h），X3（h），E，F，G 以及标量ε＞0 满足下面的矩阵不等式：

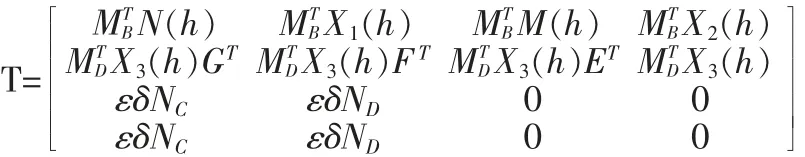
并且Φij为（4）中的∏ij用代替（4）中的所得。

证明：假设定理1 中的条件是满足的。 我们把（3）中的定义带入定理1 的结论，则（4）可写为如下形式：

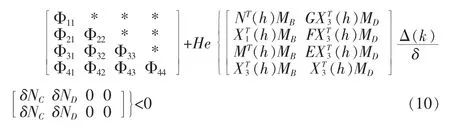
其中，MB=[0，MD=－DF（h），[C（h），0]，ND=－D（h）则对（10）应用引理2 可得（10）成立当且仅当存在一个标量ε＞0，满足：

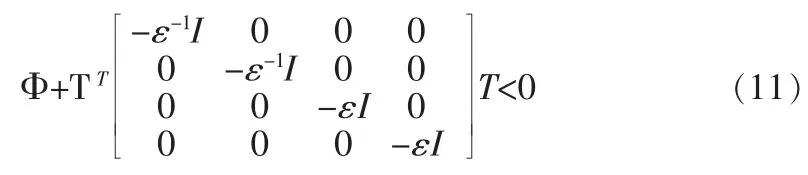
对（11）应 用Schur 补，最 后 再 调 用diag（I，I，I，I，I，I，εI，εI）执行同余变化，则可得定理2 的结论。

基于定理2，我们将给出线性化过程来设计H∞滤波器。

3 H∞滤波器设计

定理3:给定量化密度ρ＞0，对于离散T－S 模糊系统，存在滤波器能够消除量化误差并且能够保证滤波误差系统在满足给定H∞裕度γ 的前提下渐进稳定的条件是，存在矩阵P1i，P2i，P3i，P1l，P2l，P3l，N1j，N2j，M1j，M2j，X1j，X2j，i，j，l=1，2，…，r，G，E，F 和非奇异矩阵N3，X 以及标量λ1，λ2，λ3，λ4，λ5，ε＞0 满足下面的线性矩阵不等式：

对于i，j，l∈（1，r），其中

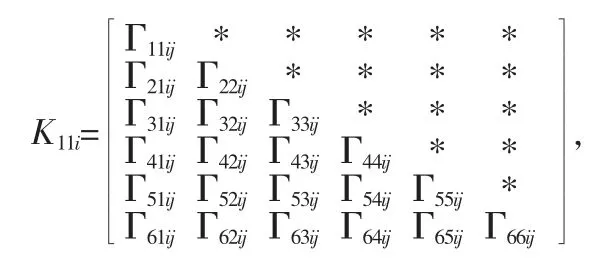
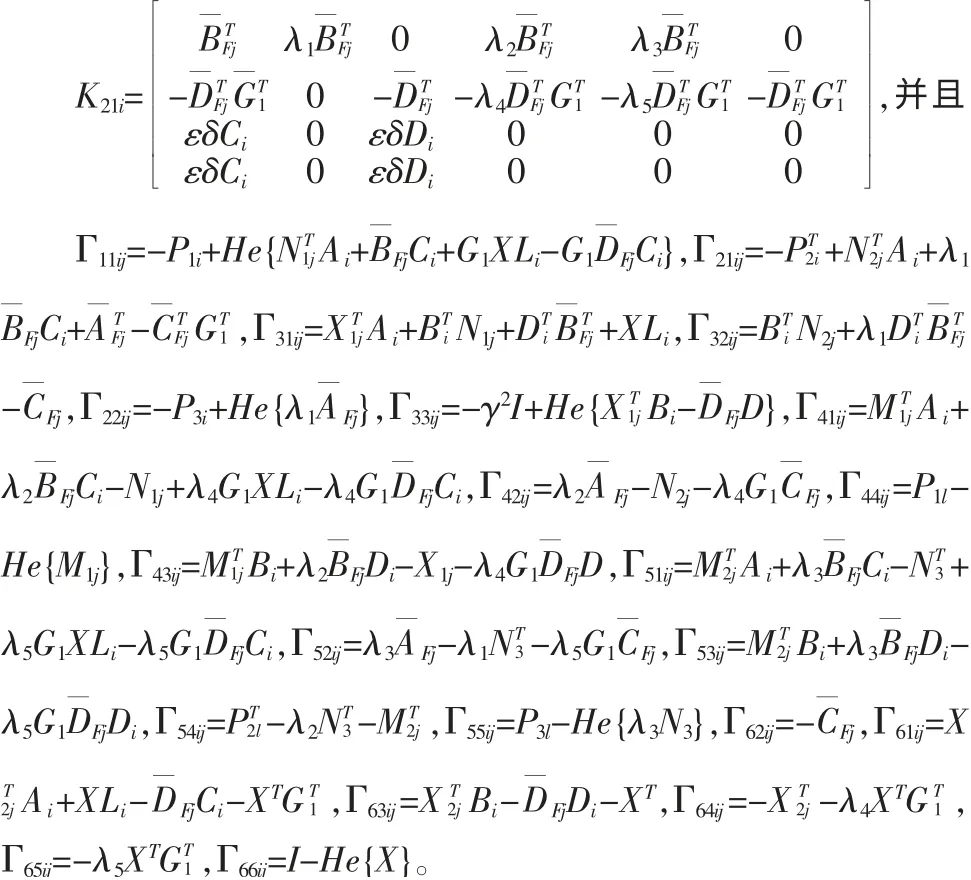
由此， 可以得到一个满足给定H∞性能指标γ＞0 的合适滤波器：

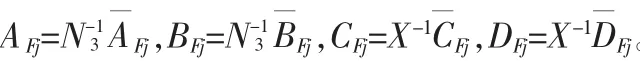
证明：如果定理2 中不等式成立，我们便可以设计滤波器，这里假设在（9）中涉及到的矩阵变量具有如下的形式并且定义：，

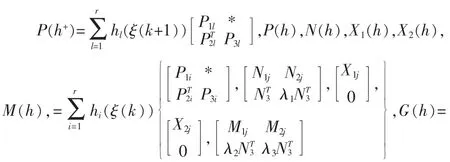
注2： 通过对定理2 上面的相关矩阵做上述结构上的定义， 可以使得原先在定理2 的不等式中出现的那些耦合项很好的分开了。另一方面，为了降低这样对矩阵变量结构上定义带来的保守性， 文中引入了几个补偿参变量λl，l=1，2，3，4，4和G1来获得解空间中额外的自由度。 这些变量可以利用Chang[7]中提到的方法得到。

注3：在实际的应用中，量化误差的上限δ 可以根据给定的量化密度ρ 计算得到。 因此， 定理3 中的不等式组 （12）－（13） 实际上是严格的线性矩阵不等式 （LMIs）， 故可以通过MATLAB 的控制工具箱来求解从而设计滤波器。

4 仿真分析

本节我们将通过实例验证之前论述的方法的有效性。 考虑隧道二极管电路，其T－S 模糊模型如[5，7]所描述其中，

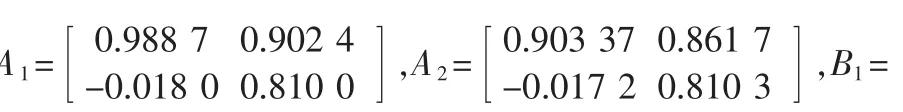
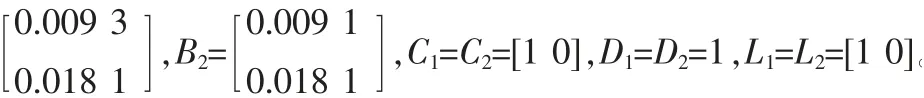
我们给定（13）中的优化参数如下λl=-0.15，l=1，2，3，λl=我们用定理3 中的方法来处理T-S 模糊系统H∞量化滤波问题，得到相应的γmin为1.3408。 对应定理3求得的滤波器参数矩阵如下：

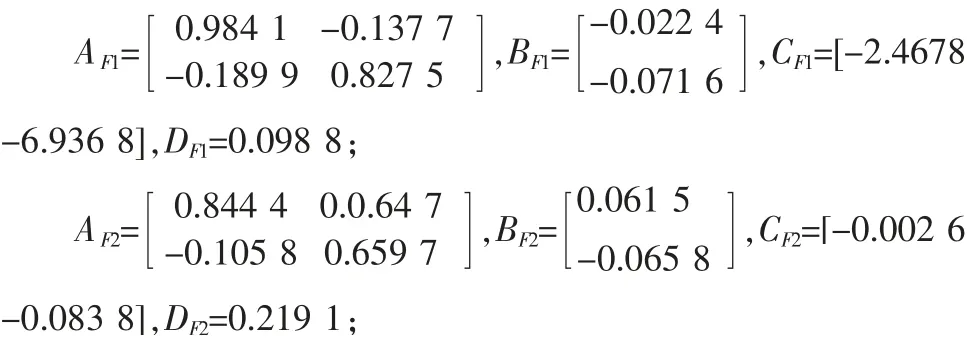
5 结 论

文中解决了离散T-S 模糊系统的量化滤波问题， 采用模糊Lyapunov 函数方法和松弛变量的引进，给出了基于LMI 技术一种量化H∞滤波器设计的充分条件。理论证明显示了所提方法的优越性，最后通过仿真实例验证该方法的有效性。

[1] Takagi T，Sugeno M. Fuzzy identification of systems and its applications to modeling and control [J]. Systems， Man and Cybernetics， IEEE Transactions on，1985（1）:116-132.

[2] Gao H，Zhao Y，Lam J，et al. Fuzzy filtering of nonlinear systems with intermittent measurements[J]. Fuzzy Systems，IEEE Transactions on，2009，17（2）:291-300.

[3] Zhou S，Lam J，Xue A. H∞filtering of discrete-time fuzzy systems via basis-dependent lyapunov function approach[J].Fuzzy Sets and Systems，2007，158（2）:180-193.

[4] Chang X H，Yang G H. Non-fragile H∞filter design for discrete-time fuzzy systems with multiplicative gain variations[J].Information Sciences，2014，266:171-185.

[5] Petersen I R. A stabilization algorithm for a class of uncertain linear system[J]. Systems & Control Letters，1997，8（4）:351-357.

[6] Skelton R E，Iwasaki T，Grigoriadis K. A unified approach to linear control design[M]. CRC Press，1997.

[7] Chang X，Yang G. Robust H-infinity filtering for uncertain discrete-time systems using parameter-de pendent Lyapunov functions [J]. Journal of Control Theory and Applications，2013，11（1）:122-127.

[8] Kalman R E. Nonlinear aspects of sampled-data control systems[C]//Proc. Symp. Nonlinear Circuit Analysis VI. 1956:273-313.

[9] Fu M，Xie L. The sector bound approach to quantized feedback control [J]. Automatic Control， IEEE Transactions on，2005，50（11）:1698-1711.

[10]Gao H，Chen T. A new approach to quantized feedback control systems[J]. Automatica，2008，44（2）:534-542.