GIS局部放电小波阈值去噪算法的改进

陈 迅，秦海亭，刘 利，王黎明

（江苏科技大学 电子信息学院，江苏 镇江 212003）

局部放电是指在电场作用下，绝缘系统中只有部分区域发生放电而没有形成贯穿性放电的一种放电现象[1]，是由于生产过程中造成的缺陷或绝缘系统内部老化，在高电场强度作用下发生重复击穿和熄灭的现象。局部放电既是GIS绝缘劣化的征兆和表现形式，又是绝缘进一步劣化的原因。

电力设备局部放电检测技术的研究对于设备的在线监测具有重要的实际意义。局部放电会使电力设备绝缘系统加速老化，引起绝缘故障，缩短使用寿命，为确保变压器能够安全运行，需及时发现电力设备内部潜伏性的绝缘故障[2]。近年来众多学者在这方面做了深入的研究。由于局部放电的信号很微弱，而在实际设备运行的现场却往往存在大量的噪声干扰，严重影响了局部放电在线监测的灵敏度和精度，为了正确地分析局部放电信号，首先必须解决噪声干扰抑制的问题[3]。

1 小波阈值去噪

针对局部放电信号中的各种干扰，国内外的学者也提出了相应的抗干扰技术。近年来，随着对小波去噪算法的深入研究，小波去噪方法也丰富起来。目前比较常用的小波除噪方法有：模极大值去噪算法、相关性去噪算法和小波阈值去噪算法[4]。

其中，模极大值去噪算法不仅不需要估计噪声的方差，还能较好的分析信号的奇异性，从而保留信号的重要信息，可以将其应用到信号的去噪中[5]。考虑到小波函数模极大值受白噪声的影响较大，致使大尺度下的平滑作用使模极大值的定位产生的偏差，导致重构信号有一定的误差；同时，在小的尺度上如何更好的恢复1、2尺度的小波系数成为一个重要问题[6]。

而相关性去噪算法主要是根据信号和噪声在经小波分解后表现出不同的特性被提出和应用的，但在计算相关系数时，受到小波系数在时间轴上的影响各尺度间小波系数的偏移会降低判断的准确率[7]。小波阈值去噪算法实现简单，计算量小，因而应用最为广泛。常用的小波阈值去噪算法有硬阈值法、软阈值法以及相关的改进算法。

本文在此基础上提出了一种基于新的阈值函数的小波阈值去噪算法。其中，新阈值函数与原来的阈值函数相比，不仅表达式简单、易于计算，而且具有无穷阶导数，便于进行各种数学处理等诸多优良数学性能，同时很好地改善了硬、软阈值方法的去噪效果，发挥了阈值去噪的优越性。

最后用仿真试验验证了基于新的阈值函数的去噪算法在去噪方法中具有良好的效果。

对于任意函数 Ψ∈L2（R），如果满足“容许性”条件[8]：

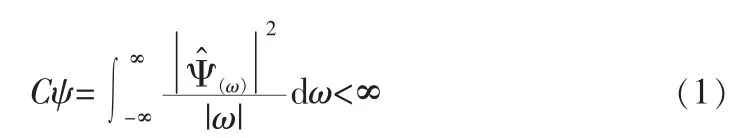
则Ψ可以作为一个“基小波”。进而，在L2（R）上的积分小波变换定义为：

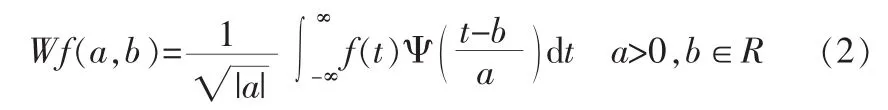
如果令 ψa，b）为尺度参数，b为平移参数，式（2）可写为：

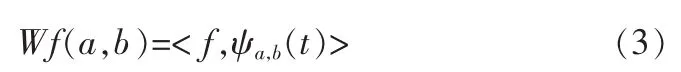
经小波变换后，在每个尺度上得到一组一维的小波系数。如果Ψ满足上述容许性条件，则其变换是可逆的，反变换为：

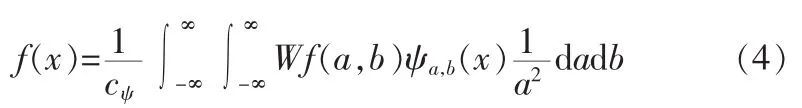
即根据信号的小波变换系数 可以精确的恢复原信号。

而在实际的应用中，为了便于计算机实现，需要将小波变换离散化。仿照傅里叶变换和傅里叶级数的关系，希望小波函数Ψ（x）经过伸缩和平移构成L2（R）的一组正交基：

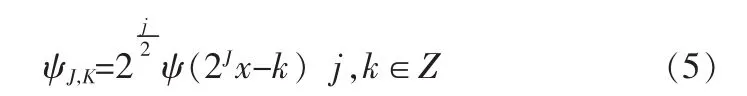
这样以来，任意函数f∈L2（R）都可以表示为小波级数的形式：

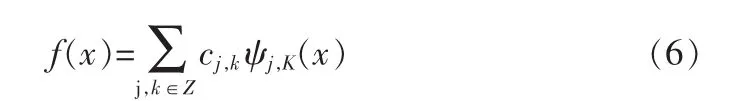
事实上，只要{Cj，k}满足 Riesz 条件：

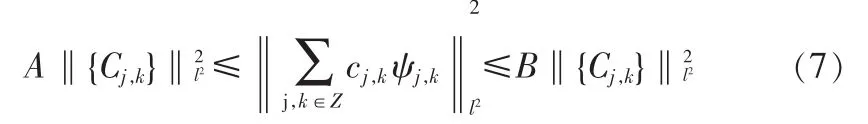
上述小波级数便成立，其中：

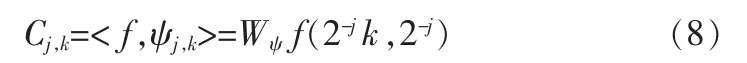
称为小波系数。 它实际上是小波变换在离散的点（2－jk，2－j）上的值，也就是离散的二进小波变换。如果ψj，k满足Riesz条件，离散的二进小波变换的逆变换是一个小波级数。

信号经过小波变换后，可以认为由信号产生的小波系数包含有信号的重要信息，其幅值较大，但数目较少，而噪声对应的小波系数幅值小。通过在不同尺度上选取合适的阈值，并将小于阈值的小波系数置零，而保留大于阈值的小波系数，从而使信号中的噪声得到有效的抑制，最后进行小波逆变换，得到滤波后的重构信号。小波阀值去噪的流程如下：

含噪信号→小波变换→硬/软阈值处理→小波重构→去噪后信号

其中硬阀值去噪算法的计算步骤如下：

对待降噪信号3求小波变换，得到一系列小波系数{cj，k}；

除了最粗尺度信号外，将每个尺度j上的小波系数进行阈值处理，阈值取为：

其中，σ为噪声的标准差，Nj为该尺度上小波系数的个数。当某小波系数大于阈值时，保留原值，否则置零，用公式表示为阈值函数：

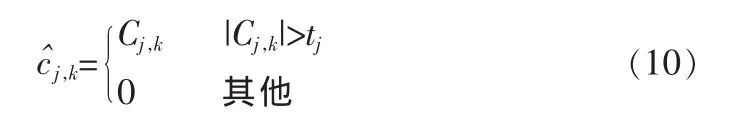
式中，tj为预置阈值，cj，k为小波分解系数，为估计的小波系数。

利用阈值处理后的小波系数{cj，k}做小波逆变换，重构信号，便可得到去噪后的信号。

与硬阈值相对，软阈值算法只是阈值函数不同，其他步骤均相同。当某小波系数大于阀值时，向着减小系数幅值的方向作一个收缩t，否则置零，用公式表示为阈值函数：

由此可见，小波阈值滤波算法的两个关键问题是阈值（或噪声标准差σ的估计）与阈值函数的选取。

2 改进的阈值函数

硬、软阈值算法虽然在实际中得到了广泛的应用，也取得了较好的效果，由小波阈值去噪公式可知，软阈值是对硬阈值的扩展，但这些算法本身还存在一些缺陷，在一般情况下，用硬阈值处理过的信号要比用软阈值处理后的信号粗糙，这是因为硬阈值法往往使得滤波结果具有较大的方差 （主要因为滤波后的不连续性），因此在硬阈值处理过程中，利用cj，k重构所得的信号可能会产生一些振荡。而采用软阀值处理方法虽然可以获得比较平滑的去噪信号，且软阀值方法中估计小波系数有着良好的连续性，但由于当小波系数较大时，c^j，k与cj，k之间总存在恒定的偏差，这将直接影响重构信号与真实信号的逼近程度，给重构信号带来不可避免的误差。从而使得软阈值法滤波结果具有较大的偏差 （主要因为对所有大于阈值的系数共同做了收缩）[8]。为了尽可能减少它们之间的偏差，构建了如下新的小波阈值函数：

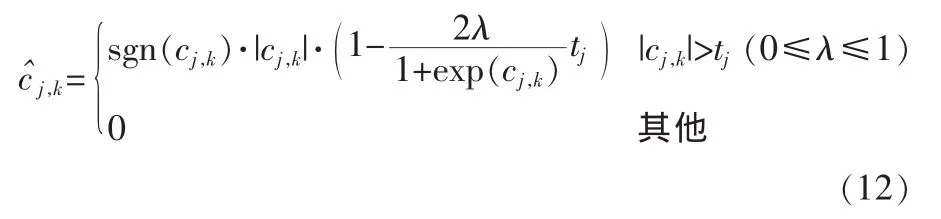
式（12）中，cj，k为被噪声污染后的小波分解系，为估计的小波系数，tj为阈值。

该方法思路简单、易于实现，且与前两者相比具有良好的效果。构建的新的阀值函数具有高阶导数，使得其在信号和噪声之间有着一个平滑的过渡区间。由于软阈值算法估计出来的小波系数c^j，k的绝对值总是比cj，k要小tj，从而影响了重构精度，所以需考虑减小此偏差，但这种偏差减小到零也不一定是最好的（硬阈值的情况）。因为多数情况下cj，k本身就是由uj，k（信号对应的小波系数）和 Vj，k（噪声对应的小波系数）组成的，而目的是使‖－uj，k‖最小，因此使的取值介于 cj，k－tj和 cj，k之间可能会使估计出来的小波系数更加接近于 uj，k，基于这一思想构建了该阈值函数。考察此函数：

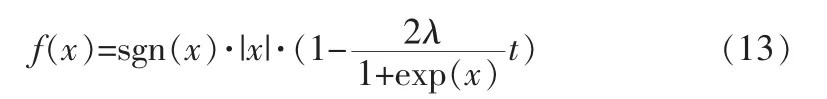
可知，当 λ 取 0 和 1 之间的数，x→±∞ 时，有 f（x）－x→2λt，即随着 cj，k的增大，和 cj，k的偏差的绝对值逐渐减小为2λt，所以大大减小了软阈值方法中产生的恒定偏差，从而提高了重构精度，改善了去噪效果。

可见相对于硬、软阈值函数，新阈值函数更优、更灵活，效果。如图1为硬阈值函数、软阈值函数以及改进阈值函数的曲线图。

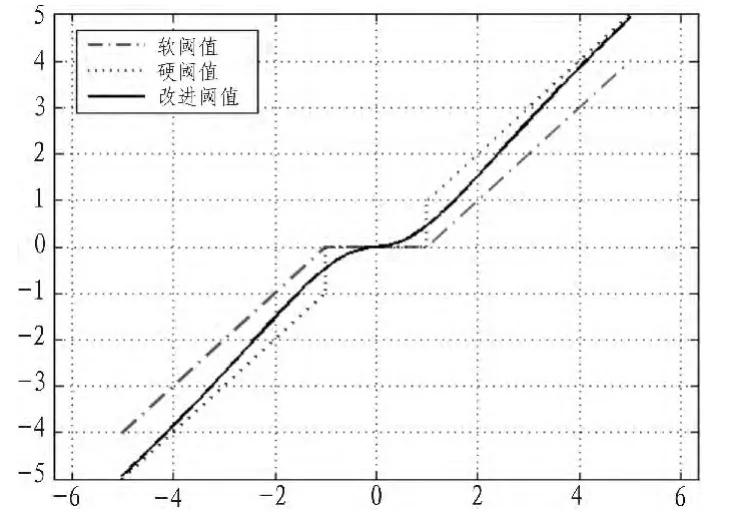
图1 3种阈值函数曲线图Fig.1 3 kinds of threshold function curves

3 仿真试验

为了说明新阈值函数在去噪算法中的有效性和优越性，分别采用传统的硬、软阈值函数和新阈值函数进行试验对比。文中应用MATLAB仿真软件对Bumps信号加入白噪声，然后分别采用硬阈值、软阈值和本文中提出的阈值去噪算法进行去噪，该信号采用了sym8小波对含噪信号进行3层小波分解，用最小极大方差法确定阈值。

图2为Bumps信号及其用硬阈值、软阈值和新阈值去噪算法进行去噪仿真的结果，从下图中可以看出，硬阈值和软阈值去噪均有不同程度的波形失真，而新的阈值去噪方法达到了较好的去噪效果。

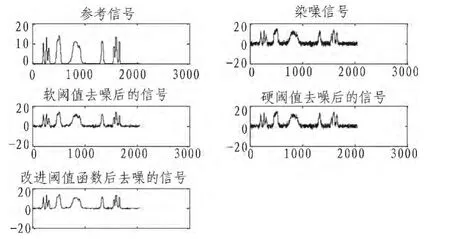
图2 Bumps信号去噪结果对比Fig.2 The denoising results compared to Bumps signal

下表列出了此3中方法对含噪的Bumps信号去噪后的信噪比和均方差，从表中可知，改进的小波去噪阈值方法信噪比最高，与硬阈值相比提高了23.74%，与软阈值相比提高了79.98%，而均方差最小，与硬阈值相比降低了60.43%，与软阈值相比降低了30%，所以去噪效果最好。

表1 Bumps信号的3种去噪结果比较Tab.1 Comparison of 3 kinds of Bumps signal denoising results

参照文献[9]提出的用数学模型来表示局部放电脉冲信号的方法，采用单指数衰减震荡模型来模拟局部放电信号，并对其进行仿真试验。有如下数学表达式：

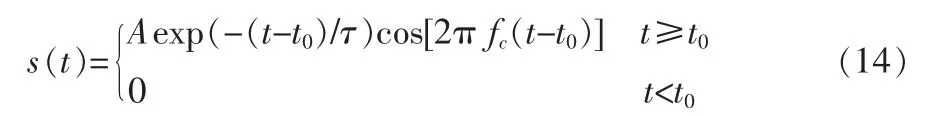
式中，A为信号的振幅，τ为信号衰减系数，t0为放电时刻，fc为放电信号主频率。 当选取 A=5 A，τ=2 μs，t0=10 μs，fc=1 MHz时，信号模拟放电波形如图3中的参考信号波形：

白噪声在这里服从均值m=0，方差σ2=1的高斯分布随机序列来模拟。本文选用db2小波对局放信号进行3层分解，当选取λ=0.8时，由仿真结果图3可以看出，软阈值去噪效果失真明显，改进后的阈值去噪效果相对于硬阈值去噪较为理想，而如何保持更高的稳定度是以后继续研究的一个方向。

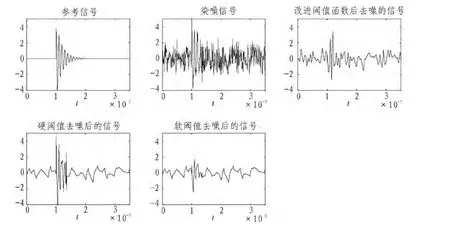
图3 局部放电仿真波形和信号去噪结果对比Fig.3 The waveform of PD simulation and the denoising results compared to the signal

4 结 论

文中提出了一种基于新的阈值函数的去噪算法，与传统的硬、软阈值去噪方法相比，去噪效果无论在信号输出波形上还是在去噪后信号的信噪比和均方误差意义上都有了明显改善，而且新阈值方法很灵活，且具有比较好的稳定性。去噪仿真的结果也说明了改进后的小波阈值去噪算法能够较好地完成对波形提取的工作，在GIS局部放电检测方面具有较好的工程应用价值。

[1]牛海清.高压直流局部放电的模糊识别及去噪策略[D].广州：华南理工大学，2009.

[2]藏怀刚，王志斌，郑英.改进小波阈值函数在局放去噪分析中的应用[J].自动化仪表，2010，31（5）:5-7.ZANG Huai-gang，WANG Zhi-bin，ZHENG Ying.Application of improved wavelet threshold function in partial discharge signal de-noising analysis[J].Automation Instrumentation，2010，31（5）:5-7.

[3]钱勇，黄成军，陈陈，等.多小波消噪算法在局部放电检测中的应用[J].中国电机工程学报，2007，27（6）:89-95.QIAN Yong，HUANG Cheng-jun，CHEN Chen，et al.Application of multi-wavelet based on denoising algorithm in partial discharge detection[J].Proceedings of the CSEE，2007，27（6）:89-95.

[4]华春红，任章，张敏虎.基于自适应阈值估计的模极大值去噪方法[J].航天控制，2011，29（1）:37-40.HUA Chun-hong，REN Zhang，ZHANG Min-hu.The wavelet maxima denoising based on the adaptive bayes shrink threshold[J].Aerospace Control，2011，29（1）:37-40.

[5]廖华.GIS局部放电在线监测系统及核主分量模式识别研究[D].重庆：重庆大学，2008.

[6]王瑞，张友纯.新阈值函数下的小波阈值去噪[J].计算机工程与应用，2013，49（15）:215-218.WANG Rui，ZHANG You-chun.New threshold function in wavelet threshold de-noising[J].Computer Engineering and Application，2013，49（15）:215-218.

[7]秦毅，王家序，毛永芳.基于软阈值和小波模极大值重的信号降噪[J].振动、测试与诊断，2011，31（5）:543-547.QIN Yi，WANG Jiang-xu，MAO Yong-fang.Signal denoising based on soft thresholding and reconstruction from yadic wavelet transform modulus axima[J].Journal of Vibration，Measurement，2011，31（5）:543-547.

[8]段大鹏.基于UHF方法的GIS局部放电检测与仿生模式识别[D].上海：上海交通大学，2009.

[9]艾比布勒-赛塔尔，徐文邦，王德平，等.局部放电小波阈值去噪算法的改进[J].电子测试，2014（10）:26-28.Aibibule-Saitaer，XU Wen-bang，WANG De-ping，et al.The improvement of wavelet threshold denoising algorithm of partial discharge[J].The Electronic Test，2014（10）:26-28.