基于Kinect 传感器的三维重建算法研究

李 秦， 夏选太

（1. 陕西财经职业技术学院 陕西 咸阳 712000； 2. 西安创联新能源设备有限公司 陕西 西安710065）

随着现代视觉技术的不断发展，三维重建技术开始被广泛的应用在各个行业和领域当中，改变着人们在生产、生活，如通过三维重建，可辅助分析病人病情，并模拟手术。 而作为美国微软公司生产的一部红外线深度摄像机，其可非常快速的获取相关的图像，并在三维重建方面具有非常低廉的成本和灵活性。 但是，传感器在对图像进行获取的时候，其精准度非常低，以此导致在捕捉的过程中失真，影响图片捕捉的效果。 对此，本文则结合自身的研究，提出一种基于特征点的配准算法，并对其实现进行深入分析。

1 三维重建技术的流程

所谓的三维重建是指通过采用计算机图形学、 人工智能、计算机技术、图像处理技术等，实现对物理三维模型的重建，以此方便对三维的信息进行识别和认知。 根据相关的经验总结，三维重建其一般的流程则如图1 所示。

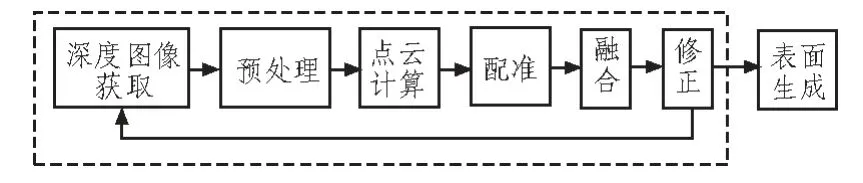
图1 三维重建流程Fig. 1 Three-dimensional reconstruction flow

通过图1 可以看出，在对图像进行获取之后，计算机则自动生成点云数据，并对其中的多帧点进行云配准之后，对图像进行融合，最终生成为相应的三维模型。 文中例举的重建流程则主要是借鉴和参照中设计的流程，主要包括图像深度获取、预处理、点云计算、配准、融合、修正、生成表面等阶段。

2 点云配准

通过采用不同视角的深度图像， 其可获得不同的点云。但是， 上述的点云其都是基于摄像机自身的坐标系而定的。因此，在对点云进行获取的过程中，需要进行不同的坐标变换，并将其中的各个不同的坐标系都全部统一到世界坐标系当中。 在对坐标进行变化求解相关变换参数的过程即被称为配准。 而在进行配准的时候，需借助当前帧和前一帧的相关的点云数据，并将前一点云作为变换的基础值，对其进行计算，最后得到相关的变化参数。

2.1 算 法

也被成为迭代对应点算法，其具体的过程作为：

输入待配准点P 和Q， 初始变换参数为Tini： 输出参数为T。 令Po=P，计数器k=0，通过采用一定的规则可找到离Q 和Pk之间最为近的那个点；计算目标函数的最小值，并得到其相应的Tk和与其对应的误差Ek；对点云进行更新；如其中的Tk满足一定的条件，如Ek满足收敛，则结束迭代，如不满足，则继续对其误差进行计算。 其中，目标函数误差的表达式为：

其中的E 表示为误差，T 为变换参数，Pi、Qi分别表示为相应的对应点的集合，N 为对应点的对数。

2.2 变换参数求解

在对算法进行迭代的过程中，通常则采用非线性的最小二乘法对其进行求解，但是，在点云进行查找的过程中，其中的两个点云其距离非常接近的时候，其可采用线性二乘法得出其相似的非线性最优解。 因此通过上述思路对分析，需要满足：

其中其平移向量t=（tx，ty，tz）T，而其中的旋转矩阵则为：

其中Rz（θ3）、Ry（θ2）、Rx（θ1）则分别表示其为绕着z 轴、y轴和x 轴进行旋转，其角度则分别为括号之中对应的角度。当两点在较为接近的时候，其中对应的角度则分别趋近于0。 由此可得到其旋转矩阵的近似值则为：

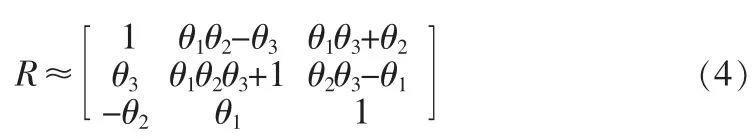
对此，各对应的运点到其相应的切平面的距离为：

由此，通过对公式（5）进行的矩阵运算可以构造出新的方程（构造过程省略）：

通过公式（6）对R、t 的求解，并结合奇异值分解法，可得到该运算的最终求解方程：

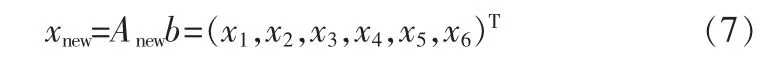
同时针对上述的问题分析， 可以得出如果采用手持的的移动速度慢，所以该方法是适用于求解变换参数。

3 基于Kincet 的三维重建配准算法

通过采用ICP 的算法，可实现对其变换参数的求解。而该算法其仅仅只考虑到了其中的两个不同云点的空间距离，与物体的运动状态没有任何的关系。 同时， 当前应用的主流的Kincet 的分辨率为640*480，通过图1 中的去除背景，则保留下的像素点的数量有限。 而此时如果采用传统的特征点的方法，则将给系统带来很大的误差，对此，文中提出在有限的数量之中，采用分类的方法对其进行改进，其具体的改进流程则如图2 所示。

图2 改进后的配准算法Fig. 2 Registration algorithm improved

该改进算法的原理则为首先对基于Kincet 的像素点进行去除背景，在此之后对剩下的点进行分类，最后再利用不同的目标误差函数进行配准， 而其中所谓的分为则为对图像当中前一帧和当前帧的云点进行分类，并在该步骤的基础之上，根据其中云点的不同而选择不同的目标误差函数。 而对其类型的划分通常可以分为planar、linear、scttar 等不同类型。 对此，本文将该算法设计为如下：

第一，构造协方差矩阵M，对该任意点p 的3*3 矩阵的特征值进行计算，并按照降序的方式进行排列，其大小分为表示为λ1，λ2，λ3， 而与上述相对应的单位特征向量则为e1，e2，e3，因此，根据上述的特征值的计算，则可以得到如下的相关参数：

其中上述计算的3 个参数当中，如其中的a1为最大，则将点p 表示为linear；如a2最大，则将p 定义到planar，以此类推。

第二，通过对其变换参数的初始化和对对应点的求解，可得到其目标函数。如果两个点其都为planar 类型的点，则其目标函数则为：

其中Vwi-1（q）表示为在没有进行配准前其存在的三维世界坐标。 对此，可将公式（6）变幻为：

最终通过奇异值分解对其求解。

4 结果验证

通过对上述算法的设计， 文中首先采用视觉对比的方式对图像的好坏进行评价，而开发工具则采用美国微软公司开发的Visual Studio 2012，计算机内存为4G，显卡内存为1G。 在实验当中国其全局数据立方体中的体素个数为k*k*k，k=512。

通过对图像3 的重建，则可得到图像4 的效果，其具体如图3、图4 所示。

图3 对象1Fig. 3 The object 1

同时通过对其实验误差的统计， 并将其与传统的方法进行统计，可以得到如表1 所示的误差分析结果。

5 结束语

图4 图像重建过程Fig. 4 Image reconstruction

表1 实验误差情况（mm）Tab. 1 Experimental error （mm）

文中针对在采用传感器进行深度图像获取中， 针对其图像精准度比较低的问题通过采用分类的方法进行配准算法设计，实现了在视觉效果的增加，减小了误差，说明该方法具有一定的实用性。

[1] 贾云得. 机器视觉[M]. 北京:科学出版社，2000.

[2] 宋诗超. 基于Kinect的三维人体建模与测量的研究[D]. 上海:东华大学，2013.

[3] 张翠红. 基于Kinect深度相机的室内三维场景重构[D]. 大连:大连理工大学，2013.

[4] 郭连朋，陈向宁，刘彬，等. 基于Kinect传感器多深度图像融合的物体三维重建[J]. 应用光学，2014（5）:811-816.GUO Lian-peng，CHEN Xiang-ning，LIU Bin，et al. Multi depth Kinect sensor image fusion in 3D reconstruction based on [J]. Applied Optics，2014（5）:811-816.

[5] 杨鸿，钱堃，戴先中，等. 基于Kinect传感器的移动机器人室内环境三维地图创建[J]. 东南大学学报：自然科学版，2013（S1）:183-187.

YANG Hong，QIAN Kun，DAI Xian-zhong，et al. A 3D map of indoor environment for mobile robot Kinect sensor based on creating[J]. Journal of Southeast University :Natural Science Edition，2013（S1）:183-187.

[6] 徐祯琦，龚光红. 基于Kinect的物体表面重建方法研究[J].中国体视学与图像分析，2013（3）:255-262.

XU Zhen-qi，GONG Guang-hong. Based on surface reconstruction method Kinect[J]. Chinese Stereology，2013（3）:255-262.