让“活动”触及数学本质

濮志坚

摘 要：现行的新课标由双基变四基，其中新增了“基本活动经验”这一项。“基本活动”是带给“经验”生长的力量，但如果盲目追从，那效果会适得其反。在活动前指引孩子探究的方向、在活动中注重孩子思维的层次、在活动后触及概念的本质，才能使他们的原初经验得以改造和提炼，完成数学活动经验从低层次到高层次的生长。

关键词：基本活动；探究方向；思维层次；概念本质；活动经验

新一轮基础教育课程改革后，随着“双基”走向“四基”，一线教师都有意识地围绕“四基”目标设计教学过程、组织教学活动，而且特别在“基本活动经验”这一目标上下工夫。那么，怎样的“数学活动”才是好的数学活动，更有利于让孩子在探索中发现问题、解决问题，从而积累“经验”呢？笔者有以下几点想法，与同行探讨。

一、活动前，引导探究方向

在“三角形的三边关系”这一教学中，为了解决“三角形的三条边有什么关系”，常会设计如下操作：小组合作用4厘米、6厘米、10厘米、12厘米四根小棒拼三角形，哪三根小棒能围成三角形，哪三根不能围成三角形，并记录在表格中。活动安排看似很合理，但学生在拼三角形时，关注点是在“能不能围成”上，而不是在“边的长短”上，最后到交流、比较三边关系，需要学生感悟概念的本质时，课堂会出现“卡壳”现象，学生很难用语言解释其中的所以然。因此，笔者认为在活动前应引导学生明确真正的操作目的，提出问题，再让学生带着问题去探究。其对应的活动如下：

师：同学们，上节课我们已经学过了“三角形是由三条线段围成的”，那么，是不是任意三条线段都能围成三角形呢？

生：不是。一条10厘米，另外两条都是1厘米，就不能围成。

师：大家想象一下围的情况。咱们一起在纸上画画看，能不能围成呢？

（学生画，体会为不成，教师在黑板上画出相似图形）

师：还能举例吗？

学生举例，并再次尝试用画三角形来验证。

师：看来，用三条线段围三角形，有的能围成，有的却不能围成，到底这三条线段的长短之间有什么关系呢？下面我们来动手研究一下。

如上教学，使探究活动更有价值。这个过程不再是一个通过灌输实现的被动过程，而是在个人积极主动参与探究活动的过程中实现的。同时，操作活动结束后，使学生更容易通过比较归纳出三边关系的本质。

二、活动中，关注思维层次

在教学“小数的性质”过程中，有教学片断如下：

师：我两个表妹的身高分别是1.5米和1.6米，我的身高正好夹在她们的身高之间，谁来猜一猜？

生猜测：1.53米…1.58米

师：猜对了，我的身高就是1.58米。能不能把我的身高画下来？

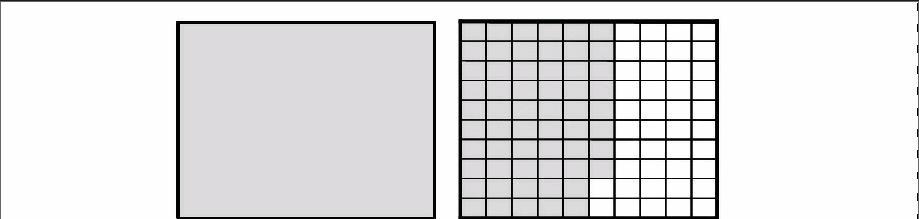
教师出示作业纸（第二个长方形的左边的宽划分成了10格的线段）：

学生开始动手画图，教师在下边巡视。

开始交流汇报了，教师展示学生作品（1）。

作品（1）：

师：这位同学是怎么想的？

生：我先画了1.6米，再画0.08米。

师：最后一条表示0.08米吗？

生：不能确定，大约是0.08米。

师：我们来看作品（2）。

作品（2）：

师：这一种，隔开了一条线段，他是怎么分的？

生：因为第一条平均分了10份，所以，只要画一条线段就能表示出0.08米。

师：这种相比第一种，更精确了些。

师：我们来看作品（3），他是怎么表示的？

作品（3）：

生：作品（3）是将第6条平均分成10格，画其中的8小格。

师：这种表示方法好在哪里？

生：我们一看就能知道了，一目了然。

师：我们最后听一听与众不同的那个孩子的故事。

作品（4）：

师：这位同学是怎样表示的？

生：我是把第二个长方形平均分成100份，取其中的58份，就表示出了1.58米。

我们不得不佩服这位教师的智慧。先是让学生通过数形结合的方法，展开开放式的操作活动；再是通过活动中的巡视，发现了学生的不同方法，了解到了学生不同的思维层级；最后通过展示不同的分割方法，逐渐领悟两位小数的含义。这样的教学使知识形成的过程一步步来得更加从容又富有深度，达成了知识性目标层次性的一个个飞跃。

三、活动后，触及概念本质

如三角形稳定性教学，老师让学生比赛拉三角形和平行四边形木架，拉动的获胜，来体验三角形的稳定性。然后教师让学生来回答拉三角形的学生失败的原因，学生肯定能异口同声地回答，是因为三角形具有稳定性，而且更“牢固”。热闹的活动，学生学得高兴，印象也很深刻。然而热闹之后再思考，却发现学生“深刻的印象”其实只停留在使劲“拉”，“拉”不动，就具有稳定性。其实，这一数学活动体验的是牢固性。三角形稳定性是指“三角形三条边长度确定，其大小、形状也就确定”。其对应的活动应该是：

师：你们能用同样的三根小棒围不同的三角形吗？（学生开始动手活动）

师：通过刚才的活动，请你比较同桌之间的三角形，发现了什么？

生：我发现我们围成的小棒形状和大小都完全一样。

师：是啊，当三角形的三条边长确定时，大小、形状也就确定了，这就是三角形的稳定性。

师：那么，请你用相同的四根小棒围平行四边形，你又会发现什么呢？（学生操作、比较）

生：我发现可以围成不同的形状，有长方形和不同的平行四边形。

师：是啊，这说明平行四边形具有不稳定性。

有经历，不一定有经验，没有经历，一定没有经验。学生经历了触及数学本质的、多样化的数学活动，完成数学活动经验从低层次到高层次的生长。

编辑 孙玲娟