基于内置重复控制器改进无差拍的 有源滤波器双滞环控制方法
2015-08-24张宸宇郑建勇周福举郭邵卿
张宸宇 梅 军 郑建勇 周福举 郭邵卿
基于内置重复控制器改进无差拍的 有源滤波器双滞环控制方法
张宸宇梅军郑建勇周福举郭邵卿
(东南大学电气工程学院 南京 210096)
采用内置重复控制器的方法弥补无差拍算法和离散控制系统中的周期性误差,通过对内置重复控制器的设计保证了系统的稳定裕度和稳态准确度。针对内置重复控制器动态性能差的缺点,采用基于空间矢量的滞环控制策略,结合双滞环控制思想,当误差电流落入内环时,使用最优矢量调制得到精确的开关状态;当误差电流落入外环时,使用最快矢量控制迅速减小误差电流到达新的稳态。仿真和实验皆验证了所提出的控制方法具有良好的稳态控制准确度和暂态响应速度。
有源电力滤波器 无差拍 重复控制 双滞环
0 引言
作为动态谐波治理装置,并联有源电力滤波器(Active Power Filter, APF)的电流控制策略对补偿效果起着决定性的作用[1-6]。无差拍控制是离散采样控制系统特有的一种控制方式,具有数学推导严密、稳态跟踪准确度高等优点[7],因此被广泛应用于有源滤波器的控制中。然而无差拍控制实际上是一种开环控制,其良好的电流跟踪效果需要有合适的电流预测方案来保证,没有预测的无差拍控制实际上是差一拍甚至是差两拍控制,所以有效地预测到下一拍或者下两拍桥臂输出电流对系统的准确度起到决定性作用。文献[8]采用平推法,利用检测指令值代替下一拍的预测值,这是一种差一拍控制。文献[9]提出一种无差拍控制策略,采用上一基波周期谐波电流采样值,作为下一周期谐波电流预测值,虽然稳态时没有误差,但动态时有一个电网周期延时。文献[10]采用自适应谱线增强器预测两拍后的电流状态,但是由于横向滤波器维数大,计算繁琐,不易实现离散化。
由于重复控制可消除周期性误差,诸多学者将其引入至无差拍控制中。文献[7]采用重复预测型观测器,通过闭环状态观测器有效地提高了预测准确度。文献[11]则利用重复控制器修正无差拍控制中的控制偏差,得到下一拍的输出电压矢量。但是重复控制器的一个致命缺点是动态响应速度慢[12],在负载有功变化或突变的场合下,内置重复控制器往往有系统状态延时。针对此,文献[13]采用平推法结合重复预测控制来改善动态特性;文献[14]则采用一种快速重复控制策略,它的重复周期只有传统重复控制的一半。虽然这些方法都能在一定程度上改善系统动态响应,却不能从根本上解决内置重复控制器造成的延时问题。
本文通过设计内置重复器的无差拍控制算法,并从稳定裕度和稳态准确度的角度考虑设计重复控制器参数,有效获得了两拍后的桥臂电流数值,弥补了离散采样系统的一拍固有延时和无差拍控制的一拍周期性延时。在此基础上,为解决内置重复控制器动态响应慢、无差拍控制算法运算量大的缺点,结合双滞环控制理论[15],采用基于空间矢量的滞环电流控制(Hysteresis Current Control based Space Vector Modulation, HCC-SVM)。电流内环采用最优矢量控制,根据误差电流矢量和内置重复控制器的无差拍算法计算电压参考矢量,确定当前时刻的开关状态;电流外环采用最快矢量控制,只要误差电流矢量进入外环,则不用计算电压参考矢量,直接选择能够消除当前最大误差电流相的开关状态,使得误差电流迅速回到内环。改进后的方法在保证稳态跟踪准确度的同时,有效地提高了系统暂态响应速度,仿真及实验均证明了本文所提方法的有效性和可行性。
1 无差拍控制系统
采用无差拍控制有源电力滤波器系统结构及规定正方向如图1所示。
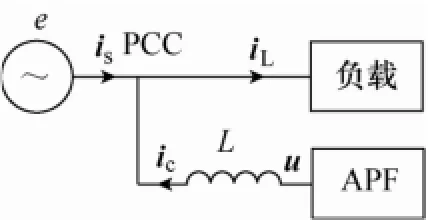
图1 系统结构Fig.1 System structure
根据图1所示正方向有
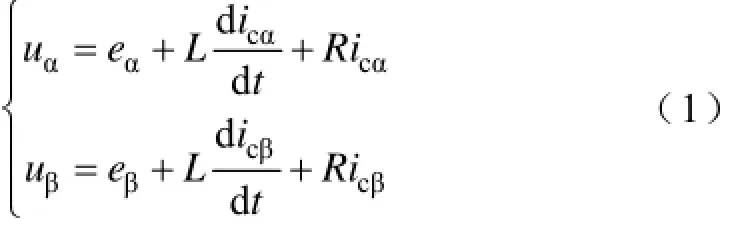
通过式(1)可得到精确的电压源逆变器(Voltage Source Inverter, VSI)输出电压u,通过电压矢量调制得到相对应的开关状态。对式(1)进行离散化

式(2)在第k个采样点计算得到VSI输出电压u(k),但在该采样周期内实际开关状态却是u(k-1),由上个周期的计算结果决定了这个周期的系统状态,如图2所示。

图2 差一拍控制时变流器侧电压指令作用时间示意图Fig.2 Function time sketch map of voltage instruction at the converter side with one-sampling-period delay
实际上,图2是由于采样控制系统和数字系统离散化存在固有的延时[16]。为了在k时刻得到下一个时刻采样,即k+1时刻VSI输出电压,式(2)

式中,I(k)=(icα(k), icβ(k))T;E=(eα(k), eβ(k))T, G= (1-RTs/L)E;H=(-L/Ts)E;U(k)=(uα(k)-eα(k), uβ(k)- eβ(k))T。
为消除采样、系统离散化带来的延时和无差拍控制差一拍的延时,同时可得到精确的k+1时刻逆变器输出电压U(k+1),系统需要在k时刻得到I(k+2)、I(k+1)和E(k+1)。首先通过式(3)在k时刻U(k)、I(k)和E(k)得到k+1时刻的I(k+1)

同样在系统电压不畸变情况下,很容易由E(k)直接得到E(k+1)

若采用平推预测法来获取,下一采样时刻的补偿电流I(k+2)=I*(k+1)。事实上,这是差一拍的预测方案,而且在负载电流变化较大时甚至得不到准确的I*(k+1)。

由式(7)可知,系统在k时刻,通过计算得到I(k+1)和E(k+1)的数值,只要能够预测到两拍以后的电流值I(k+2),就可在k时刻计算出下一时刻的逆变器输出电压U(k+1)。

由式(8)可知,能否在k时刻得到k+2时刻的桥臂电流成为无差拍控制稳态准确度的关键性因素。
2 内置重复控制器
2.1内置重复控制的无差拍控制策略
如果某周期出现的扰动在下一个周期的同一时刻重复出现,控制器根据参考信号与输出反馈信号之间的误差来确定校正信号,并在下一个周期将此校正信号叠加到原控制参考信号,即可有效抑制周期性扰动对输出信号的影响。比如对于系统本身设置的死区,或者有些驱动电路存在固有硬件延时,通过内置重复控制器可有效地解决[17-19]。
本文根据重复控制原理,采用内置重复控制器来修正由于平推预测两拍后桥臂电流造成的周期性的控制偏差,从而对VSI输出电压实现精确地无差拍控制,本文称之为最优矢量控制法。内置重复控制器的电流环控制结构如图3所示。
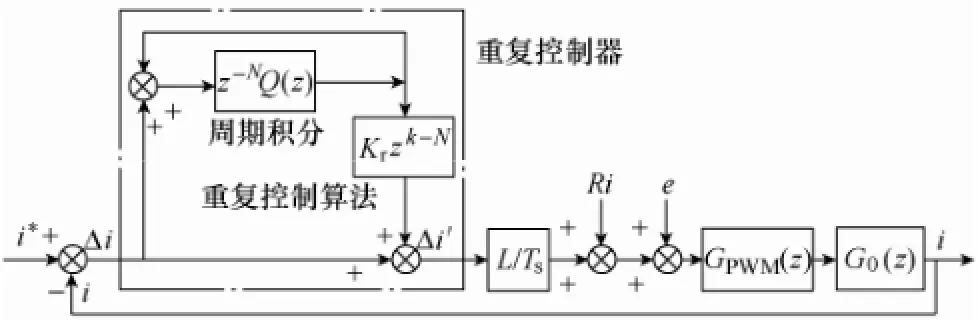
图3 内置重复控制器的电流环控制结构Fig.3 Structure of current loop control with plug-in repetitive controller
由图3可知,重复控制器包括周期积分环节和重复控制算法。z-NQ(z)为周期积分环节,N=fc/f0,fc为采样频率,f0为基波频率;Q(z)为衰减滤波器,为避免闭环系统因其失去稳定,实际内模中的Q(z)通常取低通滤波器或略小于1的常数[11]。Krzk-N是重复控制算法补偿器,目标是补偿器的幅值等于或略小于1,即将对象的中低频段增益校正为1;zk为超前补偿环节,k=Nθ/360,θ 为系统的延时相角。GPWM(z)是逆变器传递函数,一般可等效成一个跟随系统,将其简化为GPWM(z)=1。G0(z)为系统桥臂的传递函数,G0(z)=i(z)/(u(z) -e(z))。
2.2重复控制器设计
无差拍算法中内置重复控制器参数选择对系统稳定性非常敏感,且设计恰当可有效提高稳态控制准确度,所以其参数设计就变得尤为重要。为了对重复控制器的具体参数进行设计,图3可简化为图4。

图4 离散控制系统Fig.4 Discrete control systems
在图4中重复控制的传递函数为
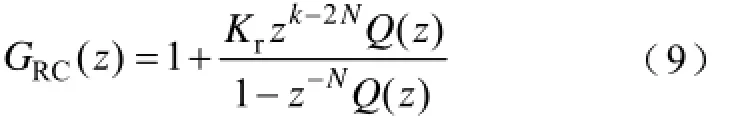
系统输出函数为
系统对于输入信号的闭环传递函数为
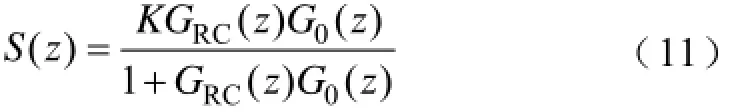
式中,分母即闭环传递函数的特征多项式P(z),即

将式(9)代入式(12)得到
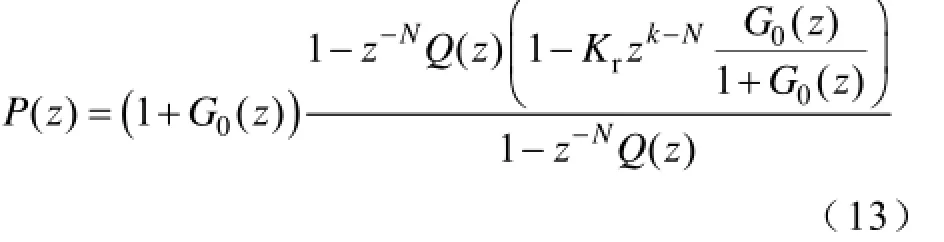
根据式(13),当输入和干扰信号都是周期信号且z-N=1,系统传递函数1+G0(z)有足够的稳定裕量时,根据小增益定理[20]可得到闭环系统稳定的充分条件是

由式(14)可知,|Q(z)|≤1是系统稳定的必要条件,且Q(z)越小闭环系统的稳定性越强。
为验证系统在稳态时的控制准确度,写出系统的误差传递函数Ge(z)
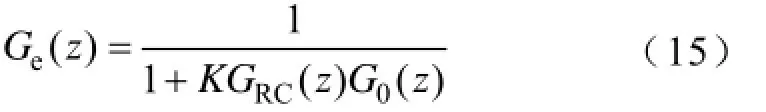
将式(9)代入式(15)可得
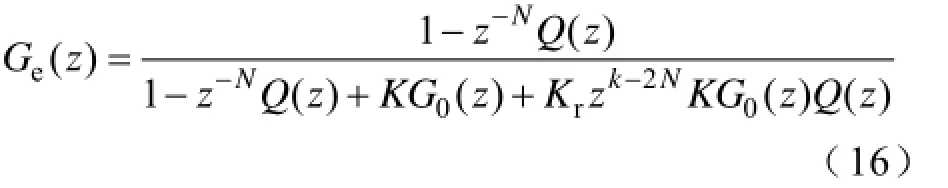
根据式(16),当Q(z)=1时,Ge(z)=0,此时内模相当于一个纯积分环节,意味着系统稳态传递误差为0;但是结合式(14),Q(z)的设计需要考虑系统的稳定性和稳态控制准确度。本文Q(z)取值为常数0.95,保证了系统具有一定稳定裕度的同时,可将误差衰减到原来的0.05倍[21]。
根据系统硬件实际选取,系统桥臂电感为0.5mH,内阻为0.1Ω,系统采样频率为10kHz,得到

将式(17)和Q(z)代入式(14),并且相位补偿因子k=2,则

通过式(18)可知为了提高系统稳定裕度,Kr取值趋近于0时稳定性越高,但是为了将中低频段增益校正为1,本文Kr折中取值0.5。
2.3电流闭环控制系统性能
内置重复控制内模开环伯德图如图5所示。
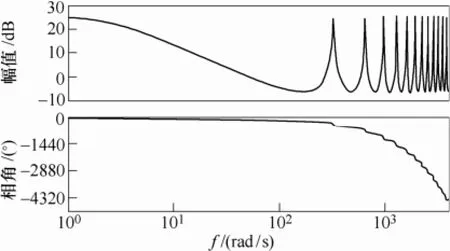
图5 重复控制器伯德图Fig.5 Bode diagram of repetitive controller
从重复控制器的伯德图可看出,系统在基波频率及其倍频处有较大幅值增益。由于重复控制器中的延时环节z-N使内模在基波频率处有360°相角滞后,即重复控制器可无静差跟踪周期性输入信号,但是对于动态过程要有一个延时才可起作用。
当预测电流控制器采用如图3所示的结构时,参数选择如本文推导,整个闭环电流控制系统伯德图如图6所示。

图6 闭环控制系统伯德图Fig.6 Bode diagram of closed loop control system
由图6可知,APF控制系统秉承了内核的特点,在设定频率处有较大幅值增益,但是整个系统由于超前环节传函无相位滞后。
3 HCC-SVM双滞环控制
内置重复控制器的无差拍控制可精确得到当前时刻的逆变器输出电压,通过基于空间矢量的滞环电流方法可获得当前时刻的开关状态。
由于内核中z-N的延时,使得重复控制动态响应速度缓慢[12],而无差拍控制需要大量的计算,对数字控制系统有一定的要求。为改善系统的动态特性和算法的运算速度,本文采用在复平面的双滞环误差电流控制方法[18]。
3.1HCC-SVM控制原理
对于系统状态方程式(1),当前状态下的桥臂输出电流矢量ic并不完全等于指令电流矢量ic*,存在一个误差电流矢量

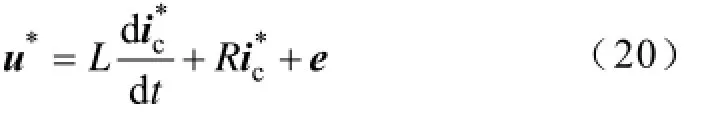
式中,u*为当前时刻的VSI精确参考输出电压,忽略输出滤波器内阻,式(20)和式(1)相减得到

根据式(2),在一个开关周期内认为指令电压u*是恒定的常数,因此HCC-SVM控制的问题就是如何去选择合适的开关状态u(k),使得合成电压矢量ueq=u*-u限制误差电流矢量δ 在一个很小的区域内,即使得ic能精确跟踪指令电流ic*。误差电流和参考矢量空间分布如图7所示。
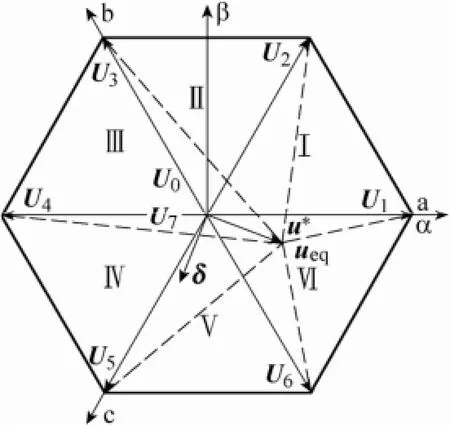
图7 误差电流和参考矢量空间分布Fig.7 Distribution of error current and reference vector
3.2双滞环控制策略
双滞环控制策略如图8所示,外环控制针对系统起动、负载突变或外界扰动的暂态情况。误差电流落在外环时采用最快矢量选择方法,不通过内置重复控制器的无差拍方法。无论参考电压矢量在哪个区域内,系统选择的开关状态能够最快减小误差电流||δ ||,使δ 回到内环。最快矢量控制实际上是一种单纯的αβ坐标系下滞环控制方法,系统具有优良的稳定性。当系统状态如图7所示时,则无论此刻参考电压矢量u*在哪个区域,开关状态的选择措施都是对误差最大的相电压,如图7所示,c相的误差最严重,则开关状态应选择U5。

图8 误差电流矢量区域判别Fig.8 Judgment diagram of current error vector
内环控制针对稳态运行状态。误差电流落在内环时采用最优电压矢量选择的方法[22],通过内置重复控制器的无差拍算法精确计算当前时刻VSI输出电压状态,在u所在区域内选择开关状态使得合成矢量ueq与误差电流δ 方向相反,如图7所示,δ 落入内环时则开关状态应选择U6,将桥臂输出误差电流控制在死区附近。
当δ 在死区内时,此刻误差电流控制已满足系统设定的稳态要求,VSI输出状态将不会改变,以降低平均开关频率,减小系统损耗。
4 仿真与实验
4.1仿真
为验证本文提出方法的可行性和正确性,基于Matlab2010b/Simulink建立如图1所示的系统模型。仿真系统参数为:380V工频三相交流电源,系统阻抗忽略不计;非线性负载为三相不控整流桥,RL=23Ω,APF直流侧采用6 800μF电解电容,直流侧稳定电压800V;输出滤波器为L滤波器,L=1mH。双滞环控制器,外环阈值为系统电流峰值的4%,内环阈值为系统电流峰值的2%。

图9 稳态仿真波形Fig.9 Static simulation diagrams
当系统处于稳态时,图9a从上到下分别是用平推法、内置重复控制器的无差拍得到的最优矢量控制法和基于双滞环的HCC-SVM控制方法下补偿后系统网侧电流波形。由图9a可知,当使用平推法时,在负载电流di/dt变化值点,由于离散系统状态依旧在上一拍,补偿滞后,网侧电流有畸变,THD为5.56%。而使用内置重复控制器的无差拍控制方法,由于系统一直处于稳态情况,系统一直工作在内环或者死区,即矢量状态的选择一直是最优矢量选择,所以稳态时是否采用双滞环对系统的影响不大,其网侧电流THD分别为0.78%和0.45%。
图9b、图9c分别是内置重复控制器的无差拍法得到的最优矢量控制和基于双滞环的HCC-SVM控制方法下稳态时αβ坐标中桥臂输出误差电流分布。由两图的对比可知,误差电流基本完全集中在内环和死区,稳态时两者差别不大。
为验证系统的动态性能,在仿真0.1s时刻投入二级负载,其阻抗与一级负载完全一样,RL=23Ω。在负载有功突变瞬间,图10a从上到下分别为负载侧电流波形、内置重复控制器的无差拍得到的最优矢量控制法和基于双滞环的HCC-SVM控制方法下补偿后系统网侧电流波形。从图10a可看出,系统状态突变时刻,采用最优矢量控制会出现电流跟踪松弛;而采用双滞环系统会立刻对误差电流最大的相做出反应,使误差电流立刻回到内环,跟踪效果改善显著,动态性能得到提升,网侧有功迅速响应负载有功变化。

图10 暂态仿真波形Fig.10 Dynamic simulation diagrams
图10b、图10c分别是内置重复控制器的无差拍得到的最优矢量控制法和基于双滞环的HCC- SVM控制方法下暂态时5个周期内αβ坐标中桥臂输出误差电流分布。由两图对比可知,图10b由于重复控制不能对负载变化立刻反应,最优矢量控制造成桥臂电流跟踪松弛,误差电流不能很好控制;而图10c误差电流基本控制在外环以内,偶尔有电流超出外环也会立刻回到外环内。
4.2实验
为进一步验证提出的控制策略正确性和可行性,在实验室搭建的50kV·A样机上进行验证实验。实验样机控制单元采用DSP芯片TMS320F28335结合FPGA芯片EP2C20F256,双核实现数据运算与逻辑功能。IGBT模块采用西门康SKM400GB176D,IGBT驱动采用西门康SKHI23/17(R)。样机的实验参数下表,实验其他参数同仿真。实验采用TEK示波器DPO2024和电能质量测试仪FLUKE43B对记录实验波形和数据。

表 实验样机参数Tab. Parameters of experiment prototype
分别采用平推法、内置重复控制器的无差拍得到的最优矢量控制法和基于双滞环的HCC-SVM控制法时,样机投网运行进入稳定状态后实验波形如图11所示。


图11 并网稳态实验波形Fig.11 Grid static experimental waveforms
由图11可知,采用内置重复控制器的无差拍控制算法可有效解决平推法所带来的一拍算法延时。当系统稳态运行时,是否采用双滞环控制对系统性能改变不大。采用三种算法下补偿前后网侧电流频谱如图12所示。

图12 系统补偿前后网侧电流THDFig.12 Current THD of system side before and after compensation
由图12可看出,网侧电流ηTHD从补偿前的25.6%通过平推法控制补偿到8.8%,但是由于系统状态依旧差一拍,通过内置无差拍控制器可消除这一拍周期性误差。网侧电流ηTHD稳态时降低到4.7%,而采用双滞环控制策略稳态时ηTHD为4.3%。
为进一步验证样机的动态性能,在样机运行过程投入二级负载,其阻值与第一级负载相同为23Ω。采用内置重复控制器的无差拍得到的最优矢量控制法和基于双滞环的HCC-SVM控制法的实验波形如图13所示。
通过图13a和图13b的对比可明显发现,图13a一直使用最优矢量控制策略,由于内置重复控制器不能立刻作出动态响应,电流跟踪松弛,动态响应时间t1约为18ms;图13b当负载电流突变时,误差电流落入外环,采用最快矢量控制,动态响应时间t2约为12ms,响应时间得到明显改善,使得电流误差迅速回到内环,系统达到新的稳态。
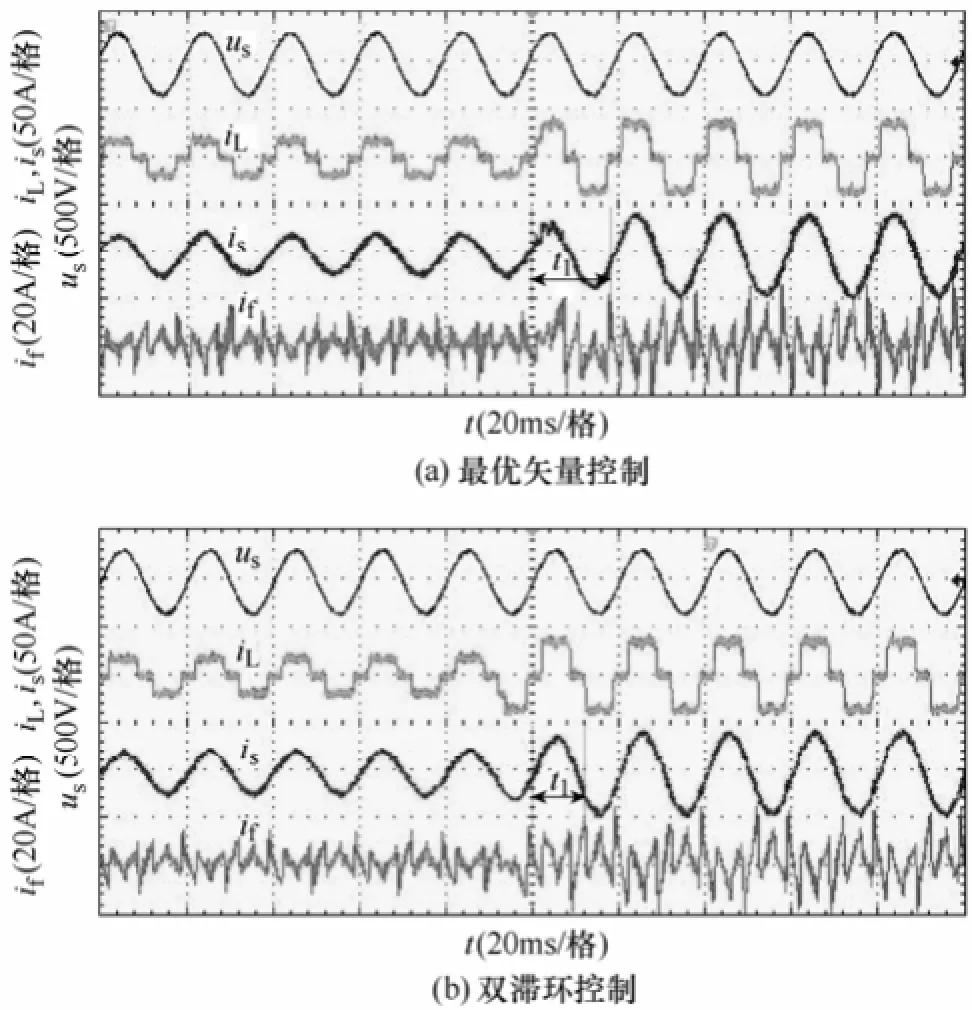
图13 并网暂态实验波形Fig.13 Grid dynamic experimental waveforms
5 结论
(1)针对没有预测的无差拍控制方法实际是差一拍或者差两拍控制,本文采用内置重复控制器修正由于无差拍算法和离散控制系统造成的周期性 误差。
(2)通过对重复控制器参数的设计,电流闭环控制系统既有充分的稳定裕度又有足够的稳态准确度。
(3)采用HCC-SVM调制方法,结合双滞环控制理论,内环保证了系统有足够的稳态控制准确度,外环保证了暂态情况下的系统动态响应速度。
改进后的方法在保证稳态跟踪准确度的基础上,有效地提高了系统暂态响应速度,适于现代化工业现场的谐波电流治理。仿真和实验均验证了本文所提控制方法的有效性和可行性。
[1] Ghennam T, Berkouk E M, Francois B. A novel space-vector current control base on circular hysteresis areas of a three-phase neutral-point-clamped inverter[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2669-2678.
[2] 罗安. 电网谐波治理和无功补偿技术及装备[M]. 北京: 中国电力出版社, 2006.
[3] Smedley K M, Zhou Luowei, Qiao Chongming. Unified constant-frequency integration control of active power filters-steady-state and dynamics[J]. IEEE Transactions on Power Electronics, 2001, 16(3): 428-436.
[4] 杨秋霞, 高金玲, 赵晔, 等. 有源电力滤波器的特定次谐波控制策略[J]. 电力系统保护与控制, 2012, 40(3): 119-123. Yang Qiuxia, Gao Jinling, Zhao Ye, et al. Research on specific harmonic control strategy for active power filter[J]. Power System Protection and Control, 2012, 40(3): 119-123.
[5] 沈玲菲, 危韧勇, 徐保友, 等. 一种新型的有源电力滤波器直接功率控制方法[J]. 电力系统保护与控制, 2013, 41(4): 91-96. Shen Lingfei, Wei Renyong, Xu Baoyou, et al. A novel APF direct power control approach[J]. Power System Protection and Control, 2013, 41(4): 91-96.
[6] 邱银锋, 梁志珊. 无需检测负载有功电流的一种APF 无源性控制方法[J]. 电力系统保护与控制, 2012, 40(23): 80-86. Qiu Yinfeng, Liang Zhishan. Passivity-based control of APF with no load active current detection[J]. Power System Protection and Control, 2012, 40(23): 80-86.
[7] 何英杰, 刘进军, 王兆安, 等. 基于重复预测原理的三电平APF无差拍控制方法[J]. 电工技术学报, 2010, 25(2): 114-120. He Yingjie, Liu Jinjun, Wang Zhaoan, et al. A deadbeat control algorithm based on repetitive predictor theory for three-level active power filter[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 114-120.
[8] 王文, 罗安, 徐先勇, 等. 有源滤波器双滞环空间矢量离散控制方法[J]. 中国电机工程学报, 2013, 33(12): 10-16. Wang Wen, Luo An, Xu Xianyong, et al. A dual-hysteresis space-vector discrete control method for active power filters[J]. Proceedings of the CSEE, 2013, 33(12): 10-16.
[9] 韩郁, 詹长江, 赵良炳, 等. 三电平并联型电能质量调节器的控制技术研究[J]. 清华大学学报, 2000, 40(3): 40-43. Han Yu, Zhan Changjiang, Zhao Liangbing, et al. Control of tri-level shunt power quality conditioners[J]. Journal of Tsinghua University, 2000, 40(3): 40-43.
[10] Nishida K, Rukonuzzman M, Nakaoka M. Advanced current control implementation with robust deadbeat algorithm for shunt single-phase voltage-source type active power filter[J]. IEE Proceedings on Electric Power Applications, 2004, 151(3): 283-288.
[11] 周娟, 秦静, 王子绩, 等. 内置重复控制器无差拍控制在有源滤波器中的应用[J]. 电工技术学报, 2013, 28(2): 233-238. Zhou Juan, Qin Jing, Wang Ziji, et al. Application of deadbeat control with plug-in repetitive controller in active power filter[J]. Transactions of China Electro- technical Society, 2013, 28(2): 233-238.
[12] 武健, 何娜, 徐殿国. 重复控制在并联有源滤波器中的应用[J]. 中国电机工程学报, 2008, 28(18): 66-72. Wu Jian, He Na, Xu Dianguo. Application of repetitive control technique in shunt active power filter[J]. Proceedings of the CSEE, 2008, 28(18): 66-72.
[13] 张国荣, 邵竹星, 陈林. 基于改进重复预测原理的并联有源电力滤波器无差拍控制策略[J]. 农业工程学报, 2012, 28(13): 172-178. Zhang Guorong, Shao Zhuxing, Chen Lin. Deadbeat control strategy of shunt active power filter based on repetitive predictor theory[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(13): 172-178.
[14] 宫金武, 查晓明, 陈佰锋. 一种快速重复控制策略在APF中的实现和分析[J]. 电工技术学报, 2011, 26(10): 110-117. Gong Jinwu, Zha Xiaoming, Chen Baifeng. Analysis and realization of a fast repetitive controller in active power filter system[J]. Transactions of China Electro- technical Society, 2011, 26(10): 110-117.
[15] 姜俊峰, 刘会金, 陈允平, 等. 有源滤波器的电压空间矢量双滞环电流控制新方法[J]. 中国电机工程学报, 2004, 24(10): 82-86. Jiang Junfeng, Liu Huijing, Chen Yunping, et al. A novel double hysteresis current control method for active power filter with voltage space vector[J]. Proceedings of the CSEE, 2004, 24(10): 82-86.
[16] 漆铭钧, 罗安, 刘定国, 等. 有源电力滤波器参考电流的预测方法及其实现[J]. 中国电机工程学报, 2009, 29(7): 128-134. Qi Mingjun, Luo An, Liu Dingguo, et al. Prediction of the reference current of active power filter and its realization[J]. Proceedings of the CSEE, 2009, 29(7): 128-134.
[17] Aurelion G, Omar P, Vicente F, et al. Application of a repetitive controller for a three-phase active power filter[J]. IEEE Transactions on Power Electronics, 2007, 22(1): 237-245.
[18] Ramon C, Robert G, Enric F. Odd-harmonic digital repetitive control of a single-phase current active filter[J]. IEEE Transactions on Power Electronics, 2004, 19(4): 1060-1068.
[19] 于晶荣, 粟梅, 孙尧. 有源电力滤波器的改进重复控制及其优化设计[J]. 电工技术学报, 2012, 27(2): 235-241. Yu Jingrong, Su Mei, Sun Yao. Improved repetitive control and its optimization for active power filter[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 235-241.
[20] Zhou Keliang, Wang Danwei. Unified robust zero-error tracking control of CVCF PWM conver- ters[J]. IEEE Transactions on Circuits System I: Fundamental Theory and Applications, 2002, 49(4): 492-501.
[21] 梅红明, 刘建政. 基于电流观测器的三相变流器重复控制方法[J]. 中国电机工程学报, 2011, 31(27): 59-65. Mei Hongming, Liu Jianzheng. A repetitive control method of three-phase VSC based on current state observer[J]. Proceedings of the CSEE, 2011, 31(27): 59-65.
[22] 曾江, 刁勤华, 倪以信, 等. 基于最优电压矢量的有源电力滤波器电流控制新方法[J]. 电力系统自动化, 2000, 24(6): 25-31. Zeng Jiang, Diao Qinhua, Ni Yixin, et al. A novel current control method for active power filter based on optimal voltage vector[J]. Automation of Electric Power Systems, 2000, 24(6): 25-31.
张宸宇 男,1989年生,博士研究生,研究方向为谐波抑制与无功补偿。
梅 军 男,1971年生,副教授,硕士生导师,研究方向为电力电子与电力传动。
Active Power Filter Double Hysteresis Method with Improved Deadbeat Control Based on Built-in Repetitive Controller
Zhang Chenyu Mei Jun Zheng Jianyong Zhou Fuju Guo Shaoqing
(Southeast University Nanjing 210096 China)
In this paper, a novel method built-in a repetitive controller is put forward to make up periodic error of deadbeat algorithm and discrete control system. The design of the plug-in repetitive controller ensures stability margin and steady precision of the system. Accounting for the poor dynamic performance of repetitive controller, the paper uses hysteresis control strategy based on space vector combined with double hysteresis control thoughts. When the error current falls into the inner ring, the accurate switching state can be obtained by the optimal vector modulation. While when the error current falls into the outer ring, the error current decreases to a new steady state through the fastest vector control. Simulation and experiment results both demonstrate the proposed method has good compensation effect of steady-state control accuracy and improved transient response speed.
Active power filter, deadbeat, repetitive control, double hysteresis
TN713
江苏省科技支撑计划资助项目(BE2012036、BE2013883)。
2013-10-15 改稿日期 2013-12-16
