Banach空间中分数阶微分方程解的存在性

胡雨欣, 寇春海, 葛富东

(东华大学 a. 理学院; b. 信息科学与技术学院, 上海 201620)

Banach空间中分数阶微分方程解的存在性

胡雨欣a, 寇春海a, 葛富东b

(东华大学 a. 理学院; b. 信息科学与技术学院, 上海 201620)

运用非紧性测度和Darbo不动点定理,研究了Banach空间中的分数阶微分方程初值问题解的存在性.

分数阶微分方程; 存在性; 非紧性测度; Darbo不动点定理

近30年来，分数阶微分方程已经从纯数学范畴逐步渗透到众多学科和工程应用领域，在材料力学、生物学、物理学、控制、多孔介质、电化学、黏弹性理论等方面都有广泛的应用.人们对分数阶微分方程基本理论的研究不再仅限于欧几里德空间,对于Banach空间中分数阶微分方程基本理论的研究也越来越多,主要围绕解的存在唯一性展开.关于Banach空间中非线性分数阶微分方程解的局部存在性问题,已有初步的研究成果,其研究方法一般是将分数阶微分方程转化成等价的Volterra积分方程,在适当的Banach空间中,运用不动点定理证明其存在性[1-8].而Banach空间中分数阶微分方程解的全局存在性问题尚未得到实质性的解决[9].

文献[8]研究了如下形式的分数阶微分方程初值问题解的局部存在性问题:

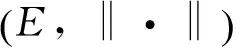
文献[9]研究了如下分数阶微分方程边值问题解的全局存在性问题：

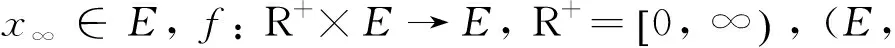
本文主要讨论如下分数阶微分方程初值问题：

(1)

其中:1<β<2, x0, x1∈E, f:R+×E→E是一个连续映射,(E, ‖·‖)是某个实Banach空间.这里运用非紧性测度和Darbo不动点定理,建立系统(1)在无穷区间上解存在的充分条件.

1　预备知识

定义1.1[10]函数x:R+→R的β阶(β>0)Riemann-Liouville分数阶积分定义为

其中:x使得上式在R+是逐点有定义的,Γ为Gamma函数.

定义1.2[10]函数x:R+→R的β阶(β>0)Caputo分数阶微分定义为

其中:n=[β]+1,t>β>0,x使得上式在R+是逐点有定义的.

注1.1对于值域属于Banach空间的抽象函数x,前面定义中的积分要在Bochner意义下考虑.

引理1.1[10]对β>0,有

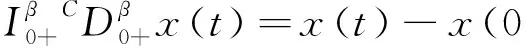
由引理1.1，经过简单的推算可以得到初值问题(1)等价的积分方程为

(2)

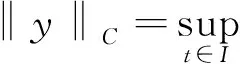
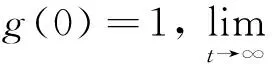
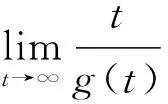
(3)

定义1.3称f: R+×E→E满足Caratheodory条件,如果

(1) ∀u∈E,t→f(t,u)在R+上强可测；

(2) 对于几乎所有的t∈R+,u→f(t,u)在E上连续.

下面给出非紧性测度的定义及其部分性质，更多内容请参阅文献[12-13].

设θ为Banach空间E的零元.记以x为中心,半径为r的闭球为B(x,r),特别的,记B(θ,r)为Br.

定义1.4非空有界子集D⊂E的Kuratowski非紧性测度α(D)定义为

α(D)=inf{d>0:

集合D能被有限个直径小于d的集合所覆盖}

根据定义易知，对于任意有界子集D,Y⊂E,Kuratowski非紧性测度α满足下列性质：

(1) 正则性.α(D)=0当且仅当D是相对紧集，特别的，单元素集的非紧性测度为0.

(2) 单调性.D⊂Y⟹α(D)≤α(Y).

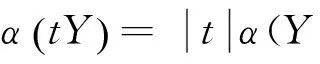
这里分别记α,αC,αX表示空间E,C(I,E),X中有界集的Kuratowski非紧性测度，可以得出以下几个引理.

引理1.2[13-14]若H⊂C(I,E)是有界且等度连续的，那么α(H(t))在I上连续且满足

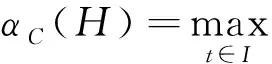
∫Iα(H(t))dt

引理1.3[13](Darbo不动点定理)假设X是一个Banach空间,D⊂X是一个非空有界闭凸子集,如果算子T:D→D是严格收缩的,那么算子T在D中至少存在一个不动点.

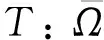
2　主要结果证明

为了采用Darbo不动点定理研究式(1)解的存在性,先将式(1)转换为等价的算子积分方程.由式(2)易知,式(1)的解在E中的存在性问题可以转换为下列算子T： E→E的不动点问题

假设映射f满足下列条件:

(A1) 映射f满足Caratheodory条件;

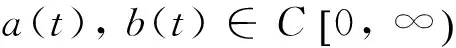
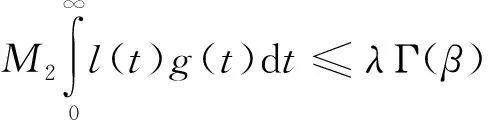
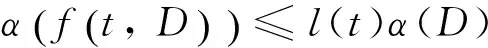
成立，其中0<λ<1.

定理2.1如果分数阶初值问题式(1)满足上述假定条件,那么,在E中至少存在一个解.

为了证明定理2.1,先给出以下几个引理.

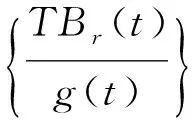
证明根据定义,由条件(A1)可得算子T是连续的.此外,对任意x∈Br⊂X,即存在常数r>0，满足‖x‖X≤r.这里有Tx(t)∈E,由条件(A2)可知

‖x0‖+‖x1‖M1+

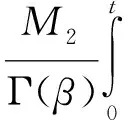
‖x0‖+‖x1‖M1+

‖x0‖+‖x1‖M1+r+

因此,T在Br上是有界的.

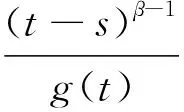
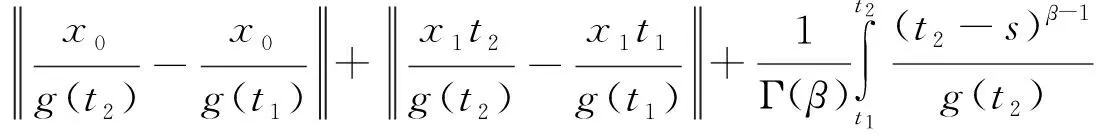
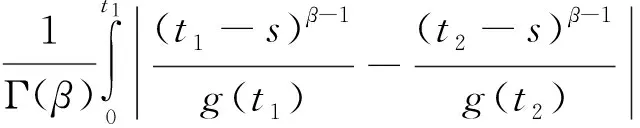
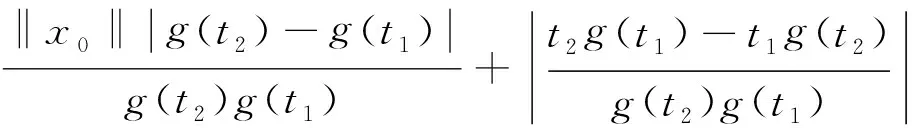
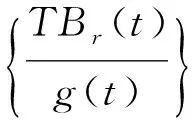
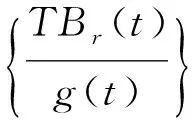
对任意的ε>0,当x∈Br时,由条件(A2)可知,存在常数L1>0,使得

(4)

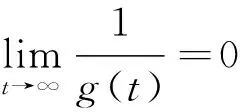
(5)

(6)

(7)

因此,对于任意的t1,t2≥N,根据式(4)～(7)得

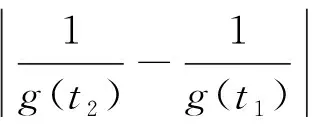
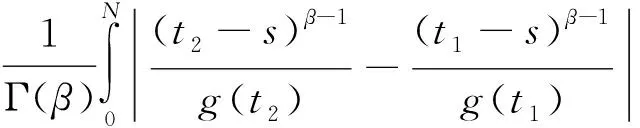
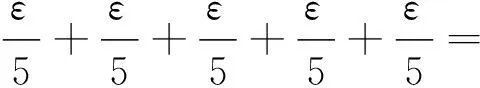
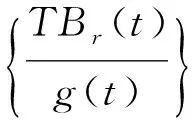
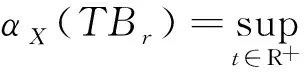
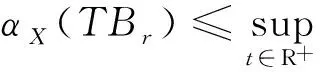
根据引理1.2,∀ε>0, ∃N>0,当t1,t2≥N时,对任意的x∈Br,都有

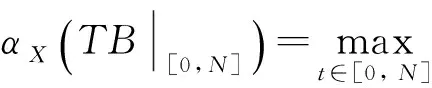
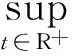
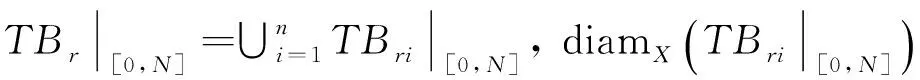
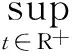
其中:diamX是X的有界子集的直径.

∀Tx1,Tx2∈TBri,t≥N,有

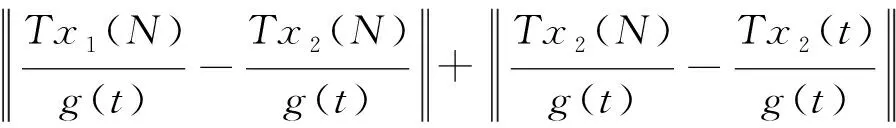
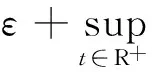
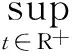
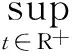
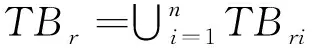
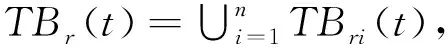
下面给出定理2.1的证明.

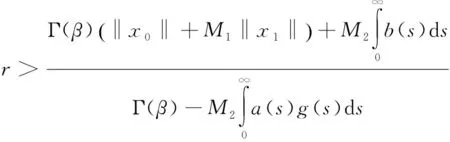
‖x0‖+‖x1‖M1+

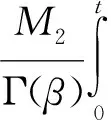
‖x0‖+‖x1‖M1+

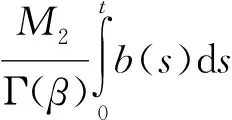
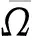
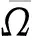
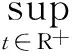
(8)

事实上,当t≤N时,由引理2.1可知，算子T是等度连续的,所以由引理1.2,有

根据引理2.1, ∀ε>0, ∃N>0,当t1,t2≥N时,对任意的x∈D,都有

因此，当t>N时，

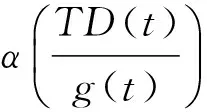
[1] BALACHANDRA K, KIRUTHIKA S, TRUJILLO J J. Existence results for fractional impulsive integrodifferential equations in Banach spaces[J]. Commun Nonlinear Sci Numer Simul, 2011, 16(4):1970-1977.

[2] NGUEREKATA G M. A Cauchy problem for some fractional abstract differential equation with nonlocal conditions[J]. Nonlinear Anal TMA, 2009, 70(5):1873-1876.

[3] SALEM H A H. Multi-term fractional differential equation in reflexive Banach space[J]. Math Comput Modelling, 2009, 49(3/4): 829-834.

[4] ARARA A, BENCHOHRA M, HAMIDI N, et al. Fractional order differential equations on an unbounded domain[J]. Nonlinear Anal TMA, 2010, 72(2): 580-586.

[5] BENCHOHRA M, GRAEF J R, MOSTAFAI F Z. Weak solutions for nonlinear fractional differential equations on reflexive Banach spaces[J]. Electron J Qual Theory Differ Equ, 2010(54): 1-10.

[6] LI K X, PENG J G, GAO J H. Nonlocal fractional semilinear differential equations in separable Banach spaces [J]. Electron J Differ Equ, 2013 (7): 1-7.

[7] LIANG J T, LIU Z H, WANG X H. Solvability for a couple system of nonlinear fractional differential equations in a Banach space[J]. Fract Calc Appl Anal, 2013, 16(1): 51-63.

[8] AGHAJANI A, POURHADI E, TRUJILLO J J. Application of measure of noncompactness to a Cauchy problems for fractional for differential equations in Banach spaces[J].Fract Calc Appl Anal, 2013, 16(4): 962-977.

[9] SU X W. Solutions to boundary value problem of fractional order on unbounded domains in a Banach space[J]. Nonlinear Anal, 2011, 74(8): 2844-2852.

[10] PODLUBNY I. Fractional differential equations [M]. London: Academic Press, 1999.

[11] KOU C H, ZHOU H C, YAN Y. Existence of solutions of initial value problems for nonlinear fractional differential equations on the half-axis[J]. Nonlinear Anal, 2011, 74(17): 5975-5986.

[12] BANAS J, GOEBEL K. Measures of noncompactness in Banach space[R]. Lect Notes Pure Appl Math, 60.New York: Marcel Dekker, 1980.

[13] GUO D J, LAKSHMIKANTHAM V, LIU X Z. Nonlinear integral equations in abstract spaces[M]. Dordrecht: Kluwer Academic Publishers, 1996.

[14] LAKSHMIKANTHAM V, LEELA S. Nonlinear differential equations in abstract space[M]. Oxford: Pergamon Press, 1981.

Existence of Solutions for Fractional Differential Equations in a Banach Space

HUYu-xina,KOUChun-haia,GEFu-dongb

(a. College of Science; b. College of Information Science and Technology, Donghua University, Shanghai 201620, China)

By utilizing the techniques of measures of noncompactness and the Darbo’s fixed point theorem, the existence of solutions of initial value problem for fractional differential equations in a Banach space is investigated.

fractional differential equations; existence; measure of noncompactness; Darbo’s fixed point theorem

1671-0444(2015)06-0867-06

2014-06-05

中央高校基本科研业务费专项基金资助项目(CUSF-DH-D-2014061)

胡雨欣(1989-),女, 山西平遥人, 硕士研究生, 研究方向为分数阶微分方程. E-mail：huyuxin2012@126.com

寇春海(联系人),男,教授,E-mail：kouchunhai@dhu.edu.cn

O 175.6

A