基于不确定性优化模型的空气质量管理

刘　敏，郑川江，陆海清国网浙江省电力公司电力科学研究院，浙江杭州310014

基于不确定性优化模型的空气质量管理

刘敏，郑川江，陆海清
国网浙江省电力公司电力科学研究院，浙江杭州310014

针对空气质量管理系统存在的多重不确定性与复杂性，基于区间线性规划（ILP）、随机数学规划（SMP）和模糊可能性规划（FPP）方法，研究开发了区间随机模糊可能性规划（ISFPP）模型以实现有效管理政策的制订。开发的ISFPP模型不仅能够处理多重不确定性，而且能够反映系统复杂性。同时，ISFPP模型能够分析不同置信水平下的管理情景。将ISFPP模型应用到一个假设的空气质量管理案例中，结果表明，置信水平的变化，可能导致系统总成本、污染物处理量及超标排放量发生相应的变化；在不同的置信水平下，生产企业能够选择合适的污染物控制措施，确定合理的污染物处理量和超标排放量。因而，模型结果能够用于生成决策方案，进而帮助决策者制订有效的管理政策。

空气质量管理；优化模型；区间线性规划；随机数学规划；模糊可能性规划；不确定性

刘敏，郑川江，陆海清.基于不确定性优化模型的空气质量管理［J］.环境工程技术学报，2015，5（2）：97-105.

LIU M，ZHENG C J，LU H Q.Air quality management based on an inexact optimization model［J］.Journal of Environmental Engineering Technology，

2015，5（2）：97-105.

由于高耗能行业对化石能源需求的不断增长，化石能源（尤其是煤炭）消耗日益增大，导致二氧化硫（SO2）和氮氧化物（NOx）等大气污染物排放增加。SO2和NOx能够造成空气污浊，对人体呼吸器官和皮肤产生刺激性；同时，也是酸雨、光化学烟雾形成的主要物种或引发物，对人类生产和生活产生严重影响［1］。因此，在空气质量管理系统中，运用优化方法，构建优化模型，制订行之有效的管理政策。然而，空气质量管理系统是个复杂的系统，包括污染物产生、污染物处理措施选择、污染物超标排放等；同时，由于可利用信息的匮乏以及偏颇的判断，系统元素具有不确定性，从而导致有效管理政策实现的困难。

针对空气质量管理系统存在的不确定性与复杂性，学者提出了一系列的不确定性优化方法［2-9］，例如，区间线性规划方法、两阶段随机规划方法、模糊鲁棒规划方法、机会约束规划方法、联合概率规划方法和多目标规划方法等。区间线性规划（ILP）方法能够有效地处理系统中存在的、表示为离散区间数的不确定性信息。ILP方法允许不确定性信息直接与优化过程及输出结果相联系，而且，它不会导致复杂的中间子模型，不需要模型参数的分布信息［10］。随机数学规划（SMP）方法能够有效地处理系统中存在的随机不确定性信息，随机变量的分布形式表现为概率密度函数。模糊可能性规划（FPP）方法能够利用模糊集合理论处理系统中存在的模糊不确定性信息。在建模过程中，具有可能性分布的模糊参数将引入模型框架中。ILP、SMP和FPP方法已经运用于空气质量管理领域［11-17］。每种方法能够有效地处理表示为单一形式的不确定性信息，但是，在处理多重不确定性问题方面存在不足。因此，在空气质量管理系统中，为了更好地处理多重不确定性信息，以及反映系统的复杂性，ILP、SMP和FPP方法被整合进一个基本的模型框架中，从而导致区间随机模糊可能性规划（ISFPP）方法的产生。在系统存在不确定性与复杂性条件下，很少有研究关注ISFPP方法在空气质量管理方面的应用。

笔者基于ISFPP方法，开发ISFPP模型，应用于空气质量管理。开发的ISFPP模型不仅能够处理表示为离散区间数、概率密度函数和模糊隶属函数的多重不确定性，而且能够反映系统的复杂性。同时，ISFPP模型能够分析不同置信水平下的管理情景。

1　优化模型的构建及求解

在空气质量管理系统中，电力能源以及钢铁、水泥等资源的生产，需要消耗大量的化石能源，进而产生大量的SO2与NOx污染物。因此，在空气质量管理系统中，为了控制SO2与NOx的排放量，基于SO2与NOx的排放标准和环境空气质量标准，选择合适的污染物控制措施，确定每种措施处理污染物的量。进一步，在空气质量管理系统多重不确定性条件下，确定合适的污染物控制措施及处理量，实现系统总成本的最小化。

1.1大气污染物扩散模型

在一定的气象条件下，对于任意的下风向位置，高架连续点源污染物扩散的地面浓度能够通过高斯扩散模型进行评估，模型能够被表示为［18］：式中：C(x，y)为高架点源的污染物地面浓度，mg/m3；Q为源强（单位时间内污染物排放量），mg/s；x为污染源排放点至下风向上任意点的距离，m；y为烟气中心轴在直角水平方向上到任意点的距离，m；H为烟囱的有效高度，m；u为平均风速，m/s；δy为侧向扩散系数，污染物在y方向分布的标准偏差，m；δz为竖向扩散系数，污染物在z方向分布的标准偏差，m。δy、δz与大气稳定度和水平距离x有关，其数值能够通过Pasquill-Gifford（P-G）扩散曲线进行估算［18］，或通过GB/T 3840—91《制定地方大气污染物排放标准的技术方法》提供的方法进行计算［19］。对于污染物地面浓度，描述单位污染物排放率的转化系数可以表示为：

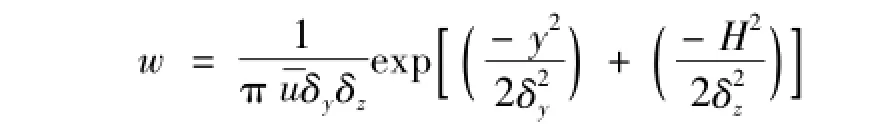
从而，

1.2ISFPP模型的构建

在空气质量管理系统中，许多系统参数具有不确定性以及参数之间的相互关系具有复杂性。污染物控制措施处理效率、电能负荷和资源产量等参数不能完全表示为确定值，并且它们的分布信息无法获取，这类不确定性信息被表示为离散区间数。污染物产生量是个随机事件，污染物产生率的不确定性信息被表示为概率密度函数。经济数据和污染物排放速率限值等参数是模糊的，但是，它们的可能性分布信息可以获取，这类不确定性信息被表示为模糊隶属函数。因此，为了反映系统多重不确定性及复杂性，实现有效的空气质量管理，基于ILP、SMP和FPP 3种不确定性优化方法，ISFPP模型能够被表示为：

目标函数

式中：i为排放污染物的生产企业；j为SO2的控制措施；r为NOx的控制措施；h为SO2产生的概率水平；t为NOx产生的概率水平；d为敏感点；~f±为规划期内的系统总成本，元；C~Sij为企业i利用控制措施j处理SO2的单位成本，元/mg；C~Nir为企业i利用控制措施r处理NOx的单位成本，元/mg；D~Si为企业i超标排放SO2的单位成本，元/mg；D~Ni为企业i超标排放NOx的单位成本，元/mg；XSi±jh为在SO2产生水平h条件下，企业i在单位时间内利用控制措施j处理SO2的量，mg/h；XNi±rt为在NOx产生水平t条件下，企业i在单位时间内利用控制措施r处理NOx的量，mg/h；YSi±h为在SO2产生水平h条件下，企业i在单位时间内超标排放SO2的量，mg/h；YNi±t为在NOx产生水平t条件下，企业i在单位时间内超标排放NOx的量，mg/h；Ti±为企业i在单位时间内的电能负荷或资源产量，kW·h/h或kg/h；PSih为在SO2产生水平h条件下，企业i的SO2产生情景发生的概率；PNit为在NOx产生水平t条件下，企业i的NOx产生情景发生的概率；μi±h为在SO2产生水平h条件下，企业i的SO2产生率，mg/（kW·h）或mg/kg；νi±t为在NOx产生水平t条件下，企业i的NOx产生率，mg/（kW·h）或mg/kg；ηi±j为企业i利用控制措施j处理SO2的效率；θ±ir为企业i利用控制措施r处理NOx的效率；w±id为企业i在敏感点d的单位污染物排放率的转化系数，h/m3；E~Si为企业i的SO2排放速率限值，mg/h；E~Ni为企业i的NOx排放速率限值，mg/h；F~Sd为敏感点d的SO2地面浓度限值，mg/m3；F~Nd为敏感点d的NOx地面浓度限值，mg/m3；LG为规划期的时间跨度，h。

1.3ISFPP模型的求解

区间参数b±可以表示为b±=［b-，b+］=｛t∈b|b-≤t≤b+｝［20］。模糊参数的可能性分布能够以模糊集来表征。模糊参数~b=（（b-）-，（b-）+，（b+）-，（b+）+），当（b-）+=（b+）-时，~b表示为三角模糊集；当（b-）+＜（b+）-时，~b表示为梯形模糊集［21］。基于模糊集的截集理论，在每个置信水平α下，~b能够包含在闭区间［（1-α）（b-）-+α（b-）+及（1-α）（b+）++α（b+）-］内［22］，置信水平的量化以置信度表征，置信度的范围为［0，1］。因而，基于模糊集的截集理论与运算法则［22］，式（3）可以去模糊化，转化为不同置信水平下的区间随机规划模型；进而基于鲁棒两步法（RTSM）［23］，在每个置信水平下，区间随机规划模型可以转化为2个确定的子模型，这2个子模型分别关联目标函数区间值的上界和下界；最后，利用单纯型法，分别求解子模型。因此，在每个置信水平下，式（3）的解为：

ISFPP模型是基于3种优化方法（ILP、SMP和FPP）而形成的。在强化模型的实用性和有效性方面，每种优化方法都有独特的贡献。例如，利用ILP方法来处理区间不确定性问题，利用SMP方法来处理概率分布问题，利用FPP方法来处理模糊可能性分布问题。因而，在空气质量管理系统中，ISFPP模型不仅能够处理系统中存在的多重不确定性，而且能够反映系统的复杂性。同时，在不同的置信水平下，ISFPP模型能够实现空气质量管理的多种决策选择。

2　案例研究

2.1系统概况

在某个假定的、具有不确定性的空气质量管理系统中，3个生产企业（火电厂（C1）、钢铁厂（C2）和水泥厂（C3））被看作是污染物排放的污染源，它们排放的SO2和NOx影响着3个敏感区（D1、D2和D3）的空气质量（图1）。为了控制SO2和NOx的排放，以及满足敏感区的环境空气质量标准，每个生产企业分别利用3种SO2控制措施和3种NOx控制措施处理SO2和NOx。研究问题为：在系统存在多重不确定性与复杂性条件下，选择合适的SO2和NOx控制措施，确定合理的SO2和NOx处理量，以实现系统总成本的最小化。

图1　研究系统Fig.1The study system

表1　生产企业的污染物控制措施处理效率与单位处理成本及污染物超标排放单位成本Table 1Treatment efficiencies and unit treatment costs of pollutants control measures and unit costs of pollutants excess emission for production enterprises

表1列出了不同生产企业的污染物控制措施处理效率与单位处理成本及污染物超标排放单位成本。当污染物的排放速率超过其限值时，生产企业需要支付一定的污染物超标排放费用。表2列出了不同污染物的产生情景发生概率与产生率及生产企业的电能负荷或资源产量。基于研究时期的大气稳定度与平均风速以及水平距离与烟囱有效高度等参数，可以推算得到不同生产企业在敏感区的单位污染物排放率的转化系数（表3）。对于火电厂（C1）、钢铁厂（C2）和水泥厂（C3）3个生产企业，SO2的排放速率限值分别为（515，530，540，560）×106、（230，235，245，255）×106和（65，68，71，75）×106mg/h；NOx的排放速率限值分别为（190，200，205，215）×106、（88，93，98，103）×106和（40，42，44，47）×106mg/h。对于D1、D2和D33个敏感区，SO2的地面浓度限值分别为（0.079，0.082，0.085，0.089）、（0.093，0.097，0.099，0.103）和（0.042， 0.044，0.047，0.052）mg/m3；NOx的地面浓度限值分别为（0.054，0.057，0.059，0.064）、（0.077，0.081，0.083，0.087）和（0.038，0.042，0.044，0.048）mg/m3。由于系统多重不确定性的存在，数据信息被表示为离散区间数、概率密度函数或模糊隶属函数。此外，假定研究时期的时间跨度为90 d。

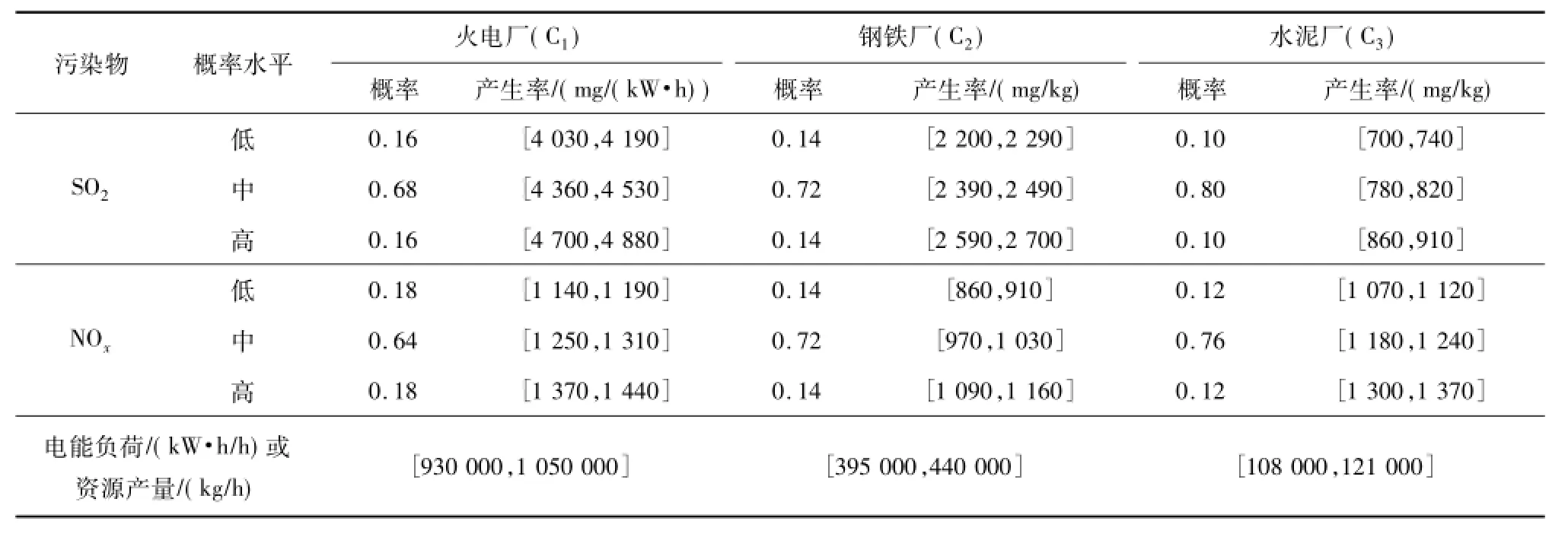
表2　不同污染物的产生情景发生概率与产生率及生产企业的电能负荷或资源产量Table 2Probabilities of scenarios occurrence and generation rates for different pollutants and electric power loads or resources amounts for production enterprises

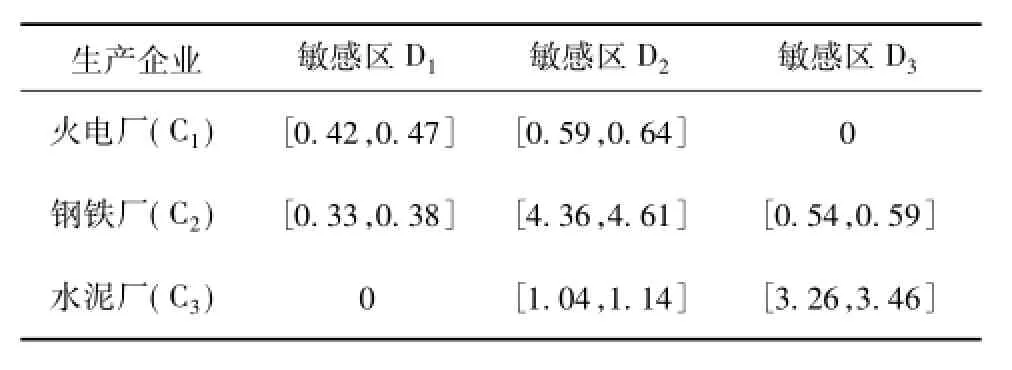
表3　不同生产企业在敏感区的单位污染物排放率的转化系数Table 3Conversion coefficients of unit pollutant emission rate at different production enterprises to sensitive areas 10-10h/m3

2.2结果分析

图2反映了不同置信水平下系统总成本的情况。在不同的置信水平下，所有的系统总成本都被表示为区间值；如果变量的实际值在其区间的上下界范围内变动，那么，系统总成本也将相应的在其区间的上下界范围内变化。由图2可知，不同的置信水平对应于不同的系统总成本。例如，当α为0、0.2、0.5、0.8和1时，系统总成本分别为［340.8，481.0］×105，［341.9，477.1］×105，［343.6，471.3］× 105，［345.4，465.6］×105和［346.5，461.8］×105元。一般而言，置信水平的变化将引起污染物单位处理成本、污染物超标排放单位成本、污染物排放速率限值和污染物地面浓度限值的变化，进而导致系统总成本的变化。在一定的置信水平下，对于系统总成本而言，它的区间值下界对应于污染物处理与超标排放单位成本的区间值下界以及污染物排放速率与地面浓度限值的区间值上界；相反的，它的区间值上界对应于污染物处理与超标排放单位成本的区间值上界以及污染物排放速率与地面浓度限值的区间值下界。同时，随着置信水平的增大，对于污染物处理与超标排放单位成本以及污染物排放速率与地面浓度限值而言，它们的区间值下界均增大，而区间值上界均减小。因此，随着置信水平的增大，系统总成本的区间值下界逐渐增大，而它的区间值上界逐渐减小，系统总成本的区间距离逐渐减小，分别为140.2×105元（α=0），135.2×105元（α=0.2），127.7×105元（α= 0.5），120.2×105元（α=0.8）和115.3×105元（α=1）。系统总成本的变化趋势说明当置信水平增大时，系统稳定性增强。

表4列出了生产企业在不同污染物产生概率水平下利用不同控制措施处理污染物的量（α=1）。

图2　不同置信水平下的系统总成本Fig.2Total system costs under different confidence levels

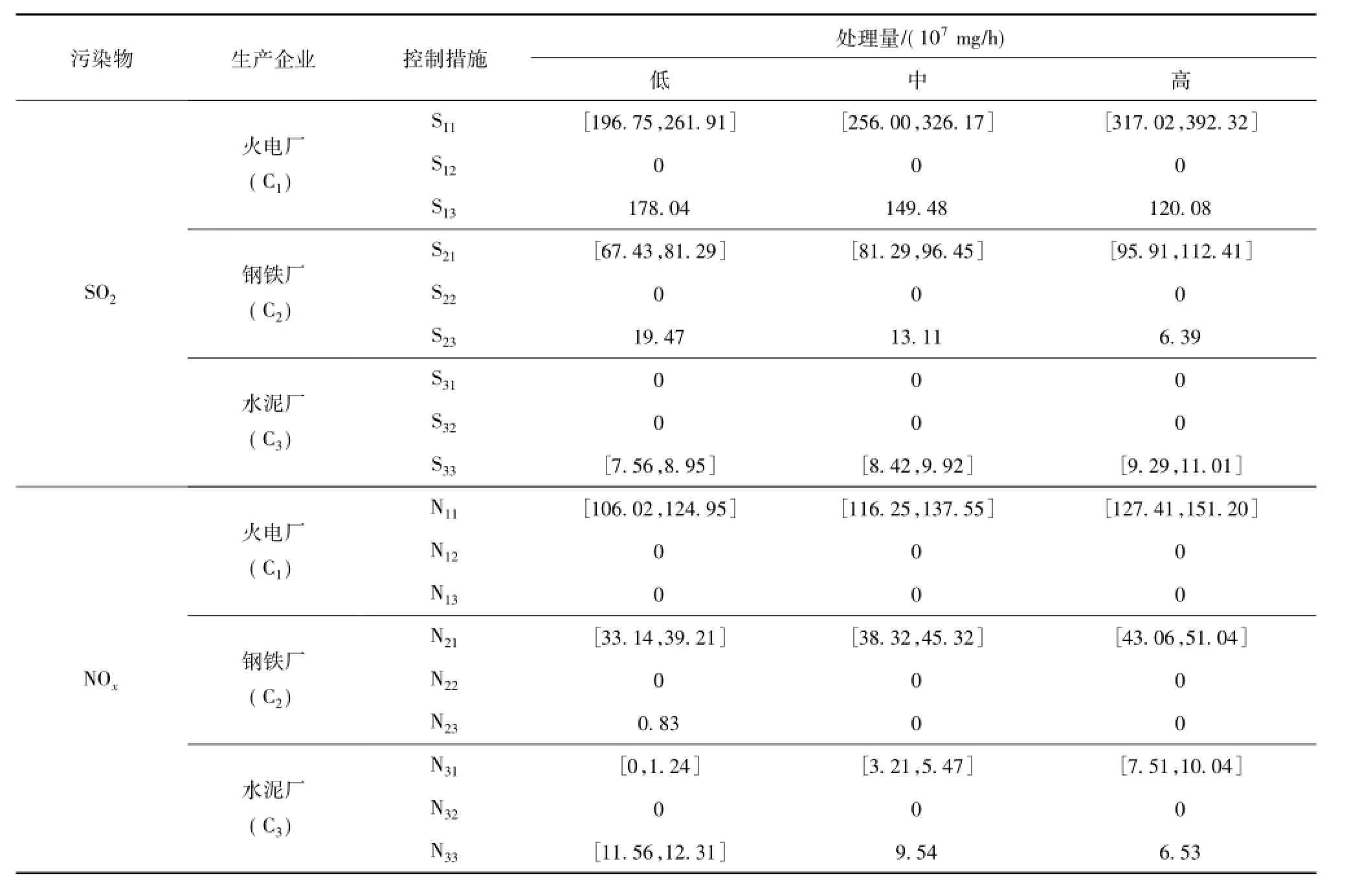
表4　生产企业在不同污染物产生概率水平下利用控制措施处理污染物的量（α=1）Table 4Treatment amounts of pollutants using control measures under different probability levels of pollutants generation for production enterprises（α=1）

不同污染物控制措施的处理效率及单位处理成本是不同的，因此，为了控制污染物的排放和满足敏感区的环境空气质量标准，以及兼顾污染物的处理成本，生产企业能够确定合适的污染物控制措施和处理量。例如，在低污染物产生概率水平时，火电厂采用措施S11和S13处理SO2，处理量分别为［196.75，261.91］×107和178.04×107mg/h；仅采用措施N11处理NOx，处理量为［106.02，124.95］× 107mg/h。在低污染物产生概率水平时，钢铁厂采用措施S21和S23处理SO2，措施S21的处理量（［67.43，81.29］×107mg/h）数倍于措施S23的处理量（19.47×107mg/h）；采用措施N21和N23处理NOx，措施N21的处理量（［33.14，39.21］×107mg/h）远大于措施N23的处理量（0.83×107mg/h）。在低污染物产生概率水平时，水泥厂仅采用措施S33处理SO2，处理量为［7.56，8.95］×107mg/h；采用措施N31和N33处理NOx，处理量分别为［0，1.24］×107和［11.56，12.31］×107mg/h。当污染物产生概率水平为中等水平或高水平时，生产企业采用具有较高污染物处理效率的控制措施去处理污染物的量会增加。例如，在污染物产生概率水平为中等水平和高水平时，火电厂均采用措施S11和S13处理SO2，处理量分别为［256.00，326.17］×107和149.48×107mg/h，［317.02，392.32］×107和120.08×107mg/h；水泥厂均采用措施N31和N33处理NOx，处理量分别为［3.21，5.47］×107和9.54×107mg/h，［7.51，10.04］×107和6.53×107mg/h。一般而言，为了控制污染物处理成本，生产企业尽可能选择具有较低污染物单位处理成本的控制措施，但为了控制污染物的排放以及满足敏感区的环境空气质量标准，生产企业应该选择具有较高污染物处理效率的控制措施。对于控制措施而言，较高的处理效率将关联较高的处理成本，因此，决策者需要在污染物处理效率与处理成本之间做出合理的权衡。

图3描述了水泥厂在不同置信水平和中等NOx产生概率水平下的NOx处理量。不同的置信水平关联不同的NOx处理量。随着置信水平的增大，水泥厂采用措施N31处理NOx的量逐渐减少，采用措施N33处理NOx的量逐渐增加。在中等NOx产生概率水平下，当α为0、0.2、0.5、0.8和1时，水泥厂采用措施N31处理NOx的量分别为［5.02，7.28］× 107，［4.66，6.92］×107，［4.12，6.38］×107，［3.57，5.83］×107和［3.21，5.47］×107mg/h；采用措施N33处理NOx的量分别为7.72×107，8.08×107，8.63×107，9.17×107和9.54×107mg/h。在任意污染物产生概率水平下，不同生产企业的污染物处理量在不同置信水平下具有相似的变化趋势。随着置信水平的增大，污染物排放速率限值和地面浓度限值的区间值下界均增大，而它们的区间值上界均减小。同时，基于控制措施的处理效率和单位处理成本，在一定范围内，可以减少具有较高处理效率的控制措施的处理量，而增加具有较低处理效率的控制措施的处理量，从而既控制污染物的排放和满足敏感区环境空气质量标准，又实现系统总成本的最小化。

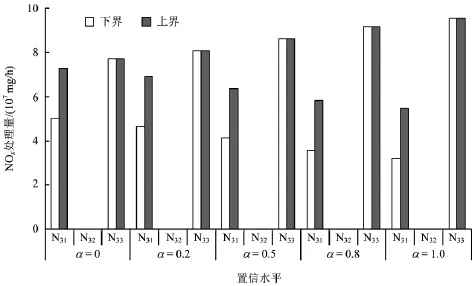
图3　水泥厂在不同置信水平和中等NOx产生概率水平下的NOx处理量Fig.3Treatment amounts of NOxunder different confidence levels and medium probability level of NOxgeneration for cement plant

表5列出了火电厂和钢铁厂在不同置信水平下的NOx超标排放量。然而，在不同置信水平下，生产企业的SO2超标排放量和水泥厂的NOx超标排放量均为0。为了满足敏感区环境空气质量标准，以及最大限度地控制污染物排放以降低污染物超标排放费用，生产企业利用控制措施进行污染物的处理。但是，控制措施的处理效率是有限的，污染物超标排放时有发生。例如，当α为0.5时，在低NOx产生概率水平下，火电厂和钢铁厂的NOx超标排放量分别为［0，4.24］×107和［0，0.16］×107mg/h。同时，污染物产生量增大，污染物超标排放量可能增大。例如，当α为1时，在NOx产生概率水平为低、中和高水平下，火电厂的NOx超标排放量分别为［0，3.74］×107、［0，6.13］×107和［0，8.73］×107mg/h；钢铁厂的NOx超标排放量分别为0、［0，1.12］× 107和［0，2.44］×107mg/h。不同的置信水平影响污染物的超标排放量。在相同的污染物产生概率水平下，随着置信水平的增大，污染物超标排放量的区间值上界可能减小。例如，在高NOx产生概率水平下，当α为0、0.2、0.5、0.8和1时，火电厂的NOx超标排放量分别为［0，9.73］×107，［0，9.53］×107，［0，9.23］×107，［0，8.93］×107和［0，8.73］×107mg/h。这是因为对于污染物排放速率限值和地面浓度限值而言，随着置信水平的增大，它们的区间值下界均增大，而它们的区间值上界均减小。同时，它们的区间值下界关联污染物超标排放量的区间值上界，而它们的区间值上界关联污染物超标排放量的区间值下界。

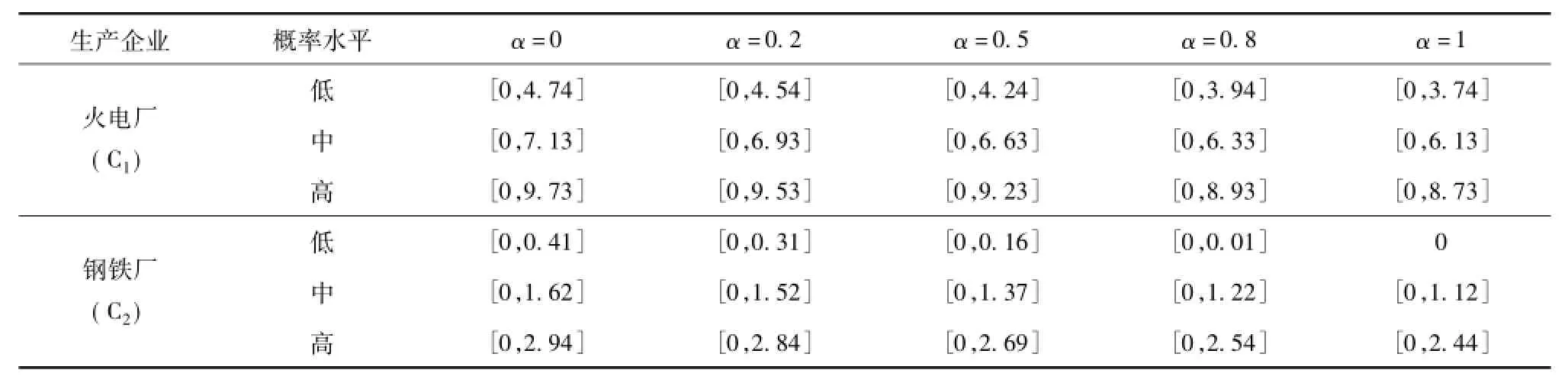
表5　火电厂和钢铁厂在不同置信水平下的NOx超标排放量Table 5Excess emission amounts of NOxunder different confidence levels for power plant and steel plant107mg/h

3　结论

在研究中，基于ILP、SMP和FPP 3种不确定性优化方法，开发了ISFPP模型，应用于空气质量管理问题。在空气质量管理系统中，ISFPP模型不仅能够处理表示为离散区间数、概率密度函数和模糊隶属函数的多重不确定性，而且能够反映系统的复杂性。同时，ISFPP模型能够分析不同置信水平下的管理情景。模型结果是确定性的、区间的及分布信息的组合，能够实现空气质量管理的多种决策选择。

开发的ISFPP模型应用到某个假设的空气质量管理案例中。不同置信水平下的模型结果被分析，表明置信水平的变化，将导致系统总成本、污染物处理量及超标排放量发生相应的变化。同时，基于模型结果，生产企业能够实现污染物控制措施的选择以及污染物处理量和超标排放量的确定，最终生成不同情景的管理决策。

开发的ISFPP模型整合了不同的优化方法，模型与方法是简单和有效的管理工具。同时，其他的不确定性优化方法（例如，两阶段随机规划、机会约束规划和模糊鲁棒规划）能够被整合进ISFPP模型中去处理各种类型的不确定性，以实现最小的系统总成本和强化问题的决策支持。

［1］辛志玲，张金龙，张大全，等.高效液相吸收剂同时脱硫脱硝的实验研究［J］.中国电机工程学报，2009，29（17）：76-82.

［2］EKINCI E.Dispersion modeling：a tool for local air quality management［J］.International Journal of Environment and Pollution，1998，10（2）：254-260.

［3］FEDRA K，HAURIE A.A decision support system for air quality management combining GIS and optimization techniques［J］. International Journal of Environment and Pollution，1999，12（2/ 3）：125-146.

［4］LIU L，HUANG G H，LIU Y，et al.A fuzzy-stochastic robust programming model for regional air quality management under uncertainty［J］.Engineering Optimization，2003，35（2）：177-199.

［5］LI Y P，HUANG G H，VEAWAB A，et al.Two-stage fuzzystochastic robust programming：a hybrid model for regional air quality managemen［J］.JournaloftheAirandWaste Management Association，2006，56（8）：1070-1082.

［6］LU H W，HUANG G H，LIU L，et al.An interval-parameter fuzzystochastic programming approach for air quality management under uncertainty［J］.Environmental Engineering Science，2008，25（6）：895-909.

［7］OLIVEIRA C，ANTUNES C H.A multi-objective multi-sectoral economy-energy-environment model：application to Portugal［J］. Energy，2011，36（5）：2856-2866.

［8］LYU Y，HUANG G H，LI Y P，et al.A two-stage inexact jointprobabilistic programming method for air quality management under uncertainty［J］.Journal of Environmental Management，2011，292（3）：813-826.

［9］XU Y，SHAO L G，HUANG G H.An inexact fuzzy-randomchance-constrained air quality management model［J］.Stochastic Environmental Research and Risk Assessment，2013，27（8）：1929-1946.

［10］CHEN W T，LI Y P，HUANG G H，et al.A two-stage inexactstochasticprogrammingmodelforplanningcarbondioxide emission trading under uncertainty［J］.Applied Energy，2010，87（3）：1033-1047.

［11］WATANABE T，ELLIS H.Stochastic-programming models for airquality management［J］.Computers and Operations Research，1993，20（6）：651-663.

［12］MA X M，ZHANG F.A genetic algorithm based on stochastic programming model for air quality management［J］.Journal of Environmental Science：China，2002，14（3）：367-374.

［13］QIN X S，HUANG G H，LIU L.A genetic-algorithm-aided stochastic optimization model for regional air quality management under uncertainty［J］.Journal of the Air and Waste Management Association，2010，60（1）：63-71.

［14］XU Y，HUANG G H，QIN X S.An inexact fuzzy-chanceconstrained air quality management model［J］.Journal of the Air and Waste Management Association，2010，60（7）：805-819.

［15］WANG X W，CAI Y P，CHEN J J，et al.A grey-forecasting interval-parametermixed-integerprogrammingapproachfor integrated electric-environmental management：a case study of Beijing［J］.Energy，2013（63）：334-344.

［16］WANG S，HUANG G H.A coupled factorial-analysis-based interval programming approach and its application to air quality management［J］.Journal of the Air and Waste Management Association，2013，63（2）：179-189.

［17］胡情，黄国和，李薇，等.基于模糊可行性分析的发电侧节能减排规划［J］.现代电力，2013，30（2）：83-88.

［18］蒋展鹏.环境工程学［M］.2版.北京：高等教育出版社，2005：477-490.

［19］国家技术监督局.GB/T 3840—91制定地方大气污染物排放标准的技术方法［S］.北京：中国标准出版社，1991.

［20］HUANG G H.IPWM：an interval parameter water quality management model［J］.Engineering Optimization，1996，26（2）：79-103.

［21］LIYP，HUANGGH.Aninterval-basedpossibilistic programming method for waste management with cost minimization and environmental-impact abatement under uncertainty［J］. Science of the Total Environment，2010，408（20）：4296-4308.

［22］LAI Y J，HWANG C L.Fuzzy mathematical programming：methods and applications［M］.New York：Springer-Verlag Berlin and Heidelberg GmbH&Co.，1992.

［23］FAN Y R，HUANG G H.A robust two-step method for solving interval linear programming problems within an environmental management context［J］.Journal of Environmental Informatics，2012，19（1）：1-9.□

Air Quality Management Based on An Inexact Optimization Model

LIU Min，ZHENG Chuan-jiang，LU Hai-qing
Electric Power Research Institute of State Grid Zhejiang Electric Power Company，Hangzhou 310014，China

In air quality management systems，aiming at the existence of multiple uncertainties and system complexities，based on the methods of interval linear programming（ILP），stochastic mathematical programming（SMP）and fuzzy possibilistic programming（FPP），an interval stochastic fuzzy possibilistic programming（ISFPP）model was developed to identify effective management policies.The developed ISFPP model can not only deal with multiple uncertainties，but also reflect system complexities.Moreover，the ISFPP model can help to analyze various management scenarios associated with different confidence levels.The ISFPP model was applied to a hypothetical case study of air quality management.The results indicate that the change of confidence level may lead to the corresponding changes of total system cost，treatment amounts of pollutants and emission amounts exceeding the standards；moreover，under different confidence levels，different enterprises can select the appropriate pollutant control measures and determine the reasonable treatment amounts of pollutants and emission amounts exceeding the standards.Thus，the modeling results can be used for generating decision alternatives，and help the decisionmakers to identify desired management policies.

air quality management；optimization model；interval linear programming；stochastic mathematical programming；fuzzy possibilistic programming；uncertainty

X321

1674-991X（2015）02-0097-09doi：10.3969/j.issn.1674-991X.2015.02.015

2014-11-20

刘敏（1986—），男，助理工程师，硕士，主要从事电厂环保工作，liumin-224@163.com