波导传感器中高效柱面波平面波转换结构的变换光学设计

2015-08-24颜森林孙小菡

传感技术学报 2015年12期

关键词：平面波波导电磁波

曹　军，颜森林，孙小菡

（1.南京晓庄学院电子工程学院，南京211171；2.东南大学电子科学与工程学院，南京210096）

波导传感器中高效柱面波平面波转换结构的变换光学设计

曹军1*，颜森林1，孙小菡2

（1.南京晓庄学院电子工程学院，南京211171；2.东南大学电子科学与工程学院，南京210096）

基于阻抗可调的变换光学理论，设计了波导传感器中二维平面波和柱面波相互转换的光学结构。通过在虚拟空间设置合适的阻抗函数，变换介质边界上的反射得到有效消除，实现了高效的平面波到柱面波转换；转换效率将随着输入波束宽度的增加而提高。四个相似转换结构的组合，可实现高效柱面波-平面波转换，与采用传统的变换光学设计比较，基于阻抗可调变换光学理论的设计，数值模拟表明转换效率可提高约百分之六。

柱面波平面波转换；波导传感器；阻抗可调；变换光学

EEACC：4110；4130doi：10.3969/j.issn.1004-1699.2015.12.005

柱面波与平面波相互转换是波导传感器［1-2］中非常重要的结构单元，如何得到高效的转换效率一直是急需解决的问题。而基于麦克斯韦方程组协变的变换光学理论提供了一种全新的控制电磁波传播方法［3］，通过选择合适的坐标变换可以设计各种具有独特功能的电磁波器件，如隐形［4］，波导弯曲［5-6］，旋转器［7-8］，能量聚集器［9-10］等。嵌入式坐标变换理论［11］加快了变换光学设计的步伐，以更加灵活的方式可设计各种具有独特功能的电磁波器件，但是嵌入式坐标变换是不连续的坐标变换，当理论应用于某些变换光学设计［12-14］时，由于电场方向和磁场方向的坐标拉伸率不同，导致在边界阻抗失配，存在反射，影响了器件的性能。应用阻抗可调的变换光学理论［15］，在虚拟空间预先设置空间连续的阻抗函数，可以抵消不连续坐标变换带来的阻抗失配，从而消除边界上的反射，阻抗可调变换光学理论推广了变换光学理论，由于阻抗函数的非唯一性，变换介质的材料参数可以有多种选择，便于实验实现。

应用变换光学理论可以同时控制电磁波传播方向和强度，柱面波与平面波转换结构就是其中的一个典型的例子，通过坐标变换把虚拟空间中的一条弧线变换到物理空间中的直线，而这种弧线和直线的坐标变换必然会导致变换介质边界上的阻抗失配［13］，通过数值模拟证实了边界上有少量的反射存在［14］。本文应用阻抗可调变换光学理论［15］通过在虚拟设置合适的阻抗函数方法消除反射，实现高效的平面波与柱面波转换，该结构可方便应用于波导传感器中的电磁波转换单元。

1　柱面波平面波转换器设计

在阻抗可调变换光学设计中，设置虚拟空间中的介电常数和磁导率分别为ε0/k和kμ0，对于给定的变换为雅可比变换矩阵的矩阵元，变换介质的介电常数和磁导率可由下式［15］计算得到：

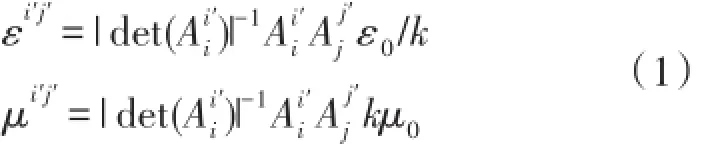
本文的主要工作是在柱面波平面波转换器的变换光学设计中找到一个合适的阻抗函数k，消除边界反射，提高转换效率。

1.1坐标变换

柱面波平面波转换装置二维坐标变换如图1所示，把虚拟空间中内外半径分别为r1，r2的弧形区域（x,y,z）变换到变换空间中的四边形区域ABCD（x′,y′,z′）。

图1　R柱面波平面波转换结构坐标变换示意图

设坐标变换沿半径方向线性，则坐标变换公式为：

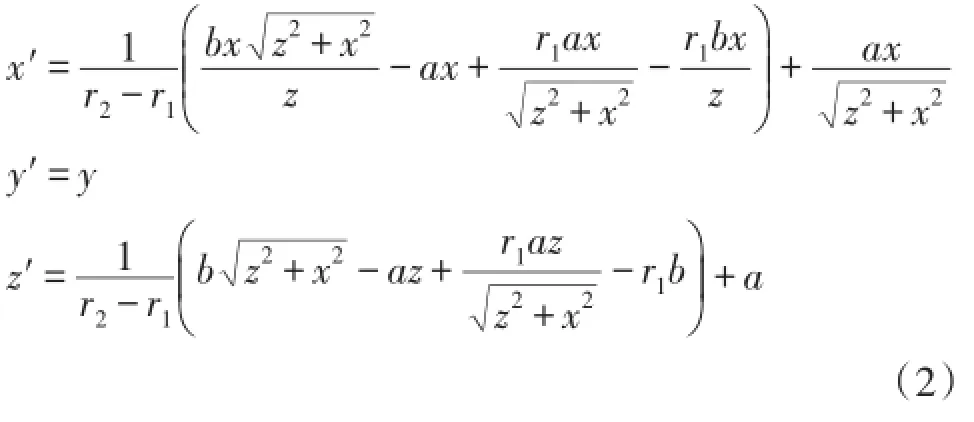
上述变换矩阵的矩阵元为：

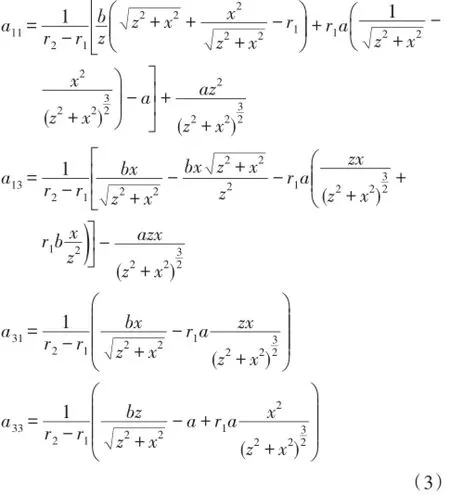
其它的矩阵元都为0，上述的表达式都要统一转换成变换空间的坐标。

1.2阻抗函数

若选择参数r1=a，上述的变换在弧线边界AB上连续，而在直线边界CD上不连续，通过考察边界CD上的反射系数设置阻抗函数，这里只讨论TE平面极化波入射情况，设电磁波沿与z轴成θ角从边界AB上E点入射到变换介质，从边界CD上F点垂直射出。根据几何光学理论，由电磁场的切向连续性条件得到反射系数为：

用传统的变换光学设计（k=1），在角度不太大的情况下，上述的反射系数约等于零，可认为阻抗近似匹配。而随着角度的增大，失配的程度越大，这时采用阻抗匹配技术是必要的，通过设置阻抗函数可以消除反射，提高转换效率。

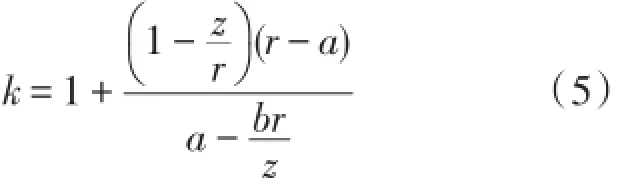
1.3数值模拟与分析

应用有限元计算软件Comsol对上述设计的柱面波平面波转换结构进行数值模拟，参数取r1=a=0.2m，b=0.4m，r2=0.3m，AD与BC的夹角为120°，首先模拟平面波到柱面波转换，采用高斯波模拟平面波，设输入高斯波电场强度的表达式为exp（-x2/h），从右向左正中间入射边界CD，波束的宽度由参数h决定，取h=0.6m2，输入波的频率为6 GHz，满足几何光学近似条件。如图2（a），当采用传统的变换光学设计（阻抗不可调k=1）时，边界有少量的反射存在，转换效率约95%（定义转换效率为转换装置输出端的功率与输入端的功率比值）；用阻抗可调变换光学设计设置合适的阻抗函数（由式（5）确定）后，如图2（b）所示，消除了反射，转换效率接近100%，与图2（a）相比，平面波到柱面波的转换效率提高了约5%。

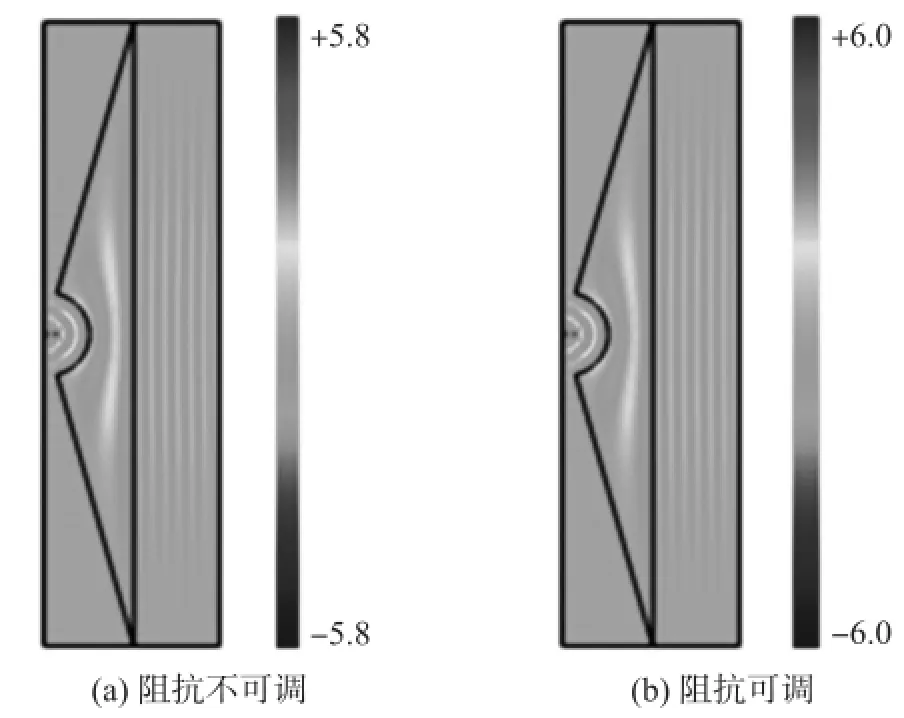
图2　R平面波到柱面波转换结构中电场分布

由前面的理论分析可知，当电磁波波束的宽度很小时，电磁波能量主要集中在中间，这时候采用传统的变换光学方法设计（k=1）阻抗失配不大，反射微小，可以忽略，而随着入射波的宽度增大，反射增强。采用阻抗可调变换光学设计提高的效率与入射波的宽度有关，如图3所示，随着输入波波束宽度的增加，采用阻抗可调变换光学设计与传统变换光学设计比较，提升的平面波到柱面波转换效率增加，体现了采用阻抗匹配技术的必要性。

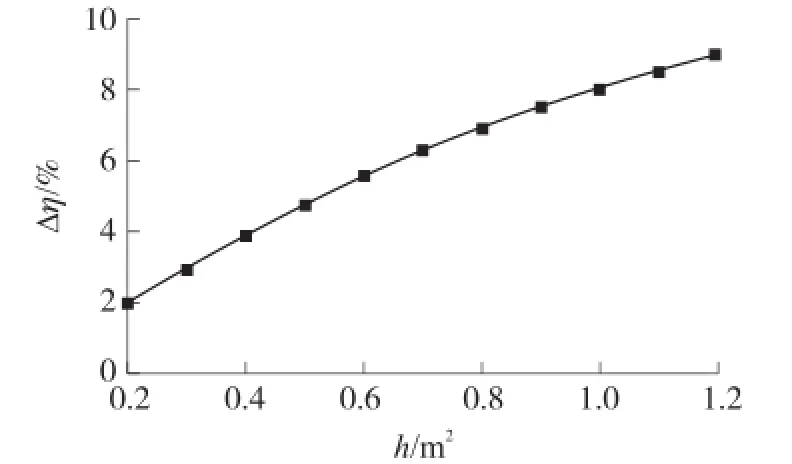
图3　R不同宽度波束入射下采用阻抗匹配对提高转换效率的影响

由于光路的可逆性，若在焦点O处输入点源，该装置可实现柱面波到平面波的转换。利用多个这样相似的结构可实现多路定向柱面波到平面波的转换，文献［14］中，设计了四路柱面波到平面波的转换结构，由于在变换介质的外边界阻抗失配，数值模拟中观察到了少量的反射，如图4（a），与我们的理论分析一致。通过设置合适的阻抗函数，可以消除外边界的反射，模拟结构如图4（b）。由于图4（a）中反射不大，因而图4（a）与4（b）中模场分布差别很小，只是幅度略有不同，但通过出射效率的计算，采用阻抗可调的变换光学设计后转换的效率提升了约6%。

最后我们通过数值模拟计算了不同频率下采用阻抗可调变换光学设计与传统变换光学设计时的效率，并进行比较，如图5所示，通过设置合适的阻抗函数后提升的柱面波到平面波转换效率在不同的入射波频率下都能维持在6%左右。

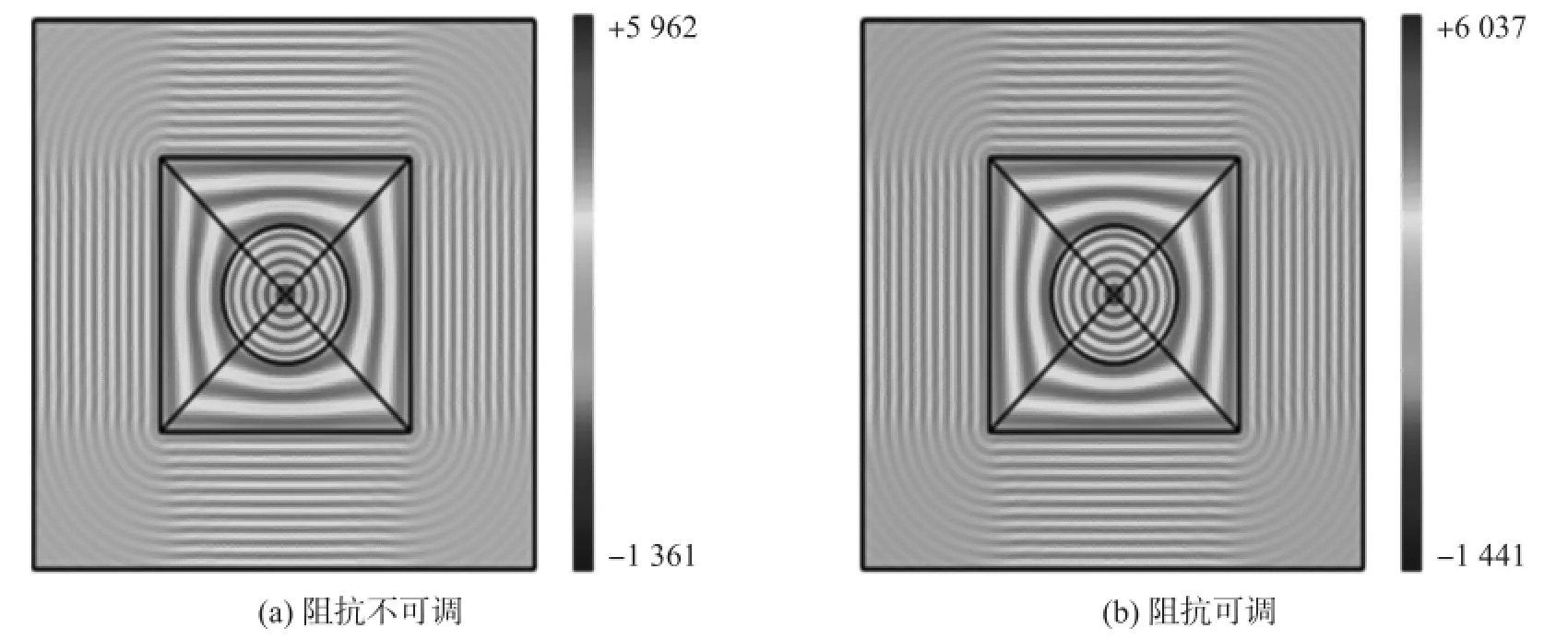
图4　R柱面波到平面波转换结构中电场分布

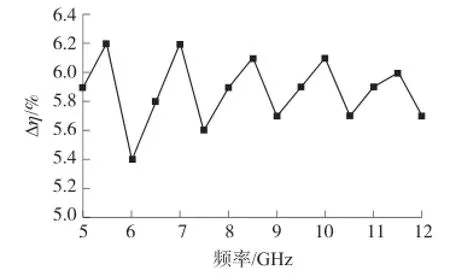
图5　R不同频率下设置阻抗函数对柱面波到平面波转换效率的提升

2　结论

采用阻抗可调变换光学理论，设计了一种可应用于波导传感的高效二维平面波柱面波转换结构单元。通过考察边界上的反射系数，推导了虚拟空间中的阻抗函数，数值模拟表明采用阻抗可调变换光学设计消除了反射，提高了柱面波平面波转换效率，该方法可推广应用于三维变换光学设计。

［1］张毅，庄志，陈颖.基于光子晶体光纤的在线压力监测技术［J］.传感技术学报，2015，28（5）：613-616.

［2］李鹏，张宇光，王丽等，闫树斌.一种基于SOI的集成光波导耦合系统的设计与制备［J］.传感技术学报，2011，24（6）：839-842.

［3］Pendry J B，Schurig D，Smith D R.Controlling Electromagnetic Fields［J］.Science，2006，312：1780-1782.

［4］Schurig D，Mock J J，Justice B J，et al.Metamaterial Electromagnetic Cloak at Microwave Frequencies［J］.Science，2006，314： 977-980.

［5］Huangfu J，Xi S，Kong F，et al.Application of Coordinate Transformation in Bent Waveguides［J］.J Appl Phys，2008，104：014502.

［6］Roberts D A，Rahm M，Pendry J B，et al.Transformation-Optical Design of Sharp Waveguide Bends and Corners［J］.Appl Phys Lett，2008，93：251111.

［7］Chen H，Chan C T.Transformation Media That Rotate Electromagnetic Fields［J］.Appl Phys Lett，2007，90：241105.

［8］代黎明，廖成，周海京，等.任意形状隐身斗篷和电磁旋转器的研究［J］.微波学报，2011，27（2）：93-96.

［9］Rahm M，Schurig D，Roberts D A，et al.Design of Electromagnetic Cloaks and Concentrators Using Form-Invariant Coordinate Transformations of Maxwell's Equations［J］.Photonics Nanostruct Fundam Appl，2008，6：87-92.

［10］杨成福，杨晶晶，黄铭，等.基于超材料的椭圆形电磁波聚集器设计［J］.光子学报，2010，39（7）：1203-1207.

［11］Rahm M，Cummer S A，Schurig D，et al.Optical Design of Reflectionless Complex Media by Finite Embedded Coordinate Transformations［J］.Phys Rev Lett，2008，100：063903.

［12］Rahm M，Roberts D A，Pendry J B，et al.Transformation-Optical Design of Adaptive Beam Bends and Beam Expanders［J］.Opt Express，2008，16：11555-11567.

［13］Kwon D H，Werner D H.Flat Focusing Lens Designs Having Minimized Reflection Based on Coordinate Transformation Techniques［J］.Opt Express，2009，17：7807-7817.

［14］Jiang W X，Cui T J，Ma H F，et al.Cylindrical-to-Plane-Wave Conversion via Embedded Optical Transformation［J］.Appl Phys Lett，2008，96：261903.

［15］Cao J，Zhang L F，Yan S L，et al.Reflectionless Design of Optical Elements Using Impedance-Tunable Transformation Optics［J］. Appl Phys Lett，2014，104：191102.

Transformation Optical Design of High Efficiency Cylindrical-to-Plane-Wave Conversion in Waveguide Sensor

CAO Jun1*，YAN Senlin1，SUN Xiaohan2
（1.Department of Electronic Engineering，Nanjing Xiaozhuang University，Nanjing 211171，China 2.Department of Electronic Engineering，Southeast University，Nanjing 210096，China）

Based on impedance-tunable transformation optics，the optical design of two dimensional conversion between cylindrical waves and plane waves is realized in waveguide sensor.By tuning impedance coefficients in the original space to remove the reflections at the boundary，a high efficient plane-to-cylindrical-wave conversion is obtained through calculating the reflection coefficient of the waves at the boundary；the efficiency can be enhanced with increasing the beam width.Four similar structures are designed for a high-efficiency cylindrical-to-plane-wave conversion，one can obtain a higher efficiency by using impedance-tunable transformation optics compared with conventional transformation optics，and the numerical simulations show that increased efficiency is about six percent.

Cylindrical-to-plane-wave conversion；waveguide sensor；impedance tunable；transformation optics